Tidymodels Workflow with Sequential Keras Models

Introduction

This vignette demonstrates a complete tidymodels workflow for a classification task using a Keras sequential model defined with kerasnip. We will use the Palmer Penguins dataset to predict penguin species based on physical measurements.

The kerasnip package allows you to define Keras models using a modular “layer block” approach, which then integrates seamlessly with the parsnip and tune packages for model specification and hyperparameter tuning.

Setup

First, we load the necessary packages.

library(kerasnip)
library(tidymodels)
#> ── Attaching packages ────────────────────────────────────── tidymodels 1.3.0 ──
#> ✔ broom        1.0.9     ✔ recipes      1.3.1
#> ✔ dials        1.4.1     ✔ rsample      1.3.1
#> ✔ dplyr        1.1.4     ✔ tibble       3.3.0
#> ✔ ggplot2      3.5.2     ✔ tidyr        1.3.1
#> ✔ infer        1.0.9     ✔ tune         1.3.0
#> ✔ modeldata    1.5.1     ✔ workflows    1.2.0
#> ✔ parsnip      1.3.2     ✔ workflowsets 1.1.1
#> ✔ purrr        1.1.0     ✔ yardstick    1.3.2
#> ── Conflicts ───────────────────────────────────────── tidymodels_conflicts() ──
#> ✖ purrr::discard() masks scales::discard()
#> ✖ dplyr::filter()  masks stats::filter()
#> ✖ dplyr::lag()     masks stats::lag()
#> ✖ recipes::step()  masks stats::step()
library(keras3)
#> 
#> Attaching package: 'keras3'
#> The following object is masked from 'package:yardstick':
#> 
#>     get_weights
library(dplyr)          # For data manipulation
library(ggplot2)        # For plotting
library(future)         # For parallel processing
#> 
#> Attaching package: 'future'
#> The following object is masked from 'package:keras3':
#> 
#>     %<-%
library(finetune)       # For racing

Data Preparation

We’ll use the penguins dataset from the modeldata package. We will clean it by removing rows with missing values and ensuring the species column is a factor.

# Remove rows with missing values
penguins_df <- penguins |>
  na.omit() |>
  # Convert species to factor for classification
  mutate(species = factor(species))

# Split data into training and testing sets
set.seed(123)
penguin_split <- initial_split(penguins_df, prop = 0.8, strata = species)
penguin_train <- training(penguin_split)

penguin_test <- testing(penguin_split)

# Create cross-validation folds for tuning
penguin_folds <- vfold_cv(penguin_train, v = 5, strata = species)

Recipe for Preprocessing

We will create a recipes object to preprocess our data. This recipe will: * Predict species using all other variables. * Normalize all numeric predictors. * Create dummy variables for all categorical predictors.

penguin_recipe <- recipe(species ~ ., data = penguin_train) |>
  step_normalize(all_numeric_predictors()) |>
  step_dummy(all_nominal_predictors())

Define Keras Sequential Model with kerasnip

Now, we define our Keras sequential model using kerasnip’s layer blocks. We’ll create a simple Multi-Layer Perceptron (MLP) with two hidden layers.

For a sequential Keras model with tabular data, all preprocessed input features are typically combined into a single input layer. The recipes package handles this preprocessing, transforming predictors into a single matrix that serves as the input to the Keras model.

# Define layer blocks
input_block <- function(model, input_shape) {
  keras_model_sequential(input_shape = input_shape)
}

hidden_block <- function(model, units = 32, activation = "relu", rate = 0.2) {
  model |>
    layer_dense(units = units, activation = activation) |>
    layer_dropout(rate = rate)
}

output_block <- function(model, num_classes, activation = "softmax") {
  model |>
    layer_dense(units = num_classes, activation = activation)
}

# Create the kerasnip model specification function
create_keras_sequential_spec(
  model_name = "penguin_mlp",
  layer_blocks = list(
    input = input_block,
    hidden_1 = hidden_block,
    hidden_2 = hidden_block,
    output = output_block
  ),
  mode = "classification"
)

Model Specification

We’ll define our penguin_mlp model specification and set some hyperparameters to tune(), indicating that they should be optimized. We will also set fixed parameters for compilation and fitting.

# Define the tunable model specification
mlp_spec <- penguin_mlp(
  # Tunable parameters for hidden layers
  hidden_1_units = tune(),
  hidden_1_rate = tune(),
  hidden_2_units = tune(),
  hidden_2_rate = tune(),
  # Fixed compilation and fitting parameters
  compile_loss = "categorical_crossentropy",
  compile_optimizer = "adam",
  compile_metrics = c("accuracy"),
  fit_epochs = 20,
  fit_batch_size = 32,
  fit_validation_split = 0.2,
  fit_callbacks = list(
    callback_early_stopping(monitor = "val_loss", patience = 5)
  )
) |>
  set_engine("keras")

print(mlp_spec)
#> penguin mlp Model Specification (classification)
#> 
#> Main Arguments:
#>   num_input = structure(list(), class = "rlang_zap")
#>   num_hidden_1 = structure(list(), class = "rlang_zap")
#>   num_hidden_2 = structure(list(), class = "rlang_zap")
#>   num_output = structure(list(), class = "rlang_zap")
#>   hidden_1_units = tune()
#>   hidden_1_activation = structure(list(), class = "rlang_zap")
#>   hidden_1_rate = tune()
#>   hidden_2_units = tune()
#>   hidden_2_activation = structure(list(), class = "rlang_zap")
#>   hidden_2_rate = tune()
#>   output_activation = structure(list(), class = "rlang_zap")
#>   learn_rate = structure(list(), class = "rlang_zap")
#>   fit_batch_size = 32
#>   fit_epochs = 20
#>   fit_callbacks = list(callback_early_stopping(monitor = "val_loss", patience = 5))
#>   fit_validation_split = 0.2
#>   fit_validation_data = structure(list(), class = "rlang_zap")
#>   fit_shuffle = structure(list(), class = "rlang_zap")
#>   fit_class_weight = structure(list(), class = "rlang_zap")
#>   fit_sample_weight = structure(list(), class = "rlang_zap")
#>   fit_initial_epoch = structure(list(), class = "rlang_zap")
#>   fit_steps_per_epoch = structure(list(), class = "rlang_zap")
#>   fit_validation_steps = structure(list(), class = "rlang_zap")
#>   fit_validation_batch_size = structure(list(), class = "rlang_zap")
#>   fit_validation_freq = structure(list(), class = "rlang_zap")
#>   fit_verbose = structure(list(), class = "rlang_zap")
#>   fit_view_metrics = structure(list(), class = "rlang_zap")
#>   compile_optimizer = adam
#>   compile_loss = categorical_crossentropy
#>   compile_metrics = c("accuracy")
#>   compile_loss_weights = structure(list(), class = "rlang_zap")
#>   compile_weighted_metrics = structure(list(), class = "rlang_zap")
#>   compile_run_eagerly = structure(list(), class = "rlang_zap")
#>   compile_steps_per_execution = structure(list(), class = "rlang_zap")
#>   compile_jit_compile = structure(list(), class = "rlang_zap")
#>   compile_auto_scale_loss = structure(list(), class = "rlang_zap")
#> 
#> Computational engine: keras

Create Workflow

A workflow combines the recipe and the model specification.

penguin_wf <- workflow() |>
  add_recipe(penguin_recipe) |>
  add_model(mlp_spec)

print(penguin_wf)
#> ══ Workflow ════════════════════════════════════════════════════════════════════
#> Preprocessor: Recipe
#> Model: penguin_mlp()
#> 
#> ── Preprocessor ────────────────────────────────────────────────────────────────
#> 2 Recipe Steps
#> 
#> • step_normalize()
#> • step_dummy()
#> 
#> ── Model ───────────────────────────────────────────────────────────────────────
#> penguin mlp Model Specification (classification)
#> 
#> Main Arguments:
#>   num_input = structure(list(), class = "rlang_zap")
#>   num_hidden_1 = structure(list(), class = "rlang_zap")
#>   num_hidden_2 = structure(list(), class = "rlang_zap")
#>   num_output = structure(list(), class = "rlang_zap")
#>   hidden_1_units = tune()
#>   hidden_1_activation = structure(list(), class = "rlang_zap")
#>   hidden_1_rate = tune()
#>   hidden_2_units = tune()
#>   hidden_2_activation = structure(list(), class = "rlang_zap")
#>   hidden_2_rate = tune()
#>   output_activation = structure(list(), class = "rlang_zap")
#>   learn_rate = structure(list(), class = "rlang_zap")
#>   fit_batch_size = 32
#>   fit_epochs = 20
#>   fit_callbacks = list(callback_early_stopping(monitor = "val_loss", patience = 5))
#>   fit_validation_split = 0.2
#>   fit_validation_data = structure(list(), class = "rlang_zap")
#>   fit_shuffle = structure(list(), class = "rlang_zap")
#>   fit_class_weight = structure(list(), class = "rlang_zap")
#>   fit_sample_weight = structure(list(), class = "rlang_zap")
#>   fit_initial_epoch = structure(list(), class = "rlang_zap")
#>   fit_steps_per_epoch = structure(list(), class = "rlang_zap")
#>   fit_validation_steps = structure(list(), class = "rlang_zap")
#>   fit_validation_batch_size = structure(list(), class = "rlang_zap")
#>   fit_validation_freq = structure(list(), class = "rlang_zap")
#>   fit_verbose = structure(list(), class = "rlang_zap")
#>   fit_view_metrics = structure(list(), class = "rlang_zap")
#>   compile_optimizer = adam
#>   compile_loss = categorical_crossentropy
#>   compile_metrics = c("accuracy")
#>   compile_loss_weights = structure(list(), class = "rlang_zap")
#>   compile_weighted_metrics = structure(list(), class = "rlang_zap")
#>   compile_run_eagerly = structure(list(), class = "rlang_zap")
#>   compile_steps_per_execution = structure(list(), class = "rlang_zap")
#>   compile_jit_compile = structure(list(), class = "rlang_zap")
#>   compile_auto_scale_loss = structure(list(), class = "rlang_zap")
#> 
#> Computational engine: keras

Define Tuning Grid

We will create a regular grid for our hyperparameters.

# Define the tuning grid
params <- extract_parameter_set_dials(penguin_wf) |>
  update(
    hidden_1_units = hidden_units(range = c(32, 128)),
    hidden_1_rate = dropout(range = c(0.1, 0.4)),
    hidden_2_units = hidden_units(range = c(16, 64)),
    hidden_2_rate = dropout(range = c(0.1, 0.4))
  )
mlp_grid <- grid_regular(params, levels = 3)

print(mlp_grid)
#> # A tibble: 81 × 4
#>    hidden_1_units hidden_1_rate hidden_2_units hidden_2_rate
#>             <int>         <dbl>          <int>         <dbl>
#>  1             32         0.1               16           0.1
#>  2             80         0.1               16           0.1
#>  3            128         0.1               16           0.1
#>  4             32         0.25              16           0.1
#>  5             80         0.25              16           0.1
#>  6            128         0.25              16           0.1
#>  7             32         0.400             16           0.1
#>  8             80         0.400             16           0.1
#>  9            128         0.400             16           0.1
#> 10             32         0.1               40           0.1
#> # ℹ 71 more rows

Tune Model

Now, we’ll use tune_race_anova() to perform cross-validation and find the best hyperparameters.

# Note: Parallel processing with `plan(multisession)` is currently not working
# with Keras models due to backend conflicts

set.seed(123)
penguin_tune_results <- tune_race_anova(
  penguin_wf,
  resamples = penguin_folds,
  grid = mlp_grid,
  metrics = metric_set(accuracy, roc_auc, f_meas),
  control = control_race(save_pred = TRUE, save_workflow = TRUE)
)
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 31ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 31ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 33ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 31ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 35ms/step
#> 2/2 - 0s - 14ms/step
#> 2/2 - 0s - 32ms/step
#> 2/2 - 0s - 13ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 33ms/step
#> 2/2 - 0s - 14ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 12ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 10ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 29ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 30ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 28ms/step
#> 2/2 - 0s - 11ms/step
#> 2/2 - 0s - 27ms/step
#> 2/2 - 0s - 10ms/step

Inspect Tuning Results

We can inspect the tuning results to see which hyperparameter combinations performed best.

# Show the best performing models based on accuracy
show_best(penguin_tune_results, metric = "accuracy", n = 5)
#> # A tibble: 5 × 10
#>   hidden_1_units hidden_1_rate hidden_2_units hidden_2_rate .metric  .estimator
#>            <int>         <dbl>          <int>         <dbl> <chr>    <chr>     
#> 1             32         0.1               16           0.1 accuracy multiclass
#> 2             80         0.1               16           0.1 accuracy multiclass
#> 3            128         0.25              16           0.1 accuracy multiclass
#> 4            128         0.400             16           0.1 accuracy multiclass
#> 5             32         0.1               40           0.1 accuracy multiclass
#> # ℹ 4 more variables: mean <dbl>, n <int>, std_err <dbl>, .config <chr>

# Autoplot the results
# Currently does not work due to a label issue: autoplot(penguin_tune_results)

# Select the best hyperparameters
best_mlp_params <- select_best(penguin_tune_results, metric = "accuracy")
print(best_mlp_params)
#> # A tibble: 1 × 5
#>   hidden_1_units hidden_1_rate hidden_2_units hidden_2_rate .config             
#>            <int>         <dbl>          <int>         <dbl> <chr>               
#> 1             32           0.1             16           0.1 Preprocessor1_Model…

Finalize Workflow and Fit Model

Once we have the best hyperparameters, we finalize the workflow and fit the model on the entire training dataset.

# Finalize the workflow with the best hyperparameters
final_penguin_wf <- finalize_workflow(penguin_wf, best_mlp_params)

# Fit the final model on the full training data
final_penguin_fit <- fit(final_penguin_wf, data = penguin_train)

print(final_penguin_fit)
#> ══ Workflow [trained] ══════════════════════════════════════════════════════════
#> Preprocessor: Recipe
#> Model: penguin_mlp()
#> 
#> ── Preprocessor ────────────────────────────────────────────────────────────────
#> 2 Recipe Steps
#> 
#> • step_normalize()
#> • step_dummy()
#> 
#> ── Model ───────────────────────────────────────────────────────────────────────
#> $fit
#> Model: "sequential_405"
#> ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
#> ┃ Layer (type)                      ┃ Output Shape             ┃       Param # ┃
#> ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
#> │ dense_1215 (Dense)                │ (None, 32)               │           256 │
#> ├───────────────────────────────────┼──────────────────────────┼───────────────┤
#> │ dropout_810 (Dropout)             │ (None, 32)               │             0 │
#> ├───────────────────────────────────┼──────────────────────────┼───────────────┤
#> │ dense_1216 (Dense)                │ (None, 16)               │           528 │
#> ├───────────────────────────────────┼──────────────────────────┼───────────────┤
#> │ dropout_811 (Dropout)             │ (None, 16)               │             0 │
#> ├───────────────────────────────────┼──────────────────────────┼───────────────┤
#> │ dense_1217 (Dense)                │ (None, 3)                │            51 │
#> └───────────────────────────────────┴──────────────────────────┴───────────────┘
#>  Total params: 2,507 (9.80 KB)
#>  Trainable params: 835 (3.26 KB)
#>  Non-trainable params: 0 (0.00 B)
#>  Optimizer params: 1,672 (6.54 KB)
#> 
#> $history
#> 
#> Final epoch (plot to see history):
#>     accuracy: 1
#>         loss: 0.006855
#> val_accuracy: 1
#>     val_loss: 0.00003971 
#> 
#> $lvl
#> [1] "Adelie"    "Chinstrap" "Gentoo"   
#> 
#> $process_x
#> function (x) 
#> {
#>     if (is.data.frame(x) && ncol(x) == 1 && is.list(x[[1]])) {
#>         x_proc <- do.call(abind::abind, c(x[[1]], list(along = 0)))
#>     }
#>     else {
#>         x_proc <- as.matrix(x)
#>     }
#>     input_shape <- if (length(dim(x_proc)) > 2) 
#>         dim(x_proc)[-1]
#>     else ncol(x_proc)
#>     list(x_proc = x_proc, input_shape = input_shape)
#> }
#> <bytecode: 0x561ad60c81a0>
#> <environment: namespace:kerasnip>
#> 
#> $process_y
#> function (y, is_classification = NULL, class_levels = NULL) 
#> 
#> ...
#> and 27 more lines.

Inspect Final Model

You can extract the underlying Keras model and its training history for further inspection.

# Extract the Keras model summary
final_penguin_fit |>
  extract_fit_parsnip() |>
  extract_keras_model() |>
  summary()
#> Model: "sequential_405"
#> ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
#> ┃ Layer (type)                      ┃ Output Shape             ┃       Param # ┃
#> ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
#> │ dense_1215 (Dense)                │ (None, 32)               │           256 │
#> ├───────────────────────────────────┼──────────────────────────┼───────────────┤
#> │ dropout_810 (Dropout)             │ (None, 32)               │             0 │
#> ├───────────────────────────────────┼──────────────────────────┼───────────────┤
#> │ dense_1216 (Dense)                │ (None, 16)               │           528 │
#> ├───────────────────────────────────┼──────────────────────────┼───────────────┤
#> │ dropout_811 (Dropout)             │ (None, 16)               │             0 │
#> ├───────────────────────────────────┼──────────────────────────┼───────────────┤
#> │ dense_1217 (Dense)                │ (None, 3)                │            51 │
#> └───────────────────────────────────┴──────────────────────────┴───────────────┘
#>  Total params: 2,507 (9.80 KB)
#>  Trainable params: 835 (3.26 KB)
#>  Non-trainable params: 0 (0.00 B)
#>  Optimizer params: 1,672 (6.54 KB)

# Plot the Keras model
final_penguin_fit |>
  extract_fit_parsnip() |>
  extract_keras_model() |>
  plot(show_shapes = TRUE)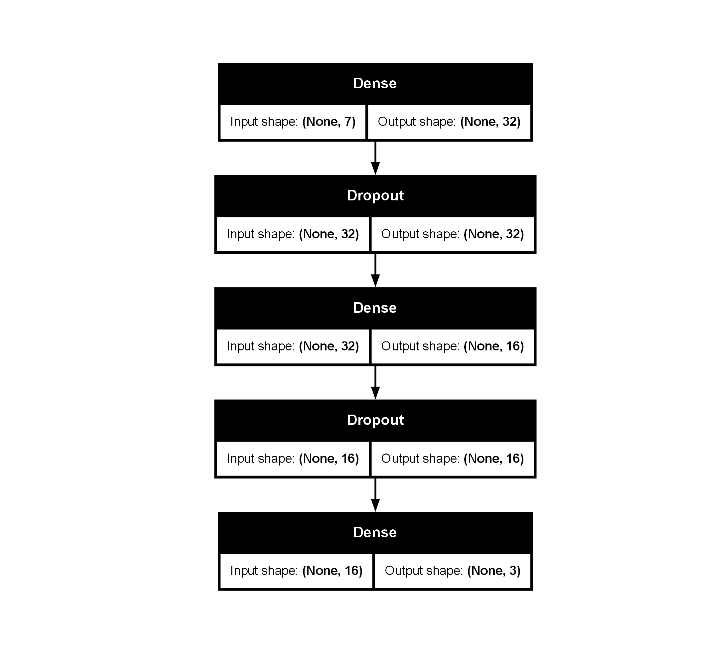

Model

# Plot the training history
final_penguin_fit |>
  extract_fit_parsnip() |>
  extract_keras_history() |>
  plot()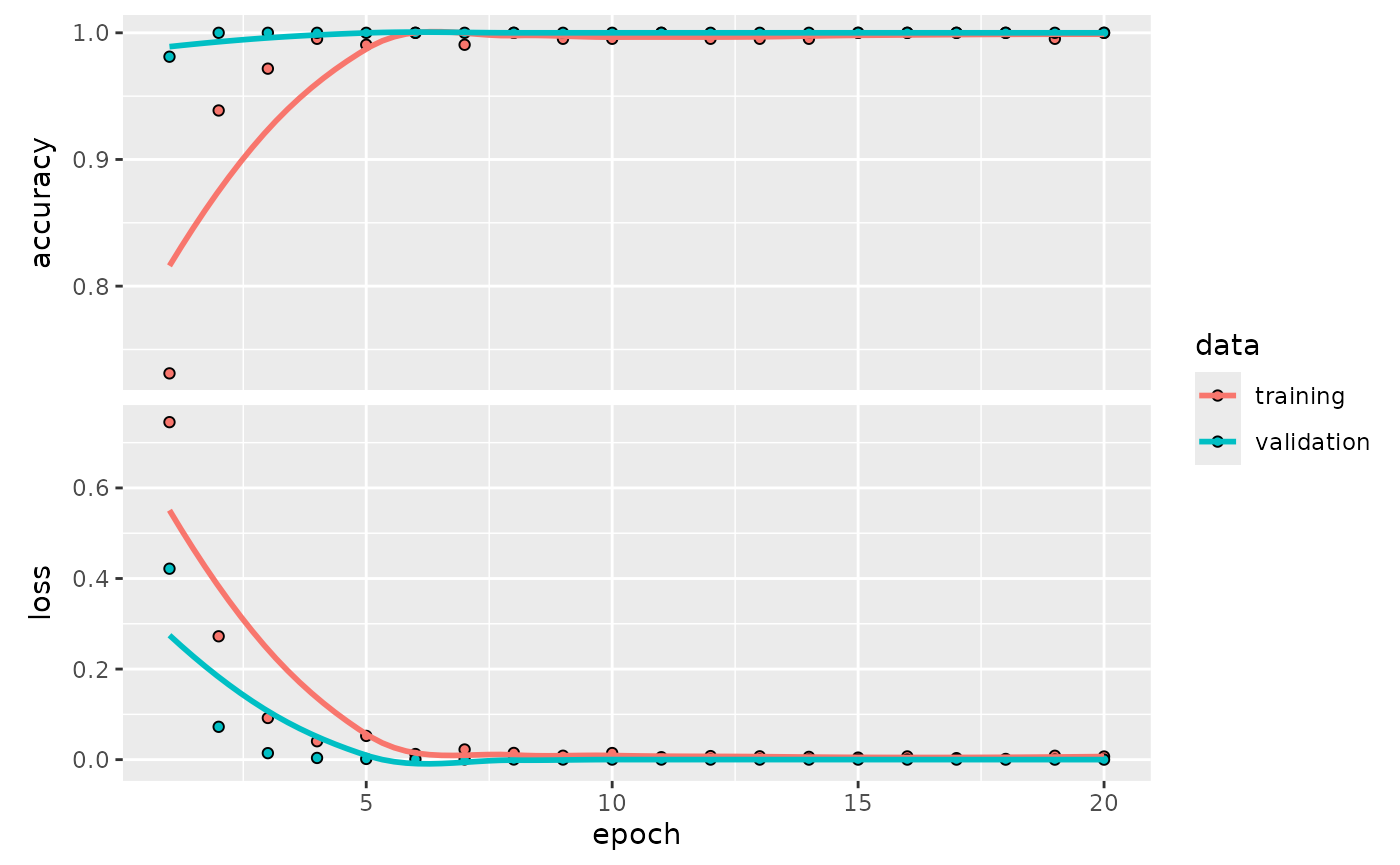

Make Predictions and Evaluate

Finally, we will make predictions on the test set and evaluate the model’s performance.

# Make predictions on the test set
penguin_test_pred <- predict(final_penguin_fit, new_data = penguin_test)
#> 3/3 - 0s - 19ms/step
penguin_test_prob <- predict(
  final_penguin_fit,
  new_data = penguin_test,
  type = "prob"
)
#> 3/3 - 0s - 7ms/step

# Combine predictions with actuals
penguin_results <- penguin_test |>
  select(species) |>
  bind_cols(penguin_test_pred, penguin_test_prob)

print(head(penguin_results))
#> # A tibble: 6 × 5
#>   species .pred_class .pred_Adelie .pred_Chinstrap .pred_Gentoo
#>   <fct>   <fct>              <dbl>           <dbl>        <dbl>
#> 1 Adelie  Adelie             1.000        3.19e-10     2.90e- 9
#> 2 Adelie  Adelie             1.000        1.19e- 6     3.08e- 6
#> 3 Adelie  Adelie             1.000        1.92e-11     1.91e-10
#> 4 Adelie  Adelie             1.000        3.56e- 9     3.05e- 8
#> 5 Adelie  Adelie             1.000        4.87e- 9     5.28e- 8
#> 6 Adelie  Adelie             1.000        6.26e- 9     1.48e- 7

# Evaluate performance using yardstick metrics
metrics_results <- metric_set(
  accuracy,
  roc_auc,
  f_meas
)(
  penguin_results,
  truth = species,
  estimate = .pred_class,
  .pred_Adelie,
  .pred_Chinstrap,
  .pred_Gentoo
)

print(metrics_results)
#> # A tibble: 3 × 3
#>   .metric  .estimator .estimate
#>   <chr>    <chr>          <dbl>
#> 1 accuracy multiclass     0.985
#> 2 f_meas   macro          0.983
#> 3 roc_auc  hand_till      0.999

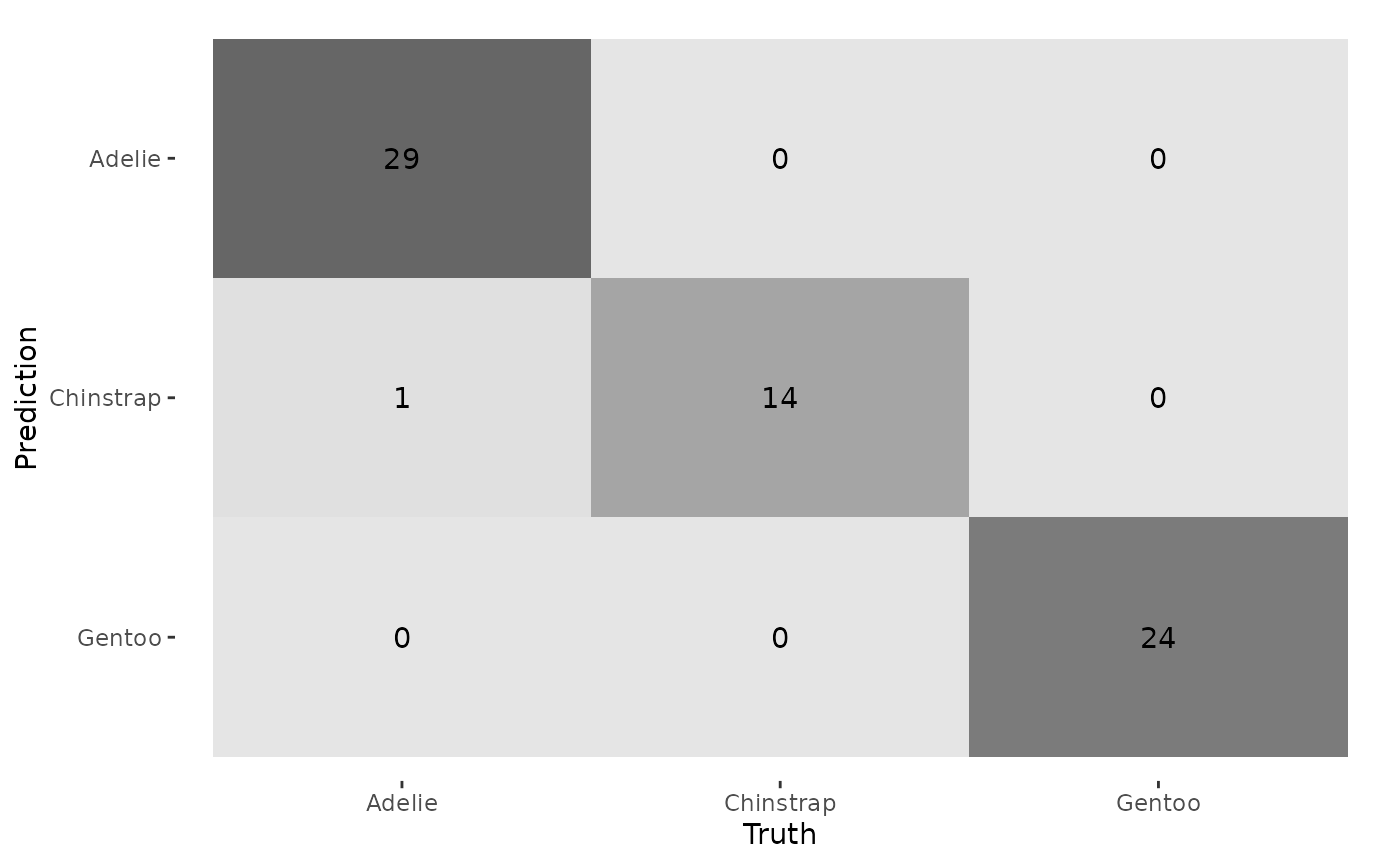
# Confusion Matrix
conf_mat(penguin_results, truth = species, estimate = .pred_class) |>
  autoplot(type = "heatmap")