18 Expresiones

18.1 Introducción

Para calcular el lenguaje, primero necesitamos entender su estructura. Eso requiere un vocabulario nuevo, algunas herramientas nuevas y algunas formas nuevas de pensar sobre el código R. El primero de ellos es la distinción entre una operación y su resultado. Toma el siguiente código, que multiplica una variable x por 10 y guarda el resultado en una nueva variable llamada y. No funciona porque no hemos definido una variable llamada x:

y <- x * 10
#> Error in eval(expr, envir, enclos): object 'x' not found

Sería bueno si pudiéramos capturar la intención del código sin ejecutarlo. En otras palabras, ¿cómo podemos separar nuestra descripción de la acción de la acción misma?

Una forma es usar rlang::expr():

z <- rlang::expr(y <- x * 10)
z
#> y <- x * 10

expr() devuelve una expresión, un objeto que captura la estructura del código sin evaluarlo (es decir, ejecutarlo). Si tiene una expresión, puede evaluarla con base::eval():

x <- 4
eval(z)
y
#> [1] 40

El enfoque de este capítulo son las estructuras de datos que subyacen a las expresiones. Dominar este conocimiento le permitirá inspeccionar y modificar el código capturado y generar código con código. Volveremos a expr() en el Capítulo 19, ya eval() en el Capítulo 20.

Estructura

La Sección 18.2 introduce la idea del árbol de sintaxis abstracta (AST) y revela la estructura de árbol que subyace en todo el código R.
La Sección 18.3 se sumerge en los detalles de las estructuras de datos que sustentan el AST: constantes, símbolos y llamadas, que se conocen colectivamente como expresiones.
La Sección 18.4 cubre el análisis, el acto de convertir la secuencia lineal de caracteres en código en AST, y usa esa idea para explorar algunos detalles de la gramática de R.
La Sección 18.5 le muestra cómo puede usar funciones recursivas para calcular en el lenguaje, escribiendo funciones que calculan con expresiones.
La Sección 18.6 vuelve a tres estructuras de datos más especializadas: listas de pares, argumentos perdidos y vectores de expresión.

Requisitos previos

Asegúrese de haber leído la descripción general de la metaprogramación en el Capítulo 17 para obtener una descripción general amplia de la motivación y el vocabulario básico. También necesitará el paquete rlang para capturar y calcular expresiones, y el paquete lobstr para visualizarlos.

library(rlang)
library(lobstr)

18.2 Árboles de sintaxis abstracta

Las expresiones también se denominan árboles de sintaxis abstracta (AST) porque la estructura del código es jerárquica y se puede representar naturalmente como un árbol. Comprender esta estructura de árbol es crucial para inspeccionar y modificar expresiones (es decir, metaprogramación).

18.2.1 Dibujo

Comenzaremos presentando algunas convenciones para dibujar AST, comenzando con una simple llamada que muestra sus componentes principales: f(x, "y", 1). Dibujaré árboles de dos maneras¹:

A “mano” (es decir, con OmniGraffle):

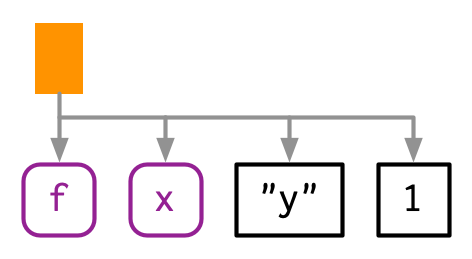
Con lobstr::ast():

lobstr::ast(f(x, "y", 1))
#> █─f 
#> ├─x 
#> ├─"y" 
#> └─1

Ambos enfoques comparten convenciones tanto como sea posible:

Las hojas del árbol son símbolos, como f y x, o constantes, como 1 o "y". Los símbolos se dibujan en púrpura y tienen esquinas redondeadas. Las constantes tienen bordes negros y esquinas cuadradas. Las cadenas y los símbolos se confunden fácilmente, por lo que las cadenas siempre se escriben entre comillas.
Las ramas del árbol son objetos de llamada, que representan llamadas de función y se dibujan como rectángulos naranjas. El primer hijo (f) es la función que se llama; el segundo hijo y los subsiguientes (x, "y" y 1) son los argumentos de esa función.

Los colores se mostrarán cuando usted llame a ast(), pero no aparecen en el libro por razones técnicas complicadas.

El ejemplo anterior solo contenía una llamada de función, lo que lo convierte en un árbol muy poco profundo. La mayoría de las expresiones contendrán considerablemente más llamadas, creando árboles con múltiples niveles. Por ejemplo, considere el AST para f(g(1, 2), h(3, 4, i())):

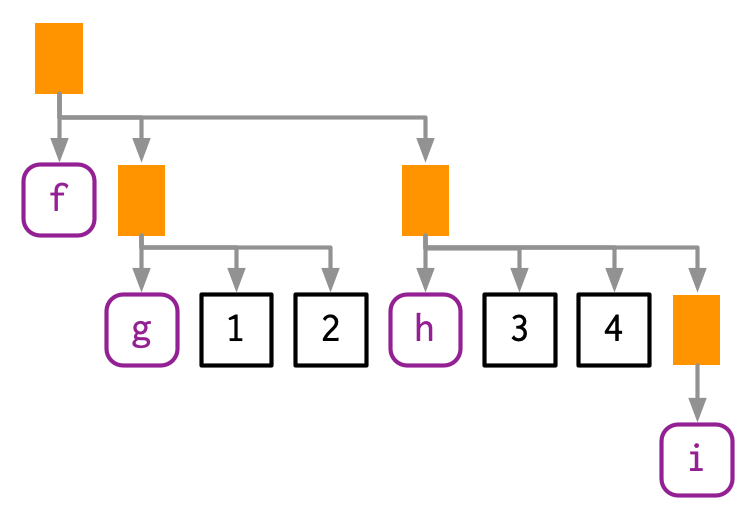
lobstr::ast(f(g(1, 2), h(3, 4, i())))
#> █─f 
#> ├─█─g 
#> │ ├─1 
#> │ └─2 
#> └─█─h 
#>   ├─3 
#>   ├─4 
#>   └─█─i

Puede leer los diagramas dibujados a mano de izquierda a derecha (ignorando la posición vertical) y los diagramas dibujados por langosta de arriba a abajo (ignorando la posición horizontal). La profundidad dentro del árbol está determinada por el anidamiento de las llamadas a funciones. Esto también determina el orden de evaluación, ya que la evaluación generalmente procede de lo más profundo a lo más superficial, pero esto no está garantizado debido a la evaluación diferida (Sección 6.5). También tenga en cuenta la aparición de i(), una llamada de función sin argumentos; es una rama con una sola hoja (símbolo).

18.2.2 Componentes sin código

Es posible que se haya preguntado qué hace que estos árboles de sintaxis abstractos. Son abstractos porque solo capturan detalles estructurales importantes del código, no espacios en blanco ni comentarios:

ast(
  f(x,  y)  # important!
)
#> █─f 
#> ├─x 
#> └─y

Solo hay un lugar donde los espacios en blanco afectan el AST:

lobstr::ast(y <- x)
#> █─`<-` 
#> ├─y 
#> └─x
lobstr::ast(y < -x)
#> █─`<` 
#> ├─y 
#> └─█─`-` 
#>   └─x

18.2.3 Llamadas infijas

Cada llamada en R se puede escribir en forma de árbol porque cualquier llamada se puede escribir en forma de prefijo (Sección 6.8.1). Tome y <- x * 10 de nuevo: ¿cuáles son las funciones que se están llamando? No es tan fácil de detectar como f(x, 1) porque esta expresión contiene dos llamadas infijas: <- y *. Eso significa que estas dos líneas de código son equivalentes:

y <- x * 10
`<-`(y, `*`(x, 10))

Y ambas tienen este AST²:

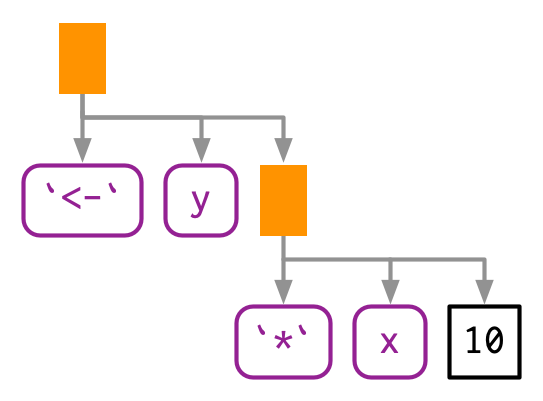
lobstr::ast(y <- x * 10)
#> █─`<-` 
#> ├─y 
#> └─█─`*` 
#>   ├─x 
#>   └─10

Realmente no hay diferencia entre los AST, y si genera una expresión con llamadas de prefijo, R aún la imprimirá en forma de infijo:

expr(`<-`(y, `*`(x, 10)))
#> y <- x * 10

El orden en que se aplican los operadores infijos se rige por un conjunto de reglas llamadas precedencia de operadores, y usaremos lobstr::ast() para explorarlas en la Sección 18.4.1.

18.2.4 Ejercicios

Reconstruya el código representado por los árboles a continuación:

#> █─f 
#> └─█─g 
#>   └─█─h
#> █─`+` 
#> ├─█─`+` 
#> │ ├─1 
#> │ └─2 
#> └─3
#> █─`*` 
#> ├─█─`(` 
#> │ └─█─`+` 
#> │   ├─x 
#> │   └─y 
#> └─z

Dibuja los siguientes árboles a mano y luego verifica tus respuestas con lobstr::ast().
```
f(g(h(i(1, 2, 3))))
f(1, g(2, h(3, i())))
f(g(1, 2), h(3, i(4, 5)))
```

¿Qué está pasando con los AST a continuación? (Sugerencia: lea atentamente ?"^".)

lobstr::ast(`x` + `y`)
#> █─`+` 
#> ├─x 
#> └─y
lobstr::ast(x ** y)
#> █─`^` 
#> ├─x 
#> └─y
lobstr::ast(1 -> x)
#> █─`<-` 
#> ├─x 
#> └─1

¿Qué está pasando con los AST a continuación? (Sugerencia: lea atentamente la Sección 6.2.1.)

lobstr::ast(function(x = 1, y = 2) {})
#> █─`function` 
#> ├─█─x = 1 
#> │ └─y = 2 
#> ├─█─`{` 
#> └─<inline srcref>

¿Cómo se ve el árbol de llamadas de una instrucción if con múltiples condiciones else if? ¿Por qué?

18.3 Expresiones

En conjunto, las estructuras de datos presentes en el AST se denominan expresiones. Una expresión es cualquier miembro del conjunto de tipos base creados mediante el código de análisis: escalares constantes, símbolos, objetos de llamada y listas de pares. Estas son las estructuras de datos utilizadas para representar el código capturado de expr(), y is_expression(expr(...)) siempre es verdadero. Las constantes, los símbolos y los objetos de llamada son los más importantes y se analizan a continuación. Las listas de pares y los símbolos vacíos son más especializados y volveremos a ellos en las secciones Sección 18.6.1 y Sección 18.6.2.

NB: En la documentación base de R, “expresión” se usa para significar dos cosas. Además de la definición anterior, expresión también se usa para referirse al tipo de objeto devuelto por expression() y parse(), que son básicamente listas de expresiones como se define anteriormente. En este libro llamaré a estos vectores de expresión, y regresaré a ellos en la Sección 18.6.3.

18.3.1 Constantes

Las constantes escalares son el componente más simple del AST. Más precisamente, una constante es NULL o un vector atómico de longitud 1 (o escalar, Sección 3.2.1) como TRUE, 1L, 2.5 o "x". Puedes probar una constante con rlang::is_syntactic_literal().

Las constantes son autocomillas en el sentido de que la expresión utilizada para representar una constante es la misma constante:

identical(expr(TRUE), TRUE)
#> [1] TRUE
identical(expr(1), 1)
#> [1] TRUE
identical(expr(2L), 2L)
#> [1] TRUE
identical(expr("x"), "x")
#> [1] TRUE

18.3.2 Simbolos

Un símbolo representa el nombre de un objeto como x, mtcars o mean. En la base R, los términos símbolo y nombre se usan indistintamente (es decir, is.name() es idéntico a is.symbol()), pero en este libro usé símbolo de manera consistente porque “nombre” tiene muchos otros significados.

Puede crear un símbolo de dos maneras: capturando el código que hace referencia a un objeto con expr(), o convirtiendo una cadena en un símbolo con rlang::sym():

expr(x)
#> x
sym("x")
#> x

Puede volver a convertir un símbolo en una cadena con as.character() o rlang::as_string(). as_string() tiene la ventaja de indicar claramente que obtendrá un vector de caracteres de longitud 1.

as_string(expr(x))
#> [1] "x"

Puede reconocer un símbolo porque está impreso sin comillas, str() le dice que es un símbolo, y is.symbol() es TRUE:

str(expr(x))
#>  symbol x
is.symbol(expr(x))
#> [1] TRUE

El tipo de símbolo no está vectorizado, es decir, un símbolo siempre tiene una longitud de 1. Si desea varios símbolos, deberá ponerlos en una lista usando (p. ej.) rlang::syms().

18.3.3 Llamadas

Un objeto de llamada representa una llamada de función capturada. Los objetos de llamada son un tipo especial de lista donde el primer componente especifica la función a llamar (generalmente un símbolo), y los elementos restantes son los argumentos para esa llamada. Los objetos de llamada crean ramas en el AST, porque las llamadas se pueden anidar dentro de otras llamadas.

Puede identificar un objeto de llamada cuando se imprime porque parece una llamada de función. Confusamente typeof() y str() imprimen “lenguaje” para los objetos de llamada, pero is.call() devuelve TRUE:

lobstr::ast(read.table("important.csv", row.names = FALSE))
#> █─read.table 
#> ├─"important.csv" 
#> └─row.names = FALSE
x <- expr(read.table("important.csv", row.names = FALSE))

typeof(x)
#> [1] "language"
is.call(x)
#> [1] TRUE

18.3.3.1 Subconjunto

Las llamadas generalmente se comportan como listas, es decir, puede usar herramientas estándar de creación de subconjuntos. El primer elemento del objeto de llamada es la función a llamar, que suele ser un símbolo:

x[[1]]
#> read.table
is.symbol(x[[1]])
#> [1] TRUE

El resto de los elementos son los argumentos:

as.list(x[-1])
#> [[1]]
#> [1] "important.csv"
#> 
#> $row.names
#> [1] FALSE

Puede extraer argumentos individuales con [[ o, si se nombra, $:

x[[2]]
#> [1] "important.csv"
x$row.names
#> [1] FALSE

Puede determinar la cantidad de argumentos en un objeto de llamada restando 1 de su longitud:

length(x) - 1
#> [1] 2

Extraer argumentos específicos de las llamadas es un desafío debido a las reglas flexibles de R para la coincidencia de argumentos: potencialmente podría estar en cualquier ubicación, con el nombre completo, con un nombre abreviado o sin nombre. Para solucionar este problema, puede usar rlang::call_standardise() que estandariza todos los argumentos para usar el nombre completo:

rlang::call_standardise(x)
#> Warning: `call_standardise()` is deprecated as of rlang 0.4.11
#> This warning is displayed once every 8 hours.
#> read.table(file = "important.csv", row.names = FALSE)

(NB: Si la función usa ... no es posible estandarizar todos los argumentos).

Las llamadas se pueden modificar de la misma forma que las listas:

x$header <- TRUE
x
#> read.table("important.csv", row.names = FALSE, header = TRUE)

18.3.3.2 Posición de la función

El primer elemento del objeto de llamada es la posición de la función. Contiene la función que se llamará cuando se evalúe el objeto, y generalmente es un símbolo ³:

lobstr::ast(foo())
#> █─foo

Mientras que R le permite rodear el nombre de la función con comillas, el analizador lo convierte en un símbolo:

lobstr::ast("foo"())
#> █─foo

Sin embargo, a veces la función no existe en el entorno actual y es necesario realizar algunos cálculos para recuperarla: por ejemplo, si la función está en otro paquete, es un método de un objeto R6 o es creada por una fábrica de funciones. En este caso, la posición de la función será ocupada por otra llamada:

lobstr::ast(pkg::foo(1))
#> █─█─`::` 
#> │ ├─pkg 
#> │ └─foo 
#> └─1
lobstr::ast(obj$foo(1))
#> █─█─`$` 
#> │ ├─obj 
#> │ └─foo 
#> └─1
lobstr::ast(foo(1)(2))
#> █─█─foo 
#> │ └─1 
#> └─2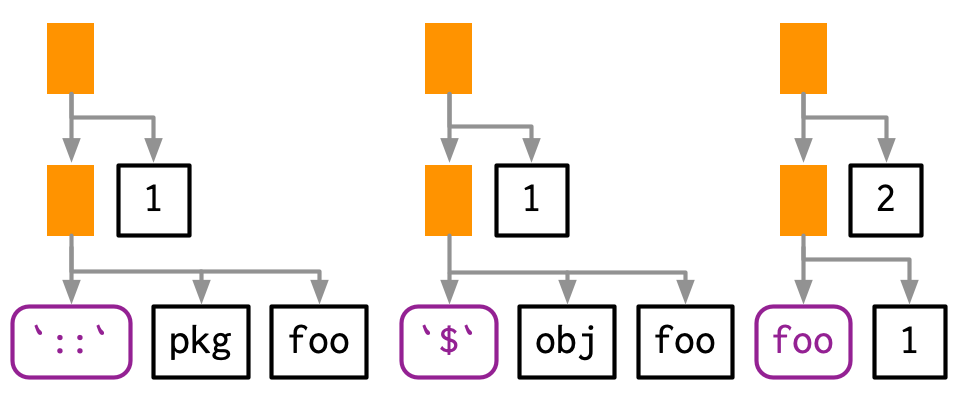

18.3.3.3 Construyendo

Puede construir un objeto de llamada a partir de sus componentes utilizando rlang::call2(). El primer argumento es el nombre de la función a llamar (ya sea como una cadena, un símbolo u otra llamada). Los argumentos restantes se pasarán a la llamada:

call2("mean", x = expr(x), na.rm = TRUE)
#> mean(x = x, na.rm = TRUE)
call2(expr(base::mean), x = expr(x), na.rm = TRUE)
#> base::mean(x = x, na.rm = TRUE)

Las llamadas de infijo creadas de esta manera aún se imprimen como de costumbre.

call2("<-", expr(x), 10)
#> x <- 10

Usar call2() para crear expresiones complejas es un poco torpe. Aprenderás otra técnica en el Capítulo 19.

18.3.4 Resumen

La siguiente tabla resume la apariencia de los diferentes subtipos de expresión en str() y typeof():

	`str()`	`typeof()`
constante escalar	`logi`/`int`/`num`/`chr`	`logical`/`integer`/`double`/`character`
Símbolo	`symbol`	`symbol`
Objeto de llamada	`language`	`language`
Lista de pares	Lista de pares punteados	`pairlist`
Vector de expresión	`expression()`	`expression`

Tanto base R como rlang proporcionan funciones para probar cada tipo de entrada, aunque los tipos cubiertos son ligeramente diferentes. Puede distinguirlas fácilmente porque todas las funciones básicas comienzan con is. y las funciones rlang comienzan con is_.

	base	rlang
Scalar constant	—	`is_syntactic_literal()`
Symbol	`is.symbol()`	`is_symbol()`
Call object	`is.call()`	`is_call()`
Pairlist	`is.pairlist()`	`is_pairlist()`
Expression vector	`is.expression()`	—

18.3.5 Ejercicios

¿Cuáles dos de los seis tipos de vectores atómicos no pueden aparecer en una expresión? ¿Por qué? De manera similar, ¿por qué no puedes crear una expresión que contenga un vector atómico de longitud mayor que uno?
¿Qué sucede cuando crea un subconjunto de un objeto de llamada para eliminar el primer elemento? p.ej. expr(read.csv("foo.csv", header = TRUE))[-1]. ¿Por qué?

Describa las diferencias entre los siguientes objetos de llamada.

x <- 1:10

call2(median, x, na.rm = TRUE)
call2(expr(median), x, na.rm = TRUE)
call2(median, expr(x), na.rm = TRUE)
call2(expr(median), expr(x), na.rm = TRUE)

rlang::call_standardise() no funciona tan bien para las siguientes llamadas. ¿Por qué? ¿Qué hace especial a mean()?

call_standardise(quote(mean(1:10, na.rm = TRUE)))
#> mean(x = 1:10, na.rm = TRUE)
call_standardise(quote(mean(n = T, 1:10)))
#> mean(x = 1:10, n = T)
call_standardise(quote(mean(x = 1:10, , TRUE)))
#> mean(x = 1:10, , TRUE)

¿Por qué este código no tiene sentido?

x <- expr(foo(x = 1))
names(x) <- c("x", "y")

Construya la expresión if(x > 1) "a" else "b" utilizando varias llamadas a call2(). ¿Cómo refleja la estructura del código la estructura del AST?

18.4 Análisis y gramática

Hemos hablado mucho sobre las expresiones y el AST, pero no sobre cómo se crean las expresiones a partir del código que escribe (como "x + y"). El proceso mediante el cual un lenguaje informático toma una cadena y construye una expresión se denomina análisis sintáctico y se rige por un conjunto de reglas conocido como gramática. En esta sección, usaremos lobstr::ast() para explorar algunos de los detalles de la gramática de R, y luego mostraremos cómo puede transformar de un lado a otro entre expresiones y cadenas.

18.4.1 Predecencia de operadores

Las funciones infijas introducen dos fuentes de ambigüedad. La primera fuente de ambigüedad surge de las funciones infijas: ¿qué produce 1 + 2 * 3? ¿Obtienes 9 (es decir, (1 + 2) * 3), o 7 (es decir, 1 + (2 * 3))? En otras palabras, ¿cuál de los dos posibles árboles de análisis de abajo usa R?

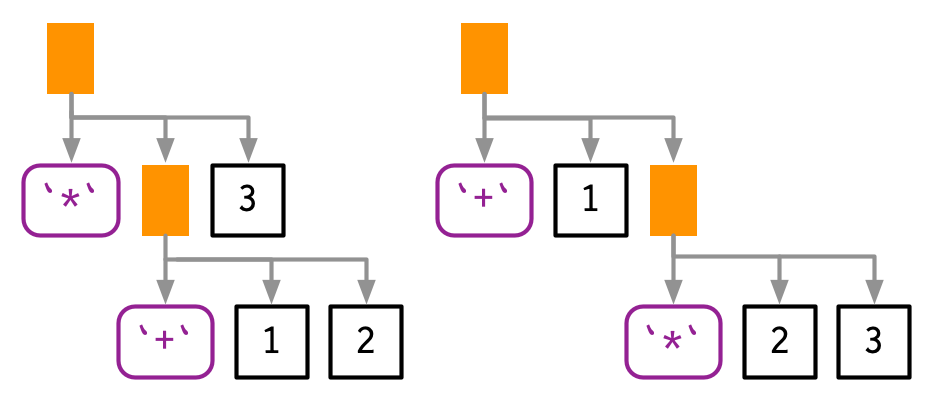
Los lenguajes de programación usan convenciones llamadas precedencia de operadores para resolver esta ambigüedad. Podemos usar ast() para ver qué hace R:

lobstr::ast(1 + 2 * 3)
#> █─`+` 
#> ├─1 
#> └─█─`*` 
#>   ├─2 
#>   └─3

Predicting the precedence of arithmetic operations is usually easy because it’s drilled into you in school and is consistent across the vast majority of programming languages.

Predecir la precedencia de otros operadores es más difícil. Hay un caso particularmente sorprendente en R: ! tiene una precedencia mucho menor (es decir, se une con menos fuerza) de lo que cabría esperar. Esto le permite escribir operaciones útiles como:

lobstr::ast(!x %in% y)
#> █─`!` 
#> └─█─`%in%` 
#>   ├─x 
#>   └─y

R tiene más de 30 operadores infijos divididos en 18 grupos de precedencia. Si bien los detalles se describen en ?Syntax, muy pocas personas han memorizado el orden completo. Si hay alguna confusión, ¡use paréntesis!

lobstr::ast((1 + 2) * 3)
#> █─`*` 
#> ├─█─`(` 
#> │ └─█─`+` 
#> │   ├─1 
#> │   └─2 
#> └─3

Tenga en cuenta la aparición de los paréntesis en el AST como una llamada a la función (.

18.4.2 Asociatividad

La segunda fuente de ambigüedad se presenta por el uso repetido de la misma función de infijo. Por ejemplo, ¿es ‘1 + 2 + 3’ equivalente a ‘(1 + 2) + 3’ o a ‘1 + (2 + 3)’? Esto normalmente no importa porque x + (y + z) == (x + y) + z, es decir, la suma es asociativa, pero es necesaria porque algunas clases de S3 definen + de forma no asociativa. Por ejemplo, ggplot2 sobrecarga + para construir una trama compleja a partir de piezas simples; esto no es asociativo porque las capas anteriores se dibujan debajo de las capas posteriores (es decir, geom_point() + geom_smooth() no produce el mismo gráfico que geom_smooth() + geom_point()).

En R, la mayoría de los operadores son asociativos a la izquierda, es decir, las operaciones de la izquierda se evalúan primero:

lobstr::ast(1 + 2 + 3)
#> █─`+` 
#> ├─█─`+` 
#> │ ├─1 
#> │ └─2 
#> └─3

Hay dos excepciones: exponenciación y asignación.

lobstr::ast(2^2^3)
#> █─`^` 
#> ├─2 
#> └─█─`^` 
#>   ├─2 
#>   └─3
lobstr::ast(x <- y <- z)
#> █─`<-` 
#> ├─x 
#> └─█─`<-` 
#>   ├─y 
#>   └─z

18.4.3 Analizar y desanalizar

La mayoría de las veces, escribe código en la consola y R se encarga de convertir los caracteres que ha escrito en un AST. Pero ocasionalmente tiene código almacenado en una cadena y desea analizarlo usted mismo. Puedes hacerlo usando rlang::parse_expr():

x1 <- "y <- x + 10"
x1
#> [1] "y <- x + 10"
is.call(x1)
#> [1] FALSE

x2 <- rlang::parse_expr(x1)
x2
#> y <- x + 10
is.call(x2)
#> [1] TRUE

parse_expr() siempre devuelve una sola expresión. Si tiene varias expresiones separadas por ; o \n, deberá usar rlang::parse_exprs(). Devuelve una lista de expresiones:

x3 <- "a <- 1; a + 1"
rlang::parse_exprs(x3)
#> [[1]]
#> a <- 1
#> 
#> [[2]]
#> a + 1

Si se encuentra trabajando con cadenas que contienen código con mucha frecuencia, debe reconsiderar su proceso. Lea el Capítulo 19 y considere si puede generar expresiones utilizando la cuasicita de manera más segura.

El equivalente básico de parse_exprs() es parse(). Es un poco más difícil de usar porque está especializado para analizar código R almacenado en archivos. Debe proporcionar su cadena al argumento texto y devolverá un vector de expresión (Sección 18.6.3). Recomiendo convertir la salida en una lista:

as.list(parse(text = x1))
#> [[1]]
#> y <- x + 10

Lo contrario de analizar es deparsear: dada una expresión, desea la cadena que la generaría. Esto sucede automáticamente cuando imprime una expresión, y puede obtener la cadena con rlang::expr_text():

z <- expr(y <- x + 10)
expr_text(z)
#> [1] "y <- x + 10"

El análisis y la eliminación no son perfectamente simétricos porque el análisis genera un árbol de sintaxis abstracto. Esto significa que perdemos los acentos graves en los nombres, comentarios y espacios en blanco ordinarios:

cat(expr_text(expr({
  # This is a comment
  x <-             `x` + 1
})))
#> {
#>     x <- x + 1
#> }

Tenga cuidado al usar el equivalente base R, deparse(): devuelve un vector de caracteres con un elemento para cada línea. Siempre que lo use, recuerde que la longitud de la salida puede ser mayor que uno y planifique en consecuencia.

18.4.4 Ejercicios

R usa paréntesis de dos maneras ligeramente diferentes, como se ilustra en estas dos llamadas:
```
f((1))
`(`(1 + 1)
```
Compare y contraste los dos usos haciendo referencia al AST.
= también se puede utilizar de dos maneras. Construya un ejemplo simple que muestre ambos usos.
¿-2^2 produce 4 o -4? ¿Por qué?
¿Qué devuelve !1 + !1? ¿Por qué?
¿Por qué x1 <- x2 <- x3 <- 0 funciona? Describe las dos razones.
Compara los AST de x + y %+% z y x ^ y %+% z. ¿Qué has aprendido sobre la precedencia de las funciones de infijo personalizadas?
¿Qué sucede si llamas a parse_expr() con una cadena que genera múltiples expresiones? p.ej. parse_expr("x + 1; y + 1")
¿Qué sucede si intenta analizar una expresión no válida? p.ej. "a +" o "f())".

deparse() produce vectores cuando la entrada es larga. Por ejemplo, la siguiente llamada produce un vector de longitud dos:

expr <- expr(g(a + b + c + d + e + f + g + h + i + j + k + l + 
  m + n + o + p + q + r + s + t + u + v + w + x + y + z))

deparse(expr)

¿Qué hace expr_text() en su lugar?

pairwise.t.test() asume que deparse() siempre devuelve un vector de un carácter de longitud. ¿Puedes construir una entrada que viole esta expectativa? ¿Lo que sucede?

18.5 Walking AST con funciones recursivas

Para concluir el capítulo, voy a utilizar todo lo que ha aprendido sobre los AST para resolver problemas más complicados. La inspiración proviene del paquete de herramientas de código base, que proporciona dos funciones interesantes:

findGlobals() localiza todas las variables globales utilizadas por una función. Esto puede ser útil si desea verificar que su función no dependa inadvertidamente de variables definidas en su entorno principal.
checkUsage() comprueba una variedad de problemas comunes, incluidas las variables locales no utilizadas, los parámetros no utilizados y el uso de coincidencias de argumentos parciales.

Obtener todos los detalles de estas funciones correctamente es complicado, por lo que no desarrollaremos completamente las ideas. En su lugar, nos centraremos en la gran idea subyacente: la recursividad en el AST. Las funciones recursivas se ajustan naturalmente a las estructuras de datos de tipo árbol porque una función recursiva se compone de dos partes que corresponden a las dos partes del árbol:

El caso recursivo maneja los nodos en el árbol. Por lo general, hará algo con cada hijo de un nodo, por lo general llamando a la función recursiva nuevamente, y luego combinará los resultados nuevamente. Para las expresiones, deberá manejar llamadas y listas de pares (argumentos de función).
El caso base maneja las hojas del árbol. Los casos base aseguran que la función eventualmente termine, resolviendo directamente los casos más simples. Para las expresiones, debe manejar símbolos y constantes en el caso base.

Para que este patrón sea más fácil de ver, necesitaremos dos funciones auxiliares. Primero definimos expr_type() que devolverá “constante” para constante, “símbolo” para símbolos, “call”, para llamadas, “pairlist” para listas de pares y el “tipo” de cualquier otra cosa:

expr_type <- function(x) {
  if (rlang::is_syntactic_literal(x)) {
    "constant"
  } else if (is.symbol(x)) {
    "symbol"
  } else if (is.call(x)) {
    "call"
  } else if (is.pairlist(x)) {
    "pairlist"
  } else {
    typeof(x)
  }
}

expr_type(expr("a"))
#> [1] "constant"
expr_type(expr(x))
#> [1] "symbol"
expr_type(expr(f(1, 2)))
#> [1] "call"

Combinaremos esto con un contenedor alrededor de la función de cambio:

switch_expr <- function(x, ...) {
  switch(expr_type(x),
    ...,
    stop("Don't know how to handle type ", typeof(x), call. = FALSE)
  )
}

Con estas dos funciones en la mano, podemos escribir una plantilla básica para cualquier función que recorra el AST usando switch() (Sección 5.2.3):

recurse_call <- function(x) {
  switch_expr(x,
    # Casos base
    symbol = ,
    constant = ,

    # Casos recursivos
    call = ,
    pairlist =
  )
}

Por lo general, resolver el caso base es fácil, así que lo haremos primero y luego verificaremos los resultados. Los casos recursivos son más complicados y, a menudo, requerirán alguna programación funcional.

18.5.1 Encontrar F y T

Comenzaremos con una función que determina si otra función usa las abreviaturas lógicas T y F porque usarlas a menudo se considera una mala práctica de codificación. Nuestro objetivo es devolver TRUE si la entrada contiene una abreviatura lógica y FALSE en caso contrario.

Primero encontremos el tipo de T versus TRUE:

expr_type(expr(TRUE))
#> [1] "constant"

expr_type(expr(T))
#> [1] "symbol"

TRUE se analiza como un vector lógico de longitud uno, mientras que T se analiza como un nombre. Esto nos dice cómo escribir nuestros casos base para la función recursiva: una constante nunca es una abreviatura lógica, y un símbolo es una abreviatura si es “F” o “T”:

logical_abbr_rec <- function(x) {
  switch_expr(x,
    constant = FALSE,
    symbol = as_string(x) %in% c("F", "T")
  )
}

logical_abbr_rec(expr(TRUE))
#> [1] FALSE
logical_abbr_rec(expr(T))
#> [1] TRUE

He escrito la función logical_abbr_rec() asumiendo que la entrada será una expresión, ya que esto simplificará la operación recursiva. Sin embargo, cuando se escribe una función recursiva, es común escribir un contenedor que proporciona valores predeterminados o hace que la función sea un poco más fácil de usar. Aquí normalmente crearemos un envoltorio que cita su entrada (aprenderemos más sobre eso en el próximo capítulo), por lo que no necesitamos usar expr() cada vez.

logical_abbr <- function(x) {
  logical_abbr_rec(enexpr(x))
}

logical_abbr(T)
#> [1] TRUE
logical_abbr(FALSE)
#> [1] FALSE

A continuación, debemos implementar los casos recursivos. Aquí queremos hacer lo mismo para las llamadas y para las listas de pares: aplique recursivamente la función a cada subcomponente y devuelva TRUE si algún subcomponente contiene una abreviatura lógica. Esto se facilita con purrr::some(), que itera sobre una lista y devuelve TRUE si la función de predicado es verdadera para cualquier elemento.

logical_abbr_rec <- function(x) {
  switch_expr(x,
    # Casos base
    constant = FALSE,
    symbol = as_string(x) %in% c("F", "T"),

    # Casos recursivos
    call = ,
    pairlist = purrr::some(x, logical_abbr_rec)
  )
}

logical_abbr(mean(x, na.rm = T))
#> [1] TRUE
logical_abbr(function(x, na.rm = T) FALSE)
#> [1] TRUE

18.5.2 Encontrar todas las variables creadas por asignación

logical_abbr() es relativamente simple: solo devuelve un solo TRUE o FALSE. La siguiente tarea, enumerar todas las variables creadas por asignación, es un poco más complicada. Comenzaremos de manera simple y luego haremos que la función sea progresivamente más rigurosa.

Comenzamos mirando el AST para la asignación:

ast(x <- 10)
#> █─`<-` 
#> ├─x 
#> └─10

La asignación es un objeto de llamada donde el primer elemento es el símbolo <-, el segundo es el nombre de la variable y el tercero es el valor a asignar.

A continuación, debemos decidir qué estructura de datos vamos a utilizar para los resultados. Aquí creo que será más fácil si devolvemos un vector de caracteres. Si devolvemos símbolos, necesitaremos usar una list() y eso hace las cosas un poco más complicadas.

Con eso en la mano, podemos comenzar implementando los casos base y proporcionando un envoltorio útil alrededor de la función recursiva. Aquí los casos base son sencillos porque sabemos que ni un símbolo ni una constante representan una asignación.

find_assign_rec <- function(x) {
  switch_expr(x,
    constant = ,
    symbol = character()
  )
}
find_assign <- function(x) find_assign_rec(enexpr(x))

find_assign("x")
#> character(0)
find_assign(x)
#> character(0)

A continuación implementamos los casos recursivos. Esto es más fácil gracias a una función que debería existir en purrr, pero actualmente no existe. flat_map_chr() espera que .f devuelva un vector de caracteres de longitud arbitraria y aplana todos los resultados en un solo vector de caracteres.

flat_map_chr <- function(.x, .f, ...) {
  purrr::flatten_chr(purrr::map(.x, .f, ...))
}

flat_map_chr(letters[1:3], ~ rep(., sample(3, 1)))
#> [1] "a" "b" "b" "b" "c" "c" "c"

El caso recursivo para las listas de pares es sencillo: iteramos sobre cada elemento de la lista de pares (es decir, cada argumento de función) y combinamos los resultados. El caso de las llamadas es un poco más complejo: si se trata de una llamada a <- entonces deberíamos devolver el segundo elemento de la llamada:

find_assign_rec <- function(x) {
  switch_expr(x,
    # Casos base
    constant = ,
    symbol = character(),

    # Casos recursivos
    pairlist = flat_map_chr(as.list(x), find_assign_rec),
    call = {
      if (is_call(x, "<-")) {
        as_string(x[[2]])
      } else {
        flat_map_chr(as.list(x), find_assign_rec)
      }
    }
  )
}

find_assign(a <- 1)
#> [1] "a"
find_assign({
  a <- 1
  {
    b <- 2
  }
})
#> [1] "a" "b"

Ahora necesitamos hacer que nuestra función sea más robusta al presentar ejemplos destinados a romperla. ¿Qué sucede cuando asignamos a la misma variable varias veces?

find_assign({
  a <- 1
  a <- 2
})
#> [1] "a" "a"

Es más fácil arreglar esto en el nivel de la función contenedora:

find_assign <- function(x) unique(find_assign_rec(enexpr(x)))

find_assign({
  a <- 1
  a <- 2
})
#> [1] "a"

¿Qué sucede si tenemos llamadas anidadas a <-? Actualmente solo devolvemos el primero. Eso es porque cuando ocurre <- terminamos inmediatamente la recursividad.

find_assign({
  a <- b <- c <- 1
})
#> [1] "a"

En su lugar, tenemos que adoptar un enfoque más riguroso. Creo que es mejor mantener la función recursiva enfocada en la estructura de árbol, así que voy a extraer find_assign_call() en una función separada.

find_assign_call <- function(x) {
  if (is_call(x, "<-") && is_symbol(x[[2]])) {
    lhs <- as_string(x[[2]])
    children <- as.list(x)[-1]
  } else {
    lhs <- character()
    children <- as.list(x)
  }

  c(lhs, flat_map_chr(children, find_assign_rec))
}

find_assign_rec <- function(x) {
  switch_expr(x,
    # Casos base
    constant = ,
    symbol = character(),

    # Casos recursivos
    pairlist = flat_map_chr(x, find_assign_rec),
    call = find_assign_call(x)
  )
}

find_assign(a <- b <- c <- 1)
#> [1] "a" "b" "c"
find_assign(system.time(x <- print(y <- 5)))
#> [1] "x" "y"

La versión completa de esta función es bastante complicada, es importante recordar que la escribimos trabajando a nuestro modo escribiendo componentes simples.

18.5.3 Ejercicios

logical_abbr() devuelve TRUE para T(1, 2, 3). ¿Cómo podrías modificar logical_abbr_rec() para que ignore las llamadas a funciones que usan T o F?
logical_abbr() trabaja con expresiones. Actualmente falla cuando le das una función. ¿Por qué? ¿Cómo podrías modificar logical_abbr() para que funcione? ¿Sobre qué componentes de una función necesitará recurrir?
```
logical_abbr(function(x = TRUE) {
  g(x + T)
})
```
Modifique find_assign para detectar también la asignación usando funciones de reemplazo, es decir, names(x) <- y.
Escriba una función que extraiga todas las llamadas a una función específica.

18.6 Estructuras de datos especializadas

Hay dos estructuras de datos y un símbolo especial que debemos cubrir en aras de la exhaustividad. No suelen ser importantes en la práctica.

18.6.1 Listas de pares

Las listas de pares son un remanente del pasado de R y han sido reemplazadas por listas en casi todas partes. El único lugar donde es probable que vea listas de pares en R⁴ es cuando trabaja con llamadas a la función función, ya que los argumentos formales de una función se almacenan en una lista de pares:

f <- expr(function(x, y = 10) x + y)

args <- f[[2]]
args
#> $x
#> 
#> 
#> $y
#> [1] 10
typeof(args)
#> [1] "pairlist"

Afortunadamente, cada vez que encuentre una lista de pares, puede tratarla como una lista normal:

pl <- pairlist(x = 1, y = 2)
length(pl)
#> [1] 2
pl$x
#> [1] 1

Detrás de escena, las listas de pares se implementan utilizando una estructura de datos diferente, una lista vinculada en lugar de una matriz. Eso hace que subdividir una lista de pares sea mucho más lento que subdividir una lista, pero esto tiene poco impacto práctico.

18.6.2 Argumentos faltantes

El símbolo especial que necesita un poco más de discusión es el símbolo vacío, que se usa para representar argumentos faltantes (¡no valores faltantes!). Solo necesita preocuparse por el símbolo faltante si está creando funciones mediante programación con argumentos faltantes; volveremos a eso en la Sección 19.4.3.

Puedes crear un símbolo vacío con missing_arg() (o expr()):

missing_arg()
typeof(missing_arg())
#> [1] "symbol"

Un símbolo vacío no imprime nada, así que puedes comprobar si tienes uno con rlang::is_missing():

is_missing(missing_arg())
#> [1] TRUE

Los encontrará en la naturaleza en funciones formales:

f <- expr(function(x, y = 10) x + y)
args <- f[[2]]
is_missing(args[[1]])
#> [1] TRUE

Esto es particularmente importante para ... que siempre está asociado con un símbolo vacío:

f <- expr(function(...) list(...))
args <- f[[2]]
is_missing(args[[1]])
#> [1] TRUE

El símbolo vacío tiene una propiedad peculiar: si lo vincula a una variable, luego accede a esa variable, obtendrá un error:

m <- missing_arg()
m
#> Error in eval(expr, envir, enclos): argument "m" is missing, with no default

¡Pero no lo hará si lo almacena dentro de otra estructura de datos!

ms <- list(missing_arg(), missing_arg())
ms[[1]]

Si necesita preservar la falta de una variable, rlang::maybe_missing() suele ser útil. Le permite referirse a una variable potencialmente faltante sin desencadenar el error. Consulte la documentación para casos de uso y más detalles.

18.6.3 Vectores de expresión

Finalmente, necesitamos discutir brevemente el vector de expresión. Los vectores de expresión solo son producidos por dos funciones base: expression() y parse():

exp1 <- parse(text = c("
x <- 4
x
"))
exp2 <- expression(x <- 4, x)

typeof(exp1)
#> [1] "expression"
typeof(exp2)
#> [1] "expression"

exp1
#> expression(x <- 4, x)
exp2
#> expression(x <- 4, x)

Al igual que las llamadas y las listas de pares, los vectores de expresión se comportan como listas:

length(exp1)
#> [1] 2
exp1[[1]]
#> x <- 4

Conceptualmente, un vector de expresión es solo una lista de expresiones. La única diferencia es que llamar a eval() en una expresión evalúa cada expresión individual. No creo que esta ventaja merezca la introducción de una nueva estructura de datos, por lo que en lugar de vectores de expresión, solo uso listas de expresiones.

Para un código más complejo, también puede usar el visor de árboles de RStudio, que no obedece a las mismas convenciones gráficas, pero le permite explorar de forma interactiva grandes AST. Pruébelo con View(expr(f(x, "y", 1))).↩︎
Los nombres de las funciones sin prefijo no son sintácticos, por lo que los rodeo con ``, como en la Sección 2.2.1.↩︎
Curiosamente, también puede ser un número, como en la expresión 3(). Pero esta llamada siempre fallará en la evaluación porque un número no es una función.↩︎
Si está trabajando en C, encontrará listas de pares con más frecuencia. Por ejemplo, los objetos de llamada también se implementan mediante listas de pares.↩︎