4  Subconjunto

4.1 Introducción

Los operadores de subconjuntos de R son rápidos y potentes. Dominarlos le permite realizar operaciones complejas de manera sucinta de una manera que pocos otros idiomas pueden igualar. La creación de subconjuntos en R es fácil de aprender pero difícil de dominar porque necesita interiorizar una serie de conceptos interrelacionados:

• Hay seis formas de crear subconjuntos de vectores atómicos.

• Hay tres operadores de subconjuntos, [[, [ y $.

• Los operadores de creación de subconjuntos interactúan de manera diferente con diferentes tipos de vectores (por ejemplo, vectores atómicos, listas, factores, matrices y data frames).

• La creación de subconjuntos se puede combinar con la asignación.

La creación de subconjuntos es un complemento natural de str(). Mientras que str() le muestra todas las piezas de cualquier objeto (su estructura), la creación de subconjuntos le permite extraer las piezas que le interesan. Para objetos grandes y complejos, recomiendo usar el RStudio Viewer interactivo, que puedes activar con View(my_object).

Prueba

Responda este breve cuestionario para determinar si necesita leer este capítulo. Si las respuestas le vienen a la mente rápidamente, puede saltarse cómodamente este capítulo. Comprueba tus respuestas en la Sección 4.6.

1. ¿Cuál es el resultado de subdividir un vector con enteros positivos, enteros negativos, un vector lógico o un vector de caracteres?

2. ¿Cuál es la diferencia entre [, [[ y $ cuando se aplica a una lista?

3. ¿Cuándo debería usar drop = FALSE?

4. Si x es una matriz, ¿qué hace x[] <- 0? ¿En qué se diferencia de x <- 0?

5. ¿Cómo puede usar un vector con nombre para volver a etiquetar variables categóricas?

Estructura

• La Sección 4.2 comienza enseñándote acerca de [. Aprenderá las seis formas de crear subconjuntos de vectores atómicos. Luego aprenderá cómo actúan esas seis formas cuando se usan para crear subconjuntos de listas, matrices y data frames.

• La Sección 4.3 amplía su conocimiento de los operadores de subconjuntos para incluir [[ y $ y se centra en los principios importantes de simplificar frente a preservar.

• La Sección 4.4 aprenderá el arte de la subasignación, que combina subconjuntos y asignación para modificar partes de un objeto.

• La Sección 4.5 llo guía a través de ocho aplicaciones importantes, pero no obvias, de subconjuntos para resolver problemas que a menudo encuentra en el análisis de datos.

4.2 Selección de varios elementos

Utilice [ para seleccionar cualquier número de elementos de un vector. Para ilustrar, aplicaré [ a vectores atómicos 1D, y luego mostraré cómo esto se generaliza a objetos más complejos y más dimensiones.

4.2.1 Vectores atómicos

Exploremos los diferentes tipos de subconjuntos con un vector simple, x.

x <- c(2.1, 4.2, 3.3, 5.4)

Tenga en cuenta que el número después del punto decimal representa la posición original en el vector.

Hay seis cosas que puede usar para crear subconjuntos de un vector:

• Los enteros positivos devuelven elementos en las posiciones especificadas:

  x[c(3, 1)]
  #> [1] 3.3 2.1
  x[order(x)]
  #> [1] 2.1 3.3 4.2 5.4
  
  # Los índices duplicados duplicarán los valores
  x[c(1, 1)]
  #> [1] 2.1 2.1
  
  # Los números reales se truncan silenciosamente a enteros
  x[c(2.1, 2.9)]
  #> [1] 4.2 4.2

• Los enteros negativos excluyen elementos en las posiciones especificadas:

  x[-c(3, 1)]
  #> [1] 4.2 5.4

  Tenga en cuenta que no puede mezclar números enteros positivos y negativos en un solo subconjunto:

  x[c(-1, 2)]
  #> Error in x[c(-1, 2)]: only 0's may be mixed with negative subscripts

• Los vectores lógicos seleccionan elementos donde el valor lógico correspondiente es TRUE. Este es probablemente el tipo de subconjunto más útil porque puede escribir una expresión que usa un vector lógico:

  x[c(TRUE, TRUE, FALSE, FALSE)]
  #> [1] 2.1 4.2
  x[x > 3]
  #> [1] 4.2 3.3 5.4

  En x[y], ¿qué sucede si x e y tienen longitudes diferentes? El comportamiento está controlado por las reglas de reciclaje, donde el más corto de los dos se recicla al largo del más largo. Esto es conveniente y fácil de entender cuando uno de x e y tiene la longitud uno, pero recomiendo evitar el reciclaje para otras longitudes porque las reglas se aplican de manera inconsistente en la base R.

  x[c(TRUE, FALSE)]
  #> [1] 2.1 3.3
  # Equivalent to
  x[c(TRUE, FALSE, TRUE, FALSE)]
  #> [1] 2.1 3.3

  Tenga en cuenta que un valor faltante en el índice siempre produce un valor faltante en la salida:

  x[c(TRUE, TRUE, NA, FALSE)]
  #> [1] 2.1 4.2  NA

• Nada devuelve el vector original. Esto no es útil para vectores 1D, pero, como verá en breve, es muy útil para matrices, data frames y arreglos. También puede ser útil junto con la asignación.

  x[]
  #> [1] 2.1 4.2 3.3 5.4

• Zero devuelve un vector de longitud cero. Esto no es algo que normalmente haga a propósito, pero puede ser útil para generar datos de prueba.

  x[0]
  #> numeric(0)

• Si el vector tiene nombre, también puede usar vectores de caracteres para devolver elementos con nombres coincidentes.

  (y <- setNames(x, letters[1:4]))
  #>   a   b   c   d 
  #> 2.1 4.2 3.3 5.4
  y[c("d", "c", "a")]
  #>   d   c   a 
  #> 5.4 3.3 2.1
  
  # Al igual que los índices enteros, puede repetir índices
  y[c("a", "a", "a")]
  #>   a   a   a 
  #> 2.1 2.1 2.1
  
  # Al crear un subconjunto con [, los nombres siempre coinciden exactamente
  z <- c(abc = 1, def = 2)
  z[c("a", "d")]
  #> <NA> <NA> 
  #>   NA   NA

NB: Los factores no se tratan de manera especial cuando se subdividen. Esto significa que la creación de subconjuntos utilizará el vector entero subyacente, no los niveles de caracteres. Esto suele ser inesperado, por lo que debe evitar subconjuntos con factores:

y[factor("b")]
#>   a 
#> 2.1

4.2.2 Listas

La creación de subconjuntos de una lista funciona de la misma manera que la creación de subconjuntos de un vector atómico. Usar [ siempre devuelve una lista; [[ y $, como se describe en la Sección 4.3, le permiten extraer elementos de una lista.

4.2.3 Matrices y arreglos

Puede crear subconjuntos de estructuras de dimensiones superiores de tres maneras:

• Con múltiples vectores.
• Con un solo vector.
• Con una matriz.

La forma más común de crear subconjuntos de matrices (2D) y arreglos (>2D) es una generalización simple de subconjuntos 1D: proporcione un índice 1D para cada dimensión, separados por una coma. El subconjunto en blanco ahora es útil porque le permite mantener todas las filas o todas las columnas.

a <- matrix(1:9, nrow = 3)
colnames(a) <- c("A", "B", "C")
a[1:2, ]
#>      A B C
#> [1,] 1 4 7
#> [2,] 2 5 8
a[c(TRUE, FALSE, TRUE), c("B", "A")]
#>      B A
#> [1,] 4 1
#> [2,] 6 3
a[0, -2]
#>      A C

Por defecto, [ simplifica los resultados a la dimensionalidad más baja posible. Por ejemplo, las dos expresiones siguientes devuelven vectores 1D. Aprenderá cómo evitar “reducir” el número de dimensiones en la Sección 4.2.5:

a[1, ]
#> A B C 
#> 1 4 7
a[1, 1]
#> A 
#> 1

Debido a que tanto las matrices como los arreglos son solo vectores con atributos especiales, puede crear subconjuntos con un solo vector, como si fueran un vector 1D. Tenga en cuenta que las matrices en R se almacenan en orden de columna principal:

vals <- outer(1:5, 1:5, FUN = "paste", sep = ",")
vals
#>      [,1]  [,2]  [,3]  [,4]  [,5] 
#> [1,] "1,1" "1,2" "1,3" "1,4" "1,5"
#> [2,] "2,1" "2,2" "2,3" "2,4" "2,5"
#> [3,] "3,1" "3,2" "3,3" "3,4" "3,5"
#> [4,] "4,1" "4,2" "4,3" "4,4" "4,5"
#> [5,] "5,1" "5,2" "5,3" "5,4" "5,5"

vals[c(4, 15)]
#> [1] "4,1" "5,3"

También puede crear subconjuntos de estructuras de datos de mayor dimensión con una matriz de enteros (o, si se nombra, una matriz de caracteres). Cada fila de la matriz especifica la ubicación de un valor y cada columna corresponde a una dimensión de la matriz. Esto significa que puede usar una matriz de 2 columnas para crear un subconjunto de una matriz, una matriz de 3 columnas para crear un subconjunto de una matriz 3D, etc. El resultado es un vector de valores:

select <- matrix(ncol = 2, byrow = TRUE, c(
  1, 1,
  3, 1,
  2, 4
))
vals[select]
#> [1] "1,1" "3,1" "2,4"

4.2.4 Data frames y tibbles

Data frames tienen las características tanto de listas como de matrices:

• Cuando se subdividen con un solo índice, se comportan como listas e indexan las columnas, por lo que df[1:2] selecciona las dos primeras columnas.

• Al crear subconjuntos con dos índices, se comportan como matrices, por lo que df[1:3, ] selecciona las primeras tres filas (y todas las columnas)¹.

df <- data.frame(x = 1:3, y = 3:1, z = letters[1:3])

df[df$x == 2, ]
#>   x y z
#> 2 2 2 b
df[c(1, 3), ]
#>   x y z
#> 1 1 3 a
#> 3 3 1 c

# Hay dos formas de seleccionar columnas de un data frame
# Como una lista
df[c("x", "z")]
#>   x z
#> 1 1 a
#> 2 2 b
#> 3 3 c
# Como una matriz
df[, c("x", "z")]
#>   x z
#> 1 1 a
#> 2 2 b
#> 3 3 c

# Hay una diferencia importante si selecciona una sola 
# columna: el subconjunto de la matriz se simplifica de forma predeterminada, el 
# subconjunto de la lista no
str(df["x"])
#> 'data.frame':    3 obs. of  1 variable:
#>  $ x: int  1 2 3
str(df[, "x"])
#>  int [1:3] 1 2 3

Subdividir un tibble con [ siempre devuelve un tibble:

df <- tibble::tibble(x = 1:3, y = 3:1, z = letters[1:3])

str(df["x"])
#> tibble [3 × 1] (S3: tbl_df/tbl/data.frame)
#>  $ x: int [1:3] 1 2 3
str(df[, "x"])
#> tibble [3 × 1] (S3: tbl_df/tbl/data.frame)
#>  $ x: int [1:3] 1 2 3

4.2.5 Preservando la dimensionalidad

De forma predeterminada, subdividir una matriz o data frame con un solo número, un solo nombre o un vector lógico que contenga un solo TRUE simplificará la salida devuelta, es decir, devolverá un objeto con menor dimensionalidad. Para conservar la dimensionalidad original, debe usar drop = FALSE.

• Para matrices y arreglos, se eliminarán todas las dimensiones con longitud 1:

  a <- matrix(1:4, nrow = 2)
  str(a[1, ])
  #>  int [1:2] 1 3
  
  str(a[1, , drop = FALSE])
  #>  int [1, 1:2] 1 3

• Data frames con una sola columna devolverán solo el contenido de esa columna:

  df <- data.frame(a = 1:2, b = 1:2)
  str(df[, "a"])
  #>  int [1:2] 1 2
  
  str(df[, "a", drop = FALSE])
  #> 'data.frame':    2 obs. of  1 variable:
  #>  $ a: int  1 2

El comportamiento predeterminado drop = TRUE es una fuente común de errores en las funciones: verifica su código con un data frame o matriz con varias columnas, y funciona. Seis meses después, usted (u otra persona) lo usa con un data frame de una sola columna y falla con un error desconcertante. Al escribir funciones, acostúmbrese a usar siempre drop = FALSE al subdividir un objeto 2D. Por esta razón, los tibbles tienen por defecto drop = FALSE, y [ siempre devuelve otro tibble.

El subconjunto de factores también tiene un argumento drop, pero su significado es bastante diferente. Controla si se conservan o no los niveles (en lugar de las dimensiones), y su valor predeterminado es FALSE. Si encuentra que está usando drop = TRUE mucho, a menudo es una señal de que debería estar usando un vector de caracteres en lugar de un factor.

z <- factor(c("a", "b"))
z[1]
#> [1] a
#> Levels: a b
z[1, drop = TRUE]
#> [1] a
#> Levels: a

4.2.6 Ejercicios

1. Solucione cada uno de los siguientes errores comunes de creación de subconjuntos de data frames:

   mtcars[mtcars$cyl = 4, ]
   mtcars[-1:4, ]
   mtcars[mtcars$cyl <= 5]
   mtcars[mtcars$cyl == 4 | 6, ]

2. ¿Por qué el siguiente código arroja cinco valores faltantes? (Pista: ¿por qué es diferente de x[NA_real_]?)

   x <- 1:5
   x[NA]
   #> [1] NA NA NA NA NA

3. ¿Qué devuelve upper.tri()? ¿Cómo funciona el subconjunto de una matriz con él? ¿Necesitamos reglas adicionales de creación de subconjuntos para describir su comportamiento?

   x <- outer(1:5, 1:5, FUN = "*")
   x[upper.tri(x)]

4. ¿Por qué mtcars[1:20] devuelve un error? ¿En qué se diferencia de los mtcars[1:20, ] similares?

5. Implemente su propia función que extraiga las entradas diagonales de una matriz (debería comportarse como diag(x) donde x es una matriz).

6. ¿Qué hace df[is.na(df)] <- 0? ¿Como funciona?

4.3 Selección de un solo elemento

Hay otros dos operadores de subconjuntos: [[ y $. [[ se usa para extraer elementos individuales, mientras que x$y es una abreviatura útil para x[["y"]].

4.3.1 [[

[[ es más importante cuando se trabaja con listas porque subdividir una lista con [ siempre devuelve una lista más pequeña. Para ayudar a que esto sea más fácil de entender, podemos usar una metáfora:

Si la lista x es un tren que transporta objetos, entonces x[[5]] es el objeto en el vagón 5; x[4:6] es un tren de vagones 4-6.

— @RLangTip, https://twitter.com/RLangTip/status/268375867468681216

Usemos esta metáfora para hacer una lista simple:

x <- list(1:3, "a", 4:6)

Al extraer un solo elemento, tiene dos opciones: puede crear un tren más pequeño, es decir, menos vagones, o puede extraer el contenido de un vagón en particular. Esta es la diferencia entre [ y [[:

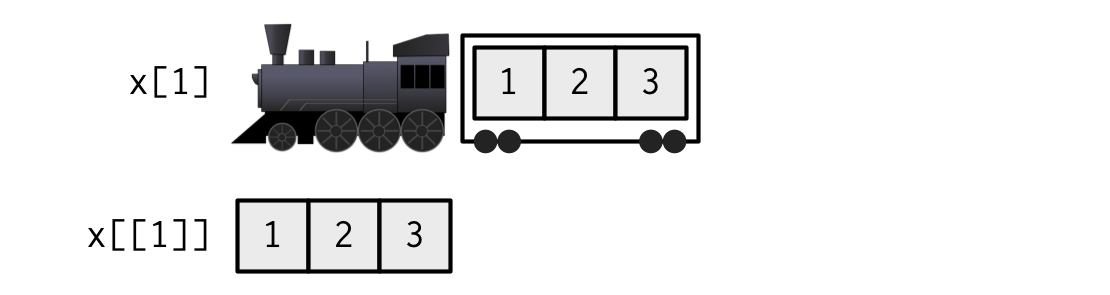
Al extraer elementos múltiples (¡o incluso cero!), debe hacer un tren más pequeño:

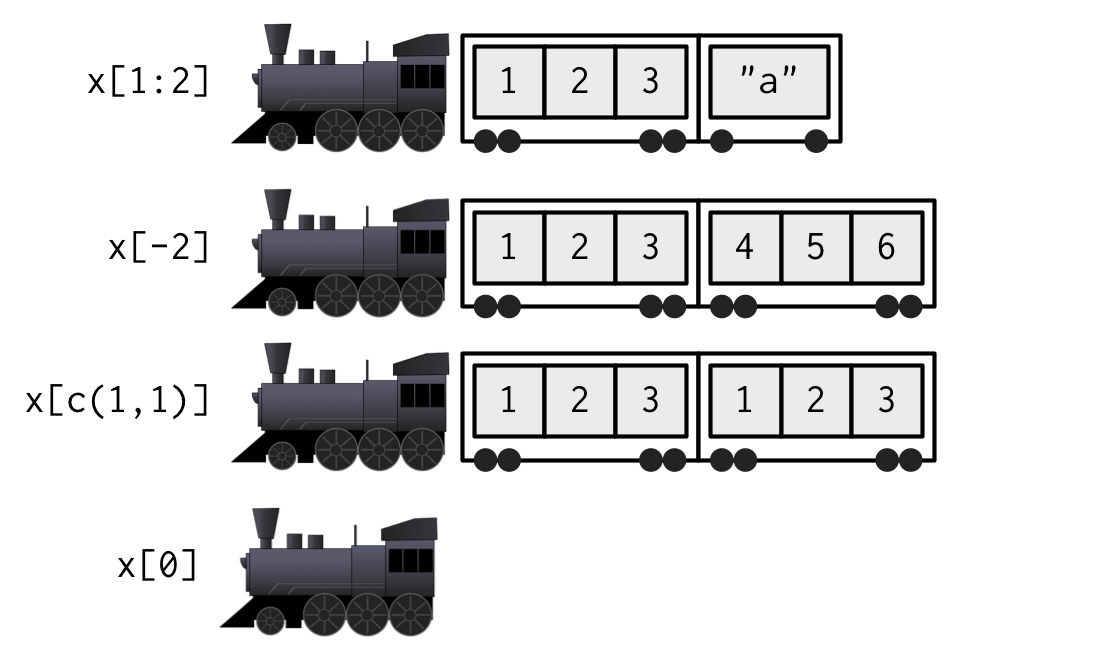
Debido a que [[ solo puede devolver un solo elemento, debe usarlo con un solo entero positivo o una sola cadena. Si usa un vector con [[, se subdividirá recursivamente, es decir, x[[c(1, 2)]] es equivalente a x[[1]][[2]]. Esta es una característica peculiar que pocos conocen, así que recomiendo evitarla en favor de purrr::pluck(), sobre la cual aprenderá en la Sección 4.3.3.

Si bien debe usar [[ cuando trabaja con listas, también recomendaría usarlo con vectores atómicos siempre que desee extraer un solo valor. Por ejemplo, en lugar de escribir:

for (i in 2:length(x)) {
  out[i] <- fun(x[i], out[i - 1])
}

Es mejor escribir:

for (i in 2:length(x)) {
  out[[i]] <- fun(x[[i]], out[[i - 1]])
}

Si lo hace, refuerza la expectativa de que está recibiendo y estableciendo valores individuales.

4.3.2 $

$ es un operador abreviado: x$y es aproximadamente equivalente a x[["y", exact = FALSE]]. A menudo se usa para acceder a variables en un data frame, como en mtcars$cyl o diamonds$carat. Un error común con $ es usarlo cuando tienes el nombre de una columna almacenada en una variable:

var <- "cyl"
# No funciona - mtcars$var traducido a mtcars[["var"]]
mtcars$var
#> NULL

# En su lugar use [[
mtcars[[var]]
#>  [1] 6 6 4 6 8 6 8 4 4 6 6 8 8 8 8 8 8 4 4 4 4 8 8 8 8 4 4 4 8 6 8 4

La única diferencia importante entre $ y [[ es que $ automáticamente hace (de izquierda a derecha) coincidencias parciales sin previo aviso:

x <- list(abc = 1)
x$a
#> [1] 1
x[["a"]]
#> NULL

Para ayudar a evitar este comportamiento, recomiendo configurar la opción global warnPartialMatchDollar en TRUE:

options(warnPartialMatchDollar = TRUE)
x$a
#> Warning in x$a: partial match of 'a' to 'abc'
#> [1] 1

(Para data frames, también puede evitar este problema usando tibbles, que nunca hacen coincidencias parciales.)

4.3.3 Índices faltantes y fuera de los límites

Es útil comprender lo que sucede con [[ cuando usa un índice “no válido”. La siguiente tabla resume lo que sucede cuando crea un subconjunto de un vector lógico, una lista y un NULL con un objeto de longitud cero (como NULL o logical()), valores fuera de los límites (OOB) o un valor faltante (por ejemplo, NA_integer_) con [[. Cada celda muestra el resultado de dividir la estructura de datos nombrada en la fila por el tipo de índice descrito en la columna. Solo he mostrado los resultados para vectores lógicos, pero otros vectores atómicos se comportan de manera similar, devolviendo elementos del mismo tipo (NB: int = entero; chr = carácter).

row[[col]]	Longitud cero	OOB (int)	OOB (chr)	Faltante
Atómico	Error	Error	Error	Error
Lista	Error	Error	NULL	NULL
NULL	NULL	NULL	NULL	NULL

Si se nombra el vector que se indexa, los nombres de los componentes OOB, faltantes o NULL serán <NA>.

Las inconsistencias en la tabla anterior llevaron al desarrollo de purrr::pluck() y purrr::chuck(). Cuando falta el elemento, pluck() siempre devuelve NULL (o el valor del argumento .default) y chuck() siempre arroja un error. El comportamiento de pluck() lo hace ideal para la indexación en estructuras de datos profundamente anidadas donde el componente que desea puede no existir (como es común cuando se trabaja con datos JSON de API web). pluck() también te permite mezclar índices enteros y de caracteres, y proporciona un valor predeterminado alternativo si un elemento no existe:

x <- list(
  a = list(1, 2, 3),
  b = list(3, 4, 5)
)

purrr::pluck(x, "a", 1)
#> [1] 1

purrr::pluck(x, "c", 1)
#> NULL

purrr::pluck(x, "c", 1, .default = NA)
#> [1] NA

4.3.4 @ y slot()

Hay dos operadores de subconjuntos adicionales, que son necesarios para los objetos de S4: @ (equivalente a $) y slot() (equivalente a [[). @ es más restrictivo que $ ya que devolverá un error si la ranura no existe. Estos se describen con más detalle en el Capítulo 15.

4.3.5 Ejercicios

1. Piense en tantas formas como sea posible para extraer el tercer valor de la variable cyl en el conjunto de datos mtcars.

2. Dado un modelo lineal, por ejemplo, mod <- lm(mpg ~ wt, data = mtcars), extraiga los grados de libertad residuales. Luego extraiga la R al cuadrado del resumen del modelo (summary (mod))

4.4 Subconjunto y asignación

Todos los operadores de subconjunto se pueden combinar con la asignación para modificar los valores seleccionados de un vector de entrada: esto se denomina subasignación. La forma básica es x[i] <- valor:

x <- 1:5
x[c(1, 2)] <- c(101, 102)
x
#> [1] 101 102   3   4   5

Te recomiendo que te asegures de que length(valor) sea lo mismo que length(x[i]), y que i sea único. Esto se debe a que, si bien R reciclará si es necesario, esas reglas son complejas (particularmente si i contiene valores faltantes o duplicados) y pueden causar problemas.

Con las listas, puede usar x[[i]] <- NULL para eliminar un componente. Para agregar un literal NULL, use x[i] <- list(NULL):

x <- list(a = 1, b = 2)
x[["b"]] <- NULL
str(x)
#> List of 1
#>  $ a: num 1

y <- list(a = 1, b = 2)
y["b"] <- list(NULL)
str(y)
#> List of 2
#>  $ a: num 1
#>  $ b: NULL

La creación de subconjuntos sin nada puede ser útil con la asignación porque conserva la estructura del objeto original. Compara las siguientes dos expresiones. En el primero, mtcars sigue siendo un data frame porque solo está cambiando el contenido de mtcars, no mtcars en sí. En el segundo, mtcars se convierte en una lista porque está cambiando el objeto al que está vinculado.

mtcars[] <- lapply(mtcars, as.integer)
is.data.frame(mtcars)
#> [1] TRUE

mtcars <- lapply(mtcars, as.integer)
is.data.frame(mtcars)
#> [1] FALSE

4.5 Aplicaciones

Los principios descritos anteriormente tienen una amplia variedad de aplicaciones útiles. A continuación se describen algunos de los más importantes. Si bien muchos de los principios básicos de creación de subconjuntos ya se han incorporado en funciones como subset(), merge() y dplyr::arrange(), será valioso comprender mejor cómo se han implementado esos principios. cuando se encuentra con situaciones en las que las funciones que necesita no existen.

4.5.1 Tablas de búsqueda (subconjunto de caracteres)

La coincidencia de caracteres es una forma poderosa de crear tablas de búsqueda. Digamos que quieres convertir abreviaturas:

x <- c("m", "f", "u", "f", "f", "m", "m")
lookup <- c(m = "Male", f = "Female", u = NA)
lookup[x]
#>        m        f        u        f        f        m        m 
#>   "Male" "Female"       NA "Female" "Female"   "Male"   "Male"

Tenga en cuenta que si no quiere nombres en el resultado, use unname() para eliminarlos.

unname(lookup[x])
#> [1] "Male"   "Female" NA       "Female" "Female" "Male"   "Male"

4.5.2 Coincidencia y fusión a mano (subconjunto de enteros)

También puede tener tablas de búsqueda más complicadas con múltiples columnas de información. Por ejemplo, supongamos que tenemos un vector de grados enteros y una tabla que describe sus propiedades:

grades <- c(1, 2, 2, 3, 1)

info <- data.frame(
  grade = 3:1,
  desc = c("Excellent", "Good", "Poor"),
  fail = c(F, F, T)
)

Entonces, digamos que queremos duplicar la tabla info para que tengamos una fila para cada valor en grade. Una forma elegante de hacer esto es combinando match() y un subconjunto de enteros (match(aguja, pajar) devuelve la posición donde se encuentra cada aguja en el pajar).

id <- match(grades, info$grade)
id
#> [1] 3 2 2 1 3
info[id, ]
#>     grade      desc  fail
#> 3       1      Poor  TRUE
#> 2       2      Good FALSE
#> 2.1     2      Good FALSE
#> 1       3 Excellent FALSE
#> 3.1     1      Poor  TRUE

Si está haciendo coincidir varias columnas, primero deberá colapsarlas en una sola columna (con, por ejemplo, interaction ()). Sin embargo, normalmente es mejor cambiar a una función diseñada específicamente para unir varias tablas como merge() o dplyr::left_join().

4.5.3 Muestras aleatorias y bootstraps (subconjunto de enteros)

Puede usar índices enteros para muestrear o arrancar aleatoriamente un vector o un data frame. Simplemente use sample(n) para generar una permutación aleatoria de 1:n, y luego use los resultados para dividir los valores:

df <- data.frame(x = c(1, 2, 3, 1, 2), y = 5:1, z = letters[1:5])

# Reordenar aleatoriamente
df[sample(nrow(df)), ]
#>   x y z
#> 5 2 1 e
#> 3 3 3 c
#> 4 1 2 d
#> 1 1 5 a
#> 2 2 4 b

# Seleccionar aleatoriamente 3 filas
df[sample(nrow(df), 3), ]
#>   x y z
#> 4 1 2 d
#> 2 2 4 b
#> 1 1 5 a

# Seleccione 6 réplicas de arranque
df[sample(nrow(df), 6, replace = TRUE), ]
#>     x y z
#> 5   2 1 e
#> 5.1 2 1 e
#> 5.2 2 1 e
#> 2   2 4 b
#> 3   3 3 c
#> 3.1 3 3 c

Los argumentos de sample() controlan el número de muestras a extraer, y también si el muestreo se realiza con o sin reemplazo.

4.5.4 Ordenación (subconjunto de enteros)

order() toma un vector como entrada y devuelve un vector entero que describe cómo ordenar el vector dividido en subconjuntos²:

x <- c("b", "c", "a")
order(x)
#> [1] 3 1 2
x[order(x)]
#> [1] "a" "b" "c"

Para desempatar, puede proporcionar variables adicionales a order(). También puede cambiar el orden de ascendente a descendente utilizando decreasing = TRUE. De forma predeterminada, cualquier valor que falte se colocará al final del vector; sin embargo, puede eliminarlos con na.last = NA o ponerlos al frente con na.last = FALSE.

Para dos o más dimensiones, order() y el subconjunto de enteros facilita el orden de las filas o las columnas de un objeto:

# Reordenar al azar df
df2 <- df[sample(nrow(df)), 3:1]
df2
#>   z y x
#> 5 e 1 2
#> 1 a 5 1
#> 4 d 2 1
#> 2 b 4 2
#> 3 c 3 3

df2[order(df2$x), ]
#>   z y x
#> 1 a 5 1
#> 4 d 2 1
#> 5 e 1 2
#> 2 b 4 2
#> 3 c 3 3
df2[, order(names(df2))]
#>   x y z
#> 5 2 1 e
#> 1 1 5 a
#> 4 1 2 d
#> 2 2 4 b
#> 3 3 3 c

Puede ordenar los vectores directamente con sort(), o de manera similar dplyr::arrange(), para ordenar un data frame.

4.5.5 Expansión de recuentos agregados (subconjunto de enteros)

A veces obtiene un data frame donde filas idénticas se han colapsado en una y se ha agregado una columna de conteo. rep() y el subconjunto de enteros hacen que sea fácil de descomprimir, porque podemos aprovechar la vectorización de rep(): rep(x, y) repite x[i] y[i] veces .

df <- data.frame(x = c(2, 4, 1), y = c(9, 11, 6), n = c(3, 5, 1))
rep(1:nrow(df), df$n)
#> [1] 1 1 1 2 2 2 2 2 3

df[rep(1:nrow(df), df$n), ]
#>     x  y n
#> 1   2  9 3
#> 1.1 2  9 3
#> 1.2 2  9 3
#> 2   4 11 5
#> 2.1 4 11 5
#> 2.2 4 11 5
#> 2.3 4 11 5
#> 2.4 4 11 5
#> 3   1  6 1

4.5.6 Eliminar columnas de data frames (caracteres )

Hay dos formas de eliminar columnas de un data frame. Puede establecer columnas individuales para NULL:

df <- data.frame(x = 1:3, y = 3:1, z = letters[1:3])
df$z <- NULL

O puede extraer un subconjunto para devolver solo las columnas que desea:

df <- data.frame(x = 1:3, y = 3:1, z = letters[1:3])
df[c("x", "y")]
#>   x y
#> 1 1 3
#> 2 2 2
#> 3 3 1

Si solo conoce las columnas que no desea, use las operaciones de configuración para determinar qué columnas conservar:

df[setdiff(names(df), "z")]
#>   x y
#> 1 1 3
#> 2 2 2
#> 3 3 1

4.5.7 Selección de filas en función de una condición (subconjunto lógico)

Debido a que el subconjunto lógico le permite combinar fácilmente condiciones de varias columnas, es probablemente la técnica más utilizada para extraer filas de un data frame.

mtcars[mtcars$gear == 5, ]
#>                 mpg cyl  disp  hp drat   wt qsec vs am gear carb
#> Porsche 914-2  26.0   4 120.3  91 4.43 2.14 16.7  0  1    5    2
#> Lotus Europa   30.4   4  95.1 113 3.77 1.51 16.9  1  1    5    2
#> Ford Pantera L 15.8   8 351.0 264 4.22 3.17 14.5  0  1    5    4
#> Ferrari Dino   19.7   6 145.0 175 3.62 2.77 15.5  0  1    5    6
#> Maserati Bora  15.0   8 301.0 335 3.54 3.57 14.6  0  1    5    8

mtcars[mtcars$gear == 5 & mtcars$cyl == 4, ]
#>                mpg cyl  disp  hp drat   wt qsec vs am gear carb
#> Porsche 914-2 26.0   4 120.3  91 4.43 2.14 16.7  0  1    5    2
#> Lotus Europa  30.4   4  95.1 113 3.77 1.51 16.9  1  1    5    2

Recuerde utilizar los operadores booleanos vectoriales & y |, no los operadores escalares de cortocircuito && y ||, que son más útiles dentro de las sentencias if. Y no olvide las leyes de De Morgan, que pueden ser útiles para simplificar las negaciones:

• !(X & Y) es lo mismo que !X | !Y
• !(X | Y) es lo mismo que !X & !Y

Por ejemplo, !(X & !(Y | Z)) se simplifica en !X | !!(Y|Z), y luego a !X | Y | Z.

4.5.8 Álgebra booleana versus conjuntos (lógicos y enteros )

Es útil ser consciente de la equivalencia natural entre las operaciones con conjuntos (subconjuntos enteros) y el álgebra booleana (subconjuntos lógicos). El uso de operaciones de conjuntos es más efectivo cuando:

• Quieres encontrar el primero (o el último) TRUE.

• Tienes muy pocos TRUE y muchos FALSE; una representación establecida puede ser más rápida y requerir menos almacenamiento.

which() le permite convertir una representación booleana en una representación entera. No hay una operación inversa en la base R, pero podemos crear una fácilmente:

x <- sample(10) < 4
which(x)
#> [1] 2 3 4

unwhich <- function(x, n) {
  out <- rep_len(FALSE, n)
  out[x] <- TRUE
  out
}
unwhich(which(x), 10)
#>  [1] FALSE  TRUE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE

Creemos dos vectores lógicos y sus equivalentes enteros, y luego exploremos la relación entre las operaciones booleanas y de conjuntos.

(x1 <- 1:10 %% 2 == 0)
#>  [1] FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE  TRUE
(x2 <- which(x1))
#> [1]  2  4  6  8 10
(y1 <- 1:10 %% 5 == 0)
#>  [1] FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE
(y2 <- which(y1))
#> [1]  5 10

# X & Y <-> intersect(x, y)
x1 & y1
#>  [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE
intersect(x2, y2)
#> [1] 10

# X | Y <-> union(x, y)
x1 | y1
#>  [1] FALSE  TRUE FALSE  TRUE  TRUE  TRUE FALSE  TRUE FALSE  TRUE
union(x2, y2)
#> [1]  2  4  6  8 10  5

# X & !Y <-> setdiff(x, y)
x1 & !y1
#>  [1] FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE FALSE
setdiff(x2, y2)
#> [1] 2 4 6 8

# xor(X, Y) <-> setdiff(union(x, y), intersect(x, y))
xor(x1, y1)
#>  [1] FALSE  TRUE FALSE  TRUE  TRUE  TRUE FALSE  TRUE FALSE FALSE
setdiff(union(x2, y2), intersect(x2, y2))
#> [1] 2 4 6 8 5

Al aprender subconjuntos por primera vez, un error común es usar x[which(y)] en lugar de x[y]. Aquí, which() no logra nada: cambia de subconjunto lógico a entero, pero el resultado es exactamente el mismo. En casos más generales, hay dos diferencias importantes.

• Cuando el vector lógico contiene NA, el subconjunto lógico reemplaza estos valores con NA mientras que which() simplemente elimina estos valores. No es raro usar which() para este efecto secundario, pero no lo recomiendo: nada sobre el nombre “cuál” implica la eliminación de valores faltantes.

• x[-which(y)] no es equivalente a x[!y]: si y es todo FALSO, which(y) será integer(0) y -integer(0) sigue siendo integer(0), por lo que no obtendrá valores, en lugar de todos los valores.

En general, evite cambiar de subconjunto lógico a entero a menos que desee, por ejemplo, el primer o último valor TRUE.

4.5.9 Ejercicios

1. ¿Cómo permutarías aleatoriamente las columnas de un data frame? (Esta es una técnica importante en los bosques aleatorios). ¿Puede permutar simultáneamente las filas y las columnas en un solo paso?

2. ¿Cómo seleccionaría una muestra aleatoria de m filas de un data frame? ¿Qué pasaría si la muestra tuviera que ser contigua (es decir, con una fila inicial, una fila final y todas las filas intermedias)?

3. ¿Cómo podría poner las columnas en un data frame en orden alfabético?

4.6 Respuestas de la

1. Los enteros positivos seleccionan elementos en posiciones específicas, los enteros negativos descartan elementos; los vectores lógicos mantienen los elementos en las posiciones correspondientes a TRUE; los vectores de caracteres seleccionan elementos con nombres coincidentes.

2. [ selecciona sub-listas: siempre devuelve una lista. Si lo usa con un solo entero positivo, devuelve una lista de longitud uno. [[ selecciona un elemento dentro de una lista. $ es una abreviatura conveniente: x$y es equivalente a x[["y"]].

3. Use drop = FALSE si está creando subconjuntos de una matriz, un arreglo o un data frame y desea conservar las dimensiones originales. Casi siempre deberías usarlo cuando hagas subconjuntos dentro de una función.

4. Si x es una matriz, x[] <- 0 reemplazará cada elemento con 0, manteniendo el mismo número de filas y columnas. Por el contrario, x <- 0 reemplaza completamente la matriz con el valor 0.

5. Un vector de caracteres con nombre puede actuar como una tabla de búsqueda simple: c(x = 1, y = 2, z = 3)[c("y", "z", "x")]

---

1. Si viene de Python, es probable que esto sea confuso, ya que probablemente esperaría que df[1:3, 1:2] seleccione tres columnas y dos filas. Generalmente, R “piensa” en las dimensiones en términos de filas y columnas, mientras que Python lo hace en términos de columnas y filas.

2. Estos son índices de “extracción”, es decir, order(x)[i] es un índice de dónde se encuentra cada x[i]. No es un índice de dónde debe enviarse x[i].