9 Funcionales

9.1 Introducción

Para volverse significativamente más confiable, el código debe volverse más transparente. En particular, las condiciones anidadas y los bucles deben verse con gran sospecha. Los flujos de control complicados confunden a los programadores. El código desordenado a menudo esconde errores.

— Bjarne Stroustrup

Un funcional es una función que toma una función como entrada y devuelve un vector como salida. Aquí hay un funcional simple: llama a la función proporcionada como entrada con 1000 números uniformes aleatorios.

randomise <- function(f) f(runif(1e3))
randomise(mean)
#> [1] 0.506
randomise(mean)
#> [1] 0.501
randomise(sum)
#> [1] 489

Lo más probable es que ya hayas usado un funcional. Es posible que haya utilizado reemplazos de bucle for como lapply(), apply() y tapply() de base R; o map() de purrr; o quizás hayas usado un funcional matemático como integrate() u optim().

Un uso común de los funcionales es como una alternativa a los bucles for. Los bucles for tienen mala reputación en R porque mucha gente cree que son lentos[^funcionals-1], pero la verdadera desventaja de los bucles for es que son muy flexibles: un bucle transmite que estás iterando, pero no lo que deberías terminar con los resultados. Así como es mejor usar while que repeat, y es mejor usar for que while (Sección 5.3.2), es mejor usar un funcional que for. Cada funcional está diseñado para una tarea específica, por lo que cuando reconoce el funcional, inmediatamente sabe por qué se está utilizando.

Si es un usuario experimentado de bucles for, cambiar a funcionales suele ser un ejercicio de coincidencia de patrones. Miras el bucle for y encuentras un funcional que coincida con la forma básica. Si no existe uno, no intente torturar un funcional existente para que se ajuste a la forma que necesita. ¡En su lugar, déjalo como un bucle for! (O una vez que haya repetido el mismo bucle dos o más veces, tal vez piense en escribir su propio funcional).

Outline

La Sección 9.2 introduce tu primer funcional: purrr :: map ().
La Sección 9.3 demuestra cómo puede combinar múltiples funciones simples para resolver un problema más complejo y analiza cómo el estilo purrr difiere de otros enfoques.
La Sección 9.4 te enseña alrededor de 18 (!!) variantes importantes de purrr::map(). Afortunadamente, su diseño ortogonal los hace fáciles de aprender, recordar y dominar.
La Sección 9.5 introduce un nuevo estilo de funcional: purrr::reduce(). reduce() reduce sistemáticamente un vector a un solo resultado mediante la aplicación de una función que toma dos entradas.
La Sección 9.6 te enseña acerca de los predicados: funciones que devuelven un solo TRUE o FALSE, y la familia de funciones que los usan para resolver problemas comunes.
La Sección 9.7 revisa algunos funcionales en base R que no son miembros de las familias map, reduce o predicate.

Requsisitos previos

Este capítulo se centrará en las funciones proporcionadas por el paquete purrr (Henry y Wickham 2018). Estas funciones tienen una interfaz consistente que facilita la comprensión de las ideas clave que sus equivalentes básicos, que han crecido orgánicamente durante muchos años. Compararé y contrastaré las funciones básicas de R a medida que avanzamos, y luego terminaré el capítulo con una discusión de las funciones básicas que no tienen equivalentes purrr.

library(purrr)

9.2 My first functional: `map()`

El funcional más fundamental es purrr::map()[^funcionals-2]. Toma un vector y una función, llama a la función una vez por cada elemento del vector y devuelve los resultados en una lista. En otras palabras, map(1:3, f) es equivalente a list(f(1), f(2), f(3)).

triple <- function(x) x * 3
map(1:3, triple)
#> [[1]]
#> [1] 3
#> 
#> [[2]]
#> [1] 6
#> 
#> [[3]]
#> [1] 9

O, gráficamente:

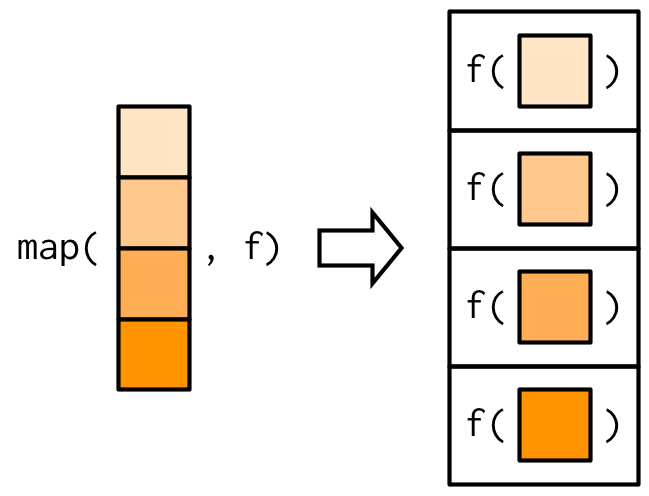
Quizás se pregunte por qué esta función se llama map(). ¿Qué tiene que ver con representar las características físicas de la tierra o el mar 🗺? De hecho, el significado proviene de las matemáticas donde mapa se refiere a “una operación que asocia cada elemento de un conjunto dado con uno o más elementos de un segundo conjunto”. Esto tiene sentido aquí porque map() define un mapeo de un vector a otro. (“Map” también tiene la agradable propiedad de ser corto, lo cual es útil para un bloque de construcción tan fundamental).

La implementación de map() es bastante simple. Asignamos una lista de la misma longitud que la entrada y luego completamos la lista con un bucle for. El corazón de la implementación es solo un puñado de líneas de código:

simple_map <- function(x, f, ...) {
  out <- vector("list", length(x))
  for (i in seq_along(x)) {
    out[[i]] <- f(x[[i]], ...)
  }
  out
}

La verdadera función purrr::map() tiene algunas diferencias: está escrita en C para aprovechar hasta el último ápice de rendimiento, conserva los nombres y admite algunos atajos que aprenderá en la Sección 9.2.2.

El equivalente básico de map() es lapply(). La única diferencia es que lapply() no es compatible con los asistentes que aprenderá a continuación, por lo que si solo está usando map() de purrr, puede omitir la dependencia adicional y usar lapply() directamente.

9.2.1 Producción de vectores atómicos

map() devuelve una lista, lo que la convierte en la más general de la familia de mapas porque puedes poner cualquier cosa en una lista. Pero es un inconveniente devolver una lista cuando lo haría una estructura de datos más simple, por lo que hay cuatro variantes más específicas: map_lgl(), map_int(), map_dbl() y map_chr(). Cada uno devuelve un vector atómico del tipo especificado:

# map_chr() siempre devuelve un vector de caracteres
map_chr(mtcars, typeof)
#>      mpg      cyl     disp       hp     drat       wt     qsec       vs 
#> "double" "double" "double" "double" "double" "double" "double" "double" 
#>       am     gear     carb 
#> "double" "double" "double"

# map_lgl() siempre devuelve un vector de valore boleanos
map_lgl(mtcars, is.double)
#>  mpg  cyl disp   hp drat   wt qsec   vs   am gear carb 
#> TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE

# map_int() siempre devuelve un vector de números enteros
n_unique <- function(x) length(unique(x))
map_int(mtcars, n_unique)
#>  mpg  cyl disp   hp drat   wt qsec   vs   am gear carb 
#>   25    3   27   22   22   29   30    2    2    3    6

# map_dbl() siempre devuelve un vector doble
map_dbl(mtcars, mean)
#>     mpg     cyl    disp      hp    drat      wt    qsec      vs      am    gear 
#>  20.091   6.188 230.722 146.688   3.597   3.217  17.849   0.438   0.406   3.688 
#>    carb 
#>   2.812

purrr usa la convención de que los sufijos, como _dbl(), se refieren a la salida. Todas las funciones map_*() pueden tomar cualquier tipo de vector como entrada. Estos ejemplos se basan en dos hechos: mtcars es un data frame y los data frames son listas que contienen vectores de la misma longitud. Esto es más obvio si dibujamos un data frame con la misma orientación que el vector:

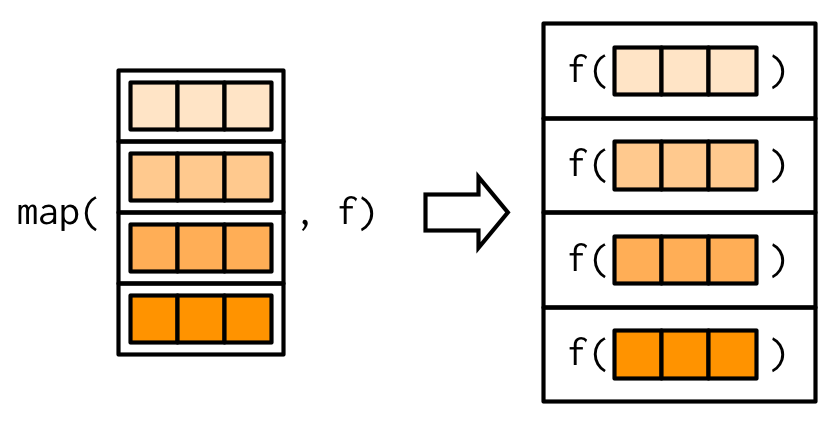
Todas las funciones de mapa siempre devuelven un vector de salida de la misma longitud que la entrada, lo que implica que cada llamada a .f debe devolver un solo valor. Si no es así, obtendrá un error:

pair <- function(x) c(x, x)
map_dbl(1:2, pair)
#> Error in `map_dbl()`:
#> ℹ In index: 1.
#> Caused by error:
#> ! Result must be length 1, not 2.

Esto es similar al error que obtendrá si .f devuelve el tipo de resultado incorrecto:

map_dbl(1:2, as.character)
#> Error in `map_dbl()`:
#> ℹ In index: 1.
#> Caused by error:
#> ! Can't coerce from a string to a double.

En cualquier caso, a menudo es útil volver a map(), porque map() puede aceptar cualquier tipo de salida. Eso le permite ver la salida problemática y averiguar qué hacer con ella.

map(1:2, pair)
#> [[1]]
#> [1] 1 1
#> 
#> [[2]]
#> [1] 2 2
map(1:2, as.character)
#> [[1]]
#> [1] "1"
#> 
#> [[2]]
#> [1] "2"

Base R tiene dos funciones de aplicación que pueden devolver vectores atómicos: sapply() y vapply(). Te recomiendo que evites sapply() porque intenta simplificar el resultado, por lo que puede devolver una lista, un vector o una matriz. Esto dificulta la programación y debe evitarse en entornos no interactivos. vapply() es más seguro porque le permite proporcionar una plantilla, FUN.VALUE, que describe la forma de salida. Si no quieres usar purrr, te recomiendo que siempre uses vapply() en tus funciones, no sapply(). La principal desventaja de vapply() es su verbosidad: por ejemplo, el equivalente a map_dbl(x, mean, na.rm = TRUE) es vapply(x, mean, na.rm = TRUE, FUN.VALUE = doble(1)).

9.2.2 Funciones y accesos directos anónimos

En lugar de usar map() con una función existente, puede crear una función anónima en línea (como se menciona en la Sección 6.2.3):

map_dbl(mtcars, function(x) length(unique(x)))
#>  mpg  cyl disp   hp drat   wt qsec   vs   am gear carb 
#>   25    3   27   22   22   29   30    2    2    3    6

Las funciones anónimas son muy útiles, pero la sintaxis es detallada. Así que purrr admite un atajo especial:

map_dbl(mtcars, ~ length(unique(.x)))
#>  mpg  cyl disp   hp drat   wt qsec   vs   am gear carb 
#>   25    3   27   22   22   29   30    2    2    3    6

Esto funciona porque todas las funciones purrr traducen fórmulas, creadas por ~ (pronunciado “twiddle”), en funciones. Puedes ver lo que sucede detrás de escena llamando a as_mapper():

as_mapper(~ length(unique(.x)))
#> <lambda>
#> function (..., .x = ..1, .y = ..2, . = ..1) 
#> length(unique(.x))
#> attr(,"class")
#> [1] "rlang_lambda_function" "function"

Los argumentos de la función parecen un poco extravagantes pero le permiten referirse a . para funciones de un argumento, .x y .y para funciones de dos argumentos, y ..1, ..2, . .3, etc., para funciones con un número arbitrario de argumentos. . permanece para la compatibilidad con versiones anteriores, pero no recomiendo usarlo porque se confunde fácilmente con el . utilizado por la canalización de magrittr.

Este atajo es particularmente útil para generar datos aleatorios:

x <- map(1:3, ~ runif(2))
str(x)
#> List of 3
#>  $ : num [1:2] 0.281 0.53
#>  $ : num [1:2] 0.433 0.917
#>  $ : num [1:2] 0.0275 0.8249

Reserve esta sintaxis para funciones cortas y simples. Una buena regla general es que si su función abarca líneas o usa {}, es hora de darle un nombre.

Las funciones del mapa también tienen atajos para extraer elementos de un vector, impulsados por purrr::pluck(). Puede utilizar un vector de caracteres para seleccionar elementos por nombre, un vector entero para seleccionar por posición o una lista para seleccionar tanto por nombre como por posición. Estos son muy útiles para trabajar con listas profundamente anidadas, que a menudo surgen cuando se trabaja con JSON.

x <- list(
  list(-1, x = 1, y = c(2), z = "a"),
  list(-2, x = 4, y = c(5, 6), z = "b"),
  list(-3, x = 8, y = c(9, 10, 11))
)

# Selecciona por nombre
map_dbl(x, "x")
#> [1] 1 4 8

# O por posición
map_dbl(x, 1)
#> [1] -1 -2 -3

# Or por ambos
map_dbl(x, list("y", 1))
#> [1] 2 5 9

# Obtendrá un error si un componente no existe:
map_chr(x, "z")
#> Error in `map_chr()`:
#> ℹ In index: 3.
#> Caused by error:
#> ! Result must be length 1, not 0.

# A menos que proporcione un valor .default
map_chr(x, "z", .default = NA)
#> [1] "a" "b" NA

En las funciones básicas de R, como lapply(), puede proporcionar el nombre de la función como una cadena. Esto no es tremendamente útil ya que lapply(x, "f") es casi siempre equivalente a lapply(x, f) y es más tipeo.

9.2.3 Pasar argumentos con `...`

A menudo es conveniente pasar argumentos adicionales a la función que está llamando. Por ejemplo, es posible que desee pasar na.rm = TRUE junto con mean(). Una forma de hacerlo es con una función anónima:

x <- list(1:5, c(1:10, NA))
map_dbl(x, ~ mean(.x, na.rm = TRUE))
#> [1] 3.0 5.5

Pero debido a que las funciones del mapa pasan ..., hay una forma más simple disponible:

map_dbl(x, mean, na.rm = TRUE)
#> [1] 3.0 5.5

Esto es más fácil de entender con una imagen: cualquier argumento que viene después de f en la llamada a map() se inserta después de los datos en llamadas individuales a f():

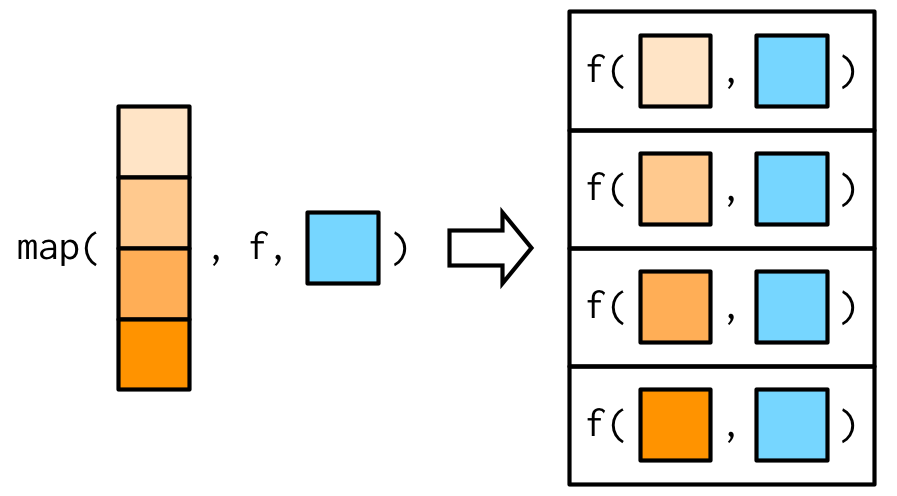
Es importante tener en cuenta que estos argumentos no están descompuestos; o dicho de otra manera, map() solo se vectoriza sobre su primer argumento. Si un argumento después de f es un vector, se pasará como está:

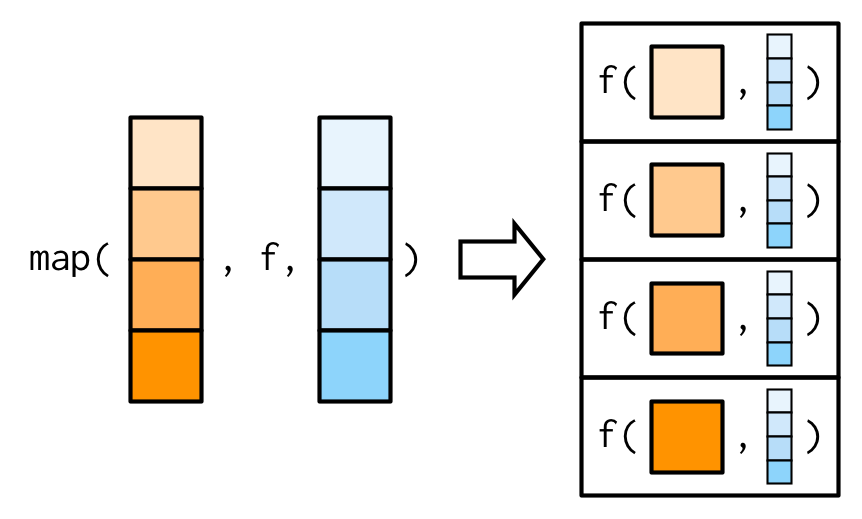
(Aprenderá acerca de las variantes de mapa que están vectorizadas sobre múltiples argumentos en las Secciones Sección 9.4.2 y Sección 9.4.5.)

Tenga en cuenta que hay una sutil diferencia entre colocar argumentos adicionales dentro de una función anónima en comparación con pasarlos a map(). Ponerlos en una función anónima significa que serán evaluados cada vez que se ejecute f(), no solo una vez cuando llames a map(). Esto es más fácil de ver si hacemos que el argumento adicional sea aleatorio:

plus <- function(x, y) x + y

x <- c(0, 0, 0, 0)
map_dbl(x, plus, runif(1))
#> [1] 0.0625 0.0625 0.0625 0.0625
map_dbl(x, ~ plus(.x, runif(1)))
#> [1] 0.903 0.132 0.629 0.945

9.2.4 Nombres de argumentos

En los diagramas, he omitido los nombres de los argumentos para centrarme en la estructura general. Pero recomiendo escribir los nombres completos en su código, ya que lo hace más fácil de leer. map(x, mean, 0.1) es un código perfectamente válido, pero llamará mean(x[[1]], 0.1) por lo que depende de que el lector recuerde que el segundo argumento de mean() es trim. Para evitar una carga innecesaria en el cerebro del lector[^funcionals-3], sea amable y escriba map(x, mean, trim = 0.1).

Esta es la razón por la que los argumentos de map() son un poco extraños: en lugar de ser x y f, son .x y .f. Es más fácil ver el problema que conduce a estos nombres usando simple_map() definido anteriormente. simple_map() tiene argumentos x y f, por lo que tendrá problemas cada vez que la función a la que llama tenga argumentos x o f:

bootstrap_summary <- function(x, f) {
  f(sample(x, replace = TRUE))
}

simple_map(mtcars, bootstrap_summary, f = mean)
#> Error in mean.default(x[[i]], ...): 'trim' must be numeric of length one

El error es un poco desconcertante hasta que recuerdas que la llamada a simple_map() es equivalente a simple_map(x = mtcars, f = mean, bootstrap_summary) porque la coincidencia con nombre supera a la coincidencia posicional.

Las funciones purrr reducen la probabilidad de que se produzca un conflicto de este tipo mediante el uso de .f y .x en lugar de las más comunes f y x. Por supuesto, esta técnica no es perfecta (porque la función a la que está llamando aún puede usar .f y .x), pero evita el 99% de los problemas. El 1% restante del tiempo, utilice una función anónima.

Las funciones base que transmiten ... usan una variedad de convenciones de nomenclatura para evitar la coincidencia de argumentos no deseados:

La familia apply utiliza principalmente letras mayúsculas (por ejemplo, X y FUN).
transform() usa el prefijo más exótico _: esto hace que el nombre no sea sintáctico, por lo que siempre debe estar entre `, como se describe en la Sección 2.2.1. Esto hace que las coincidencias no deseadas sean extremadamente improbables.
Otras funciones como uniroot() y optim() no hacen ningún esfuerzo por evitar conflictos, pero tienden a usarse con funciones especialmente creadas, por lo que es menos probable que se produzcan conflictos.

9.2.5 Variando otro argumento

Hasta ahora, el primer argumento de map() siempre se ha convertido en el primer argumento de la función. Pero, ¿qué sucede si el primer argumento debe ser constante y desea variar un argumento diferente? ¿Cómo se obtiene el resultado en esta imagen?

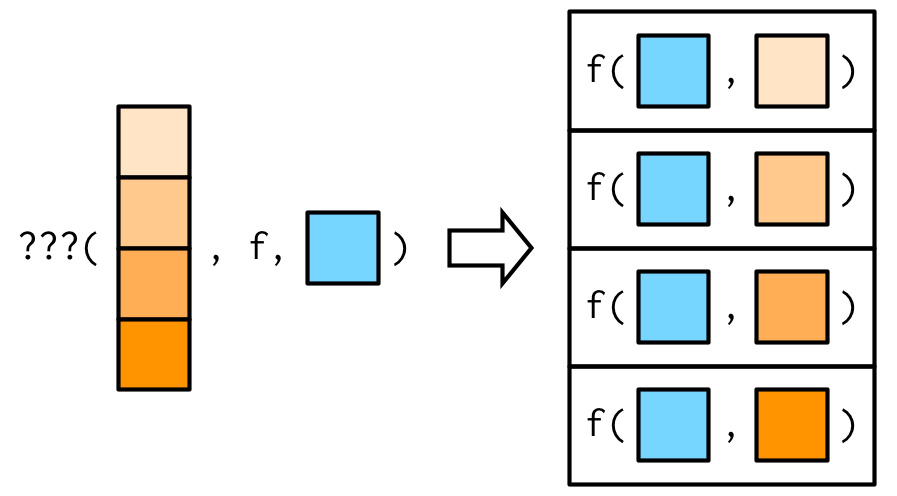
Resulta que no hay forma de hacerlo directamente, pero hay dos trucos que puedes usar en su lugar. Para ilustrarlos, imagine que tengo un vector que contiene algunos valores inusuales y quiero explorar el efecto de diferentes cantidades de recorte al calcular la media. En este caso, el primer argumento de mean() será constante, y quiero variar el segundo argumento, trim.

trims <- c(0, 0.1, 0.2, 0.5)
x <- rcauchy(1000)

La técnica más simple es usar una función anónima para reorganizar el orden de los argumentos:
```
map_dbl(trims, ~ mean(x, trim = .x))
#> [1] -0.3500  0.0434  0.0354  0.0502
```
Esto todavía es un poco confuso porque estoy usando x y .x. Puedes hacerlo un poco más claro abandonando el ayudante ~:
```
map_dbl(trims, function(trim) mean(x, trim = trim))
#> [1] -0.3500  0.0434  0.0354  0.0502
```
A veces, si quiere ser (demasiado) inteligente, puede aprovechar las reglas flexibles de coincidencia de argumentos de R (como se describe en la Sección 6.8.2). Por ejemplo, en este ejemplo puede reescribir mean(x, trim = 0.1) como mean(0.1, x = x), por lo que podría escribir la llamada a map_dbl() como:
```
map_dbl(trims, mean, x = x)
#> [1] -0.3500  0.0434  0.0354  0.0502
```
No recomiendo esta técnica ya que se basa en la familiaridad del lector con el orden de los argumentos en .f y las reglas de coincidencia de argumentos de R.

Verá una alternativa más en la Sección 9.4.5.

9.2.6 Ejercicios

Utilice as_mapper() para explorar cómo purrr genera funciones anónimas para los ayudantes de enteros, caracteres y listas. ¿Qué ayudante te permite extraer atributos? Lea la documentación para averiguarlo.
map(1:3, ~ runif(2)) es un patrón útil para generar números aleatorios, pero map(1:3, runif(2)) no lo es. ¿Por qué no? ¿Puede explicar por qué devuelve el resultado que lo hace?
Use la función map() apropiada para:
1. Calcule la desviación estándar de cada columna en un data frame numéricos.
2. Calcule la desviación estándar de cada columna numérica en un data frame mixto. (Sugerencia: deberá hacerlo en dos pasos).
3. Calcule el número de niveles para cada factor en un data frame.
El siguiente código simula el rendimiento de una prueba t para datos no normales. Extraiga el valor p de cada prueba, luego visualice.
```
trials <- map(1:100, ~ t.test(rpois(10, 10), rpois(7, 10)))
```

El siguiente código usa un mapa anidado dentro de otro mapa para aplicar una función a cada elemento de una lista anidada. ¿Por qué falla y qué debe hacer para que funcione?

x <- list(
  list(1, c(3, 9)),
  list(c(3, 6), 7, c(4, 7, 6))
)

triple <- function(x) x * 3
map(x, map, .f = triple)
#> Error in `map()`:
#> ℹ In index: 1.
#> Caused by error in `.f()`:
#> ! unused argument (function (.x, .f, ..., .progress = FALSE) 
#> {
#>     map_("list", .x, .f, ..., .progress = .progress)
#> })

Use map() para ajustar modelos lineales al conjunto de datos mtcars usando las fórmulas almacenadas en esta lista:

formulas <- list(
  mpg ~ disp,
  mpg ~ I(1 / disp),
  mpg ~ disp + wt,
  mpg ~ I(1 / disp) + wt
)

Ajuste el modelo mpg ~ disp a cada una de las réplicas de arranque de mtcars en la lista a continuación, luego extraiga el \(R^2\) del ajuste del modelo (Sugerencia: puede calcular el \(R^2\) con summary ().)
```
bootstrap <- function(df) {
  df[sample(nrow(df), replace = TRUE), , drop = FALSE]
}

bootstraps <- map(1:10, ~ bootstrap(mtcars))
```

9.3 Estilo Purrr

Antes de continuar explorando más variantes de mapas, echemos un vistazo rápido a cómo tiende a usar varias funciones purrr para resolver un problema moderadamente realista: ajustar un modelo a cada subgrupo y extraer un coeficiente del modelo. Para este ejemplo de juguete, voy a dividir el conjunto de datos mtcars en grupos definidos por el número de cilindros, utilizando la función base split:

by_cyl <- split(mtcars, mtcars$cyl)

Esto crea una lista de tres data frames: los automóviles con 4, 6 y 8 cilindros respectivamente.

Ahora imagine que queremos ajustar un modelo lineal, luego extraiga el segundo coeficiente (es decir, la pendiente). El siguiente código muestra cómo puede hacer eso con purrr:

by_cyl |> 
  map(~ lm(mpg ~ wt, data = .x)) |> 
  map(coef) |> 
  map_dbl(2)
#>     4     6     8 
#> -5.65 -2.78 -2.19

(Si no ha visto |>, la canalización, antes, se describe en la Sección 6.3.)

Creo que este código es fácil de leer porque cada línea encapsula un solo paso, puedes distinguir fácilmente lo funcional de lo que hace, y los ayudantes purrr nos permiten describir de manera muy concisa qué hacer en cada paso.

¿Cómo atacarías este problema con la base R? Ciertamente podría reemplazar cada función purrr con la función base equivalente:

by_cyl |>  
  lapply(function(data) lm(mpg ~ wt, data = data)) |> 
  lapply(coef) |> 
  vapply(function(x) x[[2]], double(1))
#>     4     6     8 
#> -5.65 -2.78 -2.19

O, por supuesto, podría usar un bucle for:

slopes <- double(length(by_cyl))
for (i in seq_along(by_cyl)) {
  model <- lm(mpg ~ wt, data = by_cyl[[i]])
  slopes[[i]] <- coef(model)[[2]]
}
slopes
#> [1] -5.65 -2.78 -2.19

Es interesante notar que a medida que pasa de purrr a aplicar funciones básicas a bucles for, tiende a hacer más y más en cada iteración. En purrr iteramos 3 veces (map(), map(), map_dbl()), con funciones apply iteramos dos veces (lapply(), vapply()), y con un for loop iteramos una vez. Prefiero más pasos, pero más simples, porque creo que hace que el código sea más fácil de entender y luego modificar.

9.4 Variantes de map

Hay 23 variantes principales de map(). Hasta ahora, ha aprendido acerca de cinco (map(), map_lgl(), map_int(), map_dbl() y map_chr()). Eso significa que tienes 18 (!!) más para aprender. Eso parece mucho, pero afortunadamente el diseño de purrr significa que solo necesitas aprender cinco nuevas ideas:

Salida del mismo tipo que la entrada con modify()
Iterar sobre dos entradas con map2().
Iterar con un índice usando imap()
No devuelve nada con walk().
Iterar sobre cualquier número de entradas con pmap().

La familia de funciones del mapa tiene entradas y salidas ortogonales, lo que significa que podemos organizar toda la familia en una matriz, con entradas en las filas y salidas en las columnas. Una vez que haya dominado la idea en una fila, puede combinarla con cualquier columna; una vez que haya dominado la idea en una columna, puede combinarla con cualquier fila. Esa relación se resume en el siguiente cuadro:

	List	Atómico	El mismo tipo	Nada
Un argumento	`map()`	`map_lgl()`, …	`modify()`	`walk()`
Dos argumentos	`map2()`	`map2_lgl()`, …	`modify2()`	`walk2()`
Un argumento + índice	`imap()`	`imap_lgl()`, …	`imodify()`	`iwalk()`
N argumentos	`pmap()`	`pmap_lgl()`, …	—	`pwalk()`

9.4.1 Mismo tipo de salida que de entrada: `modify()`

Imagina que quisieras duplicar cada columna en un data frame. Primero puede intentar usar map(), pero map() siempre devuelve una lista:

df <- data.frame(
  x = 1:3,
  y = 6:4
)

map(df, ~ .x * 2)
#> $x
#> [1] 2 4 6
#> 
#> $y
#> [1] 12 10  8

Si desea mantener la salida como un data frame, puede usar modify(), que siempre devuelve el mismo tipo de salida que la entrada:

modify(df, ~ .x * 2)
#>   x  y
#> 1 2 12
#> 2 4 10
#> 3 6  8

A pesar del nombre, modify() no modifica en su lugar, devuelve una copia modificada, por lo que si desea modificar permanentemente df, debe asignarlo:

df <- modify(df, ~ .x * 2)

Como de costumbre, la implementación básica de modify() es simple y, de hecho, es incluso más simple que map() porque no necesitamos crear un nuevo vector de salida; podemos simplemente reemplazar progresivamente la entrada. (El código real es un poco complejo para manejar casos extremos con más gracia).

simple_modify <- function(x, f, ...) {
  for (i in seq_along(x)) {
    x[[i]] <- f(x[[i]], ...)
  }
  x
}

En la Sección 9.6.2 aprenderá sobre una variante muy útil de modify(), llamada modify_if(). Esto le permite (p. ej.) solo duplicar columnas numéricas de un data frame con modify_if(df, is.numeric, ~ .x * 2).

9.4.2 Dos entradas: `map2()` y amigos

map() se vectoriza sobre un único argumento, .x. Esto significa que solo varía .x cuando se llama a .f, y todos los demás argumentos se pasan sin cambios, por lo que no es adecuado para algunos problemas. Por ejemplo, ¿cómo encontraría una media ponderada cuando tiene una lista de observaciones y una lista de pesos? Imagina que tenemos los siguientes datos:

xs <- map(1:8, ~ runif(10))
xs[[1]][[1]] <- NA
ws <- map(1:8, ~ rpois(10, 5) + 1)

Puedes usar map_dbl() para calcular las medias no ponderadas:

map_dbl(xs, mean)
#> [1]    NA 0.463 0.551 0.453 0.564 0.501 0.371 0.443

Pero pasar ws como argumento adicional no funciona porque los argumentos después de .f no se transforman:

map_dbl(xs, weighted.mean, w = ws)
#> Error in `map_dbl()`:
#> ℹ In index: 1.
#> Caused by error in `weighted.mean.default()`:
#> ! 'x' and 'w' must have the same length

Necesitamos una nueva herramienta: un map2(), que se vectoriza sobre dos argumentos. Esto significa que tanto .x como .y varían en cada llamada a .f:

map2_dbl(xs, ws, weighted.mean)
#> [1]    NA 0.451 0.603 0.452 0.563 0.510 0.342 0.464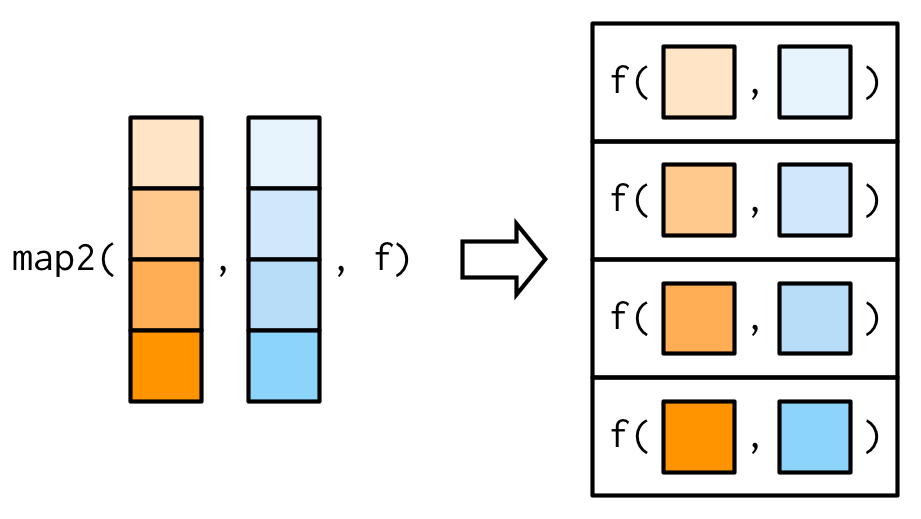

Los argumentos de map2() son ligeramente diferentes a los argumentos de map() ya que dos vectores vienen antes de la función, en lugar de uno. Los argumentos adicionales todavía van después:

map2_dbl(xs, ws, weighted.mean, na.rm = TRUE)
#> [1] 0.504 0.451 0.603 0.452 0.563 0.510 0.342 0.464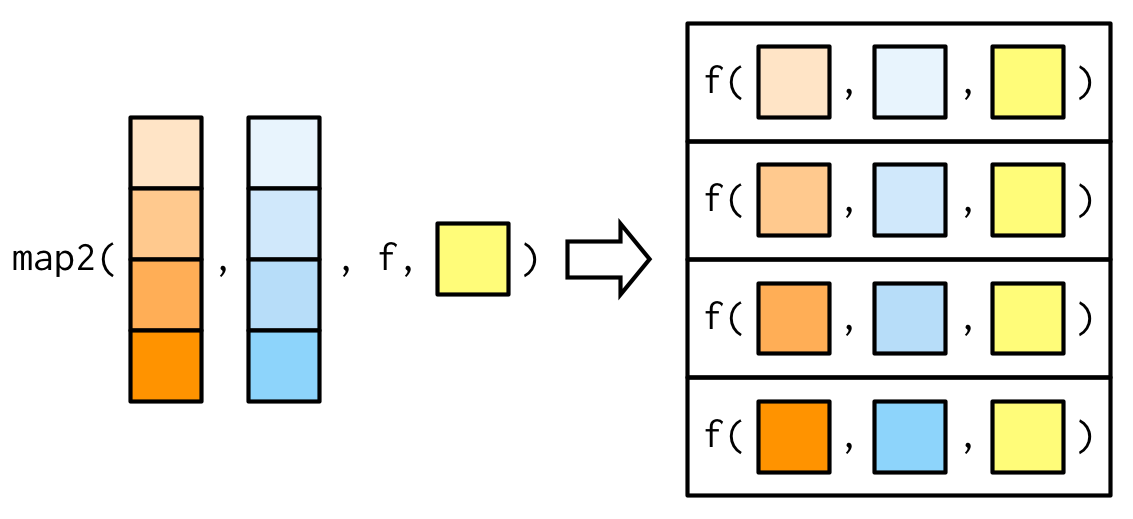

La implementación básica de map2() es simple y bastante similar a la de map(). En lugar de iterar sobre un vector, iteramos sobre dos en paralelo:

simple_map2 <- function(x, y, f, ...) {
  out <- vector("list", length(x))
  for (i in seq_along(x)) {
    out[[i]] <- f(x[[i]], y[[i]], ...)
  }
  out
}

Una de las grandes diferencias entre map2() y la función simple anterior es que map2() recicla sus entradas para asegurarse de que tengan la misma longitud:

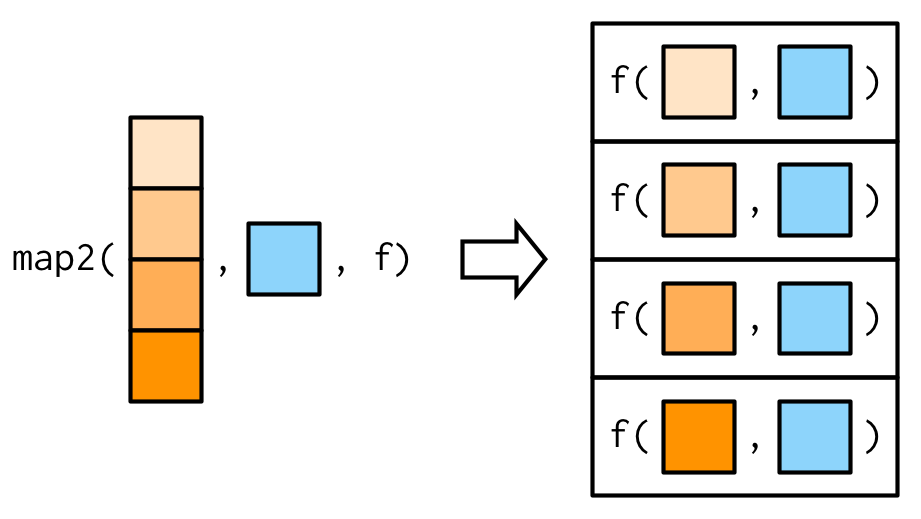
En otras palabras, map2(x, y, f) automáticamente se comportará como map(x, f, y) cuando sea necesario. Esto es útil al escribir funciones; en las secuencias de comandos, generalmente solo usaría la forma más simple directamente.

La base equivalente más cercana a map2() es Map(), que se analiza en la Sección 9.4.5.

9.4.3 Sin salidas: `walk()` y amigos

La mayoría de las funciones se llaman por el valor que devuelven, por lo que tiene sentido capturar y almacenar el valor con una función map(). Pero algunas funciones se llaman principalmente por sus efectos secundarios (por ejemplo, cat(), write.csv() o ggsave()) y no tiene sentido capturar sus resultados. Toma este ejemplo simple que muestra un mensaje de bienvenida usando cat(). cat() devuelve NULL, así que mientras map() funciona (en el sentido de que genera las bienvenidas deseadas), también devuelve list(NULL, NULL).

welcome <- function(x) {
  cat("Welcome ", x, "!\n", sep = "")
}
names <- c("Hadley", "Jenny")

# Además de generar las bienvenidas, también muestra
# el valor de retorno de cat()
map(names, welcome)
#> Welcome Hadley!
#> Welcome Jenny!
#> [[1]]
#> NULL
#> 
#> [[2]]
#> NULL

Podrías evitar este problema asignando los resultados de map() a una variable que nunca usas, pero que enturbiaría la intención del código. En su lugar, purrr proporciona la familia de funciones walk que ignoran los valores de retorno de .f y en su lugar devuelven .x de forma invisible¹.

walk(names, welcome)
#> Welcome Hadley!
#> Welcome Jenny!

Mi representación visual de caminar intenta capturar la importante diferencia con map(): las salidas son efímeras y la entrada se devuelve de forma invisible.

Una de las variantes de walk() más útiles es walk2() porque un efecto secundario muy común es guardar algo en el disco, y cuando guardas algo en el disco siempre tienes un par de valores: el objeto y la ruta que en el que desea guardarlo.

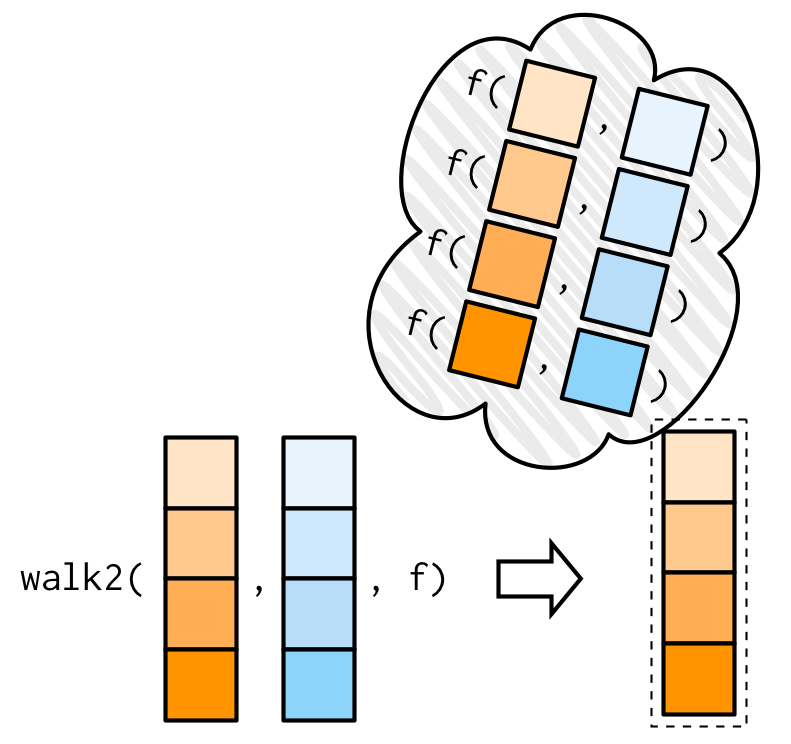
Por ejemplo, imagina que tienes una lista de data frames (que he creado aquí usando split()) y te gustaría guardar cada uno en un archivo CSV separado. Eso es fácil con walk2():

temp <- tempfile()
dir.create(temp)

cyls <- split(mtcars, mtcars$cyl)
paths <- file.path(temp, paste0("cyl-", names(cyls), ".csv"))
walk2(cyls, paths, write.csv)

dir(temp)
#> [1] "cyl-4.csv" "cyl-6.csv" "cyl-8.csv"

Aquí el walk2 () es equivalente a write.csv(cyls[[1]], paths[[1]]), write.csv(cyls[[2]], paths[[2]]), write.csv(cyls[[3]], paths[[3]]).

No existe una base equivalente a walk(); envuelva el resultado de lapply() en invisible() o guárdelo en una variable que nunca se use.

9.4.4 Iterando sobre valores e índices

Hay tres formas básicas de recorrer un vector con un bucle for:

Bucle sobre los elementos: for (x in xs)
Bucle sobre los índices numéricos: for (i in seq_along(xs))
Bucle sobre los nombres: for (nm in names(xs))

La primera forma es análoga a la familia map(). Las formas segunda y tercera son equivalentes a la familia imap() que le permite iterar sobre los valores y los índices de un vector en paralelo.

imap() es como map2() en el sentido de que su .f se llama con dos argumentos, pero aquí ambos se derivan del vector. imap(x, f) es equivalente a map2(x, nombres(x), f) si x tiene nombres, y map2(x, seq_along(x), f) si no los tiene.

imap() suele ser útil para construir etiquetas:

imap_chr(iris, ~ paste0("The first value of ", .y, " is ", .x[[1]]))
#>                             Sepal.Length 
#> "The first value of Sepal.Length is 5.1" 
#>                              Sepal.Width 
#>  "The first value of Sepal.Width is 3.5" 
#>                             Petal.Length 
#> "The first value of Petal.Length is 1.4" 
#>                              Petal.Width 
#>  "The first value of Petal.Width is 0.2" 
#>                                  Species 
#>   "The first value of Species is setosa"

Si el vector no tiene nombre, el segundo argumento será el índice:

x <- map(1:6, ~ sample(1000, 10))
imap_chr(x, ~ paste0("The highest value of ", .y, " is ", max(.x)))
#> [1] "The highest value of 1 is 975" "The highest value of 2 is 915"
#> [3] "The highest value of 3 is 982" "The highest value of 4 is 955"
#> [5] "The highest value of 5 is 971" "The highest value of 6 is 696"

imap() es una ayuda útil si desea trabajar con los valores de un vector junto con sus posiciones.

9.4.5 Cualquier número de entradas: `pmap ()` y amigos

Ya que tenemos map() y map2(), podrías esperar map3(), map4(), map5(), … Pero, ¿dónde te detendrías? En lugar de generalizar map2() a un número arbitrario de argumentos, purrr adopta un rumbo ligeramente diferente con pmap(): le proporciona una sola lista, que contiene cualquier número de argumentos. En la mayoría de los casos, será una lista de vectores de igual longitud, es decir, algo muy similar a un data frame. En los diagramas, enfatizaré esa relación dibujando la entrada de forma similar a un data frame.

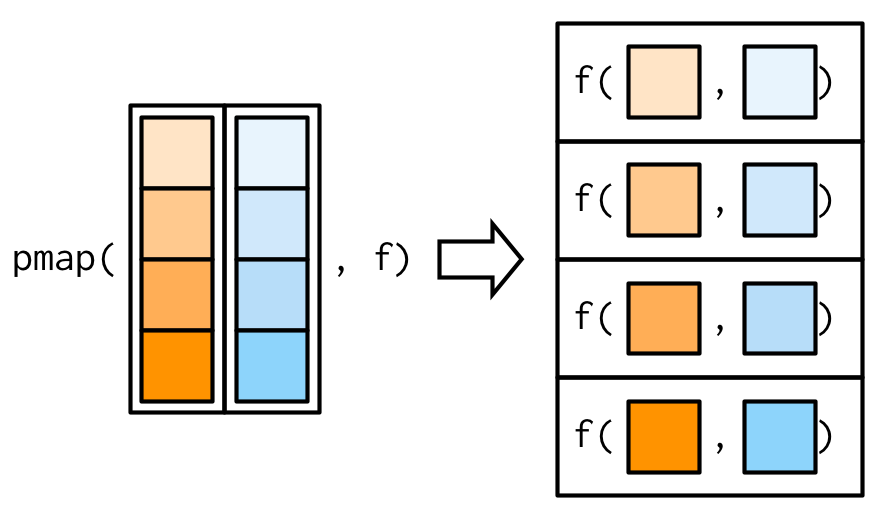
Hay una equivalencia simple entre map2() y pmap(): map2(x, y, f) es lo mismo que pmap(list(x, y), f). El pmap() equivalente a map2_dbl(xs, ws,weighted.mean) utilizado anteriormente es:

pmap_dbl(list(xs, ws), weighted.mean)
#> [1]    NA 0.451 0.603 0.452 0.563 0.510 0.342 0.464

Como antes, los argumentos variables vienen antes de .f (aunque ahora deben estar envueltos en una lista), y los argumentos constantes vienen después.

pmap_dbl(list(xs, ws), weighted.mean, na.rm = TRUE)
#> [1] 0.504 0.451 0.603 0.452 0.563 0.510 0.342 0.464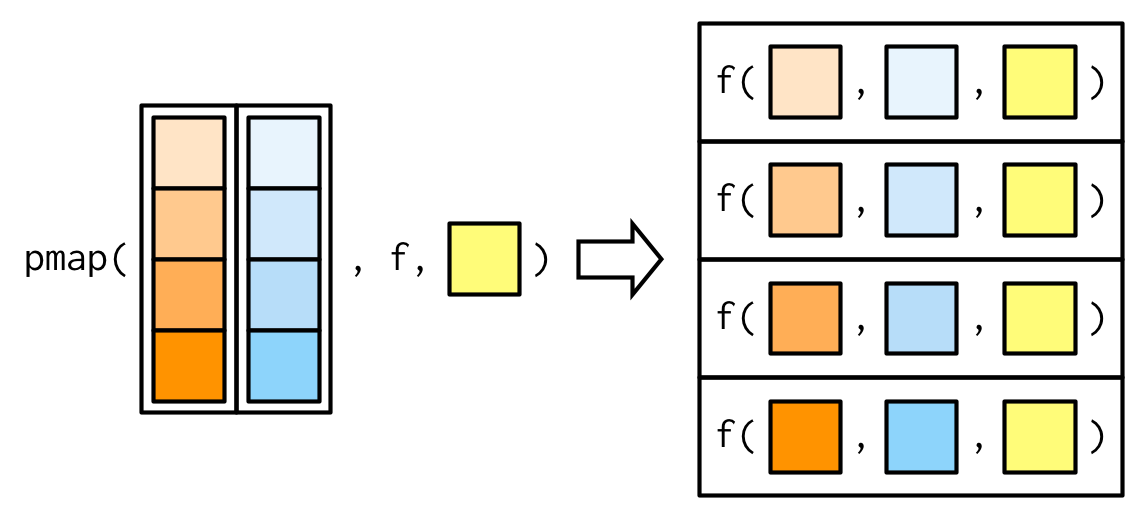

Una gran diferencia entre pmap() y las otras funciones de mapa es que pmap() te da un control mucho más preciso sobre la coincidencia de argumentos porque puedes nombrar los componentes de la lista. Volviendo a nuestro ejemplo de la Sección 9.2.5, donde queríamos cambiar el argumento trim a x, podríamos usar pmap():

trims <- c(0, 0.1, 0.2, 0.5)
x <- rcauchy(1000)

pmap_dbl(list(trim = trims), mean, x = x)
#> [1] -6.6740  0.0210  0.0235  0.0151

Creo que es una buena práctica nombrar los componentes de la lista para dejar muy claro cómo se llamará a la función.

A menudo es conveniente llamar a pmap() con un data frame. Una forma práctica de crear ese data frame es con tibble::tribble(), que le permite describir un data frame fila por fila (en lugar de columna por columna, como de costumbre): pensando en los parámetros a una función como data frame es un patrón muy poderoso. El siguiente ejemplo muestra cómo puede dibujar números uniformes aleatorios con diferentes parámetros:

params <- tibble::tribble(
  ~ n, ~ min, ~ max,
   1L,     0,     1,
   2L,    10,   100,
   3L,   100,  1000
)

pmap(params, runif)
#> [[1]]
#> [1] 0.332
#> 
#> [[2]]
#> [1] 53.5 47.6
#> 
#> [[3]]
#> [1] 231 715 515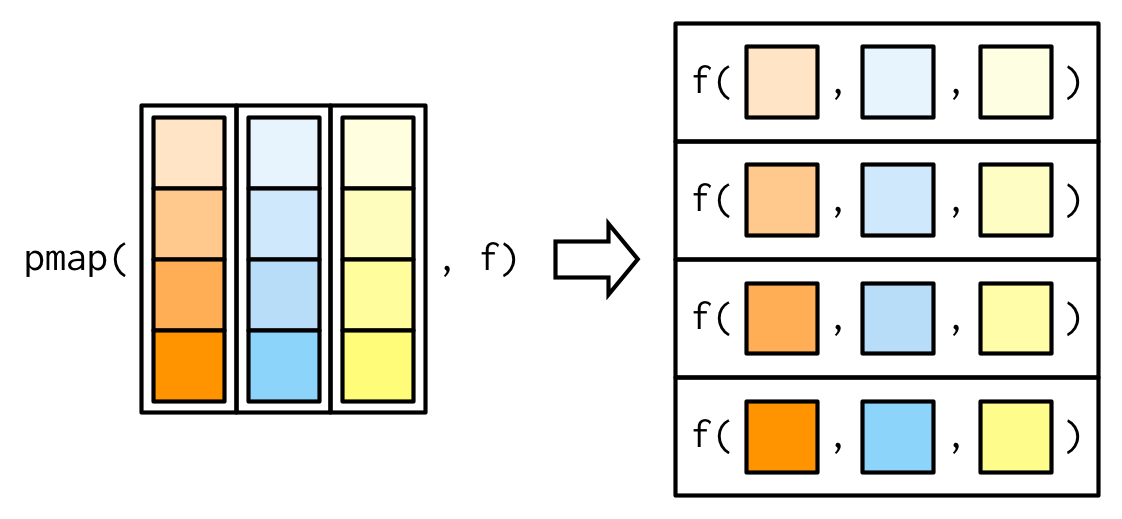

Aquí, los nombres de las columnas son fundamentales: elegí cuidadosamente hacerlos coincidir con los argumentos de runif(), por lo que pmap(params, runif) es equivalente a runif(n = 1L, min = 0, max = 1), runif(n = 2, min = 10, max = 100), runif(n = 3L, min = 100, max = 1000). (Si tiene un data frame en la mano y los nombres no coinciden, use dplyr::rename() o similar).

Hay dos equivalentes base para la familia pmap(): Map() y mapply(). Ambos tienen importantes inconvenientes:

Map() vectoriza sobre todos los argumentos para que no pueda proporcionar argumentos que no varíen.
mapply() es la versión multidimensional de sapply(); conceptualmente, toma la salida de Map() y la simplifica si es posible. Esto le da problemas similares a sapply(). No existe un equivalente de múltiples entradas de vapply().

9.4.6 Ejercicios

Explique los resultados de modify(mtcars, 1).

Reescribe el siguiente código para usar iwalk() en lugar de walk2(). ¿Cuáles son las ventajas y desventajas?

cyls <- split(mtcars, mtcars$cyl)
paths <- file.path(temp, paste0("cyl-", names(cyls), ".csv"))
walk2(cyls, paths, write.csv)

Explique cómo el siguiente código transforma un data frame utilizando funciones almacenadas en una lista.

trans <- list(
  disp = function(x) x * 0.0163871,
  am = function(x) factor(x, labels = c("auto", "manual"))
)

nm <- names(trans)
mtcars[nm] <- map2(trans, mtcars[nm], function(f, var) f(var))

Compare y contraste el enfoque map2() con este enfoque map():

mtcars[nm] <- map(nm, ~ trans[[.x]](mtcars[[.x]]))

¿Qué devuelve write.csv(), es decir, qué sucede si lo usa con map2() en lugar de walk2()?

9.5 Familia reduce

Después de la familia map, la siguiente familia de funciones más importante es la familia reduce. Esta familia es mucho más pequeña, con solo dos variantes principales, y se usa con menos frecuencia, pero es una idea poderosa, nos brinda la oportunidad de analizar algo de álgebra útil y potencia el marco de reducción de mapas que se usa con frecuencia para procesar conjuntos de datos muy grandes.

9.5.1 Lo esencial

reduce() toma un vector de longitud n y produce un vector de longitud 1 llamando a una función con un par de valores a la vez: reduce(1:4, f) es equivalente a f(f(f(1, 2), 3), 4).

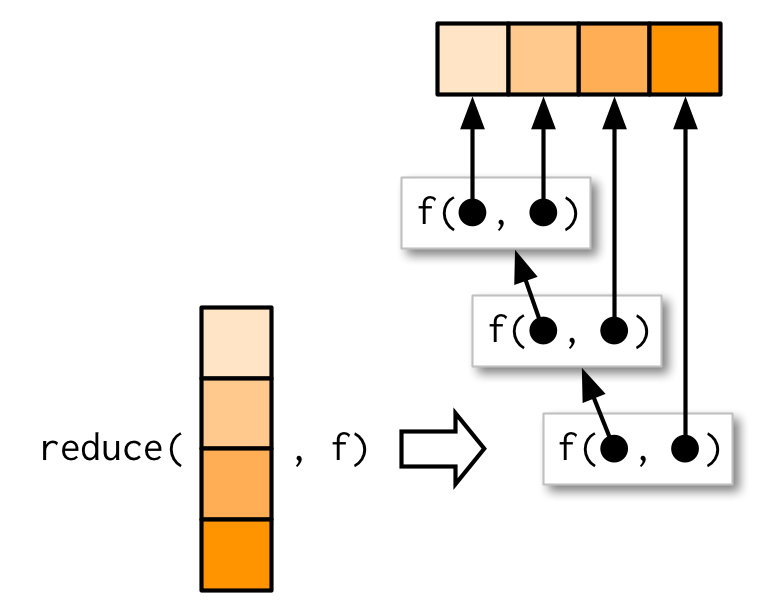
reduce() es una forma útil de generalizar una función que funciona con dos entradas (una función binaria) para que funcione con cualquier cantidad de entradas. Imagina que tienes una lista de vectores numéricos y quieres encontrar los valores que ocurren en cada elemento. Primero generamos algunos datos de muestra:

l <- map(1:4, ~ sample(1:10, 15, replace = T))
str(l)
#> List of 4
#>  $ : int [1:15] 7 1 8 8 3 8 2 4 7 10 ...
#>  $ : int [1:15] 3 1 10 2 5 2 9 8 5 4 ...
#>  $ : int [1:15] 6 10 9 5 6 7 8 6 10 8 ...
#>  $ : int [1:15] 9 8 6 4 4 5 2 9 9 6 ...

Para resolver este desafío necesitamos usar intersect() repetidamente:

out <- l[[1]]
out <- intersect(out, l[[2]])
out <- intersect(out, l[[3]])
out <- intersect(out, l[[4]])
out
#> [1] 8 4

reduce() Automatiza esta solución para nosotros, para que podamos escribir:

reduce(l, intersect)
#> [1] 8 4

Podríamos aplicar la misma idea si quisiéramos listar todos los elementos que aparecen en al menos una entrada. Todo lo que tenemos que hacer es cambiar de intersect() a union():

reduce(l, union)
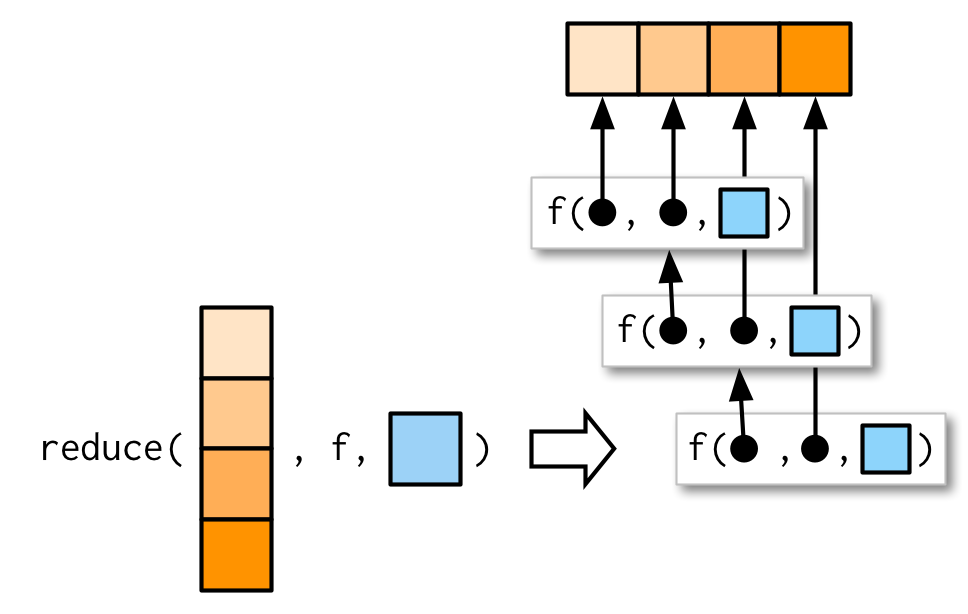
#>  [1]  7  1  8  3  2  4 10  5  9  6

Al igual que la familia de mapas, también puede pasar argumentos adicionales. intersect() y union() no aceptan argumentos adicionales, así que no puedo demostrarlos aquí, pero el principio es sencillo y le hice un dibujo.

Como de costumbre, la esencia de reduce() se puede reducir a un simple envoltorio alrededor de un bucle for:

simple_reduce <- function(x, f) {
  out <- x[[1]]
  for (i in seq(2, length(x))) {
    out <- f(out, x[[i]])
  }
  out
}

El equivalente básico es Reduce(). Tenga en cuenta que el orden de los argumentos es diferente: la función viene primero, seguida del vector, y no hay forma de proporcionar argumentos adicionales.

9.5.2 accumulate

La primera variante reduce(), accumulate(), es útil para comprender cómo funciona reduce, porque en lugar de devolver solo el resultado final, también devuelve todos los resultados intermedios:

accumulate(l, intersect)
#> [[1]]
#>  [1]  7  1  8  8  3  8  2  4  7 10 10  3  7 10 10
#> 
#> [[2]]
#> [1]  1  8  3  2  4 10
#> 
#> [[3]]
#> [1]  8  4 10
#> 
#> [[4]]
#> [1] 8 4

Otra forma útil de entender reduce es pensar en sum(): sum(x) es equivalente a x[[1]] + x[[2]] + x[[3]] + ..., es decir reduce(x, `+`). Entonces accumulate(x, `+`) es la suma acumulada:

x <- c(4, 3, 10)
reduce(x, `+`)
#> [1] 17

accumulate(x, `+`)
#> [1]  4  7 17

9.5.3 Tipos de salida

En el ejemplo anterior usando +, ¿qué debería devolver reduce() cuando x es corto, es decir, longitud 1 o 0? Sin argumentos adicionales, reduce() solo devuelve la entrada cuando x tiene una longitud de 1:

reduce(1, `+`)
#> [1] 1

Esto significa que reduce() no tiene forma de verificar que la entrada sea válida:

reduce("a", `+`)
#> [1] "a"

¿Qué pasa si es de longitud 0? Recibimos un error que sugiere que necesitamos usar el argumento .init:

reduce(integer(), `+`)
#> Error in `reduce()`:
#> ! Must supply `.init` when `.x` is empty.

¿Qué debería ser .init aquí? Para averiguarlo, necesitamos ver qué sucede cuando se proporciona .init:

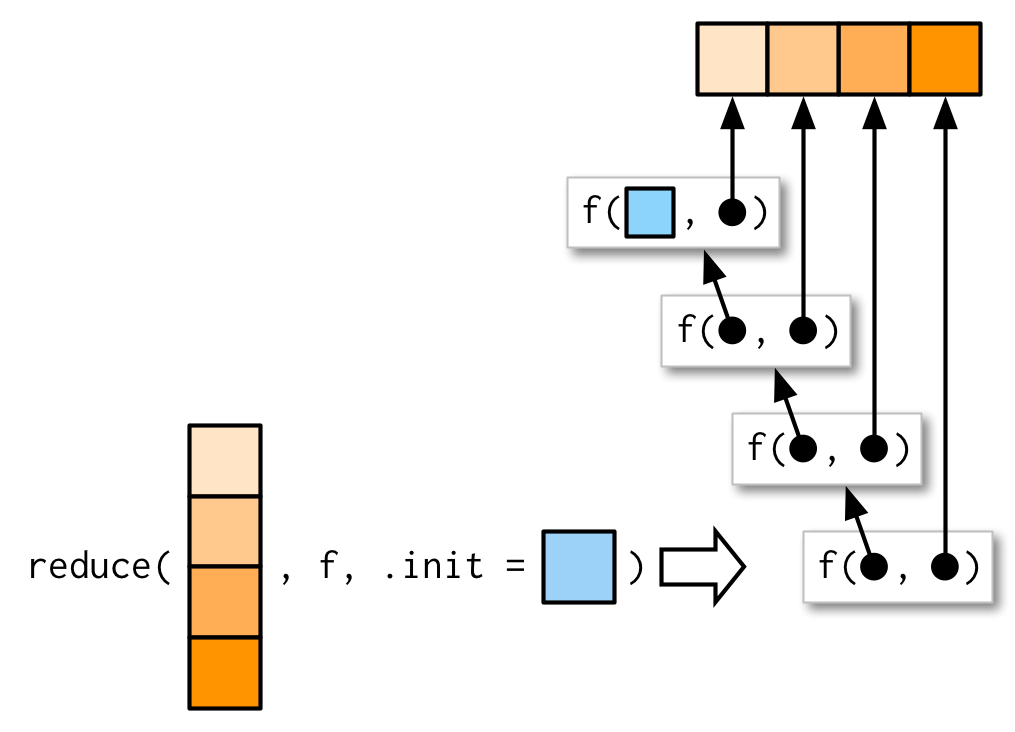
Así que si llamamos a reduce(1, `+`, init) el resultado será `1 + init. Ahora sabemos que el resultado debería ser solo 1, lo que sugiere que .init debería ser 0:

reduce(integer(), `+`, .init = 0)
#> [1] 0

Esto también asegura que reduce() verifique que las entradas de longitud 1 sean válidas para la función que estás llamando:

reduce("a", `+`, .init = 0)
#> Error in .x + .y: non-numeric argument to binary operator

Si quieres ser algebraico al respecto, 0 se llama la identidad de los números reales en la operación de suma: si agregas un 0 a cualquier número, obtienes el mismo número. R aplica el mismo principio para determinar qué debe devolver una función de resumen con una entrada de longitud cero:

sum(integer())  # x + 0 = x
#> [1] 0
prod(integer()) # x * 1 = x
#> [1] 1
min(integer())  # min(x, Inf) = x
#> [1] Inf
max(integer())  # max(x, -Inf) = x
#> [1] -Inf

Si está utilizando reduce() en una función, siempre debe proporcionar .init. Piense detenidamente qué debe devolver su función cuando pasa un vector de longitud 0 o 1, y asegúrese de probar su implementación.

9.5.4 Múltiples entradas

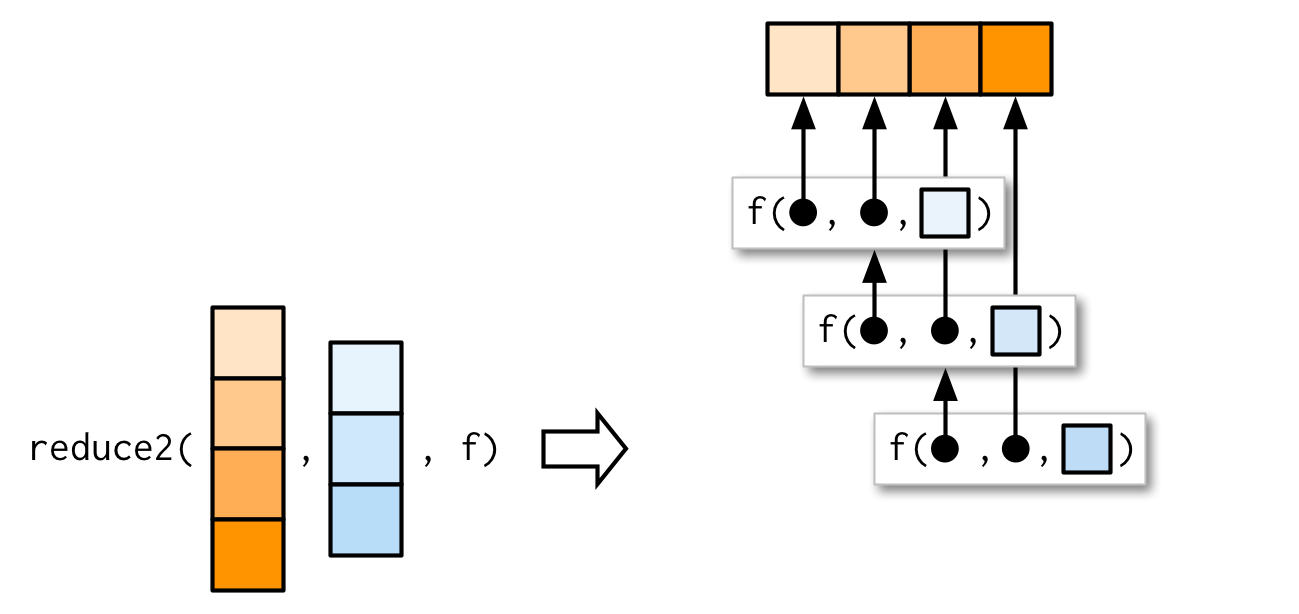
Muy ocasionalmente necesita pasar dos argumentos a la función que está reduciendo. Por ejemplo, puede tener una lista de data frames que desea unir y las variables que usa para unir variarán de un elemento a otro. Este es un escenario muy especializado, por lo que no quiero dedicarle mucho tiempo, pero sí quiero que sepas que reduce2() existe.

La longitud del segundo argumento varía en función de si se proporciona .init o no: si tiene cuatro elementos de x, f solo se llamará tres veces. Si proporciona init, f se llamará cuatro veces.

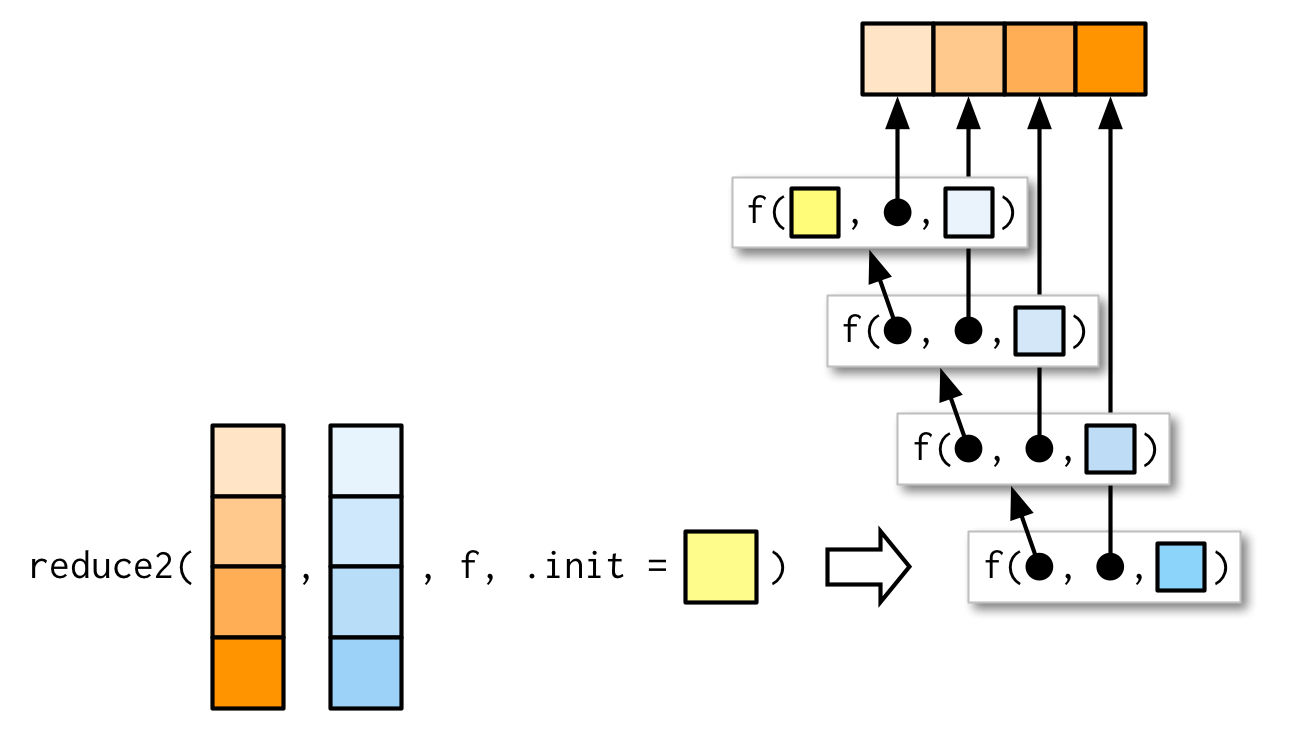
9.5.5 Mapa reducido

Es posible que haya oído hablar de map-reduce, la idea que impulsa la tecnología como Hadoop. Ahora puedes ver cuán simple y poderosa es la idea subyacente: map-reduce es un mapa combinado con una reducción. La diferencia para los datos grandes es que los datos se distribuyen en varias computadoras. Cada computadora realiza el mapa en los datos que tiene, luego envía el resultado a un coordinador que reduce los resultados individuales a un solo resultado.

Como un ejemplo simple, imagine calcular la media de un vector muy grande, tan grande que tiene que dividirse entre varias computadoras. Puede pedirle a cada computadora que calcule la suma y la longitud, y luego devolverlos al coordinador que calcula la media general dividiendo la suma total por la longitud total.

9.6 Funcionales de predicado

Un predicado es una función que devuelve un solo TRUE o FALSE, como is.character(), is.null() o all(), y decimos un predicado coincide con un vector si devuelve TRUE.

9.6.1 Lo esencial

Un predicado funcional aplica un predicado a cada elemento de un vector. purrr proporciona siete funciones útiles que se dividen en tres grupos:

some(.x, .p) devuelve TRUE si algún elemento coincide;
every(.x, .p) devuelve TRUE si todos los elementos coinciden;
none(.x, .p) devuelve TRUE si ningún elemento coincide.

Estos son similares a any(map_lgl(.x, .p)), all(map_lgl(.x, .p)) y all(map_lgl(.x, negate(.p))) pero terminar antes de tiempo: some() devuelve TRUE cuando ve el primer TRUE, y cada() y ninguno() devuelve FALSE cuando ven el primer FALSE o TRUE respectivamente .
detect(.x, .p) devuelve el valor de la primera coincidencia; detect_index(.x, .p) devuelve la ubicación de la primera coincidencia.
keep(.x, .p) mantiene todos los elementos coincidentes; discard(.x, .p) suelta todos los elementos coincidentes.

El siguiente ejemplo muestra cómo puede usar estas funciones con un data frame:

df <- data.frame(x = 1:3, y = c("a", "b", "c"))
detect(df, is.factor)
#> NULL
detect_index(df, is.factor)
#> [1] 0

str(keep(df, is.factor))
#> 'data.frame':    3 obs. of  0 variables
str(discard(df, is.factor))
#> 'data.frame':    3 obs. of  2 variables:
#>  $ x: int  1 2 3
#>  $ y: chr  "a" "b" "c"

9.6.2 Variantes de map

map() y modify() vienen en variantes que también toman funciones de predicado, transformando solo los elementos de .x donde .p es TRUE.

df <- data.frame(
  num1 = c(0, 10, 20),
  num2 = c(5, 6, 7),
  chr1 = c("a", "b", "c"),
  stringsAsFactors = FALSE
)

str(map_if(df, is.numeric, mean))
#> List of 3
#>  $ num1: num 10
#>  $ num2: num 6
#>  $ chr1: chr [1:3] "a" "b" "c"
str(modify_if(df, is.numeric, mean))
#> 'data.frame':    3 obs. of  3 variables:
#>  $ num1: num  10 10 10
#>  $ num2: num  6 6 6
#>  $ chr1: chr  "a" "b" "c"
str(map(keep(df, is.numeric), mean))
#> List of 2
#>  $ num1: num 10
#>  $ num2: num 6

9.6.3 Ejercicios

¿Por qué is.na() no es una función de predicado? ¿Qué función base de R está más cerca de ser una versión predicada de is.na()?

simple_reduce() tiene un problema cuando x tiene una longitud de 0 o de 1. Describa el origen del problema y cómo podría solucionarlo.

simple_reduce <- function(x, f) {
  out <- x[[1]]
  for (i in seq(2, length(x))) {
    out <- f(out, x[[i]])
  }
  out
}

Implemente la función span() de Haskell: dada una lista x y una función de predicado f, span(x, f) devuelve la ubicación de la ejecución secuencial más larga de elementos donde el predicado es verdadero. (Sugerencia: puede encontrar útil rle()).
Implementar arg_max(). Debe tomar una función y un vector de entradas, y devolver los elementos de la entrada donde la función devuelve el valor más alto. Por ejemplo, arg_max(-10:5, function(x) x ^ 2) debería devolver -10. arg_max(-5:5, function(x) x ^ 2) debería devolver c(-5, 5). Implemente también la función coincidente arg_min().
La siguiente función escala un vector para que caiga en el rango [0, 1]. ¿Cómo lo aplicaría a cada columna de un data frame? ¿Cómo lo aplicaría a cada columna numérica en un data frame?
```
scale01 <- function(x) {
  rng <- range(x, na.rm = TRUE)
  (x - rng[1]) / (rng[2] - rng[1])
}
```

9.7 Funcionales base

Para terminar el capítulo, aquí ofrezco un resumen de importantes funciones base que no son miembros de las familias map, reduce o predicate y, por lo tanto, no tienen equivalente en purrr. Esto no quiere decir que no sean importantes, pero tienen un sabor más matemático o estadístico y, en general, son menos útiles en el análisis de datos.

9.7.1 Matrices y arreglos

map() y amigos están especializados para trabajar con vectores unidimensionales. base::apply() está especializado para trabajar con vectores bidimensionales y superiores, es decir, matrices y arreglos. Puede pensar en apply() como una operación que resume una matriz o conjunto al colapsar cada fila o columna en un solo valor. Tiene cuatro argumentos:

X, la matriz o arreglo para resumir.
MARGIN, un vector entero que da las dimensiones para resumir, 1 = filas, 2 = columnas, etc. (El nombre del argumento proviene de pensar en los márgenes de una distribución conjunta).
FUN, una función de resumen.
... otros argumentos pasan a FUN.

Un ejemplo típico de apply() se ve así

a2d <- matrix(1:20, nrow = 5)
apply(a2d, 1, mean)
#> [1]  8.5  9.5 10.5 11.5 12.5
apply(a2d, 2, mean)
#> [1]  3  8 13 18

Puede especificar múltiples dimensiones para MARGIN, lo cual es útil para arreglos de alta dimensión:

a3d <- array(1:24, c(2, 3, 4))
apply(a3d, 1, mean)
#> [1] 12 13
apply(a3d, c(1, 2), mean)
#>      [,1] [,2] [,3]
#> [1,]   10   12   14
#> [2,]   11   13   15

Hay dos advertencias para usar apply():

Al igual que base::sapply(), no tienes control sobre el tipo de salida; se simplificará automáticamente a una lista, matriz o vector. Sin embargo, generalmente usa apply() con matrices numéricas y una función de resumen numérico, por lo que es menos probable que encuentre un problema que con sapply().
apply() tampoco es idempotente en el sentido de que si la función de resumen es el operador de identidad, la salida no siempre es la misma que la entrada.
```
a1 <- apply(a2d, 1, identity)
identical(a2d, a1)
#> [1] FALSE

a2 <- apply(a2d, 2, identity)
identical(a2d, a2)
#> [1] TRUE
```

Nunca uses apply() con un data frame. Siempre lo obliga a una matriz, lo que conducirá a resultados no deseados si su data frame contiene algo más que números.

df <- data.frame(x = 1:3, y = c("a", "b", "c"))
apply(df, 2, mean)
#> Warning in mean.default(newX[, i], ...): argument is not numeric or logical:
#> returning NA
#> Warning in mean.default(newX[, i], ...): argument is not numeric or logical:
#> returning NA
#>  x  y 
#> NA NA

9.7.2 Preocupaciones matemáticas

Los funcionales son muy comunes en matemáticas. El límite, el máximo, las raíces (el conjunto de puntos donde f(x) = 0) y la integral definida son todos funcionales: dada una función, devuelven un solo número (o vector de números). A primera vista, estas funciones no parecen encajar con el tema de la eliminación de bucles, pero si profundiza, descubrirá que todas se implementan mediante un algoritmo que implica iteración.

Base R proporciona un conjunto útil:

integrate() encuentra el área bajo la curva definida por f()
uniroot() encuentra donde f() llega a cero
optimise() encuentra la ubicación del valor más bajo (o más alto) de f()

El siguiente ejemplo muestra cómo se pueden usar los funcionales con una función simple, sin():

integrate(sin, 0, pi)
#> 2 with absolute error < 2.2e-14
str(uniroot(sin, pi * c(1 / 2, 3 / 2)))
#> List of 5
#>  $ root      : num 3.14
#>  $ f.root    : num 1.22e-16
#>  $ iter      : int 2
#>  $ init.it   : int NA
#>  $ estim.prec: num 6.1e-05
str(optimise(sin, c(0, 2 * pi)))
#> List of 2
#>  $ minimum  : num 4.71
#>  $ objective: num -1
str(optimise(sin, c(0, pi), maximum = TRUE))
#> List of 2
#>  $ maximum  : num 1.57
#>  $ objective: num 1

9.7.3 Ejercicios

¿Cómo organiza apply() la salida? Lea la documentación y realice algunos experimentos.
¿Qué hacen eapply() y rapply()? ¿En purrr tiene equivalentes?
Desafío: lea sobre el algoritmo de punto fijo. Completa los ejercicios usando R.

En resumen, los valores invisibles solo se imprimen si lo solicita explícitamente. Esto los hace muy adecuados para las funciones llamadas principalmente por sus efectos secundarios, ya que permite ignorar su salida de forma predeterminada, al tiempo que ofrece una opción para capturarla. Ver Sección 6.7.2 para más detalles.↩︎