13  Números

13.1 Introducción

Los vectores numéricos son la columna vertebral de la ciencia de datos y ya los ha usado varias veces anteriormente en el libro. Ahora es el momento de examinar sistemáticamente lo que puede hacer con ellos en R, asegurándose de estar bien situado para abordar cualquier problema futuro que involucre vectores numéricos.

Comenzaremos brindándole un par de herramientas para hacer números si tiene cadenas, y luego entraremos en un poco más de detalle de count(). Luego nos sumergiremos en varias transformaciones numéricas que combinan bien con mutate(), incluidas transformaciones más generales que se pueden aplicar a otros tipos de vectores, pero que a menudo se usan con vectores numéricos. Terminaremos cubriendo las funciones de resumen que combinan bien con summarize() y le mostraremos cómo también se pueden usar con mutate().

13.1.1 Requisitos previos

Este capítulo utiliza principalmente funciones de base R, que están disponibles sin cargar ningún paquete. Pero aún necesitamos el tidyverse porque usaremos estas funciones básicas de R dentro de las funciones de tidyverse como mutate() y filter(). Como en el último capítulo, usaremos ejemplos reales de nycflights13, así como ejemplos de juguetes hechos con c() y tribble().

library(tidyverse)
library(nycflights13)

13.2 Haciendo úmeros

En la mayoría de los casos, obtendrá números ya registrados en uno de los tipos numéricos de R: entero o doble. En algunos casos, sin embargo, los encontrará como cadenas, posiblemente porque los creó al girar desde los encabezados de columna o porque algo salió mal en su proceso de importación de datos.

readr proporciona dos funciones útiles para analizar cadenas en números: parse_double() y parse_number(). Usa parse_double() cuando tengas números escritos como cadenas:

x <- c("1.2", "5.6", "1e3")
parse_double(x)
#> [1]    1.2    5.6 1000.0

Usa parse_number() cuando la cadena contenga texto no numérico que quieras ignorar. Esto es particularmente útil para datos de moneda y porcentajes:

x <- c("$1,234", "USD 3,513", "59%")
parse_number(x)
#> [1] 1234 3513   59

13.3 Contar

Es sorprendente la cantidad de ciencia de datos que puede hacer con solo conteos y un poco de aritmética básica, por lo que dplyr se esfuerza por hacer que contar sea lo más fácil posible con count(). Esta función es excelente para realizar exploraciones y comprobaciones rápidas durante el análisis:

flights |> count(dest)
#> # A tibble: 105 × 2
#>   dest      n
#>   <chr> <int>
#> 1 ABQ     254
#> 2 ACK     265
#> 3 ALB     439
#> 4 ANC       8
#> 5 ATL   17215
#> 6 AUS    2439
#> # ℹ 99 more rows

(A pesar de los consejos en Capítulo 4, generalmente colocamos count() en una sola línea porque generalmente se usa en la consola para verificar rápidamente que un cálculo funciona como se esperaba.)

Si desea ver los valores más comunes, agregue sort = TRUE:

flights |> count(dest, sort = TRUE)
#> # A tibble: 105 × 2
#>   dest      n
#>   <chr> <int>
#> 1 ORD   17283
#> 2 ATL   17215
#> 3 LAX   16174
#> 4 BOS   15508
#> 5 MCO   14082
#> 6 CLT   14064
#> # ℹ 99 more rows

Y recuerda que si quieres ver todos los valores, puedes usar |> View() o |> print(n = Inf).

Puede realizar el mismo cálculo “a mano” con group_by(), summarize() y n(). Esto es útil porque le permite calcular otros resúmenes al mismo tiempo:

flights |> 
  group_by(dest) |> 
  summarize(
    n = n(),
    delay = mean(arr_delay, na.rm = TRUE)
  )
#> # A tibble: 105 × 3
#>   dest      n delay
#>   <chr> <int> <dbl>
#> 1 ABQ     254  4.38
#> 2 ACK     265  4.85
#> 3 ALB     439 14.4 
#> 4 ANC       8 -2.5 
#> 5 ATL   17215 11.3 
#> 6 AUS    2439  6.02
#> # ℹ 99 more rows

n() es una función de resumen especial que no toma ningún argumento y en su lugar accede a información sobre el grupo “actual”. Esto significa que solo funciona dentro de los verbos dplyr:

n()
#> Error in `n()`:
#> ! Must only be used inside data-masking verbs like `mutate()`,
#>   `filter()`, and `group_by()`.

Hay un par de variantes de n() y count() que pueden resultarle útiles:

• n_distinct(x) cuenta el número de valores distintos (únicos) de una o más variables. Por ejemplo, podríamos averiguar qué destinos son atendidos por la mayoría de los transportistas:

  flights |> 
    group_by(dest) |> 
    summarize(carriers = n_distinct(carrier)) |> 
    arrange(desc(carriers))
  #> # A tibble: 105 × 2
  #>   dest  carriers
  #>   <chr>    <int>
  #> 1 ATL          7
  #> 2 BOS          7
  #> 3 CLT          7
  #> 4 ORD          7
  #> 5 TPA          7
  #> 6 AUS          6
  #> # ℹ 99 more rows

• Una cuenta ponderada es una suma. Por ejemplo, podría “contar” el número de millas que voló cada avión:

  flights |> 
    group_by(tailnum) |> 
    summarize(miles = sum(distance))
  #> # A tibble: 4,044 × 2
  #>   tailnum  miles
  #>   <chr>    <dbl>
  #> 1 D942DN    3418
  #> 2 N0EGMQ  250866
  #> 3 N10156  115966
  #> 4 N102UW   25722
  #> 5 N103US   24619
  #> 6 N104UW   25157
  #> # ℹ 4,038 more rows

  Los recuentos ponderados son un problema común, por lo que count() tiene un argumento wt que hace lo mismo:

  flights |> count(tailnum, wt = distance)

• Puede contar los valores perdidos combinando sum() y is.na(). En el conjunto de datos de flights, esto representa los vuelos que se cancelan:

  flights |> 
    group_by(dest) |> 
    summarize(n_cancelled = sum(is.na(dep_time))) 
  #> # A tibble: 105 × 2
  #>   dest  n_cancelled
  #>   <chr>       <int>
  #> 1 ABQ             0
  #> 2 ACK             0
  #> 3 ALB            20
  #> 4 ANC             0
  #> 5 ATL           317
  #> 6 AUS            21
  #> # ℹ 99 more rows

13.3.1 Ejercicios

1. ¿Cómo puedes usar count() para contar las el número de filas con un valor faltante para una variable dada?
2. Expanda las siguientes llamadas a count() para usar en su lugar group_by(), summarize() y arrange():

   1. flights |> count(dest, sort = TRUE)

   2. flights |> count(tailnum, wt = distance)

13.4 Transformaciones numéricas

Las funciones de transformación funcionan bien con mutate() porque su salida tiene la misma longitud que la entrada. La gran mayoría de las funciones de transformación ya están integradas en la base R. No es práctico enumerarlos todos, por lo que esta sección mostrará los más útiles. Como ejemplo, aunque R proporciona todas las funciones trigonométricas con las que podría soñar, no las enumeramos aquí porque rara vez se necesitan para la ciencia de datos.

13.4.1 Reglas aritméticas y de reciclaje.

Introdujimos los conceptos básicos de aritmética (+, -, *, /, ^) en Capítulo 2 y los hemos usado mucho desde entonces. Estas funciones no necesitan una gran cantidad de explicación porque hacen lo que aprendiste en la escuela primaria. Pero necesitamos hablar brevemente sobre las reglas de reciclaje que determinan lo que sucede cuando los lados izquierdo y derecho tienen diferentes longitudes. Esto es importante para operaciones como flights |> mutate(air_time = air_time / 60) porque hay 336.776 números a la izquierda de / pero solo uno a la derecha.

R maneja las longitudes que no coinciden reciclando o repitiendo el vector corto. Podemos ver esto en funcionamiento más fácilmente si creamos algunos vectores fuera de un data frame:

x <- c(1, 2, 10, 20)
x / 5
#> [1] 0.2 0.4 2.0 4.0
# is shorthand for
x / c(5, 5, 5, 5)
#> [1] 0.2 0.4 2.0 4.0

En general, solo desea reciclar números individuales (es decir, vectores de longitud 1), pero R reciclará cualquier vector de longitud más corta. Por lo general (pero no siempre) le da una advertencia si el vector más largo no es un múltiplo del más corto:

x * c(1, 2)
#> [1]  1  4 10 40
x * c(1, 2, 3)
#> Warning in x * c(1, 2, 3): longer object length is not a multiple of shorter
#> object length
#> [1]  1  4 30 20

Estas reglas de reciclaje también se aplican a las comparaciones lógicas (==, <, <=, >, >=, !=) y pueden conducir a un resultado sorprendente si accidentalmente usa == en lugar de %in% y el data frame tiene un número desafortunado de filas. Por ejemplo, tome este código que intenta encontrar todos los vuelos en enero y febrero:

flights |> 
  filter(month == c(1, 2))
#> # A tibble: 25,977 × 19
#>    year month   day dep_time sched_dep_time dep_delay arr_time sched_arr_time
#>   <int> <int> <int>    <int>          <int>     <dbl>    <int>          <int>
#> 1  2013     1     1      517            515         2      830            819
#> 2  2013     1     1      542            540         2      923            850
#> 3  2013     1     1      554            600        -6      812            837
#> 4  2013     1     1      555            600        -5      913            854
#> 5  2013     1     1      557            600        -3      838            846
#> 6  2013     1     1      558            600        -2      849            851
#> # ℹ 25,971 more rows
#> # ℹ 11 more variables: arr_delay <dbl>, carrier <chr>, flight <int>, …

El código se ejecuta sin errores, pero no devuelve lo que desea. Debido a las reglas de reciclaje, encuentra vuelos en filas impares que partieron en enero y vuelos en filas pares que partieron en febrero. Y, lamentablemente, no hay ninguna advertencia porque flights tiene un número par de filas.

Para protegerlo de este tipo de fallas silenciosas, la mayoría de las funciones de tidyverse utilizan una forma más estricta de reciclaje que solo recicla valores únicos. Desafortunadamente, eso no ayuda aquí, ni en muchos otros casos, porque el cálculo clave lo realiza la función base R ==, no filter().

13.4.2 Mínimo y máximo

Las funciones aritméticas trabajan con pares de variables. Dos funciones estrechamente relacionadas son pmin() y pmax(), que cuando se les dan dos o más variables devolverán el valor más pequeño o más grande en cada fila:

df <- tribble(
  ~x, ~y,
  1,  3,
  5,  2,
  7, NA,
)

df |> 
  mutate(
    min = pmin(x, y, na.rm = TRUE),
    max = pmax(x, y, na.rm = TRUE)
  )
#> # A tibble: 3 × 4
#>       x     y   min   max
#>   <dbl> <dbl> <dbl> <dbl>
#> 1     1     3     1     3
#> 2     5     2     2     5
#> 3     7    NA     7     7

Tenga en cuenta que estas son diferentes a las funciones de resumen min() y max() que toman múltiples observaciones y devuelven un solo valor. Puedes darte cuenta de que has usado la forma incorrecta cuando todos los mínimos y todos los máximos tienen el mismo valor:

df |> 
  mutate(
    min = min(x, y, na.rm = TRUE),
    max = max(x, y, na.rm = TRUE)
  )
#> # A tibble: 3 × 4
#>       x     y   min   max
#>   <dbl> <dbl> <dbl> <dbl>
#> 1     1     3     1     7
#> 2     5     2     1     7
#> 3     7    NA     1     7

13.4.3 Aritmética modular

La aritmética modular es el nombre técnico del tipo de matemática que hacías antes de aprender sobre los lugares decimales, es decir, la división que produce un número entero y un resto. En R, %/% realiza la división de enteros y %% calcula el resto:

1:10 %/% 3
#>  [1] 0 0 1 1 1 2 2 2 3 3
1:10 %% 3
#>  [1] 1 2 0 1 2 0 1 2 0 1

La aritmética modular es útil para el conjunto de datos flights, porque podemos usarla para desempaquetar la variable sched_dep_time en hour y minute:

flights |> 
  mutate(
    hour = sched_dep_time %/% 100,
    minute = sched_dep_time %% 100,
    .keep = "used"
  )
#> # A tibble: 336,776 × 3
#>   sched_dep_time  hour minute
#>            <int> <dbl>  <dbl>
#> 1            515     5     15
#> 2            529     5     29
#> 3            540     5     40
#> 4            545     5     45
#> 5            600     6      0
#> 6            558     5     58
#> # ℹ 336,770 more rows

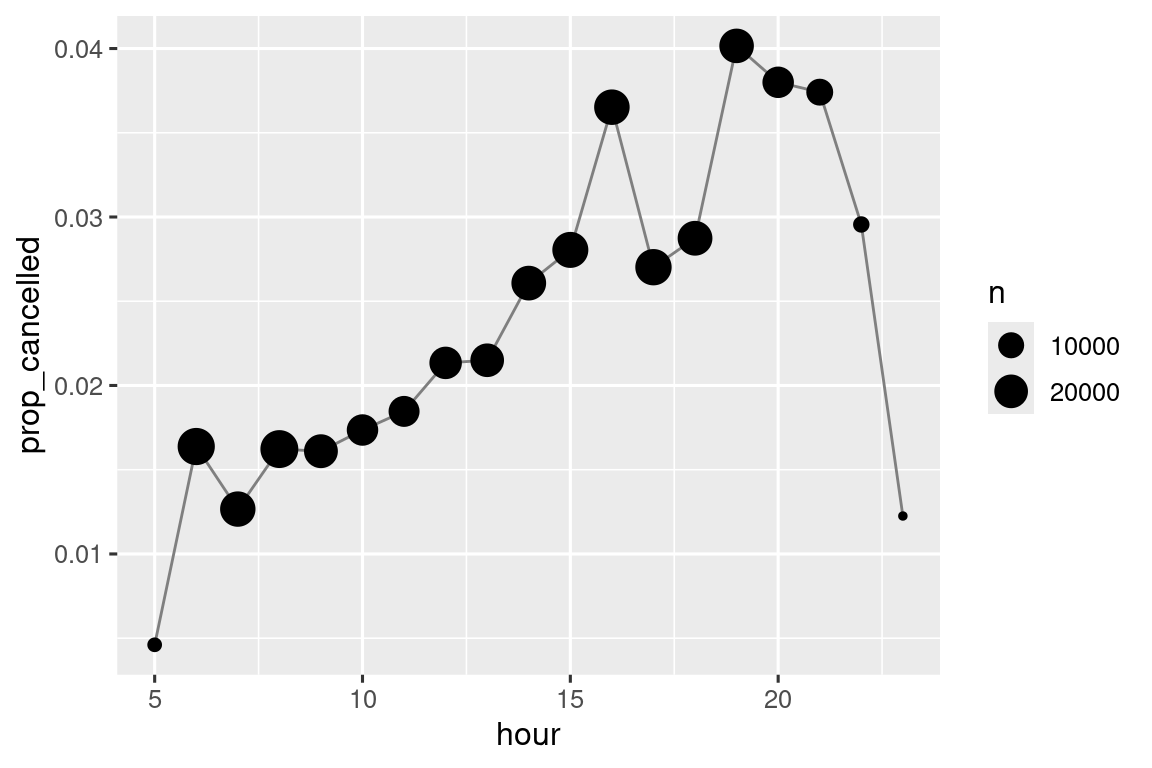
Podemos combinar eso con el truco mean(is.na(x)) de Sección 12.4 para ver cómo varía la proporción de vuelos cancelados a lo largo del día. Los resultados se muestran en Figura 13.1.

flights |> 
  group_by(hour = sched_dep_time %/% 100) |> 
  summarize(prop_cancelled = mean(is.na(dep_time)), n = n()) |> 
  filter(hour > 1) |> 
  ggplot(aes(x = hour, y = prop_cancelled)) +
  geom_line(color = "grey50") + 
  geom_point(aes(size = n))

Figura 13.1: Un gráfico de líneas con la hora de salida programada en el eje x y la proporción de vuelos cancelados en el eje y. Las cancelaciones parecen acumularse en el transcurso del día hasta las 8:00 p. m., los vuelos muy tardíos son mucho menos probables de ser cancelado.

13.4.4 Logaritmos

Los logaritmos son una transformación increíblemente útil para manejar datos que varían en varios órdenes de magnitud y convertir el crecimiento exponencial en crecimiento lineal. En R, puede elegir entre tres logaritmos: log() (el logaritmo natural, base e), log2() (base 2) y log10() (base 10). Recomendamos usar log2() o log10(). log2() es fácil de interpretar porque una diferencia de 1 en la escala logarítmica corresponde a duplicar la escala original y una diferencia de -1 corresponde a reducir a la mitad; mientras que log10() es fácil de transformar porque (por ejemplo) 3 es 10^3 = 1000. El inverso de log() es exp(); para calcular el inverso de log2() o log10() necesitará usar 2^ o 10^.

13.4.5 Redondeo

Usa round(x) para redondear un número al entero más cercano:

round(123.456)
#> [1] 123

Puede controlar la precisión del redondeo con el segundo argumento dígitos, digits. round(x, digits) se redondea al 10^-n más cercano, por lo que digits = 2 se redondea al 0,01 más cercano. Esta definición es útil porque implica que round(x, -3) se redondeará al millar más cercano, lo que de hecho sucede:

round(123.456, 2)  # dos dígitos
#> [1] 123.46
round(123.456, 1)  # un dígito
#> [1] 123.5
round(123.456, -1) # redondear a la decena más cercana
#> [1] 120
round(123.456, -2) # redondear a la centena más cercana
#> [1] 100

Hay una rareza con round() que parece sorprendente a primera vista:

round(c(1.5, 2.5))
#> [1] 2 2

round() utiliza lo que se conoce como “redondear la mitad a par” o redondeo bancario: si un número está a medio camino entre dos enteros, se redondeará al entero par. Esta es una buena estrategia porque mantiene el redondeo imparcial: la mitad de todos los 0,5 se redondean hacia arriba y la otra mitad hacia abajo.

round() se empareja con floor() que siempre redondea hacia abajo y ceiling() que siempre redondea hacia arriba:

x <- 123.456

floor(x)
#> [1] 123
ceiling(x)
#> [1] 124

Estas funciones no tienen un argumento dígitos, digits, por lo que puede reducir, redondear y luego volver a aumentar:

# Redondear hacia abajo a los dos dígitos más cercanos
floor(x / 0.01) * 0.01
#> [1] 123.45
# Redondea hacia arriba a los dos dígitos más cercanos
ceiling(x / 0.01) * 0.01
#> [1] 123.46

Puedes usar la misma técnica si quieres round() a un múltiplo de algún otro número:

# Redondea al múltiplo más cercano de 4
round(x / 4) * 4
#> [1] 124

# Redondear al 0,25 más cercano
round(x / 0.25) * 0.25
#> [1] 123.5

13.4.6 Cortar números en rangos

Use cut()¹ para dividir (también conocido como bin) un vector numérico en cubos discretos:

x <- c(1, 2, 5, 10, 15, 20)
cut(x, breaks = c(0, 5, 10, 15, 20))
#> [1] (0,5]   (0,5]   (0,5]   (5,10]  (10,15] (15,20]
#> Levels: (0,5] (5,10] (10,15] (15,20]

Los cortes no necesitan estar espaciados uniformemente:

cut(x, breaks = c(0, 5, 10, 100))
#> [1] (0,5]    (0,5]    (0,5]    (5,10]   (10,100] (10,100]
#> Levels: (0,5] (5,10] (10,100]

Opcionalmente, puede proporcionar sus propias etiquetas, labels. Tenga en cuenta que debe haber una etiqueta, labels, menos que rupturas, breaks.

cut(x, 
  breaks = c(0, 5, 10, 15, 20), 
  labels = c("sm", "md", "lg", "xl")
)
#> [1] sm sm sm md lg xl
#> Levels: sm md lg xl

Cualquier valor fuera del rango de las rupturas se convertirá en NA:

y <- c(NA, -10, 5, 10, 30)
cut(y, breaks = c(0, 5, 10, 15, 20))
#> [1] <NA>   <NA>   (0,5]  (5,10] <NA>  
#> Levels: (0,5] (5,10] (10,15] (15,20]

Consulte la documentación para ver otros argumentos útiles como right e include.lowest, que controlan si los intervalos son [a, b) o (a, b] y si el intervalo más bajo debe ser [a, b].

13.4.7 Agregados acumulativos y rodantes

Base R proporciona cumsum(), cumprod(), cummin(), cummax() para ejecutar, o acumular, sumas, productos, mínimos y máximos. dplyr proporciona cummean() para medios acumulativos. Las sumas acumulativas tienden a ser las más importantes en la práctica:

x <- 1:10
cumsum(x)
#>  [1]  1  3  6 10 15 21 28 36 45 55

Si necesita agregados rodantes o deslizantes más complejos, pruebe el paquete slider.

13.4.8 Ejercicios

1. Explique con palabras qué hace cada línea del código utilizado para generar Figura 13.1.

2. ¿Qué funciones trigonométricas proporciona R? Adivina algunos nombres y busca la documentación. ¿Usan grados o radianes?

3. Actualmente, dep_time y sched_dep_time son convenientes de ver, pero difíciles de calcular porque en realidad no son números continuos. Puede ver el problema básico ejecutando el siguiente código: hay un intervalo entre cada hora.

   flights |> 
     filter(month == 1, day == 1) |> 
     ggplot(aes(x = sched_dep_time, y = dep_delay)) +
     geom_point()

   Conviértalos a una representación más veraz del tiempo (ya sean horas fraccionarias o minutos desde la medianoche).

4. Redondea dep_time y arr_time a los cinco minutos más cercanos.

13.5 Transformaciones generales

Las siguientes secciones describen algunas transformaciones generales que se usan a menudo con vectores numéricos, pero que se pueden aplicar a todos los demás tipos de columnas.

13.5.1 Rangos

dplyr proporciona una serie de funciones de clasificación inspiradas en SQL, pero siempre debe comenzar con dplyr::min_rank(). Utiliza el método típico para tratar los empates, p.ej., 1°, 2°, 2°, 4°.

x <- c(1, 2, 2, 3, 4, NA)
min_rank(x)
#> [1]  1  2  2  4  5 NA

Tenga en cuenta que los valores más pequeños obtienen los rangos más bajos; usa desc(x) para dar a los valores más grandes los rangos más pequeños:

min_rank(desc(x))
#> [1]  5  3  3  2  1 NA

Si min_rank() no hace lo que necesita, observe las variantes dplyr::row_number(), dplyr::dense_rank(), dplyr::percent_rank() y dplyr:: cume_dist(). Consulte la documentación para obtener más información.

df <- tibble(x = x)
df |> 
  mutate(
    row_number = row_number(x),
    dense_rank = dense_rank(x),
    percent_rank = percent_rank(x),
    cume_dist = cume_dist(x)
  )
#> # A tibble: 6 × 5
#>       x row_number dense_rank percent_rank cume_dist
#>   <dbl>      <int>      <int>        <dbl>     <dbl>
#> 1     1          1          1         0          0.2
#> 2     2          2          2         0.25       0.6
#> 3     2          3          2         0.25       0.6
#> 4     3          4          3         0.75       0.8
#> 5     4          5          4         1          1  
#> 6    NA         NA         NA        NA         NA

Puede lograr muchos de los mismos resultados eligiendo el argumento ties.method adecuado para basar el rank() de R; probablemente también querrá configurar na.last = "keep" para mantener NAs como NA.

row_number() también se puede usar sin ningún argumento dentro de un verbo dplyr. En este caso, dará el número de la fila “current”. Cuando se combina con %% o %/%, esta puede ser una herramienta útil para dividir datos en grupos de tamaño similar:

df <- tibble(id = 1:10)

df |> 
  mutate(
    row0 = row_number() - 1,
    three_groups = row0 %% 3,
    three_in_each_group = row0 %/% 3
  )
#> # A tibble: 10 × 4
#>      id  row0 three_groups three_in_each_group
#>   <int> <dbl>        <dbl>               <dbl>
#> 1     1     0            0                   0
#> 2     2     1            1                   0
#> 3     3     2            2                   0
#> 4     4     3            0                   1
#> 5     5     4            1                   1
#> 6     6     5            2                   1
#> # ℹ 4 more rows

13.5.2 Compensaciones

dplyr::lead() y dplyr::lag() le permiten referirse a los valores justo antes o justo después del valor “actual”. Devuelven un vector de la misma longitud que la entrada, rellenado con NA al principio o al final:

x <- c(2, 5, 11, 11, 19, 35)
lag(x)
#> [1] NA  2  5 11 11 19
lead(x)
#> [1]  5 11 11 19 35 NA

• x - lag(x) te da la diferencia entre el valor actual y el anterior.

  x - lag(x)
  #> [1] NA  3  6  0  8 16

• x == lag(x) le indica cuándo cambia el valor actual.

  x == lag(x)
  #> [1]    NA FALSE FALSE  TRUE FALSE FALSE

Puede adelantarse o retrasarse en más de una posición utilizando el segundo argumento, n.

13.5.3 Identificadores consecutivos

A veces desea iniciar un nuevo grupo cada vez que ocurre algún evento. Por ejemplo, cuando está mirando los datos del sitio web, es común querer dividir los eventos en sesiones, donde comienza una nueva sesión después de un intervalo de más de x minutos desde la última actividad. Por ejemplo, imagina que tienes las veces que alguien visitó un sitio web:

events <- tibble(
  time = c(0, 1, 2, 3, 5, 10, 12, 15, 17, 19, 20, 27, 28, 30)
)

Y calculó el tiempo entre cada evento y descubrió si hay una brecha lo suficientemente grande como para calificar:

events <- events |> 
  mutate(
    diff = time - lag(time, default = first(time)),
    has_gap = diff >= 5
  )
events
#> # A tibble: 14 × 3
#>    time  diff has_gap
#>   <dbl> <dbl> <lgl>  
#> 1     0     0 FALSE  
#> 2     1     1 FALSE  
#> 3     2     1 FALSE  
#> 4     3     1 FALSE  
#> 5     5     2 FALSE  
#> 6    10     5 TRUE   
#> # ℹ 8 more rows

Pero, ¿cómo pasamos de ese vector lógico a algo que podamos group_by()? cumsum(), de Sección 13.4.7, viene al rescate como brecha, es decir, has_gap es TRUE, incrementará group en uno (Sección 12.4.2):

events |> mutate(
  group = cumsum(has_gap)
)
#> # A tibble: 14 × 4
#>    time  diff has_gap group
#>   <dbl> <dbl> <lgl>   <int>
#> 1     0     0 FALSE       0
#> 2     1     1 FALSE       0
#> 3     2     1 FALSE       0
#> 4     3     1 FALSE       0
#> 5     5     2 FALSE       0
#> 6    10     5 TRUE        1
#> # ℹ 8 more rows

Otro enfoque para crear variables de agrupación es consecutive_id(), que inicia un nuevo grupo cada vez que cambia uno de sus argumentos. Por ejemplo, inspirado por esta pregunta de stackoverflow, imagine que tiene un data frame con un montón de valores repetidos:

df <- tibble(
  x = c("a", "a", "a", "b", "c", "c", "d", "e", "a", "a", "b", "b"),
  y = c(1, 2, 3, 2, 4, 1, 3, 9, 4, 8, 10, 199)
)

Si desea conservar la primera fila de cada x repetida, puede usar group_by(), consecutive_id() y slice_head():

df |> 
  group_by(id = consecutive_id(x)) |> 
  slice_head(n = 1)
#> # A tibble: 7 × 3
#> # Groups:   id [7]
#>   x         y    id
#>   <chr> <dbl> <int>
#> 1 a         1     1
#> 2 b         2     2
#> 3 c         4     3
#> 4 d         3     4
#> 5 e         9     5
#> 6 a         4     6
#> # ℹ 1 more row

13.5.4 Ejercicios

1. Encuentre los 10 vuelos más retrasados usando una función de clasificación. ¿Cómo quieres manejar los empates? Lea atentamente la documentación de min_rank().

2. ¿Qué avión (tailnum) tiene el peor récord de puntualidad?

3. ¿A qué hora del día debes volar si quieres evitar los retrasos tanto como sea posible?

4. ¿Qué hace flights |> group_by(dest) |> filter(row_number() < 4)? ¿Qué hace flights |> group_by(dest) |> filter(row_number(dep_delay) < 4)?

5. Para cada destino, calcule el total de minutos de retraso. Para cada vuelo, calcule la proporción de la demora total para su destino.

6. Los retrasos suelen tener una correlación temporal: incluso una vez que se ha resuelto el problema que causó el retraso inicial, los vuelos posteriores se retrasan para permitir que salgan los vuelos anteriores. Utilizando lag(), explore cómo se relaciona el retraso promedio de un vuelo durante una hora con el retraso promedio de la hora anterior.

   flights |> 
     mutate(hour = dep_time %/% 100) |> 
     group_by(year, month, day, hour) |> 
     summarize(
       dep_delay = mean(dep_delay, na.rm = TRUE),
       n = n(),
       .groups = "drop"
     ) |> 
     filter(n > 5)

7. Mira cada destino. ¿Puedes encontrar vuelos que sean sospechosamente rápidos (es decir, vuelos que representen un posible error de ingreso de datos)? Calcule el tiempo de aire de un vuelo en relación con el vuelo más corto a ese destino. ¿Qué vuelos se retrasaron más en el aire?

8. Encuentre todos los destinos en los que vuelan al menos dos transportistas. Utilice esos destinos para obtener una clasificación relativa de los transportistas en función de su desempeño para el mismo destino.

13.6 Resúmenes numéricos

El solo uso de los recuentos, medios y sumas que ya hemos presentado puede ayudarlo mucho, pero R proporciona muchas otras funciones de resumen útiles. Aquí hay una selección que puede resultarle útil.

13.6.1 Centrar

Hasta ahora, hemos usado principalmente mean() para resumir el centro de un vector de valores. Como hemos visto en Sección 3.6, debido a que la media es la suma dividida por el recuento, es sensible incluso a unos pocos valores inusualmente altos o bajos. Una alternativa es usar median(), que encuentra un valor que se encuentra en el “medio” del vector, es decir, el 50 % de los valores está por encima y el 50 % por debajo. Dependiendo de la forma de la distribución de la variable que le interese, la media o la mediana pueden ser una mejor medida del centro. Por ejemplo, para distribuciones simétricas generalmente informamos la media, mientras que para distribuciones asimétricas generalmente informamos la mediana.

Figura 13.2 compara la media con la mediana del retraso de salida (en minutos) para cada destino. El retraso mediano siempre es menor que el retraso medio porque los vuelos a veces salen varias horas tarde, pero nunca salen varias horas antes.

flights |>
  group_by(year, month, day) |>
  summarize(
    mean = mean(dep_delay, na.rm = TRUE),
    median = median(dep_delay, na.rm = TRUE),
    n = n(),
    .groups = "drop"
  ) |> 
  ggplot(aes(x = mean, y = median)) + 
  geom_abline(slope = 1, intercept = 0, color = "white", linewidth = 2) +
  geom_point()

Figura 13.2: Un diagrama de dispersión que muestra las diferencias de resumir el retraso de salida por día con la mediana en lugar de la media.

También puede preguntarse sobre la moda o el valor más común. Este es un resumen que solo funciona bien para casos muy simples (por eso es posible que lo hayas aprendido en la escuela secundaria), pero no funciona bien para muchos conjuntos de datos reales. Si los datos son discretos, puede haber varios valores más comunes, y si los datos son continuos, es posible que no haya un valor más común porque cada valor es ligeramente diferente. Por estas razones, la moda tiende a no ser utilizada por los estadísticos y no hay una función de moda incluida en la base R².

13.6.2 Mínimo, máximo y cuantiles

¿Qué pasa si estás interesado en lugares que no sean el centro? min() y max() le darán los valores más grandes y más pequeños. Otra herramienta poderosa es quantile(), que es una generalización de la mediana: quantile(x, 0.25) encontrará el valor de x que es mayor que el 25% de los valores, quantile(x, 0.5) es equivalente a la mediana, y quantile(x, 0.95) encontrará el valor que es mayor que el 95% de los valores.

Para los datos de flights, es posible que desee observar el cuantil del 95 % de los retrasos en lugar del máximo, ya que ignorará el 5 % de la mayoría de los vuelos retrasados, lo que puede ser bastante extremo.

flights |>
  group_by(year, month, day) |>
  summarize(
    max = max(dep_delay, na.rm = TRUE),
    q95 = quantile(dep_delay, 0.95, na.rm = TRUE),
    .groups = "drop"
  )
#> # A tibble: 365 × 5
#>    year month   day   max   q95
#>   <int> <int> <int> <dbl> <dbl>
#> 1  2013     1     1   853  70.1
#> 2  2013     1     2   379  85  
#> 3  2013     1     3   291  68  
#> 4  2013     1     4   288  60  
#> 5  2013     1     5   327  41  
#> 6  2013     1     6   202  51  
#> # ℹ 359 more rows

13.6.3 Dispersión

A veces, no está tan interesado en dónde se encuentra la mayor parte de los datos, sino en cómo se distribuyen. Dos resúmenes de uso común son la desviación estándar, sd(x), y el rango intercuartílico, IQR(). No explicaremos sd() aquí porque probablemente ya estés familiarizado con él, pero IQR() podría ser nuevo — es quantile(x, 0.75) - quantile(x, 0.25) y le da el rango que contiene el 50% medio de los datos.

Podemos usar esto para revelar una pequeña rareza en los datos de vuelos. Es de esperar que la dispersión de la distancia entre el origen y el destino sea cero, ya que los aeropuertos siempre están en el mismo lugar. Pero el siguiente código hace que parezca que un aeropuerto, EGE, podría haberse mudado.

flights |> 
  group_by(origin, dest) |> 
  summarize(
    distance_iqr = IQR(distance), 
    n = n(),
    .groups = "drop"
  ) |> 
  filter(distance_iqr > 0)
#> # A tibble: 2 × 4
#>   origin dest  distance_iqr     n
#>   <chr>  <chr>        <dbl> <int>
#> 1 EWR    EGE              1   110
#> 2 JFK    EGE              1   103

13.6.4 Distribuciones

Vale la pena recordar que todas las estadísticas de resumen descritas anteriormente son una forma de reducir la distribución a un solo número. Esto significa que son fundamentalmente reductivos, y si elige el resumen incorrecto, fácilmente puede pasar por alto diferencias importantes entre los grupos. Es por eso que siempre es una buena idea visualizar la distribución antes de comprometerse con sus estadísticas de resumen.

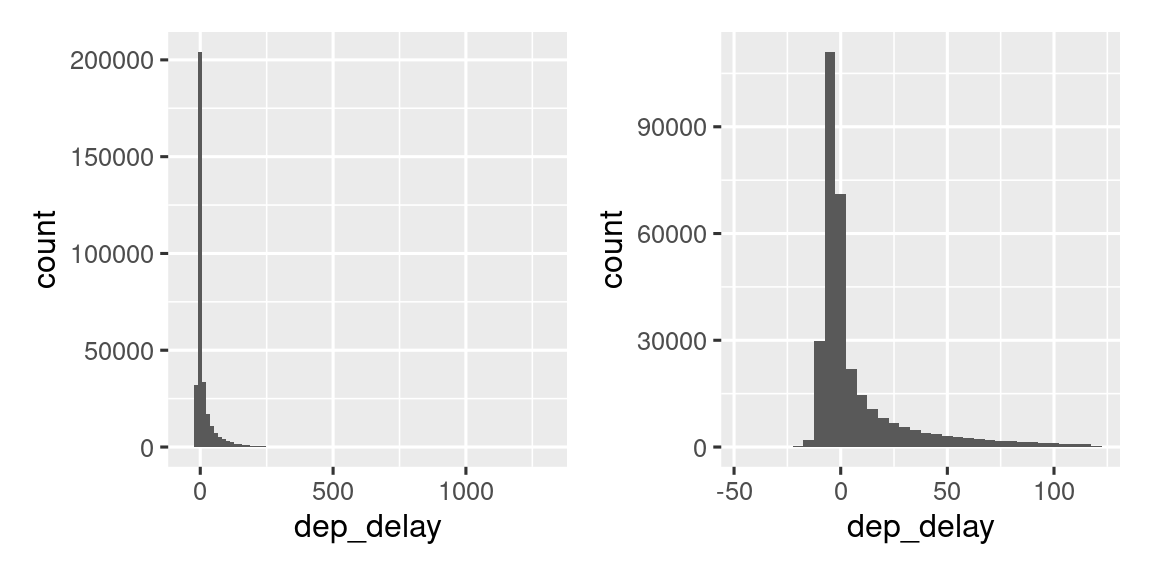
Figura 13.3 muestra la distribución general de los retrasos en las salidas. La distribución está tan sesgada que tenemos que acercarnos para ver la mayor parte de los datos. Esto sugiere que es poco probable que la media sea un buen resumen y que preferiríamos la mediana en su lugar.

Figura 13.3: (Izquierda) El histograma de los datos completos está extremadamente sesgado, lo que lo hace difícil obtener algún detalle. (Derecha) Acercamiento a retrasos de menos de dos horas hace posible ver lo que sucede con la mayor parte de la observaciones.

También es una buena idea verificar que las distribuciones de los subgrupos se parezcan al todo. En el gráfico siguiente se superponen 365 polígonos de frecuencia de dep_delay, uno para cada día. Las distribuciones parecen seguir un patrón común, lo que sugiere que está bien usar el mismo resumen para cada día.

flights |>
  filter(dep_delay < 120) |> 
  ggplot(aes(x = dep_delay, group = interaction(day, month))) + 
  geom_freqpoly(binwidth = 5, alpha = 1/5)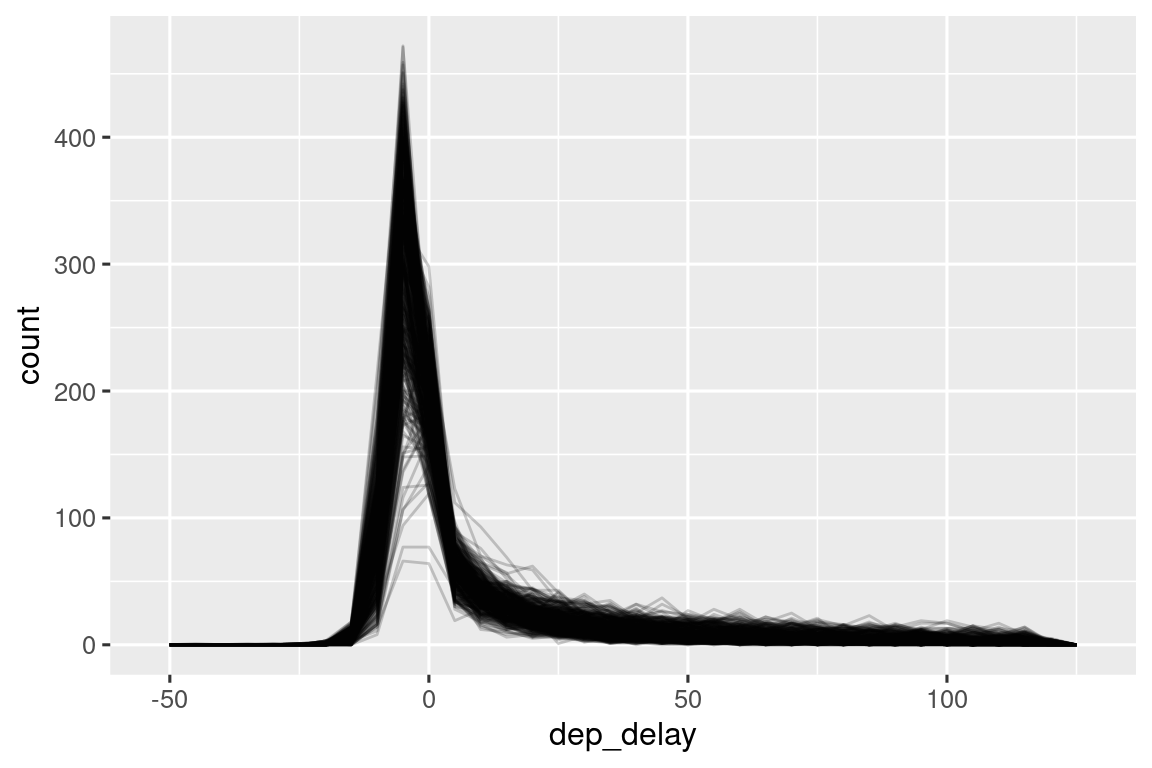

No tenga miedo de explorar sus propios resúmenes personalizados específicamente diseñados para los datos con los que está trabajando. En este caso, eso podría significar resumir por separado los vuelos que salieron temprano frente a los vuelos que salieron tarde, o dado que los valores están muy sesgados, puede intentar una transformación logarítmica. Finalmente, no olvide lo que aprendió en Sección 3.6: siempre que cree resúmenes numéricos, es una buena idea incluir el número de observaciones en cada grupo.

13.6.5 Posiciones

Hay un último tipo de resumen que es útil para los vectores numéricos, pero también funciona con cualquier otro tipo de valor: extraer un valor en una posición específica: primero(x), último(x) y nth(x, n).

Por ejemplo, podemos encontrar la primera, quinta y la última salida de cada día:

flights |> 
  group_by(year, month, day) |> 
  summarize(
    first_dep = first(dep_time, na_rm = TRUE), 
    fifth_dep = nth(dep_time, 5, na_rm = TRUE),
    last_dep = last(dep_time, na_rm = TRUE)
  )
#> `summarise()` has grouped output by 'year', 'month'. You can override using
#> the `.groups` argument.
#> # A tibble: 365 × 6
#> # Groups:   year, month [12]
#>    year month   day first_dep fifth_dep last_dep
#>   <int> <int> <int>     <int>     <int>    <int>
#> 1  2013     1     1       517       554     2356
#> 2  2013     1     2        42       535     2354
#> 3  2013     1     3        32       520     2349
#> 4  2013     1     4        25       531     2358
#> 5  2013     1     5        14       534     2357
#> 6  2013     1     6        16       555     2355
#> # ℹ 359 more rows

(NB: Debido a que las funciones dplyr usan _ para separar los componentes de la función y los nombres de los argumentos, estas funciones usan na_rm en lugar de na.rm.)

Si está familiarizado con [, al que volveremos en Sección 27.2, es posible que se pregunte si alguna vez necesitará estas funciones. Hay tres razones: el argumento default le permite proporcionar un valor predeterminado si la posición especificada no existe, el argumento order_by le permite anular localmente el orden de las filas y el argumento na_rm le permite eliminar los valores perdidos.

La extracción de valores en posiciones es complementaria al filtrado en rangos. El filtrado le brinda todas las variables, con cada observación en una fila separada:

flights |> 
  group_by(year, month, day) |> 
  mutate(r = min_rank(sched_dep_time)) |> 
  filter(r %in% c(1, max(r)))
#> # A tibble: 1,195 × 20
#> # Groups:   year, month, day [365]
#>    year month   day dep_time sched_dep_time dep_delay arr_time sched_arr_time
#>   <int> <int> <int>    <int>          <int>     <dbl>    <int>          <int>
#> 1  2013     1     1      517            515         2      830            819
#> 2  2013     1     1     2353           2359        -6      425            445
#> 3  2013     1     1     2353           2359        -6      418            442
#> 4  2013     1     1     2356           2359        -3      425            437
#> 5  2013     1     2       42           2359        43      518            442
#> 6  2013     1     2      458            500        -2      703            650
#> # ℹ 1,189 more rows
#> # ℹ 12 more variables: arr_delay <dbl>, carrier <chr>, flight <int>, …

13.6.6 Con mutate()

Como sugieren los nombres, las funciones de resumen normalmente se combinan con summarize(). Sin embargo, debido a las reglas de reciclaje que discutimos en Sección 13.4.1, también se pueden combinar de manera útil con mutate(), particularmente cuando desea realizar algún tipo de estandarización de grupo. Por ejemplo:

• x / sum(x) calcula la proporción de un total.
• (x - mean(x)) / sd(x) calcula una puntuación Z (estandarizada a media 0 y sd 1).
• (x - min(x)) / (max(x) - min(x)) se estandariza al rango [0, 1].
• x / first(x) calcula un índice basado en la primera observación.

13.6.7 Ejercicios

1. Haga una lluvia de ideas sobre al menos 5 formas diferentes de evaluar las características típicas de retraso de un grupo de vuelos. ¿Cuándo es útil mean()? ¿Cuándo es útil median()? ¿Cuándo podría querer usar otra cosa? ¿Debe utilizar el retraso de llegada o el retraso de salida? ¿Por qué querrías usar datos de aviones?

2. ¿Qué destinos muestran la mayor variación en la velocidad del aire?

3. Crea una gráfica para explorar más a fondo las aventuras de EGE. ¿Puedes encontrar alguna evidencia de que el aeropuerto cambió de ubicación? ¿Puedes encontrar otra variable que pueda explicar la diferencia?

13.7 Resumen

Ya está familiarizado con muchas herramientas para trabajar con números y, después de leer este capítulo, ahora sabe cómo usarlas en R. También aprendió un puñado de transformaciones generales útiles que se aplican comúnmente, pero no exclusivamente, a vectores numéricos como rangos y compensaciones. Finalmente, trabajó en una serie de resúmenes numéricos y discutió algunos de los desafíos estadísticos que debe considerar.

En los próximos dos capítulos, nos sumergiremos en el trabajo con cadenas con el paquete stringr. Las cadenas son un gran tema, por lo que tienen dos capítulos, uno sobre los fundamentos de las cadenas y otro sobre las expresiones regulares.

---

1. ggplot2 proporciona algunos ayudantes para casos comunes en cut_interval(), cut_number() y cut_width(). ggplot2 es un lugar ciertamente extraño para que vivan estas funciones, pero son útiles como parte del cálculo del histograma y se escribieron antes de que existieran otras partes del tidyverse.

2. ¡La función mode() hace algo muy diferente!