15  Sistemas coordinados

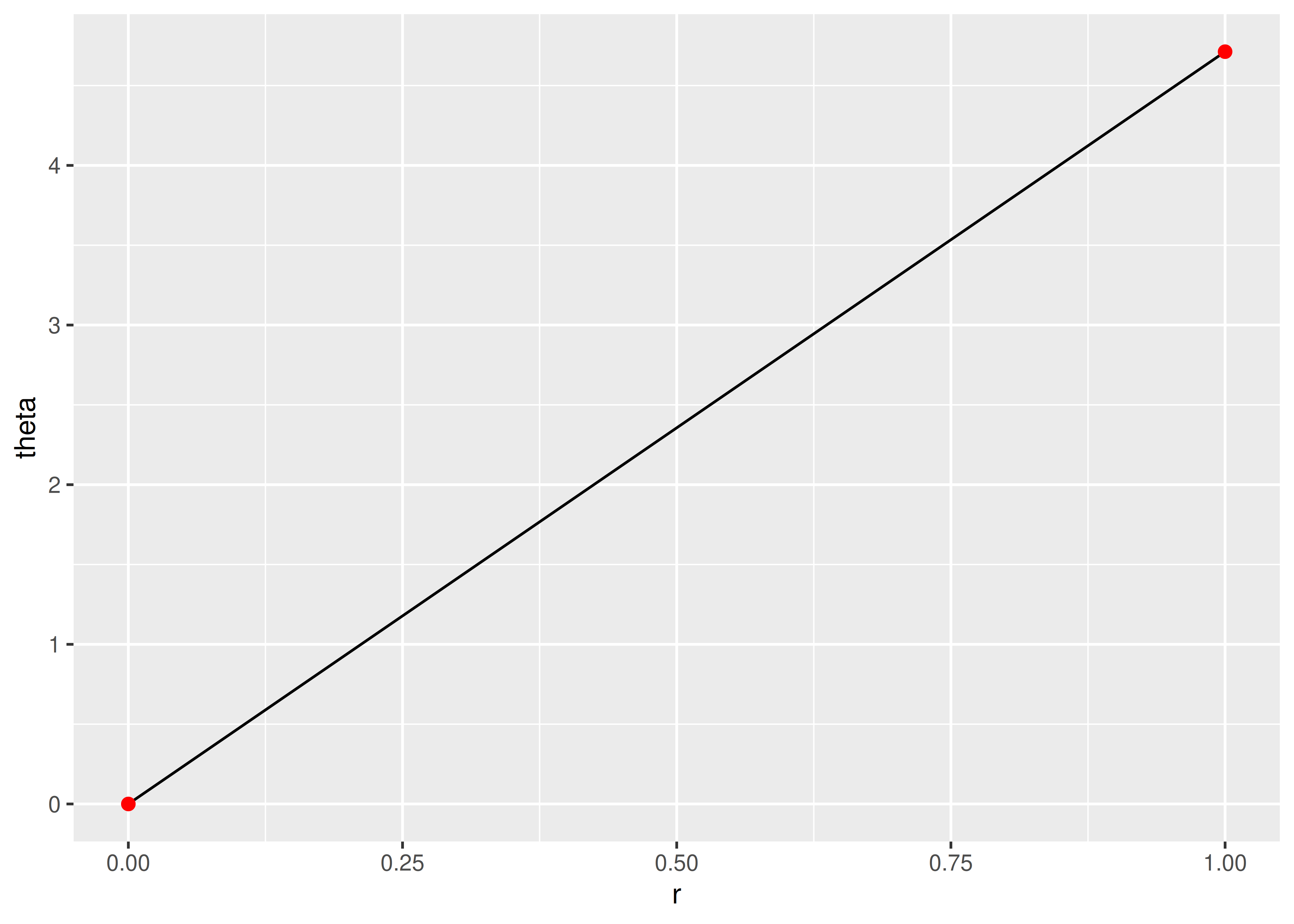
You are reading the work-in-progress third edition of the ggplot2 book. This chapter is currently a dumping ground for ideas, and we don’t recommend reading it.

Los sistemas de coordenadas tienen dos funciones principales:

Hay dos tipos de sistemas de coordenadas. Los sistemas de coordenadas lineales preservan la forma de las geoms:

Por otro lado, los sistemas de coordenadas no lineales pueden cambiar las formas: una línea recta puede dejar de ser recta. Es posible que la distancia más cercana entre dos puntos ya no sea una línea recta.

Cada sistema de coordenadas se describe con más detalle a continuación.

15.1 Sistemas de coordenadas lineales

Hay tres sistemas de coordenadas lineales: coord_cartesian(), coord_flip(), coord_fixed().

15.1.1 Acercándose a una gráfica con coord_cartesian()

coord_cartesian() tiene argumentos xlim y ylim. Si recuerda el capítulo de las escalas, se preguntará por qué las necesitamos. ¿El argumento de los límites de la balanza no nos permite ya controlar lo que aparece en la gráfica? La diferencia clave es cómo funcionan los límites: al establecer límites de escala, cualquier dato fuera de los límites se desecha; pero al establecer los límites del sistema de coordenadas, todavía usamos todos los datos, pero solo mostramos una pequeña región del gráfico. Establecer los límites del sistema de coordenadas es como mirar el gráfico con una lupa. 

base <- ggplot(mpg, aes(displ, hwy)) + 
  geom_point() + 
  geom_smooth()

# Conjunto de datos completo
base
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'
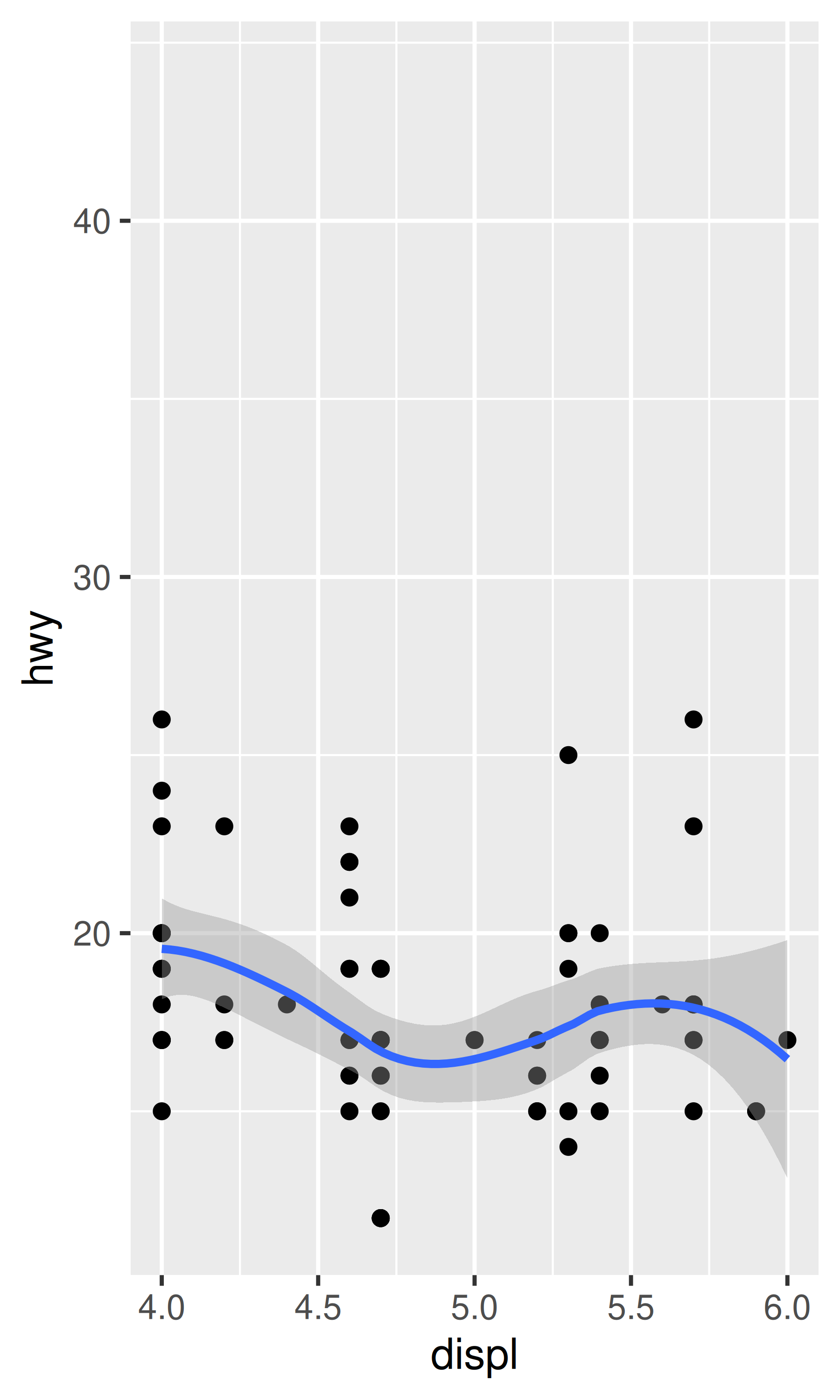
# Escalar a 4-6 descarta datos fuera de ese rango
base + scale_x_continuous(limits = c(4, 6))
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'
#> Warning: Removed 153 rows containing non-finite outside the scale range
#> (`stat_smooth()`).
#> Warning: Removed 153 rows containing missing values or values outside the scale range
#> (`geom_point()`).
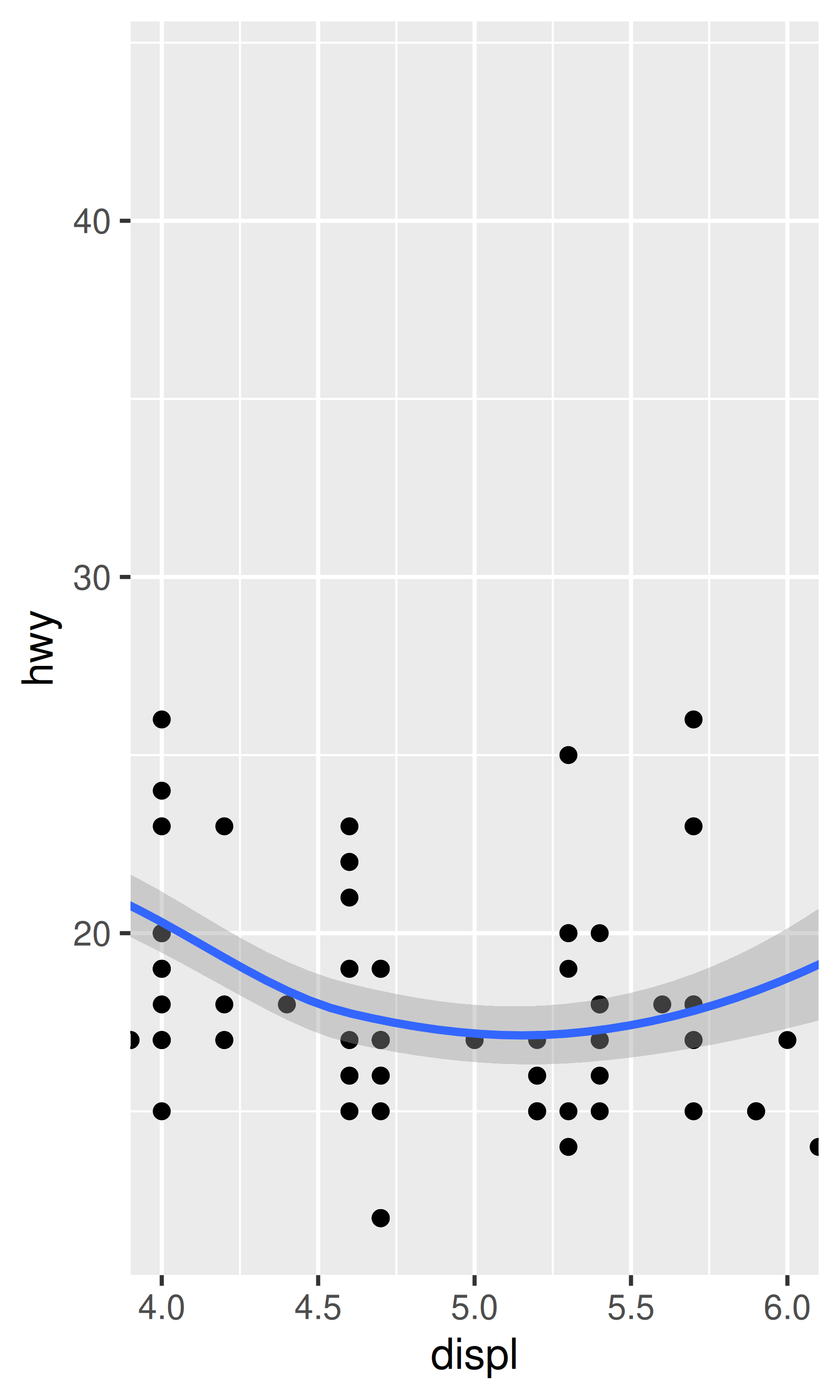
# Hacer zoom a 4--6 mantiene todos los datos pero solo muestra algunos de ellos
base + coord_cartesian(xlim = c(4, 6))
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'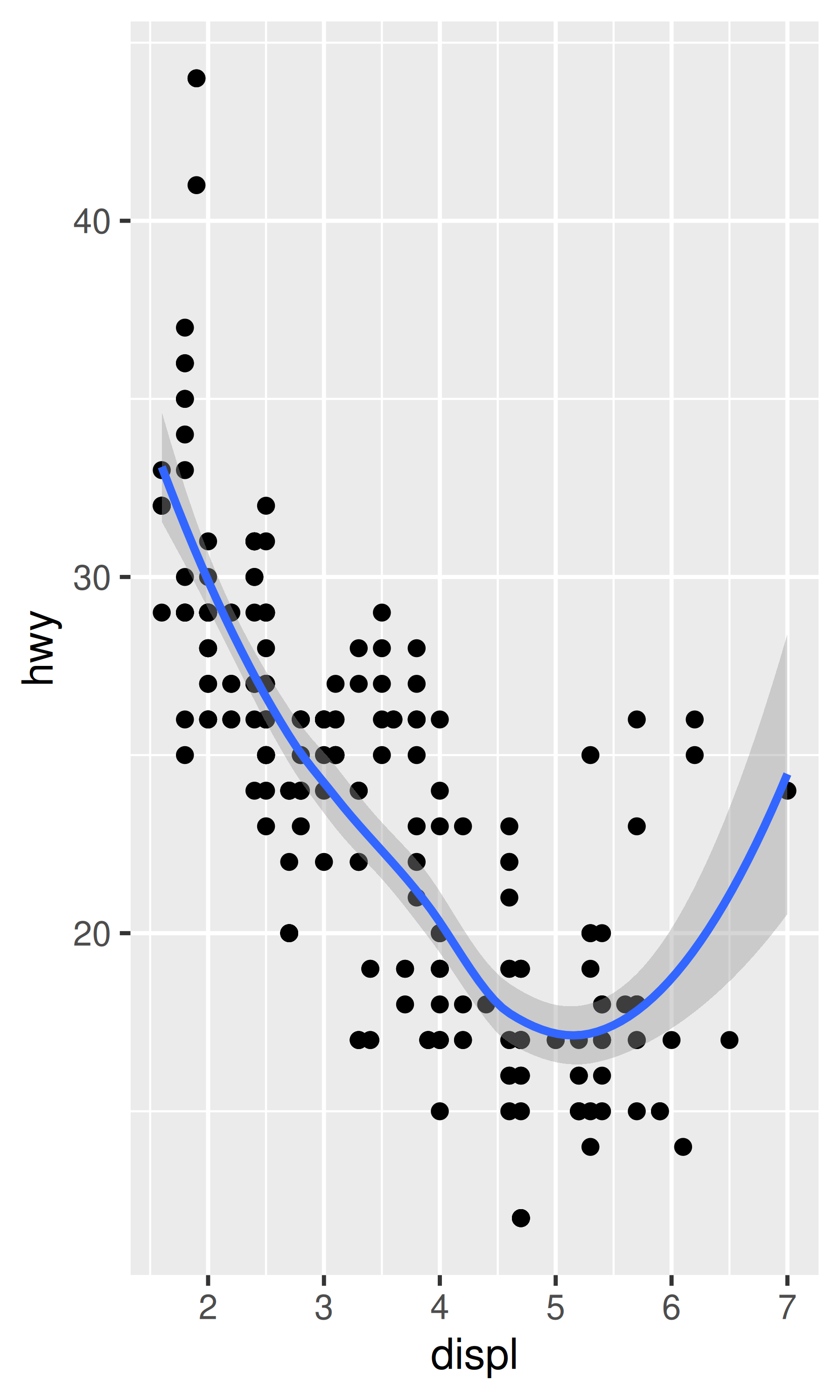

15.1.2 Voltear los ejes con coord_flip()

La mayoría de las estadísticas y geoms asumen que usted está interesado en los valores de y condicionados a los valores de x (por ejemplo, suave, resumen, diagrama de caja, línea): en la mayoría de los modelos estadísticos, se supone que los valores de x se miden sin errores. Si está interesado en x condicional a y (o simplemente desea rotar el gráfico 90 grados), puede usar coord_flip() para intercambiar los ejes x e y. Compare esto con simplemente intercambiar las variables asignadas a x e y: 

ggplot(mpg, aes(displ, cty)) + 
  geom_point() + 
  geom_smooth()
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'
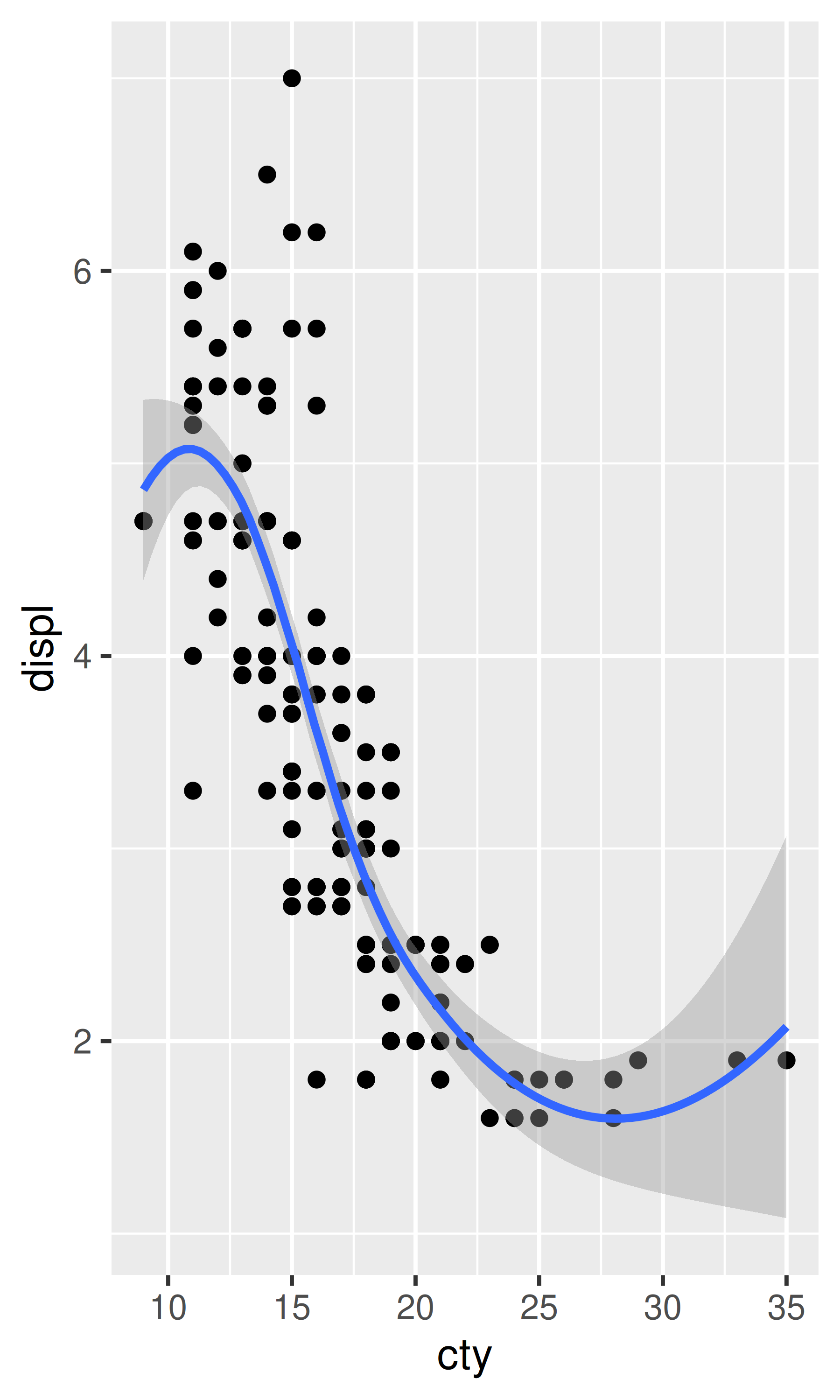
# El intercambio de cty y displ gira la gráfica 90 grados, pero la fluidez
# se ajusta a los datos rotados.
ggplot(mpg, aes(cty, displ)) + 
  geom_point() + 
  geom_smooth()
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'
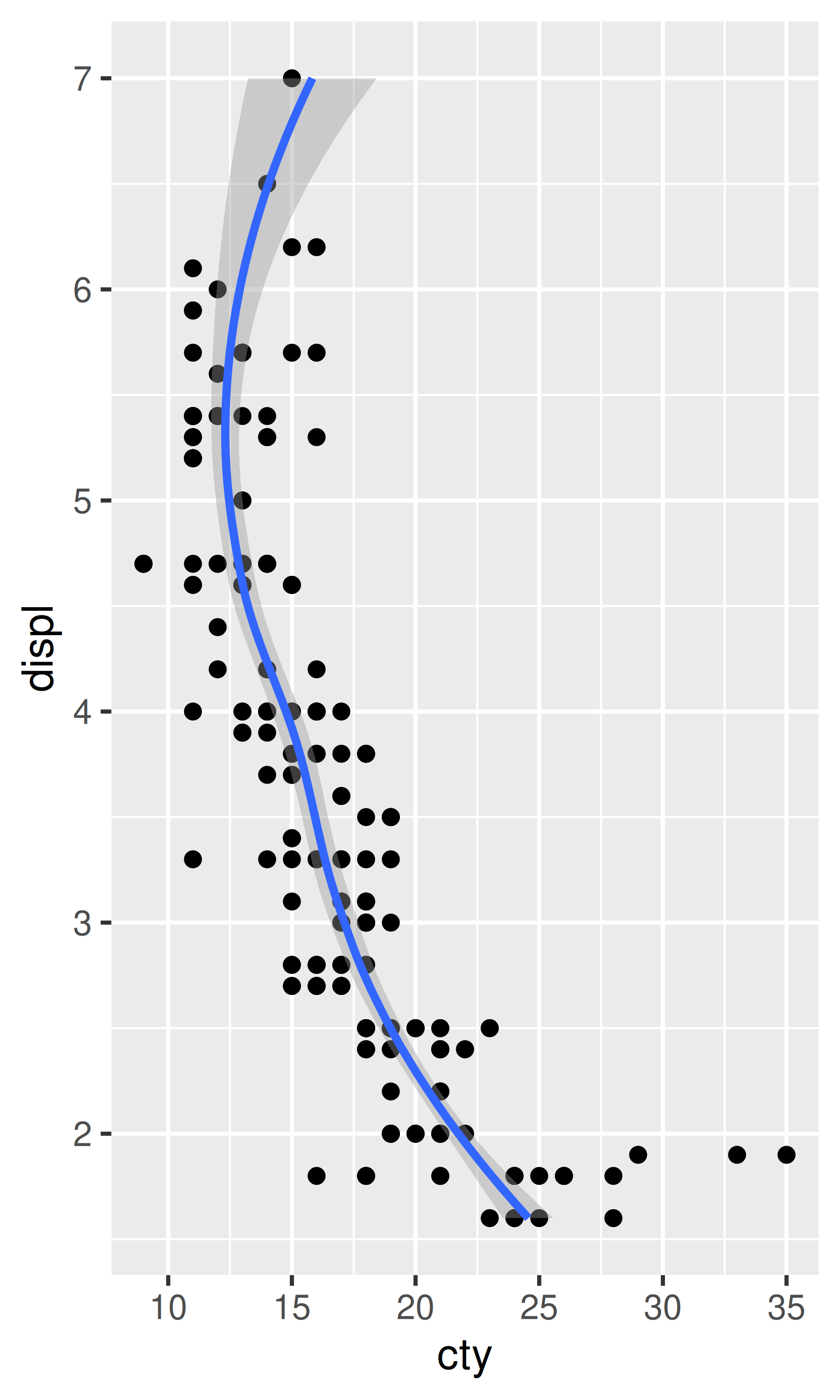
# coord_flip() ajusta la suavidad a los datos originales y luego gira
# la salida
ggplot(mpg, aes(displ, cty)) + 
  geom_point() + 
  geom_smooth() + 
  coord_flip()
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'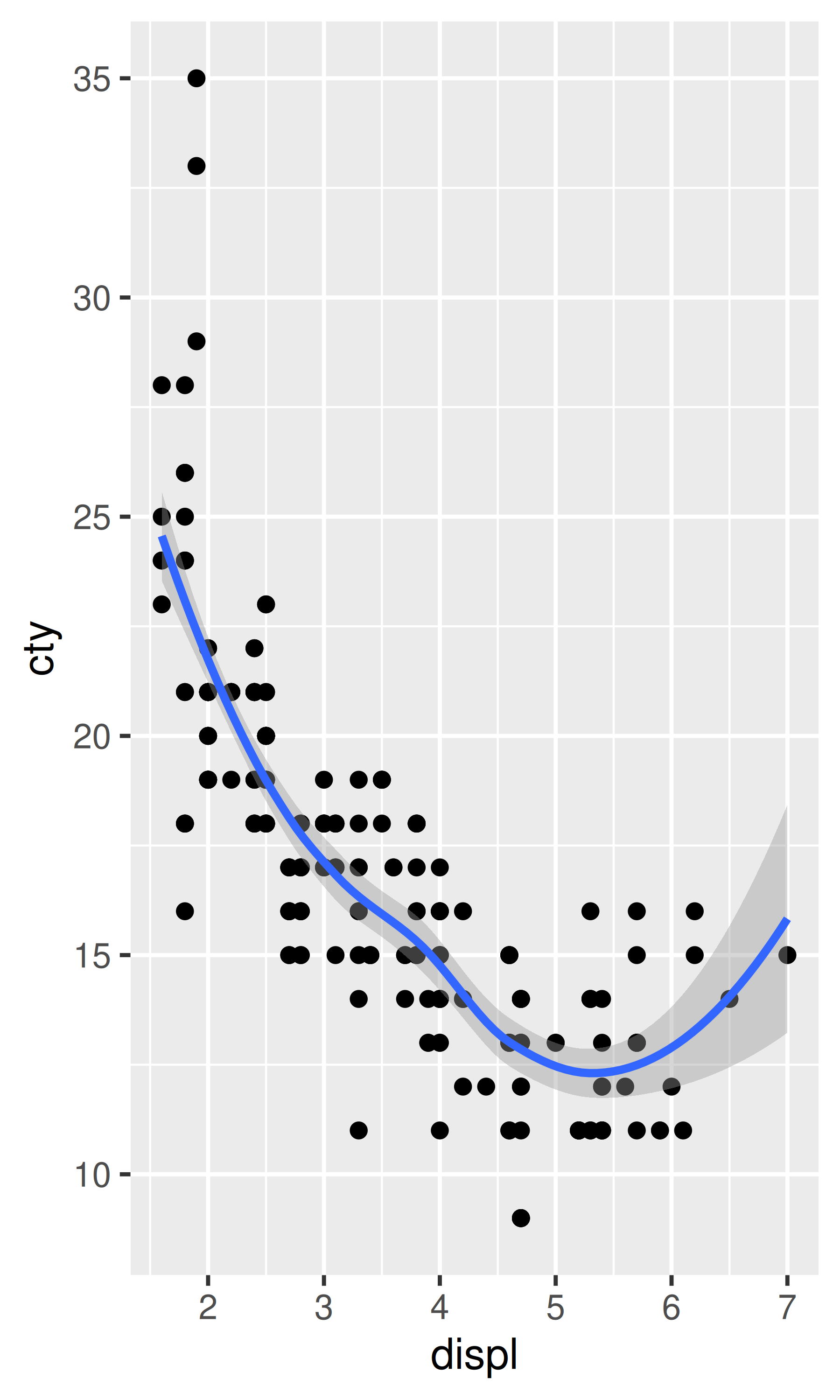

15.1.3 Escalas iguales con coord_fixed()

coord_fixed() Fija la relación de longitud en los ejes x e y. El ratio predeterminado garantiza que los ejes x e y tengan escalas iguales: es decir, 1 cm a lo largo del eje x representa el mismo rango de datos que 1 cm a lo largo del eje y. La relación de aspecto también se establecerá para garantizar que el mapeo se mantenga independientemente de la forma del dispositivo de salida. Consulte la documentación de coord_fixed() para obtener más detalles.

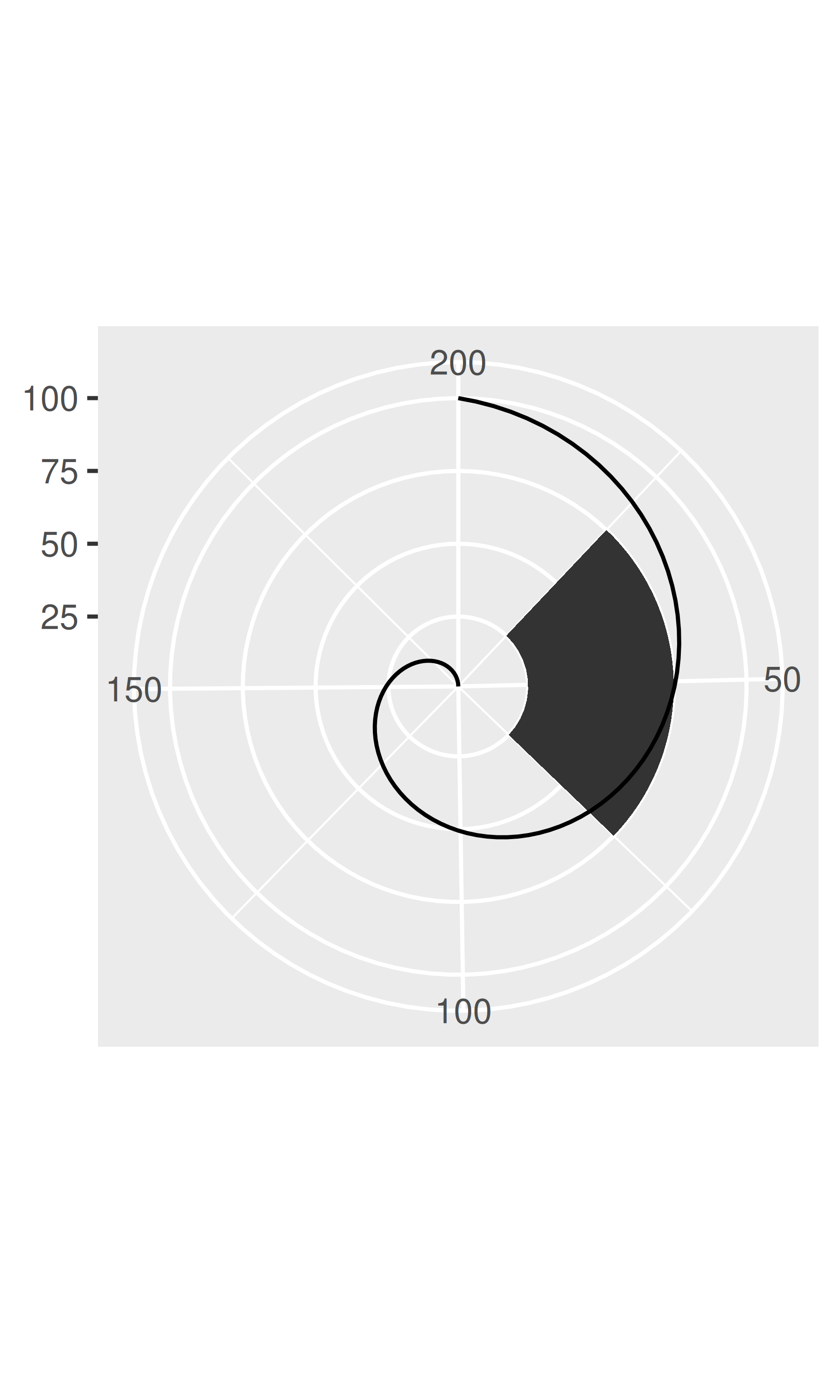
15.2 Sistemas de coordenadas no lineales

A diferencia de las coordenadas lineales, las coordenadas no lineales pueden cambiar la forma de las geoms. Por ejemplo, en coordenadas polares un rectángulo se convierte en un arco; En una proyección cartográfica, el camino más corto entre dos puntos no es necesariamente una línea recta. El siguiente código muestra cómo se representan una línea y un rectángulo en algunos sistemas de coordenadas diferentes. 

rect <- data.frame(x = 50, y = 50)
line <- data.frame(x = c(1, 200), y = c(100, 1))
base <- ggplot(mapping = aes(x, y)) + 
  geom_tile(data = rect, aes(width = 50, height = 50)) + 
  geom_line(data = line) + 
  xlab(NULL) + ylab(NULL)
base
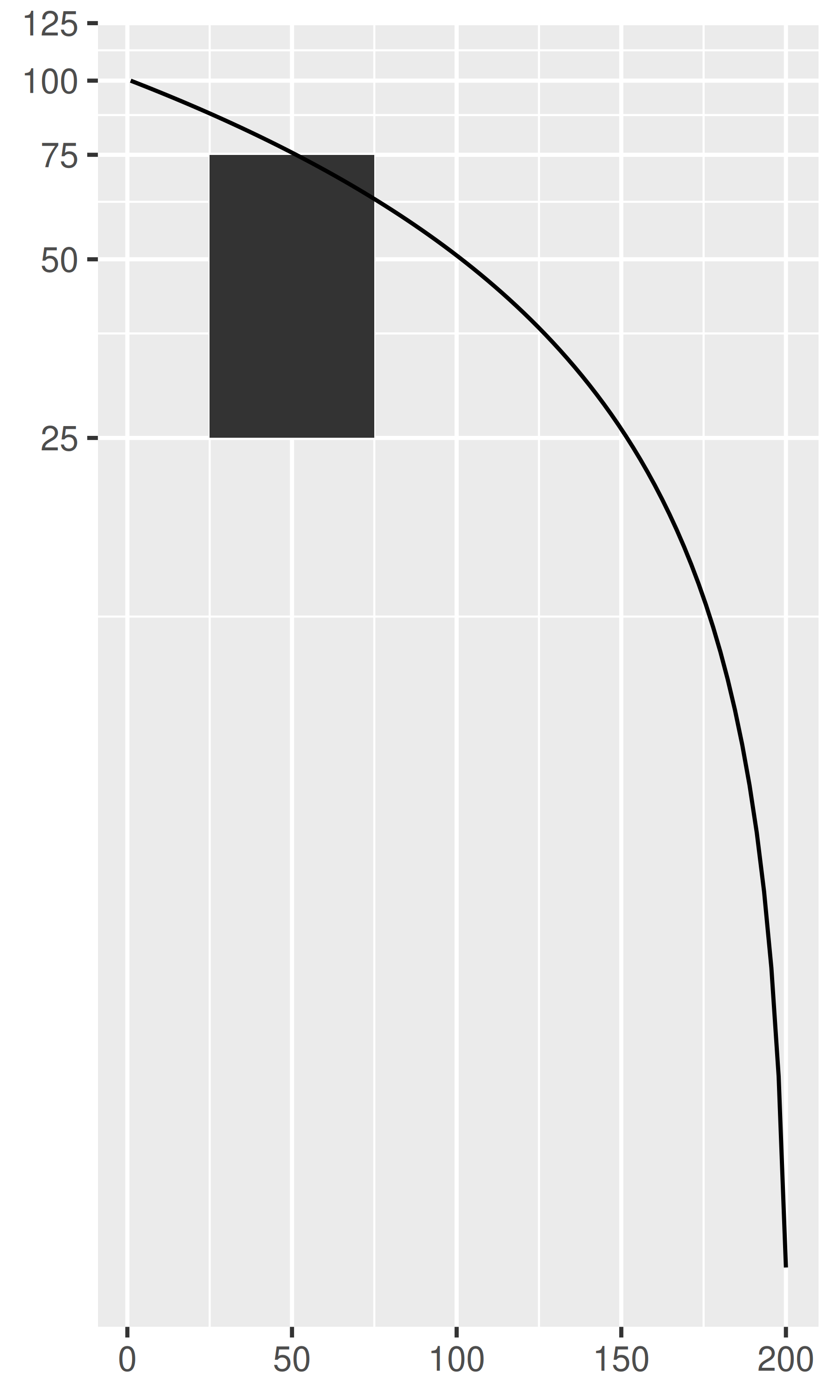
base + coord_polar("x")
base + coord_polar("y")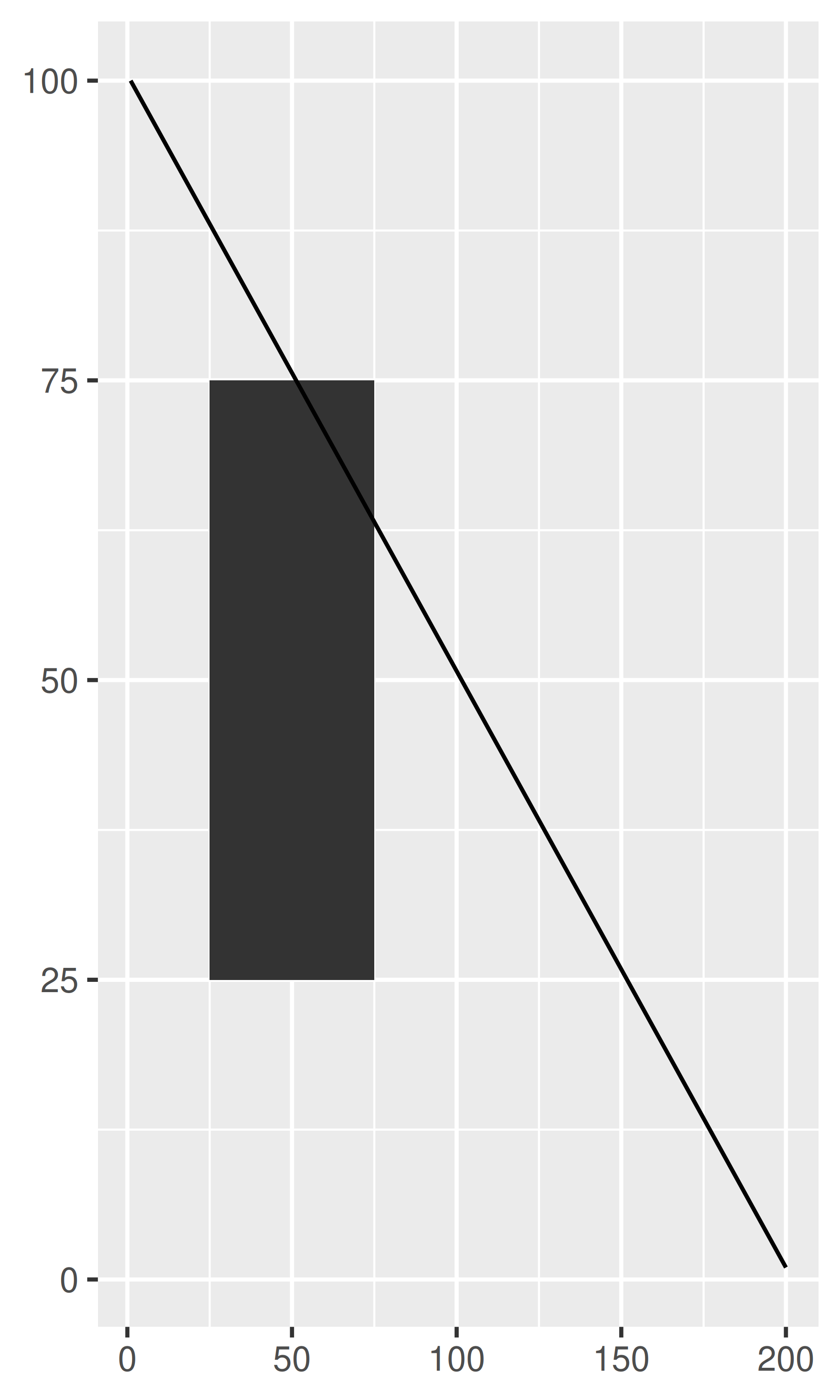

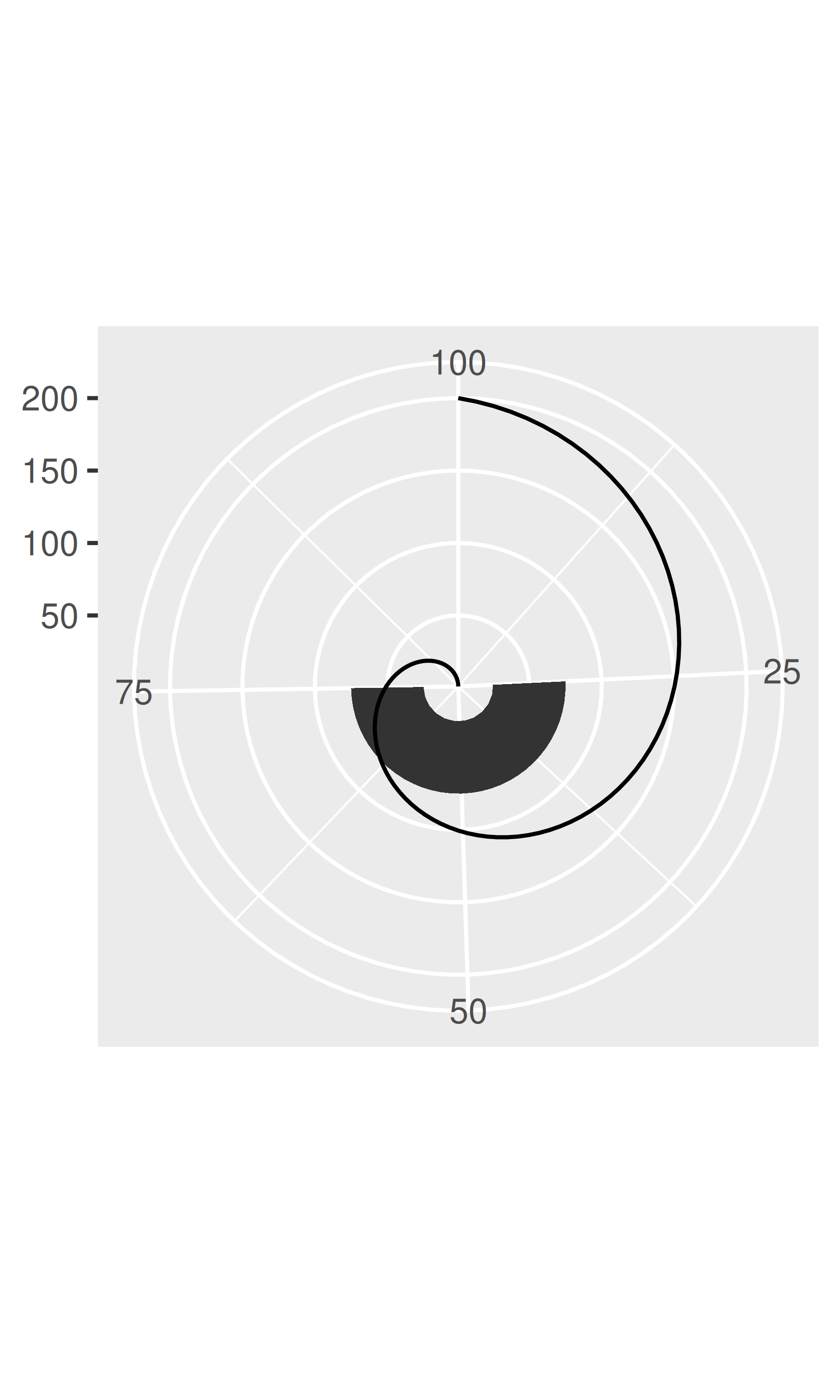
base + coord_flip()
base + coord_trans(y = "log10")
base + coord_fixed()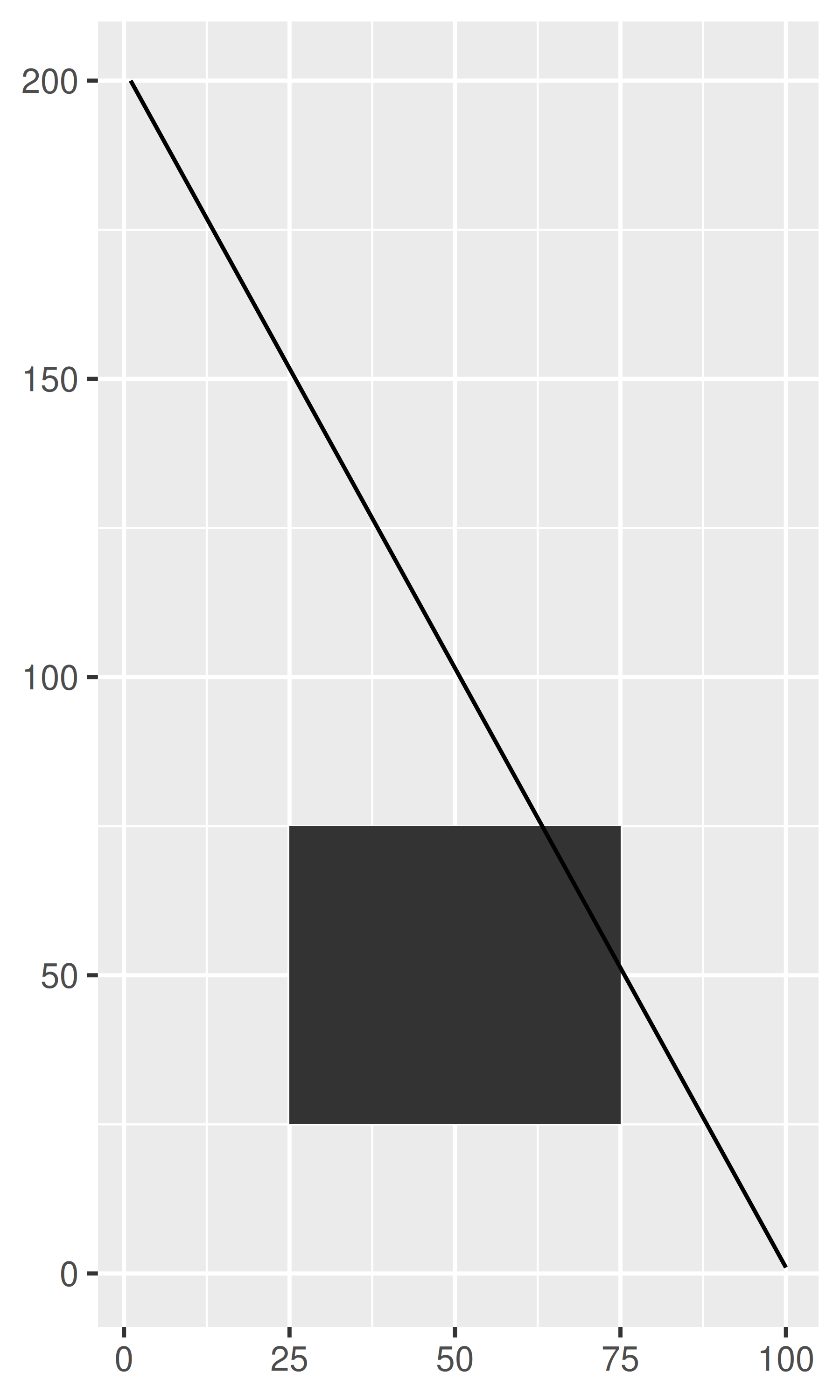

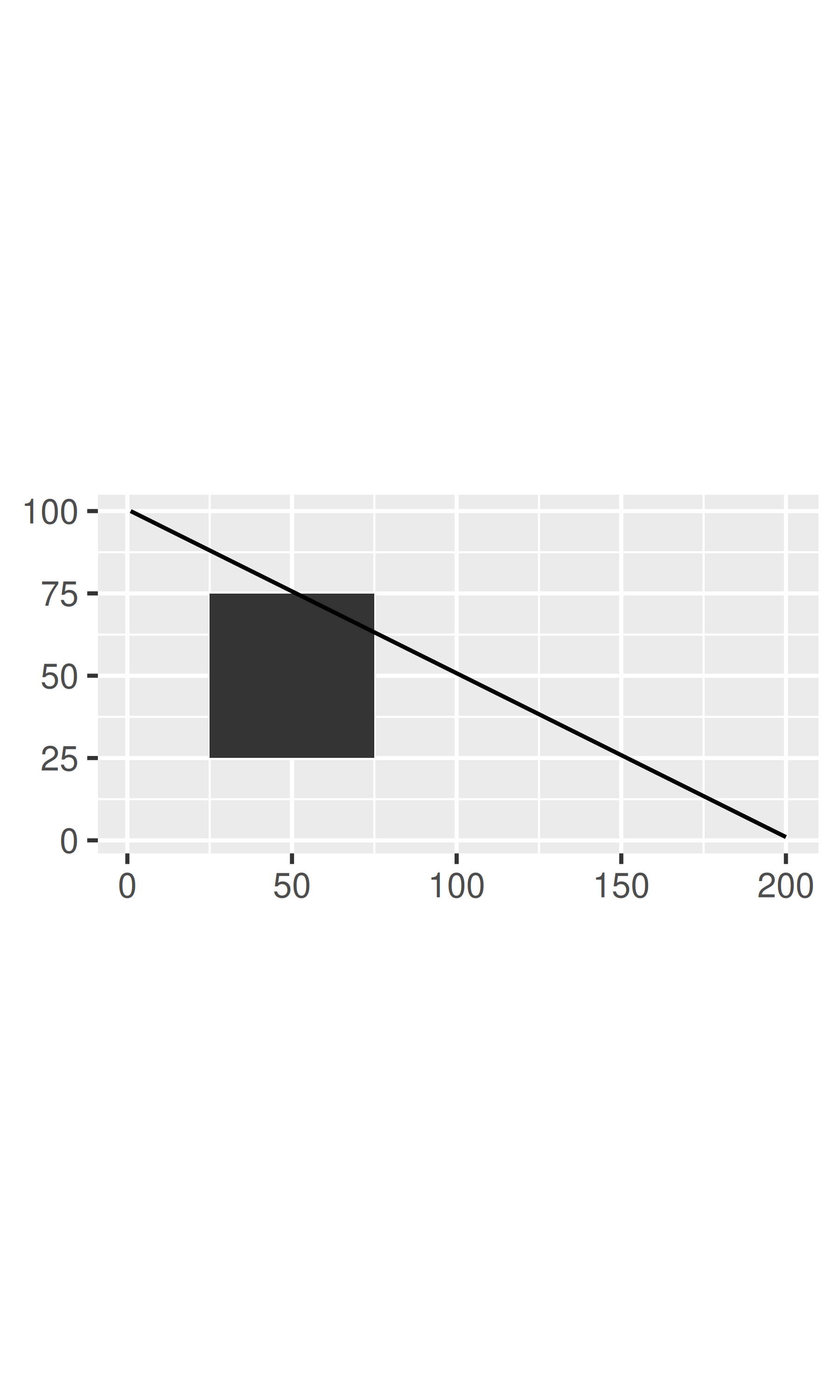
La transformación se produce en dos pasos. En primer lugar, la parametrización de cada geom se cambia para que se base puramente en la ubicación, en lugar de en la ubicación y las dimensiones. Por ejemplo, una barra se puede representar como una posición x (una ubicación), una altura y un ancho (dos dimensiones). Interpretar la altura y el ancho en un sistema de coordenadas no cartesiano es difícil porque es posible que un rectángulo ya no tenga una altura y un ancho constantes, por lo que lo convertimos a una representación puramente basada en la ubicación, un polígono definido por las cuatro esquinas. Esto convierte efectivamente todas las geoms en una combinación de puntos, líneas y polígonos.

Una vez que todas las geoms tengan una representación basada en la ubicación, el siguiente paso es transformar cada ubicación en el nuevo sistema de coordenadas. Es fácil transformar puntos, porque un punto sigue siendo un punto sin importar en qué sistema de coordenadas se encuentre. Las líneas y los polígonos son más difíciles, porque es posible que una línea recta ya no lo sea en el nuevo sistema de coordenadas. Para que el problema sea manejable, asumimos que todas las transformaciones de coordenadas son suaves, en el sentido de que todas las líneas muy cortas seguirán siendo líneas rectas muy cortas en el nuevo sistema de coordenadas. Con esta suposición en la mano, podemos transformar líneas y polígonos dividiéndolos en muchos segmentos de línea pequeños y transformando cada segmento. Este proceso se llama masticar y se ilustra a continuación:

  1. Empezamos con una línea parametrizada por sus dos extremos:

    df <- data.frame(r = c(0, 1), theta = c(0, 3 / 2 * pi))
ggplot(df, aes(r, theta)) + 
  geom_line() + 
  geom_point(size = 2, colour = "red")

  2. Lo dividimos en varios segmentos de línea, cada uno con dos puntos finales.

    interp <- function(rng, n) {
  seq(rng[1], rng[2], length = n)
}
munched <- data.frame(
  r = interp(df$r, 15),
  theta = interp(df$theta, 15)
)

ggplot(munched, aes(r, theta)) + 
  geom_line() + 
  geom_point(size = 2, colour = "red")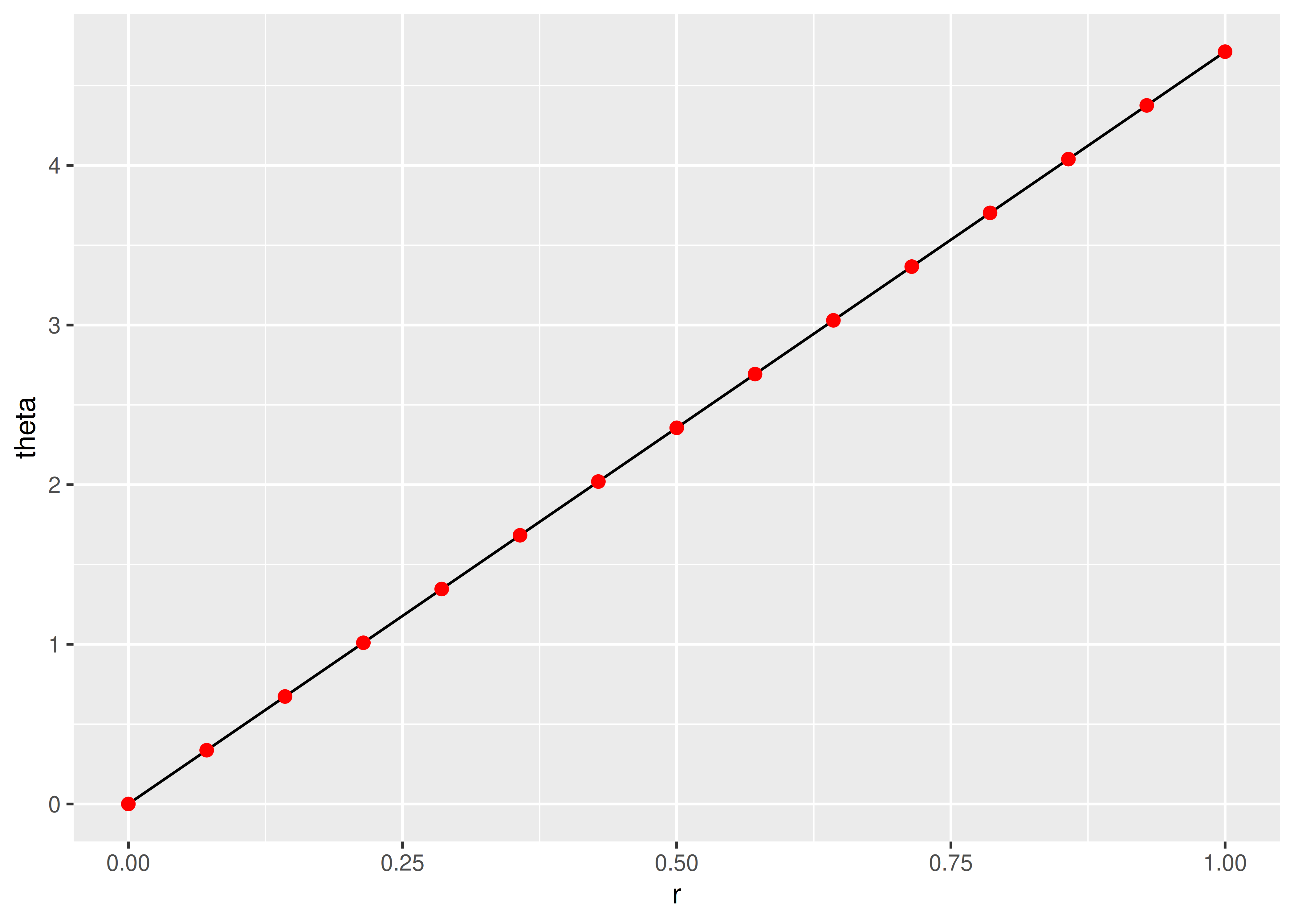

  3. Transformamos las ubicaciones de cada pieza:

    transformed <- transform(munched,
  x = r * sin(theta),
  y = r * cos(theta)
)

ggplot(transformed, aes(x, y)) + 
  geom_path() + 
  geom_point(size = 2, colour = "red") + 
  coord_fixed()

Internamente, ggplot2 usa muchos más segmentos para que el resultado parezca fluido.

15.2.1 Transformaciones con coord_trans()

Al igual que los límites, también podemos transformar los datos en dos lugares: a nivel de escala o a nivel del sistema de coordenadas. coord_trans() tiene argumentos x e y que deberían ser cadenas que nombren el transformador o los objetos del transformador (ver Capítulo 10). La transformación a nivel de escala ocurre antes de que se calculen las estadísticas y no cambia la forma de la geom. La transformación a nivel del sistema de coordenadas ocurre después de que se han calculado las estadísticas y afecta la forma de la geom. Usar ambos juntos nos permite modelar los datos en una escala transformada y luego transformarlos para su interpretación: un patrón común en el análisis. 

# El modelo lineal en la escala original no se ajusta bien
base <- ggplot(diamonds, aes(carat, price)) + 
  stat_bin2d() + 
  geom_smooth(method = "lm") + 
  xlab(NULL) + 
  ylab(NULL) + 
  theme(legend.position = "none")
base

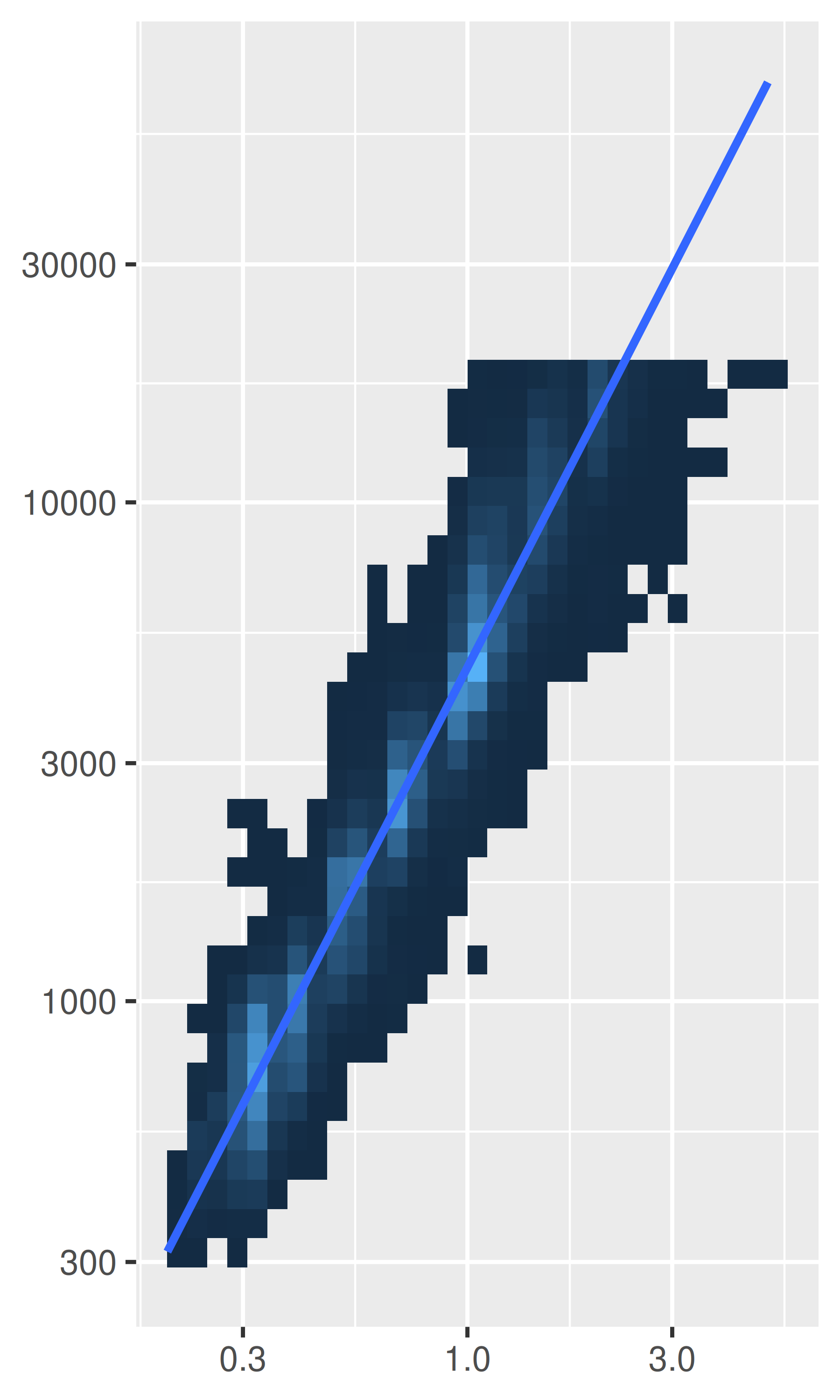
# Mejor ajuste en escala logarítmica, pero más difícil de interpretar
base +
  scale_x_log10() + 
  scale_y_log10()

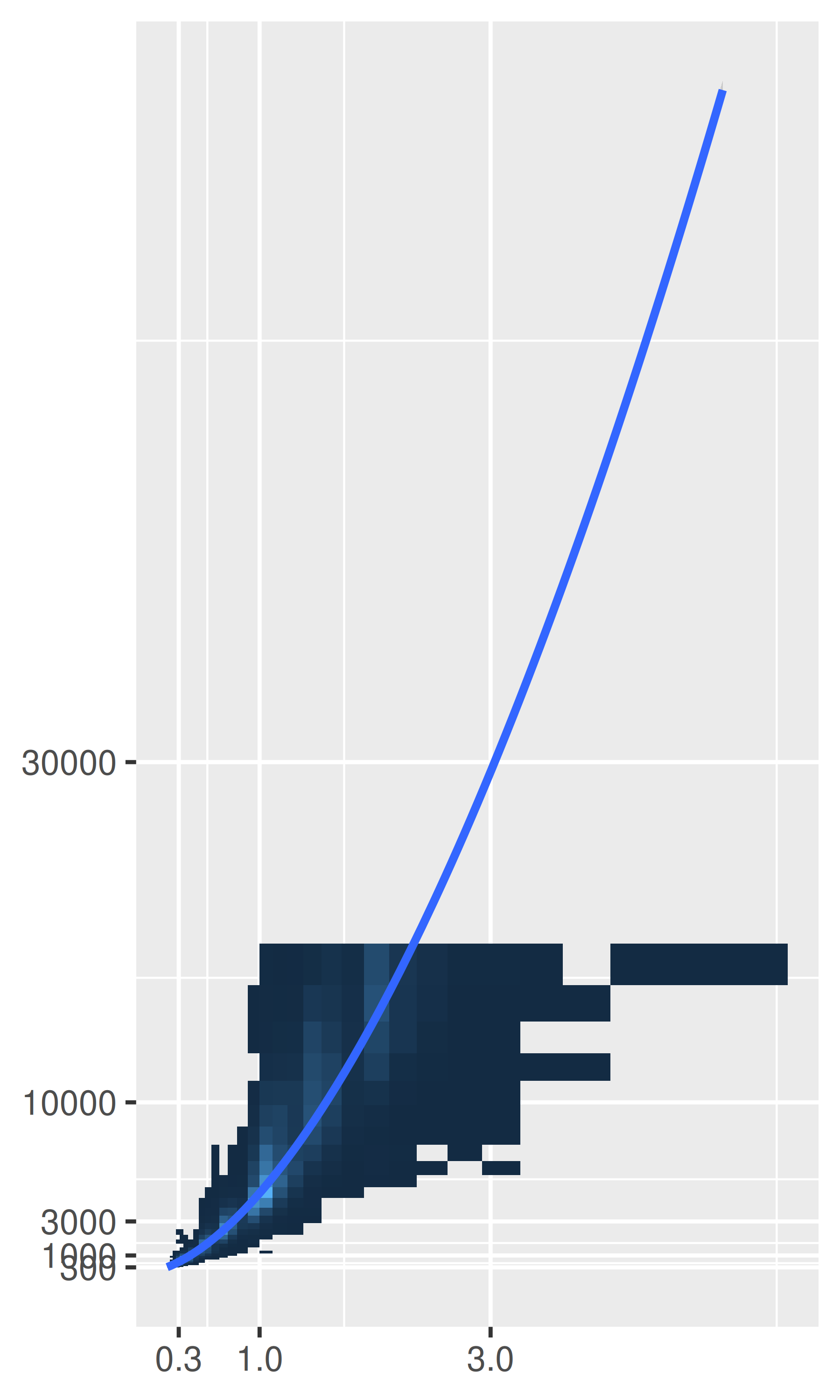
# Ajustar a escala logarítmica y luego volver a transformar al original.
# Destaca la falta de diamantes caros con grandes quilates
pow10 <- scales::exp_trans(10)
base +
  scale_x_log10() + 
  scale_y_log10() + 
  coord_trans(x = pow10, y = pow10)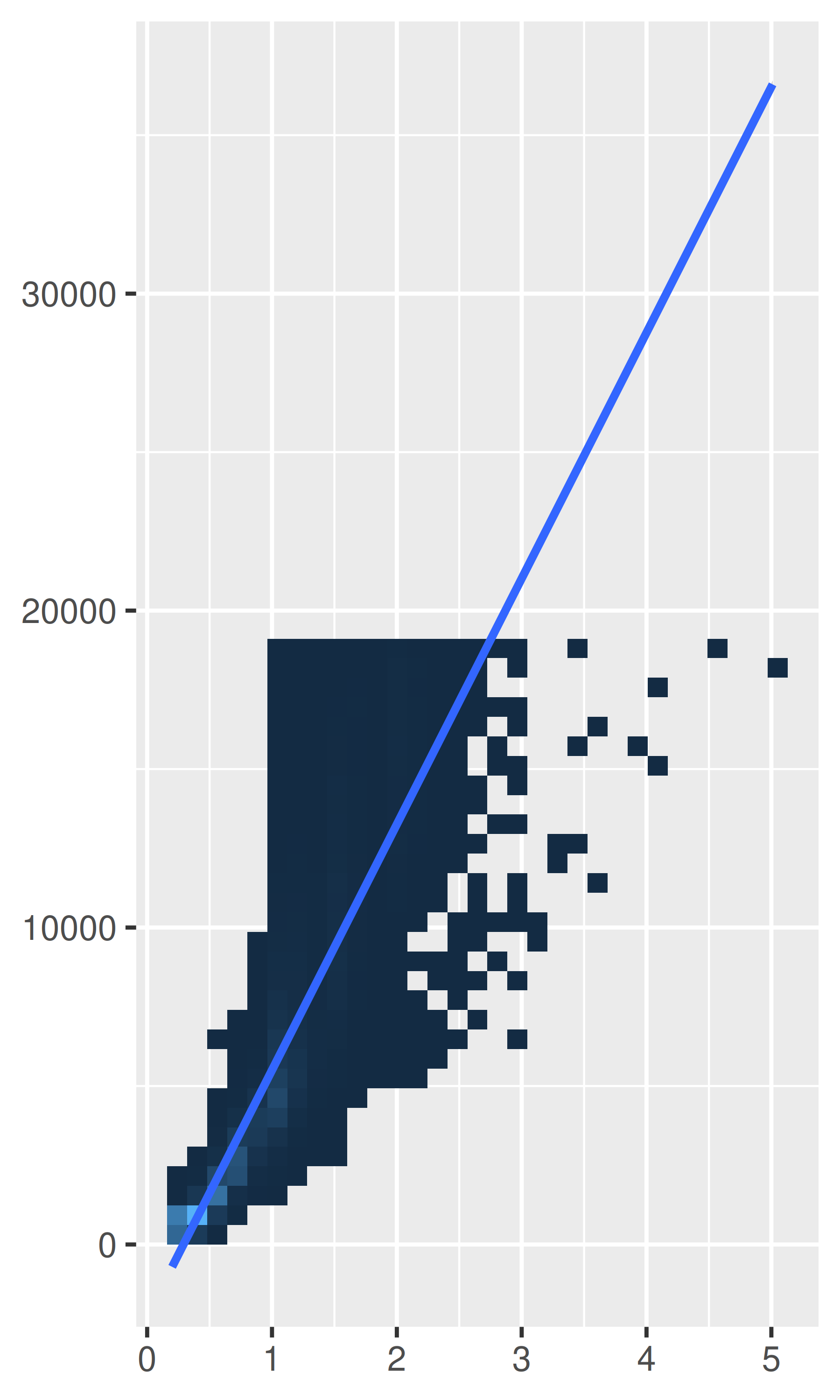

15.2.2 Coordenadas polares con coord_polar()

El uso de coordenadas polares da lugar a gráficos circulares y rosas de los vientos (de geomas de barras) y gráficos de radar (de geomas de líneas). Las coordenadas polares se utilizan a menudo para datos circulares, particularmente tiempo o dirección, pero las propiedades de percepción no son buenas porque el ángulo es más difícil de percibir para radios pequeños que para radios grandes. El argumento theta determina qué variable de posición se asigna al ángulo (por defecto, x) y cuál al radio.

El siguiente código muestra cómo podemos convertir una barra en un gráfico circular o en un gráfico de diana cambiando el sistema de coordenadas. La documentación incluye otros ejemplos. 

base <- ggplot(mtcars, aes(factor(1), fill = factor(cyl))) +
  geom_bar(width = 1) + 
  theme(legend.position = "none") + 
  scale_x_discrete(NULL, expand = c(0, 0)) +
  scale_y_continuous(NULL, expand = c(0, 0))

# diagrama de barras apiladas
base

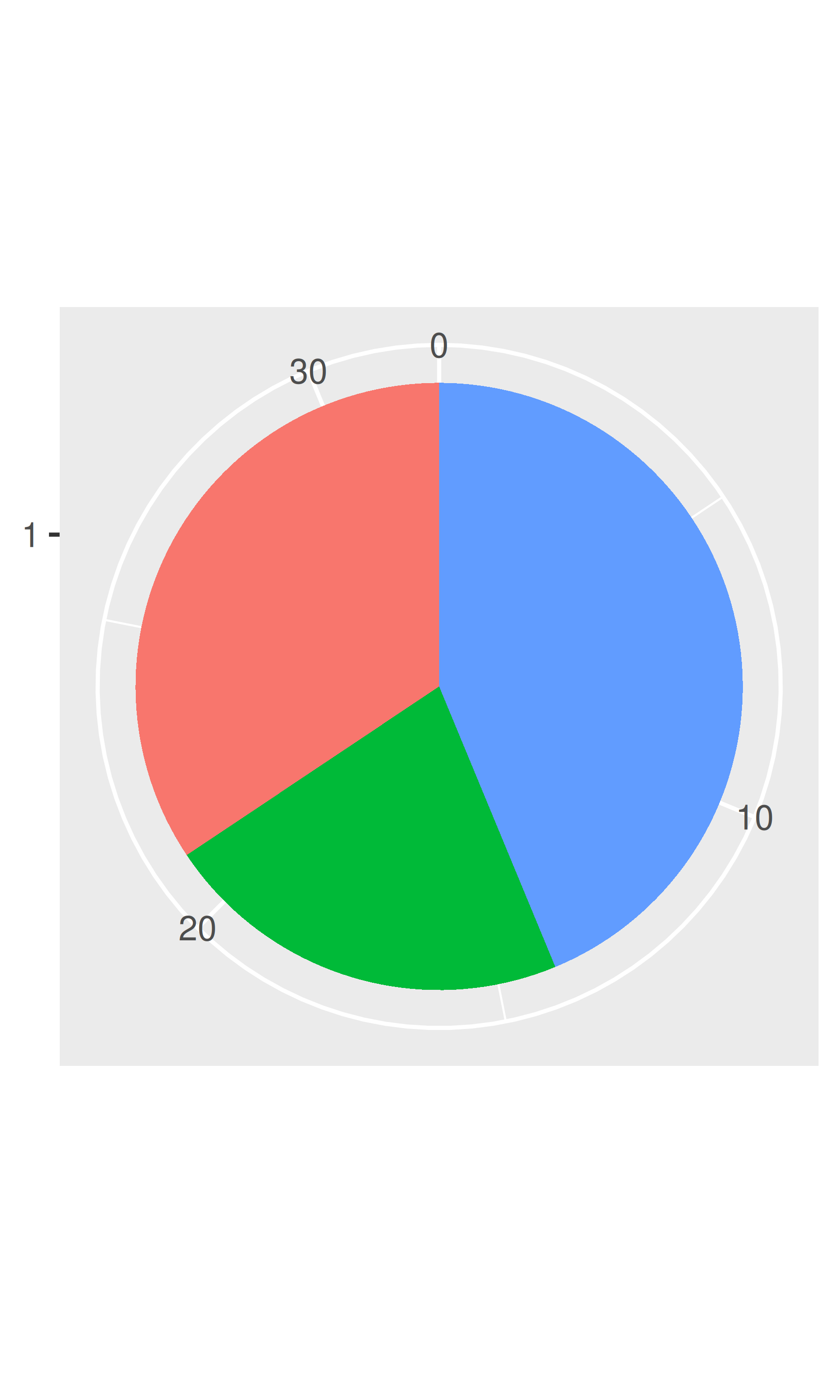
# Gráfico circular
base + coord_polar(theta = "y")

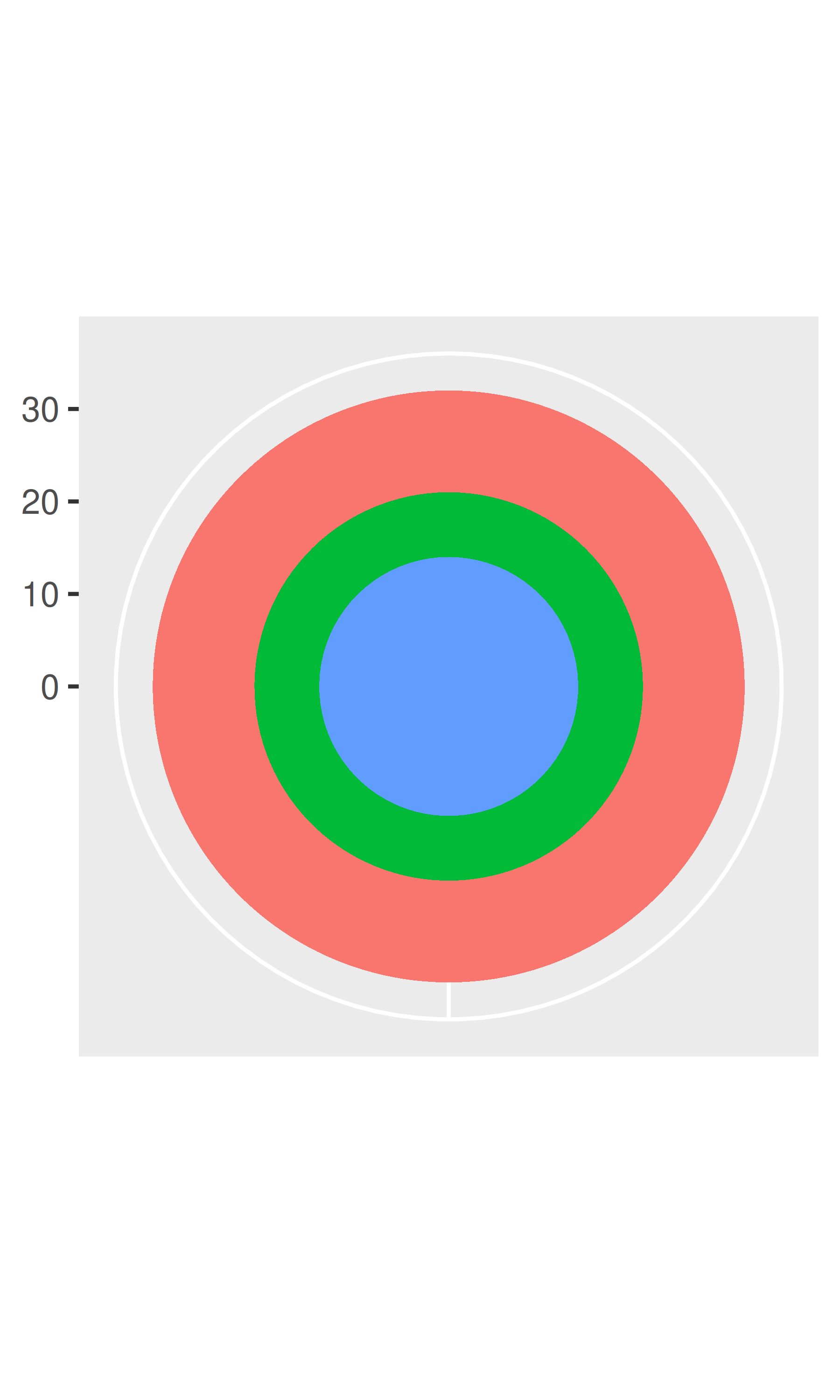
# El gráfico de diana
base + coord_polar()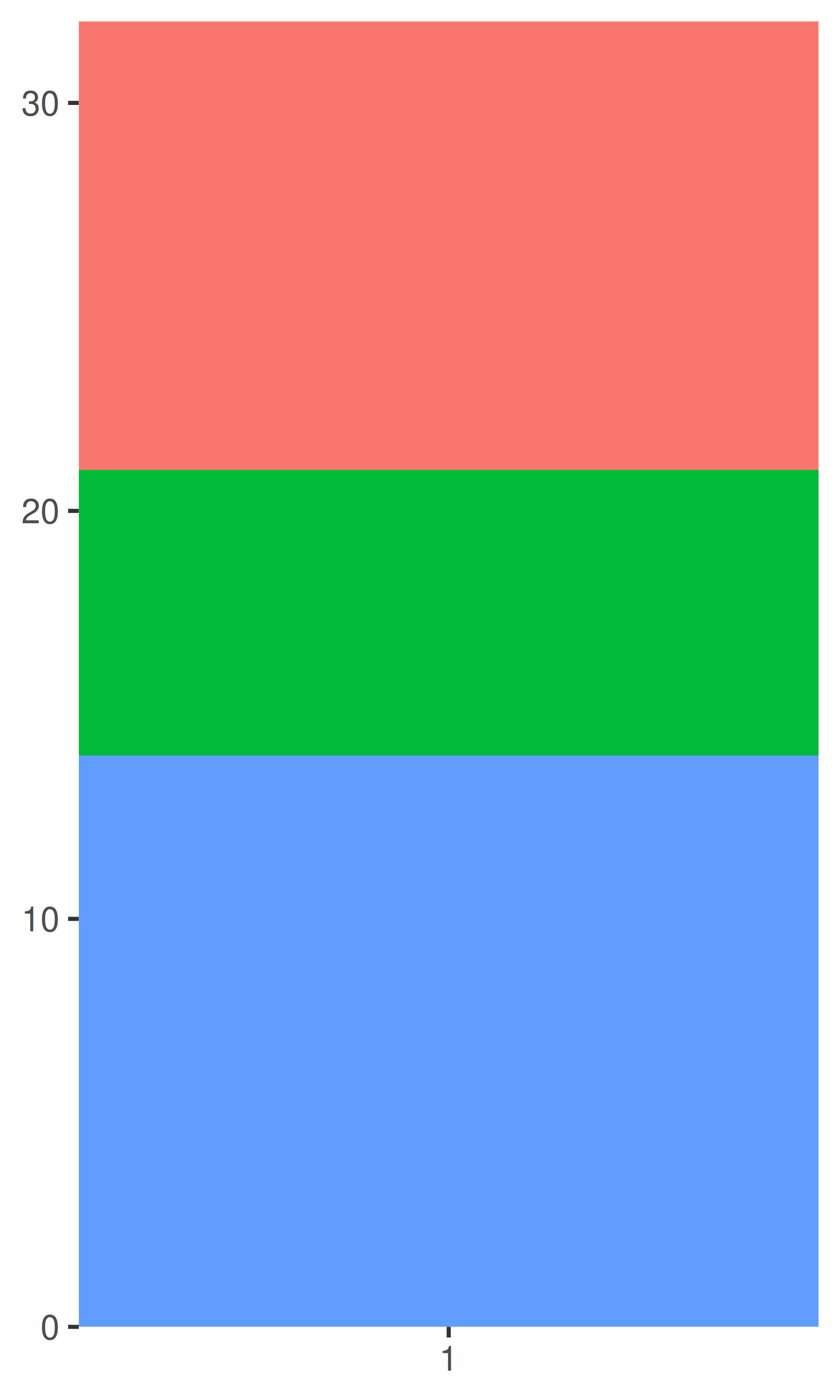

15.2.3 Proyecciones cartográficas con coord_map()

Los mapas son intrínsecamente visualizaciones de datos esféricos. Simplemente trazar longitudes y latitudes sin procesar es engañoso, por lo que debemos proyectar los datos. Hay dos formas de hacer esto con ggplot2:

  • coord_quickmap() es una aproximación rápida y sucia que establece la relación de aspecto para garantizar que 1 m de latitud y 1 m de longitud estén a la misma distancia en el medio de la gráfica. Este es un punto de partida razonable para regiones más pequeñas y es muy rápido.

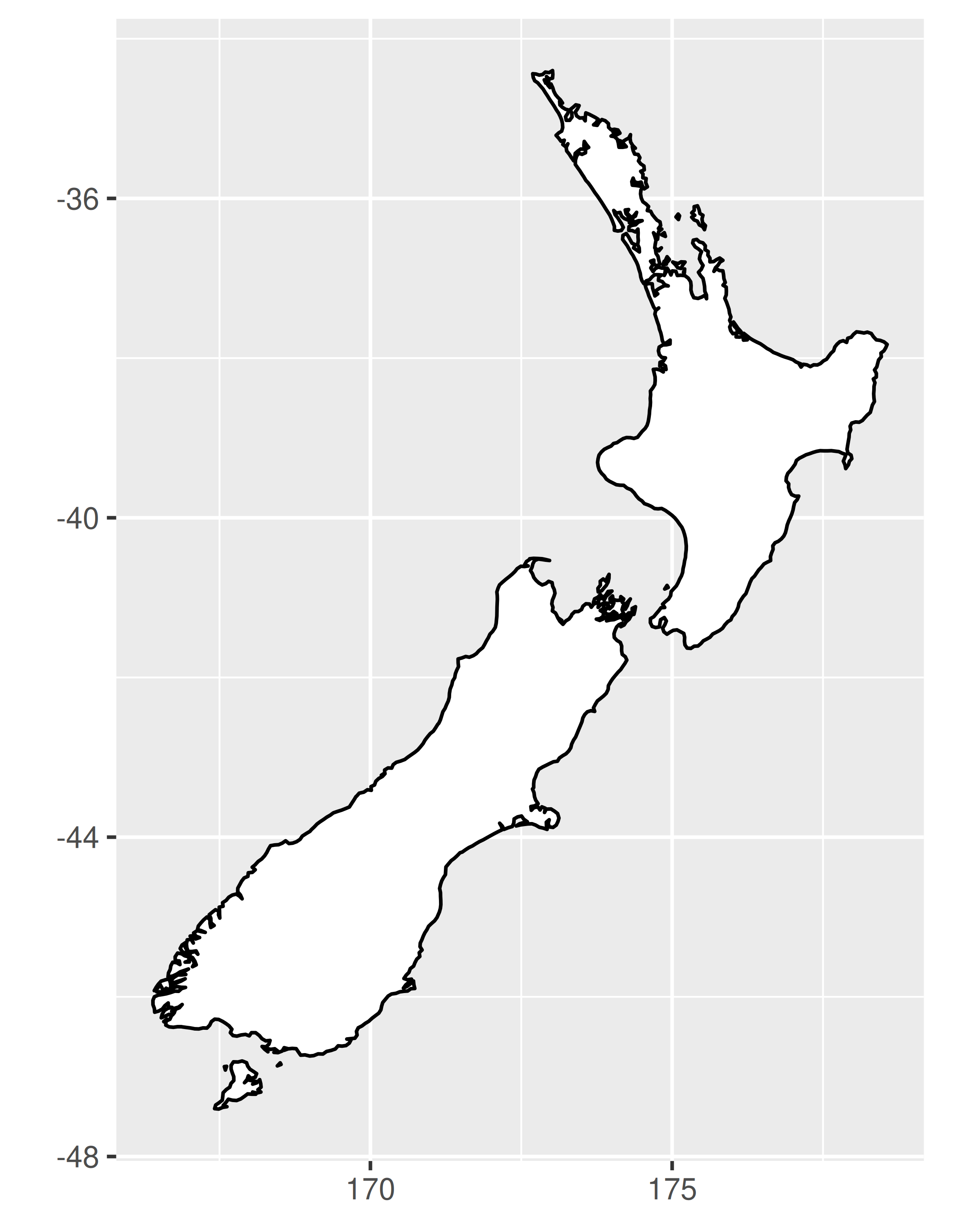
    # Preparar un mapa de Nueva Zelanda
nzmap <- ggplot(map_data("nz"), aes(long, lat, group = group)) +
  geom_polygon(fill = "white", colour = "black") +
  xlab(NULL) + ylab(NULL)

# Trazarlo en coordenadas cartesianas
nzmap
# Con la aproximación de la relación de aspecto
nzmap + coord_quickmap()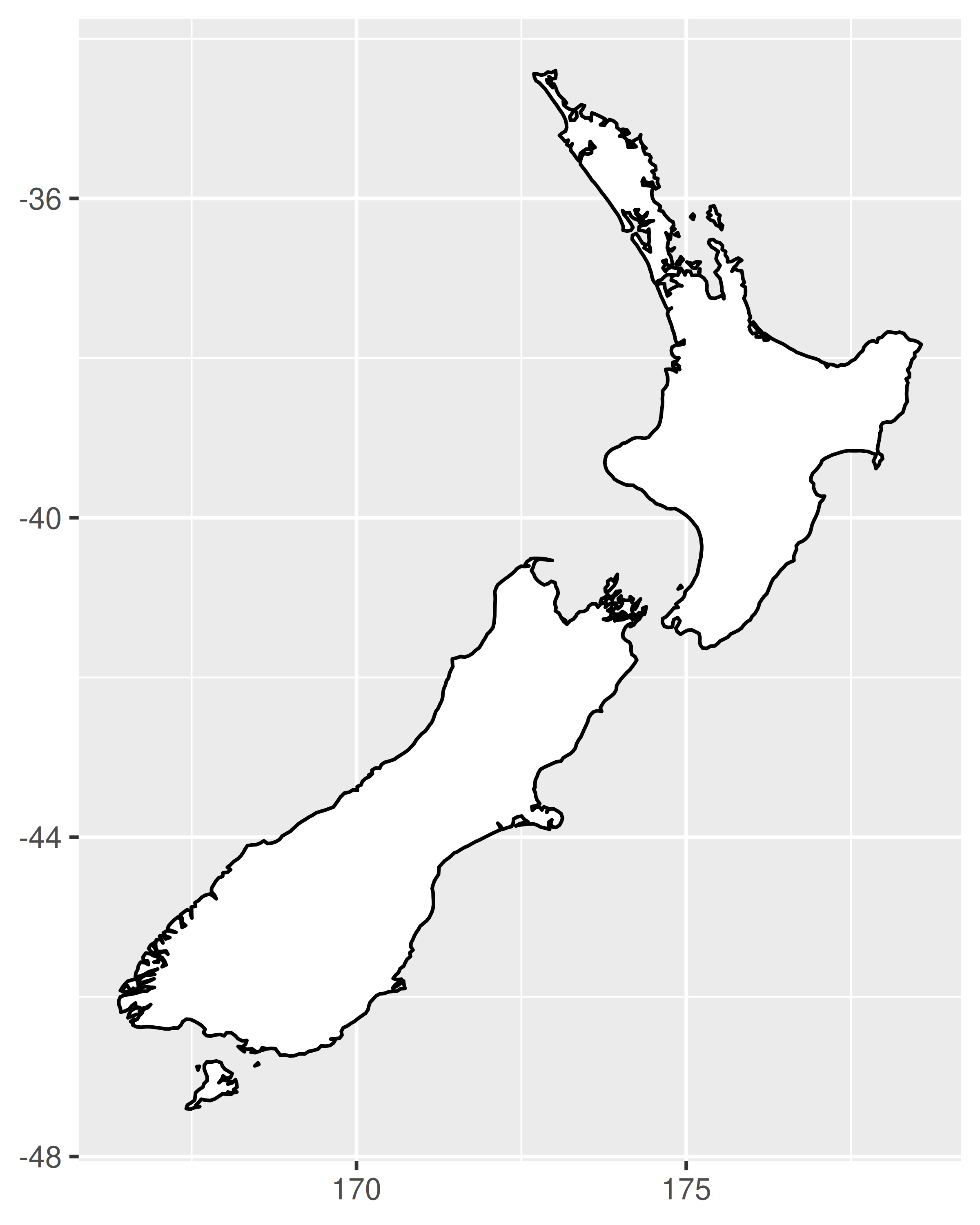

  • coord_map() utiliza el paquete mapproj, https://cran.r-project.org/package=mapproj para hacer una proyección cartográfica formal. Toma los mismos argumentos que mapproj::mapproject() para controlar la proyección. Es mucho más lento que coord_quickmap() porque debe masticar los datos y transformar cada pieza.

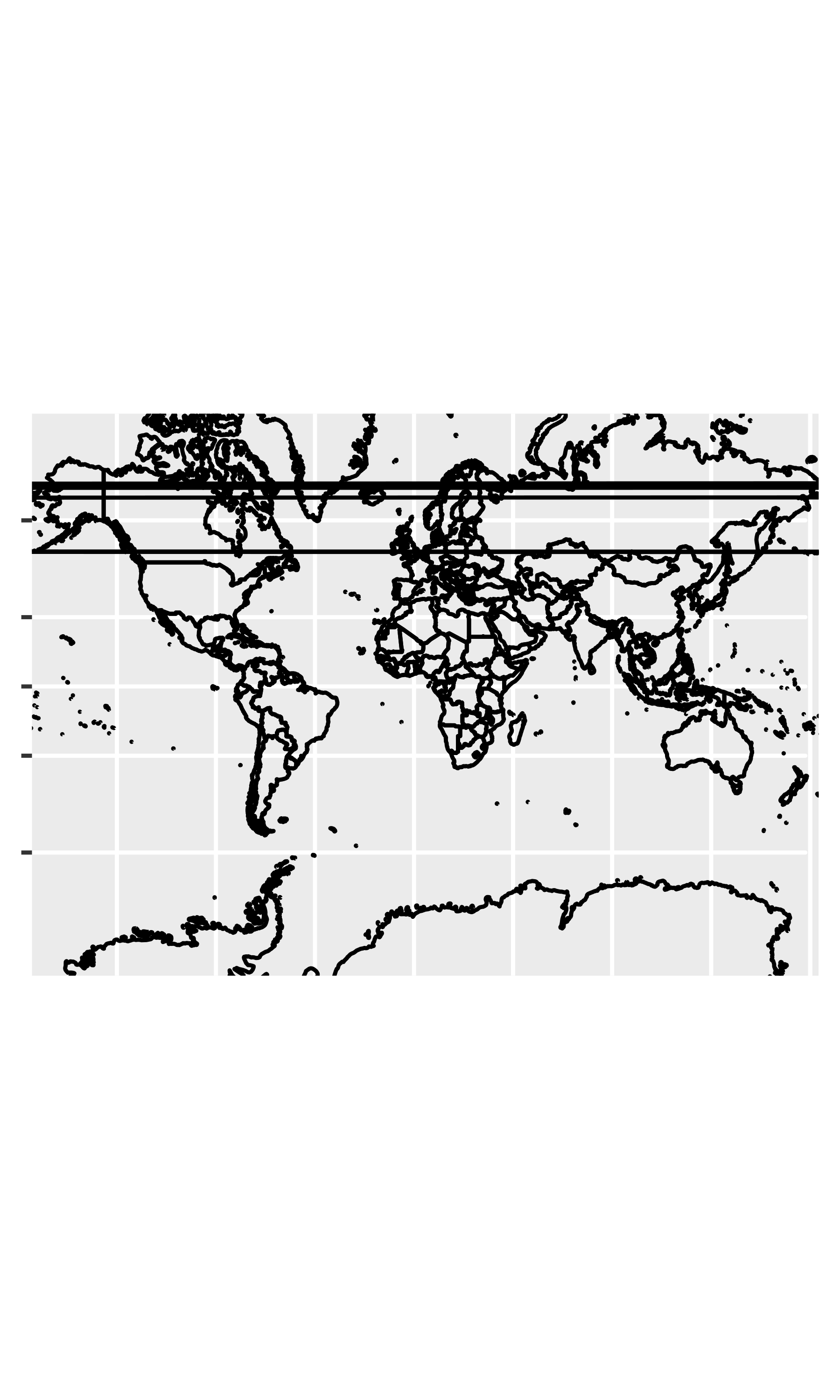
    world <- map_data("world")
worldmap <- ggplot(world, aes(long, lat, group = group)) +
  geom_path() +
  scale_y_continuous(NULL, breaks = (-2:3) * 30, labels = NULL) +
  scale_x_continuous(NULL, breaks = (-4:4) * 45, labels = NULL)

worldmap + coord_map()
# Algunas proyecciones más locas
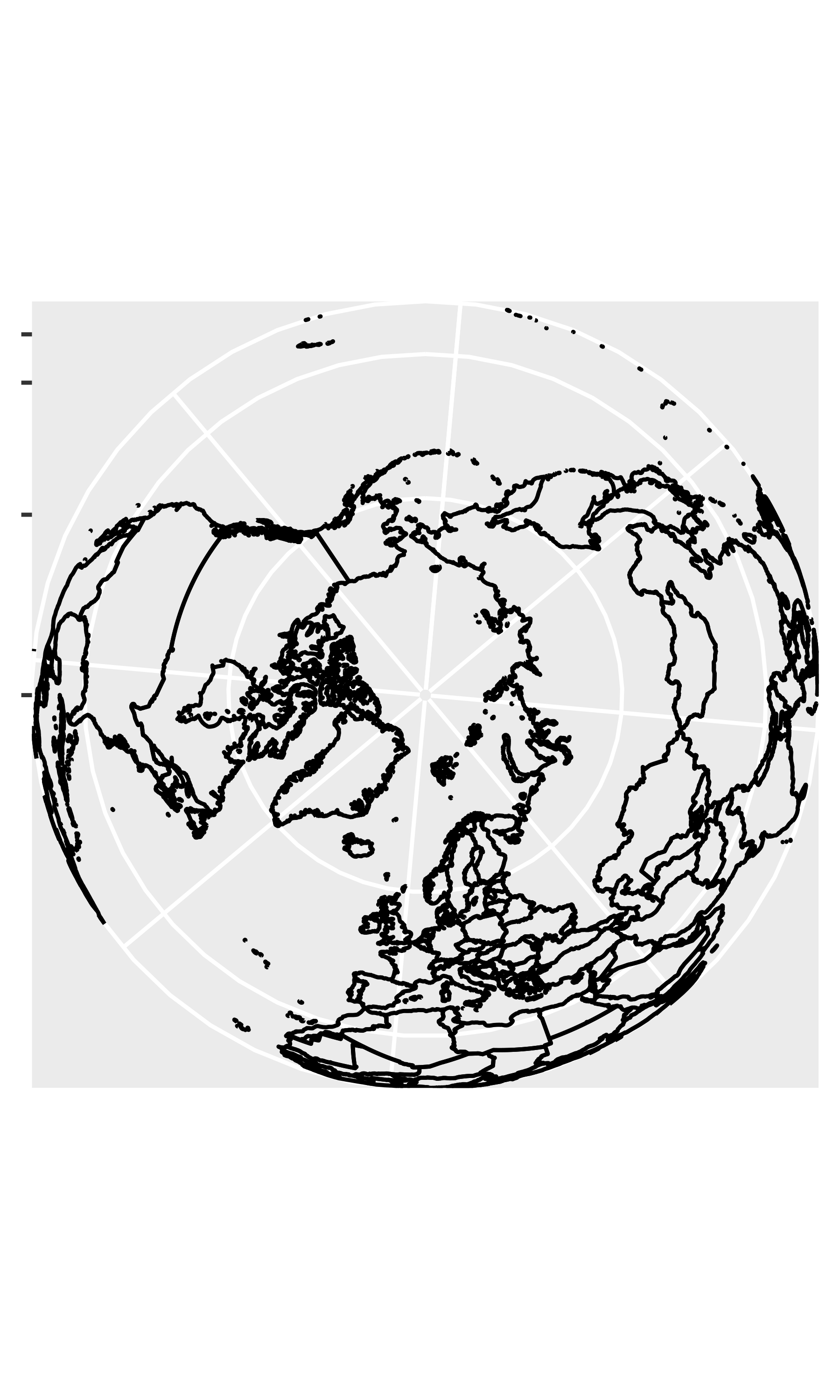
worldmap + coord_map("ortho")
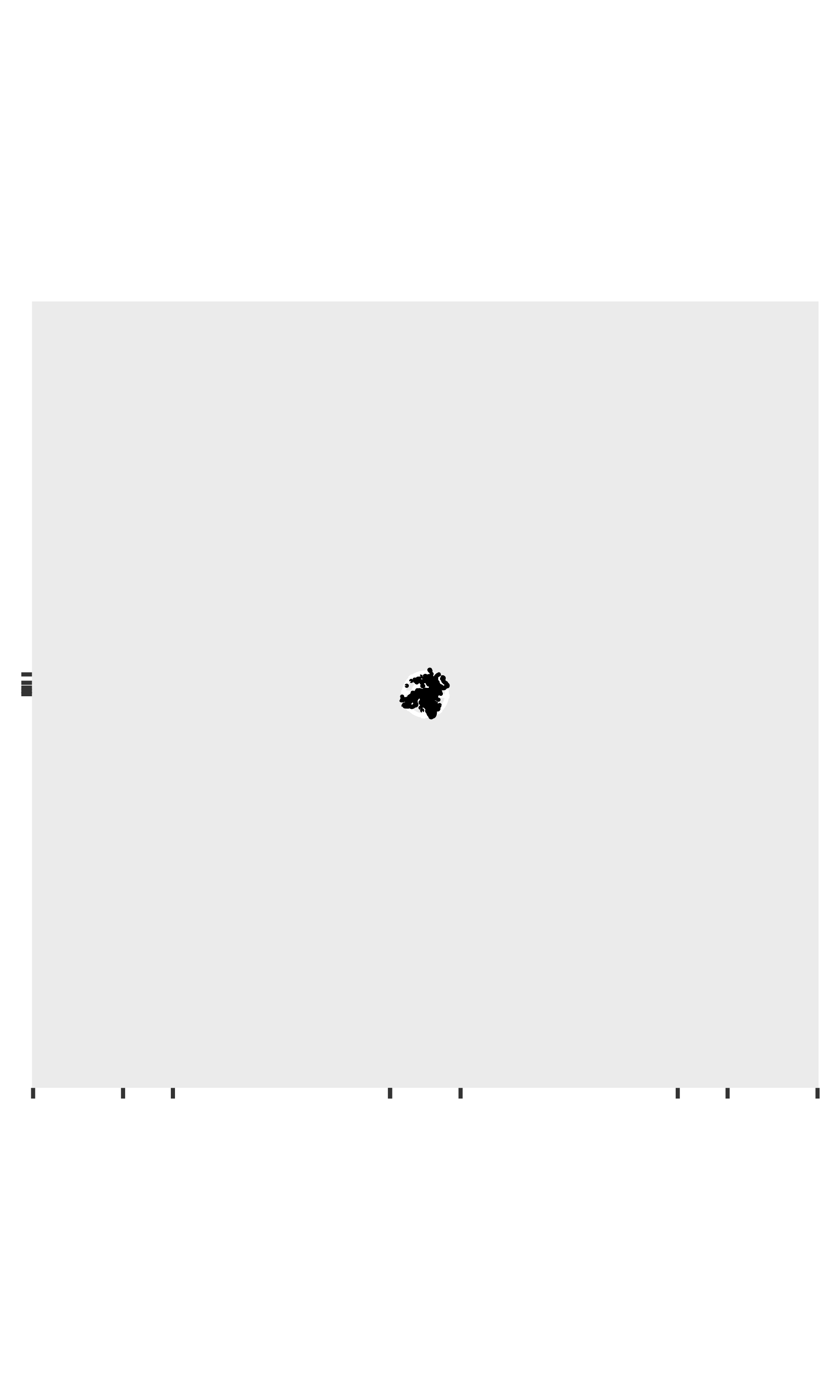
worldmap + coord_map("stereographic")