21  Un caso de estudio

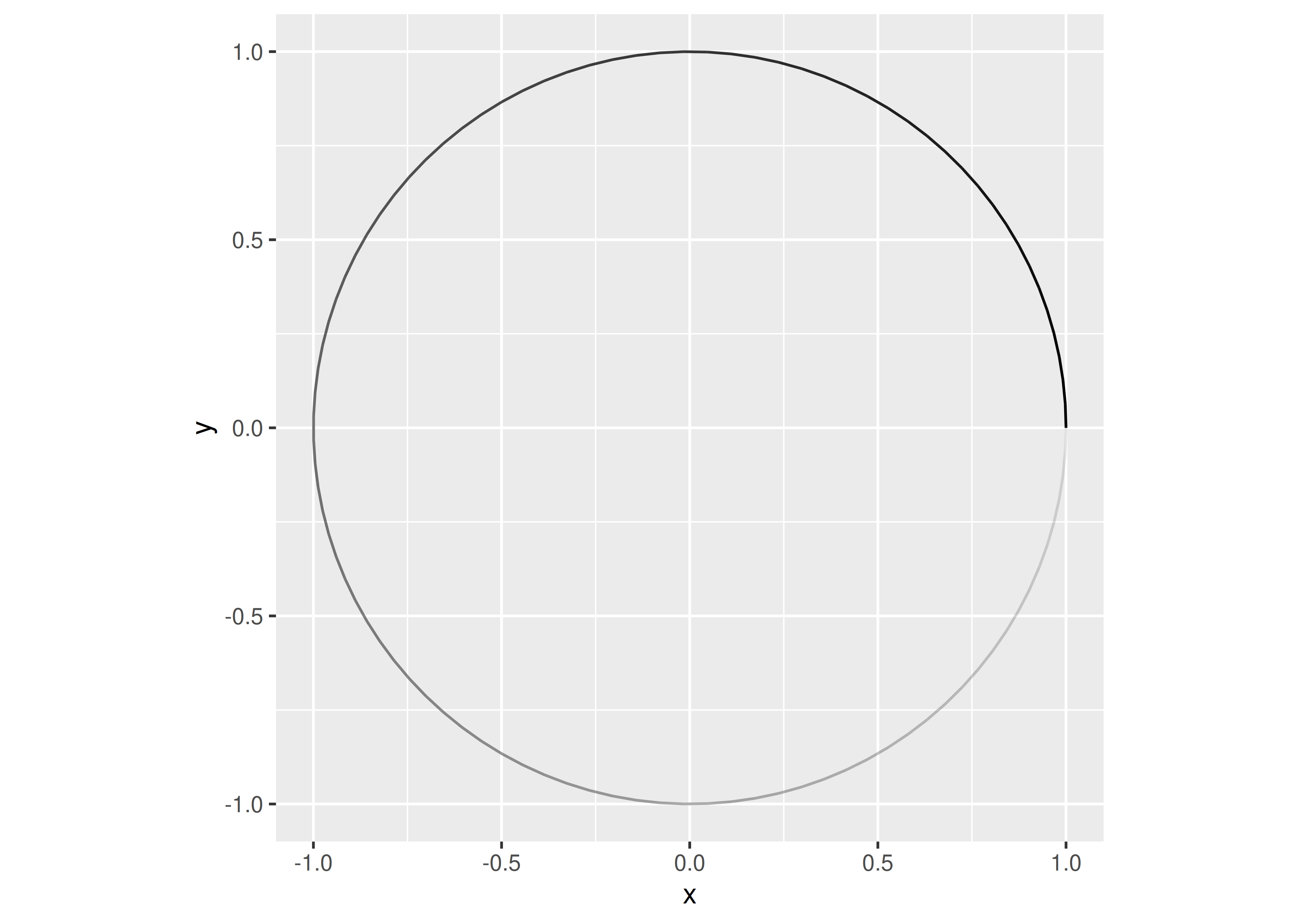
You are reading the work-in-progress third edition of the ggplot2 book. This chapter should be readable but is currently undergoing final polishing.

Capítulo 20 proporcionó una descripción general de alto nivel sobre la creación de extensiones de ggplot2, basándose en la discusión sobre los aspectos internos de ggplot2 en Capítulo 19. En este capítulo llevaremos ese conocimiento un paso más allá, brindando una inmersión más profunda en el proceso de desarrollo de extensiones con todas las funciones. Para hacer esto, tomaremos un solo ejemplo (construir una nueva geom que parece un resorte) y lo seguiremos durante todo el proceso de desarrollo.

Este es un ejemplo cuidadosamente elaborado. Es poco probable que desee utilizar resortes para visualizar sus datos, por lo que ggplot2 aún no proporciona una geom de resorte. Sin embargo, los resortes son lo suficientemente complicados como para ilustrar las partes más importantes del proceso. ¡Esto los hace ideales para nuestros propósitos!

Desarrollaremos la ampliación en cinco fases:

  1. Comenzaremos lo más simple posible usando el geom_path() existente, emparejándolo con una nueva estadística (Sección 21.2).
  2. La nueva estadística solo permite diámetro y tensión fijos, por lo que a continuación permitiremos que se utilicen por motivos estéticos (Sección 21.3).
  3. Una estadística es un excelente lugar para comenzar, pero tiene algunas restricciones fundamentales, por lo que a continuación convertiremos nuestro trabajo en una geom adecuada (Sección 21.4).
  4. Las geoms solo pueden usar dimensiones relativas a los datos y no pueden usar tamaños absolutos como 2 cm, por lo que a continuación te mostraremos cómo dibujar el resorte con una cuadrícula (Sección 21.6).
  5. Terminaremos proporcionando una escala personalizada y una leyenda para combinar con geom (Sección 21.7).

Una vez que haya recorrido este capítulo, le recomendamos encarecidamente que explore el código fuente de ggplot2 para ver cómo se implementan otras estadísticas y geoms. A menudo serán más complicados de lo que necesitas, pero te darán una idea de lo que puedes hacer.

21.1 ¿Qué es un resorte?

El desarrollo de una extensión generalmente comienza con una idea de lo que quieres dibujar. En este caso, queremos dibujar un resorte entre dos puntos, por lo que necesitamos algún código que dibuje un resorte que parezca plausible. Probablemente haya muchas formas de hacer esto, pero una sencilla es dibujar un círculo mientras se mueve el “bolígrafo” en una dirección. Aquí hay un conjunto de datos que define un círculo usando 100 puntos:

circle <- tibble(
  radians = seq(0, 2 * pi, length.out = 100),
  x = cos(radians),
  y = sin(radians),
  index = 1:100,
  type = "circle"
)

ggplot(circle, aes(x = x, y = y, alpha = -index)) + 
  geom_path(show.legend = FALSE) + 
  coord_equal()

Para transformar este círculo en un resorte que se extiende a lo largo del eje x usando dplyr, podríamos hacer algo como esto:

spring <- circle %>% 
  mutate(
    motion = seq(0, 1, length.out = 100),
    x = x + motion,
    type = "spring"
  )

ggplot(spring, aes(x = x, y = y, alpha = -index)) + 
  geom_path(show.legend = FALSE) + 
  coord_equal()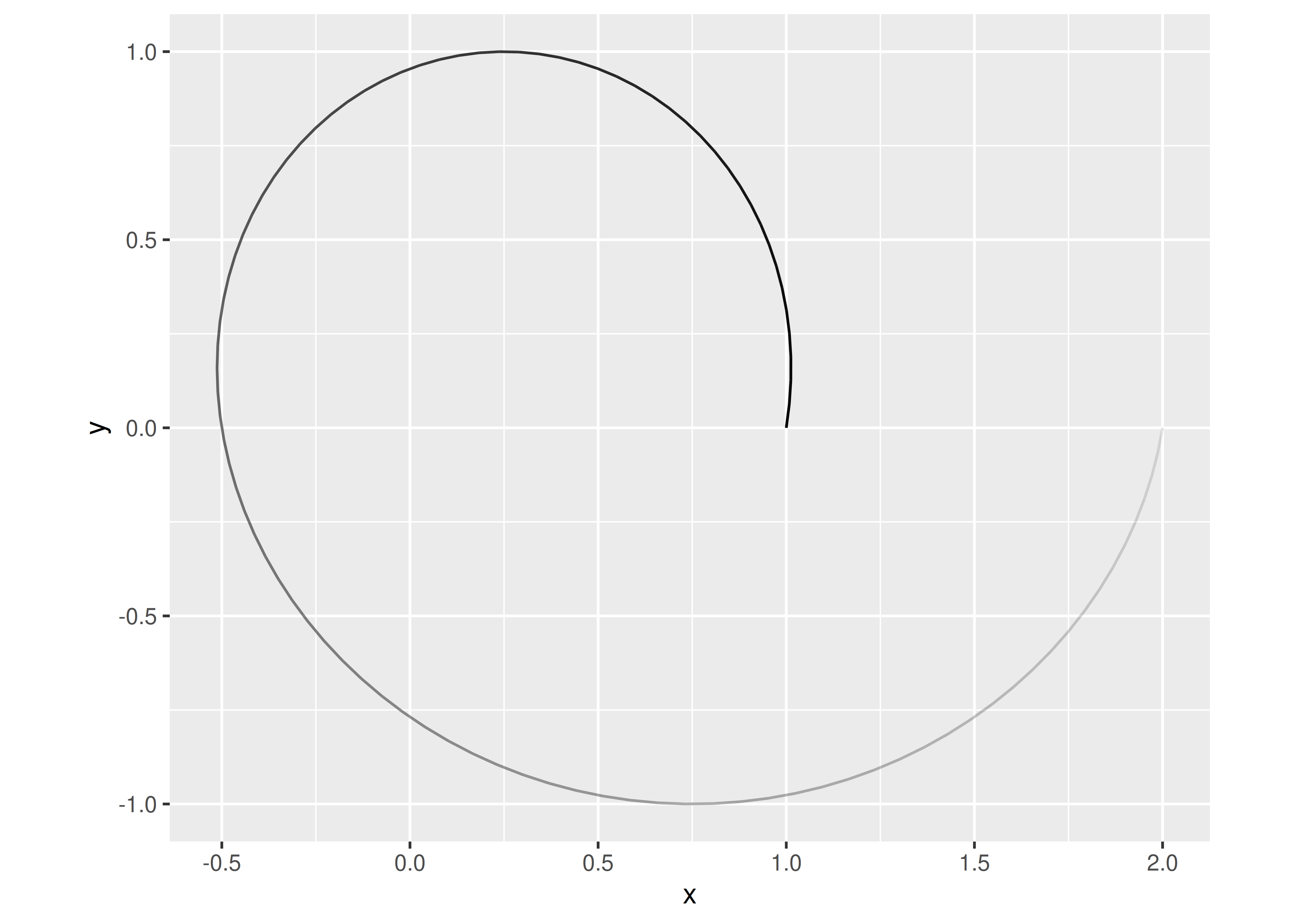

En este caso, nuestro “resorte” sólo ha dado vueltas una vez, y no se parece mucho a un resorte real, pero si siguiéramos trazando el círculo mientras nos movemos a lo largo del eje x, terminaríamos con un resorte con múltiples bucles. Cuanto más rápido movamos el “bolígrafo”, más estiraremos el resorte. Esto nos da una idea de los dos parámetros que caracterizan nuestros resortes:

  • El diameter del resorte, definido por el tamaño del círculo.
  • La tension del resorte, definida por la rapidez con la que nos movemos a lo largo de x.

Aunque probablemente esta no sea una parametrización físicamente correcta de los resortes en el mundo real, es lo suficientemente buena para nuestros propósitos.

Ahora que tenemos un método para dibujar resortes, vale la pena dedicar un poco de tiempo a pensar en lo que requerirá una geom basada en este método. El código que hemos escrito hasta este punto está perfectamente bien para un solo gráfico, pero hay nuevas preguntas a considerar al crear una extensión:

  • ¿Cómo especificaremos el diámetro de un resorte?
  • ¿Cómo mantenemos los círculos circulares incluso cuando cambiamos la relación de aspecto de la gráfica?
  • ¿Podemos asignar diámetro y tensión a variables en los datos?
  • ¿El diámetro y la tensión deberían ser parámetros que deben ser los mismos para todos los resortes en una capa o deberían ser una estética escalada que pueda variar de un resorte a otro?
  • Si planeamos distribuir nuestro spring geom a otros usuarios de R, ¿queremos depender del paquete dplyr?

Consideraremos estas preguntas a medida que avancemos en el capítulo.

21.2 Parte 1: una estadística

Comencemos a convertir esta idea en una extensión de ggplot2. Debido a que estamos creando una extensión que dibuja una nueva capa ggplot2, debemos decidir si el objeto ggproto que creamos debe ser Stat o Geom. Quizás sea sorprendente que esta decisión no esté guiada por si queremos terminar con geom_spring() o stat_spring(): hay muchas extensiones Stat que se usan a través de un constructor geom_*() . Una mejor manera de pensar en esta decisión es considerar si podemos usar una geom existente con datos transformados. En ese caso, podemos usar una Stat que suele ser más sencilla de codificar que una Geom.

El código que escribimos en la última sección se ajusta muy bien a esta descripción. Lo único que hacemos es dibujar un camino, pero damos vueltas en lugar de ir en línea recta. Eso sugiere que podemos usar una Stat que transforma los datos y luego usa GeomPath para encargarse del dibujo real.

21.2.1 Funcionalidad del edificio

Siempre que esté desarrollando una nueva Stat, una estrategia sensata es comenzar escribiendo la función de transformación de datos y luego, una vez que esté funcionando, incorporarla a un ggproto Stat. En este caso, vamos a necesitar una función create_spring() que tome un punto inicial, un punto final, un diámetro y una tensión. Más precisamente:

  • Nuestro punto de partida estará definido por los argumentos x e y.
  • Nuestro punto final estará definido por los argumentos xend y yend.
  • El argumento diameter se utilizará para escalar el tamaño de nuestro círculo.
  • Definir tension es un poco más complicado. La cantidad que realmente queremos expresar es “qué tan lejos se mueve el resorte en relación con el tamaño de los círculos”. Entonces definiremos tension para referirnos a la distancia total movida desde el punto inicial hasta el punto final, dividida por el tamaño de los círculos.1
  • También tendremos un parámetro n para dar el número de puntos utilizados por revolución, definiendo la fidelidad visual del resorte.

Ahora podemos escribir código para nuestra función create_spring():

create_spring <- function(x, 
                          y, 
                          xend, 
                          yend, 
                          diameter = 1, 
                          tension = 0.75, 
                          n = 50) {
  
  # Validar los argumentos de entrada.
  if (tension <= 0) {
    rlang::abort("`tension` debe ser mayor que cero.")
  }
  if (diameter == 0) {
    rlang::abort("`diameter` no puede ser cero.")
  }
  if (n == 0) {
    rlang::abort("`n` debe ser mayor que cero.")
  }
  
  # Calcule la longitud directa de la trayectoria del resorte
  length <- sqrt((x - xend)^2 + (y - yend)^2)
  
  # Calcular el número de revoluciones y puntos que necesitamos
  n_revolutions <- length / (diameter * tension)
  n_points <- n * n_revolutions
  
  # Calcule la secuencia de radianes y los valores de compensación de x e y
  radians <- seq(0, n_revolutions * 2 * pi, length.out = n_points)
  x <- seq(x, xend, length.out = n_points)
  y <- seq(y, yend, length.out = n_points)
  
  # Crear y devolver el marco de datos transformado.
  data.frame(
    x = cos(radians) * diameter/2 + x,
    y = sin(radians) * diameter/2 + y
  )
}

Esta función conserva la lógica del código Spring que escribimos en Sección 21.1, pero hace algunas cosas nuevas que son muy importantes al escribir extensiones:

  • Es preciso al especificar los parámetros que definen el resorte.
  • Comprueba explícitamente la entrada y utiliza rlang::abort() para generar un error si el usuario pasa un valor no válido a la función.
  • Utiliza funciones base R para hacer el trabajo: no hay código dplyr en esta función porque no queremos que nuestra Stat dependa de dplyr.2

Lo bueno de escribir create_spring() como función es que podemos probarla3 para convencernos de que la lógica funciona:

spring <- create_spring(
  x = 4, y = 2, xend = 10, yend = 6,
  diameter = 2, tension = 0.6, n = 50
)

ggplot(spring) + 
  geom_path(aes(x = x, y = y)) + 
  coord_equal()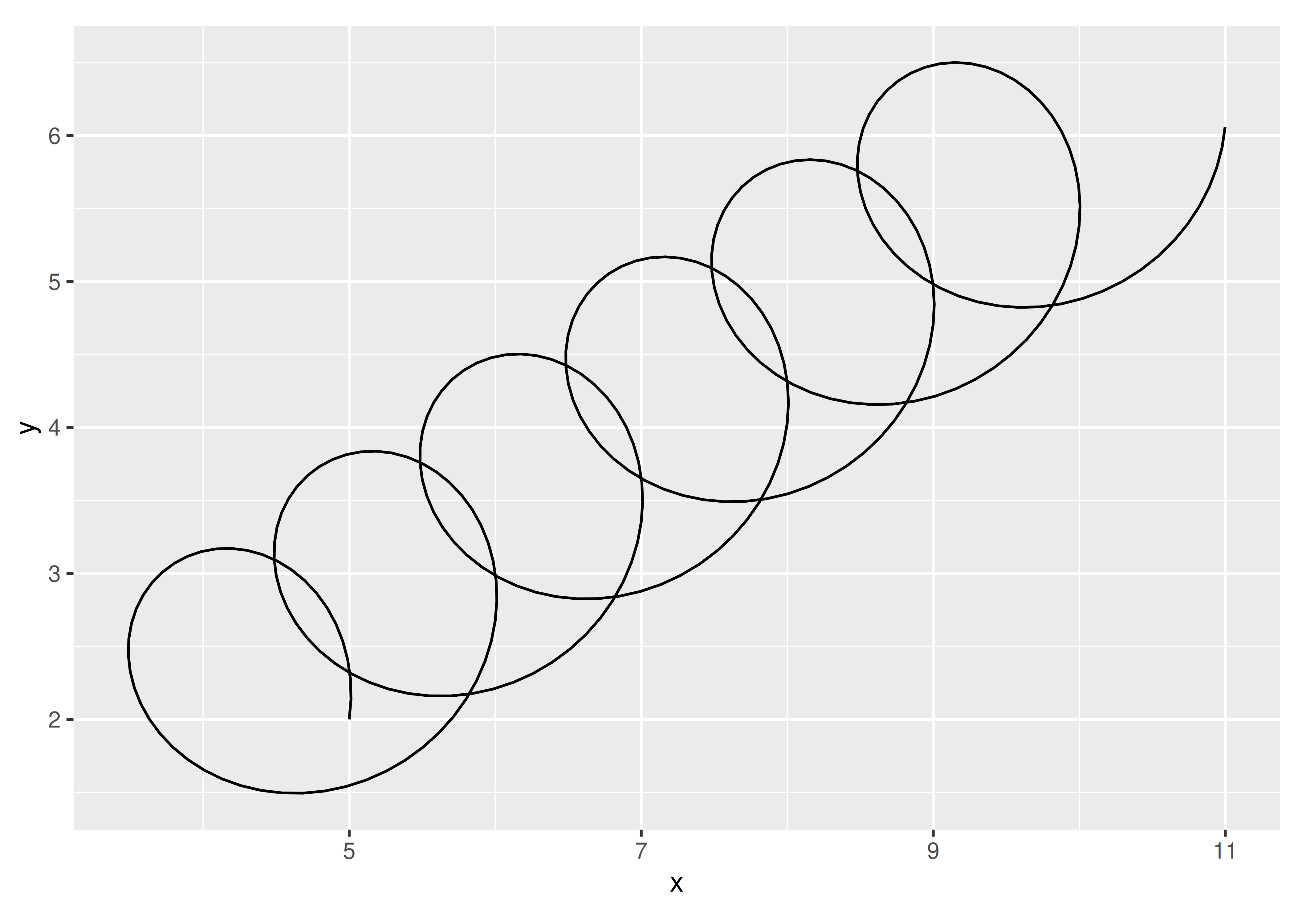

21.2.2 Creando la estadística

Ahora que tenemos nuestra función de transformación, nuestra siguiente tarea es encapsularla en una Stat. Para hacer esto, tomaremos lo que aprendimos sobre la creación de objetos Stat en Sección 20.2 y lo ampliaremos un poco. Nuestro primer paso es escribir un código que cree una subclase de Stat a la que llamaremos StatSpring:

StatSpring <- ggproto("StatSpring", Stat)

Esto crea una nueva subclase Stat llamada StatSpring. Esta clase no hace nada interesante en este momento: lo único que hace este código hasta ahora es darle un nombre a la clase.4 Para que esto sea útil, necesitaremos especificar los métodos que incorporar la funcionalidad que deseamos. En Sección 20.2 creamos una Stat anulando el método predeterminado compute_group() y el campo predeterminado para required_aes,5 pero los objetos Stat tienen muchas propiedades que puedes modificar. Si imprimimos el objeto Stat, podemos ver una lista de esas propiedades:

Stat
#> <ggproto object: Class Stat, gg>
#>     aesthetics: function
#>     compute_group: function
#>     compute_layer: function
#>     compute_panel: function
#>     default_aes: uneval
#>     dropped_aes: 
#>     extra_params: na.rm
#>     finish_layer: function
#>     non_missing_aes: 
#>     optional_aes: 
#>     parameters: function
#>     required_aes: 
#>     retransform: TRUE
#>     setup_data: function
#>     setup_params: function

Puedes modificar casi cualquiera de estos: los únicos que no debes tocar son aesthetics y parameters, que están destinados únicamente para uso interno.

Para nuestro ejemplo de StatSpring, los tres métodos/campos que necesitaremos especificar son setup_data(), compute_panel() y required_aes. Analizaremos esto con más detalle en la siguiente sección, pero para ayudarlo a ver a qué apuntamos, aquí está el código completo de nuestra estadística:

StatSpring <- ggproto("StatSpring", Stat, 
  
  # Edite los datos de entrada para garantizar que los identificadores de grupo sean únicos
  setup_data = function(data, params) {
    if (anyDuplicated(data$group)) {
      data$group <- paste(data$group, seq_len(nrow(data)), sep = "-")
    }
    data
  },
  
  # Construya datos para este panel llamando a create_spring()
  compute_panel = function(data, 
                           scales, 
                           diameter = 1, 
                           tension = 0.75, 
                           n = 50) {
    cols_to_keep <- setdiff(names(data), c("x", "y", "xend", "yend"))
    springs <- lapply(
      seq_len(nrow(data)), 
      function(i) {
        spring_path <- create_spring(
          data$x[i], 
          data$y[i], 
          data$xend[i], 
          data$yend[i], 
          diameter = diameter, 
          tension = tension, 
          n = n
        )
        cbind(spring_path, unclass(data[i, cols_to_keep]))
      }
    )
    do.call(rbind, springs)
  },
  
  # Especificar qué estética se requiere entrada
  required_aes = c("x", "y", "xend", "yend")
)

WPodemos imprimir cualquiera de estos métodos con un comando como StatSpring$compute_panel o StatSpring$setup_data.

21.2.3 Métodos

Echemos un vistazo más de cerca a los métodos definidos para nuestro StatSpring. Como se analiza en Sección 20.2, los métodos más importantes para una estadística son los tres métodos compute_*. Siempre se debe definir uno de estos, generalmente compute_group() o compute_panel(). Como regla general, si la estadística opera en varias filas, comenzamos implementando un método compute_group(), y si la estadística opera en filas individuales, implementamos un método compute_panel(). Nuestra estadística de resorte es del último tipo: cada resorte está definido por una sola fila de datos originales, por lo que usaremos el método compute_panel() que recibe todos los datos de un solo panel.

Como puedes ver al mirar el código fuente de nuestro método compute_panel(), estamos haciendo un poco más que simplemente llamar a nuestra función create_spring():

function(data, scales, diameter = 1, tension = 0.75, n = 50) {
  cols_to_keep <- setdiff(names(data), c("x", "y", "xend", "yend"))
  springs <- lapply(
    seq_len(nrow(data)), 
    function(i) {
      spring_path <- create_spring(
        data$x[i], 
        data$y[i], 
        data$xend[i], 
        data$yend[i], 
        diameter = diameter, 
        tension = tension, 
        n = n
      )
      cbind(spring_path, unclass(data[i, cols_to_keep]))
    }
  )
  do.call(rbind, springs)
}

Usamos lapply() para recorrer cada fila de datos y crear los puntos necesarios para dibujar el resorte correspondiente. Para cada uno de estos resortes, usamos cbind() para combinar los datos del resorte con todas las columnas que no son de posición de la fila de entrada. Esto es muy importante, ya que de lo contrario las asignaciones estéticas a p.e. El color y el tamaño se perderían. Finalmente, debido a que la salida de lapply() es una lista de marcos de datos (uno por primavera), usamos rbind() para combinarlos en un único marco de datos que se devuelve.

Al definir una nueva estadística, es muy común especificar uno o ambos métodos setup_data() y setup_params(). Estos métodos se invocan al principio del proceso de construcción de la gráfica, por lo que puede utilizarlos para realizar comprobaciones y modificaciones tempranas de los parámetros y datos.

Para nuestro ejemplo StatSpring, utilizamos el método setup_data() para garantizar que cada fila de entrada tenga una estética de grupo única. Esto es importante porque vamos a dibujar nuestros resortes con GeomPath y debemos asegurarnos de que el marco de datos generado por la estadística tenga un identificador único para cada resorte. Al hacerlo, se garantiza que la geom dibuje cada resorte como un camino distinto y no dibuje ninguna línea de conexión entre diferentes resortes. Nuevamente, hay algunos detalles sutiles sobre los que llamar la atención en la implementación:

function(data, params) {
  if (anyDuplicated(data$group)) {
    data$group <- paste(data$group, seq_len(nrow(data)), sep = "-")
  }
  data
}

Tenga en cuenta que esta implementación conserva el valor original de data$group y agrega una identificación única si es necesario. Esto es importante porque la estética del grupo a veces se utiliza para transportar metadatos y no queremos perder esa información.

La parte final de nuestra nueva clase es el campo required_aes. Este es un vector de caracteres que proporciona los nombres de la estética que el usuario debe proporcionar a la estadística. En este caso, debemos asegurarnos de que el usuario especifique cuatro posiciones estéticas: x e y definen dónde comienza el resorte, mientras que xend y yend definen dónde termina. El campo required_aes, junto con default_aes y non_missing_aes, también define la estética que comprende esta estadística. Cualquier estética que no aparezca en estos campos (o en los campos del geom correspondiente) generará una advertencia y el mapeo será ignorado.

21.2.4 Constructores

Ahora que tenemos nuestro objeto ggproto StatSpring, es hora de escribir funciones constructoras con las que el usuario interactuará. Estrictamente hablando, no necesitamos hacer esto, porque geom_path(stat = "spring") ya funcionará, pero es una buena práctica escribir funciones constructoras para comodidad de los usuarios. Además, la función constructora proporciona un buen lugar para documentar la nueva funcionalidad.

Quizás sea sorprendente que los objetos de estadísticas casi siempre estén emparejados con un constructor geom_*() porque la mayoría de los usuarios de ggplot2 están acostumbrados a agregar geoms, no estadísticas, cuando construyen una gráfica. El constructor en sí es principalmente código repetitivo que envuelve una llamada a layer(); solo tenga cuidado de hacer coincidir el orden de los argumentos y los nombres utilizados en los constructores de ggplot2 para no sorprender a sus usuarios.

geom_spring <- function(mapping = NULL,
                        data = NULL, 
                        stat = "spring",
                        position = "identity", 
                        ..., 
                        diameter = 1, 
                        tension = 0.75,
                        n = 50, 
                        arrow = NULL, 
                        lineend = "butt", 
                        linejoin = "round",
                        na.rm = FALSE, 
                        show.legend = NA, 
                        inherit.aes = TRUE
                        ) {
  layer(
    data = data,
    mapping = mapping,
    stat = stat,
    geom = GeomPath,
    position = position,
    show.legend = show.legend,
    inherit.aes = inherit.aes,
    params = list(
      diameter = diameter,
      tension = tension,
      n = n,
      arrow = arrow,
      lineend = lineend,
      linejoin = linejoin,
      na.rm = na.rm,
      ...
    )
  )
}

Para que esté completo, también debes crear una función constructora stat_*(). No hay sorpresas aquí: stat_spring() es muy similar a geom_spring() excepto que proporciona una geom predeterminada en lugar de una estadística predeterminada.

stat_spring <- function(mapping = NULL, 
                        data = NULL, 
                        geom = "path", 
                        position = "identity", 
                        ..., 
                        diameter = 1, 
                        tension = 0.75, 
                        n = 50, 
                        na.rm = FALSE, 
                        show.legend = NA, 
                        inherit.aes = TRUE) {
  layer(
    data = data, 
    mapping = mapping, 
    stat = StatSpring, 
    geom = geom, 
    position = position, 
    show.legend = show.legend, 
    inherit.aes = inherit.aes, 
    params = list(
      diameter = diameter, 
      tension = tension, 
      n = n, 
      na.rm = na.rm, 
      ...
    )
  )
}

21.2.5 Probando la estadística

Ahora que todo está en su lugar, podemos probar nuestra nueva capa:

df <- tibble(
  x = runif(5, max = 10),
  y = runif(5, max = 10),
  xend = runif(5, max = 10),
  yend = runif(5, max = 10),
  class = sample(letters[1:2], 5, replace = TRUE)
)

ggplot(df) + 
  geom_spring(aes(x = x, y = y, xend = xend, yend = yend)) +
  coord_equal()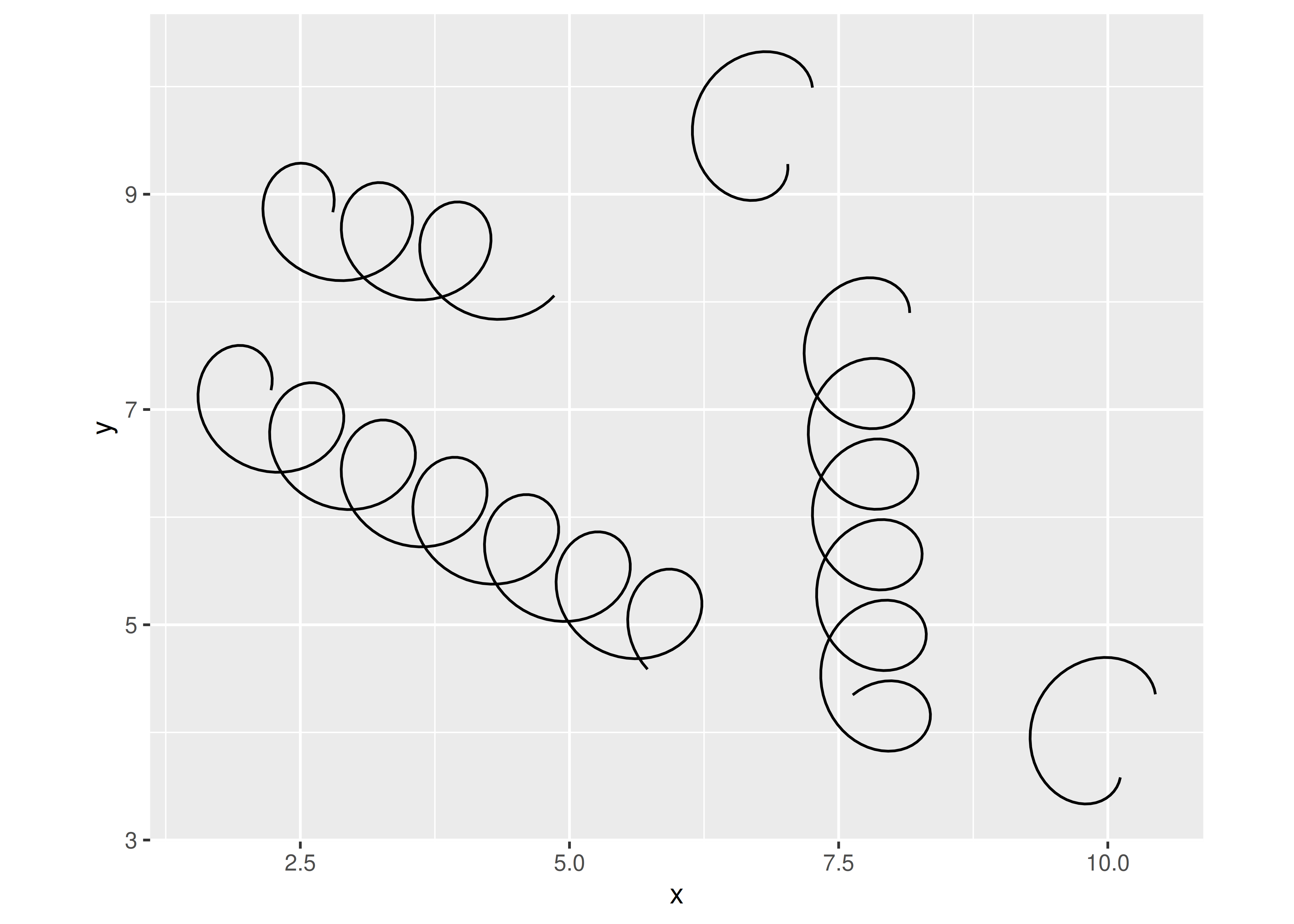

Esto se ve bastante bien. Los usuarios pueden llamar a nuestra función constructora geom_spring() y obtener resultados sensatos. Mejor aún, debido a que hemos escrito una nueva estadística, obtenemos una serie de funciones de forma gratuita, como escalado y facetado:

ggplot(df) + 
  geom_spring(
    aes(x, y, xend = xend, yend = yend, colour = class),
    linewidth = 1
  ) +
  coord_equal() + 
  facet_wrap(~ class)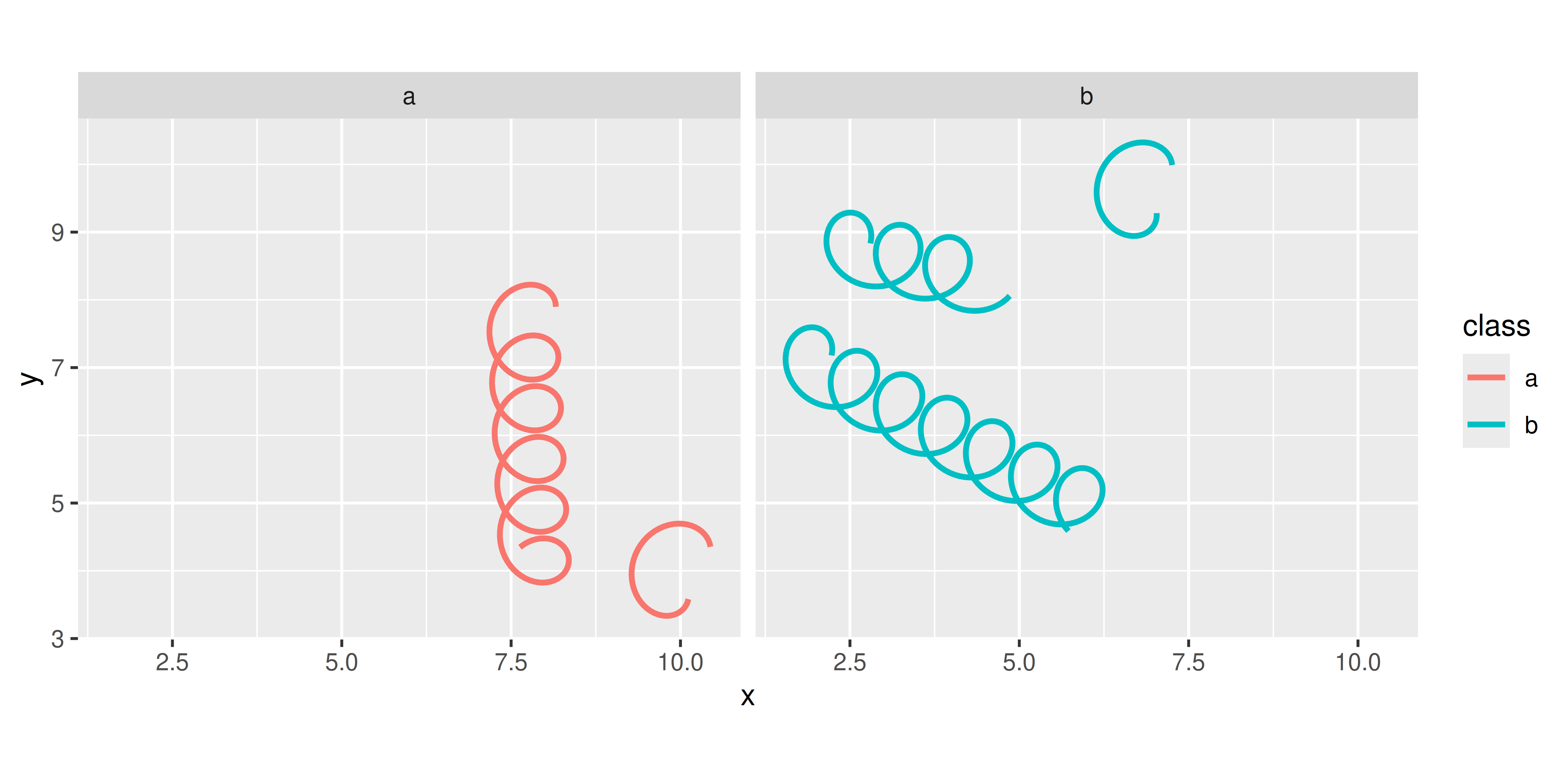

Los usuarios también tienen la opción de llamar al constructor stat_spring(), lo que puede ser útil si por alguna razón quieren dibujar los resortes con puntos en lugar de rutas:

ggplot(df) + 
  stat_spring(
    aes(x, y, xend = xend, yend = yend, colour = class),
    geom = "point", 
    n = 15
  ) +
  coord_equal() + 
  facet_wrap(~ class)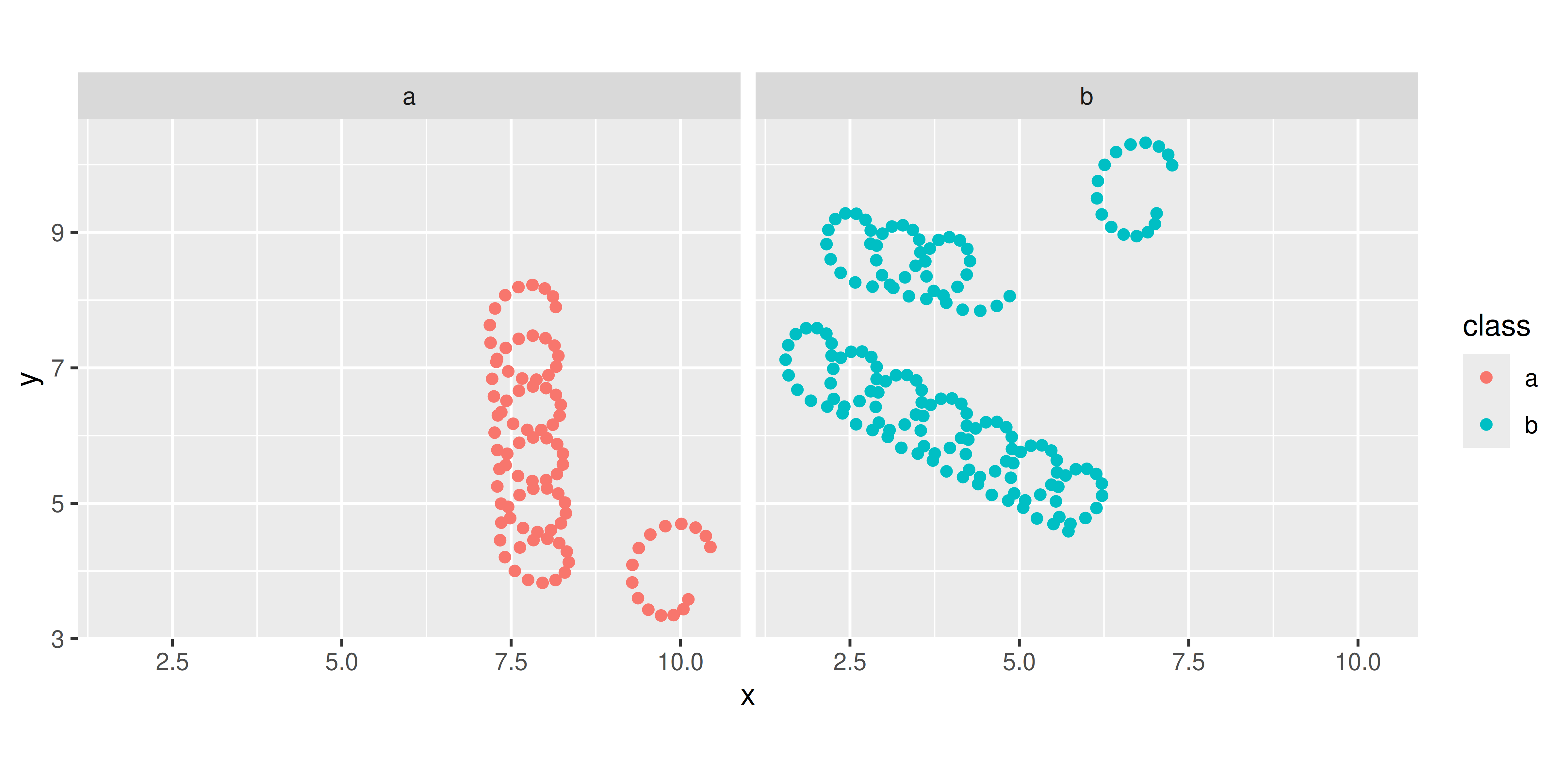

21.2.6 Post mortem

Ahora hemos creado con éxito nuestra primera extensión. Funciona, pero tiene algunas limitaciones en las que ahora debemos pensar.

Una desventaja de nuestra implementación es que el diámetro y la tensión son constantes que sólo se pueden establecer para la capa completa. Estas configuraciones se parecen más a la estética y sería bueno si sus valores pudieran asignarse a una variable en los datos. Discutiremos soluciones a este problema en Sección 21.3 y Sección 21.4.

21.3 Part 2: Añadiendo estética

La estadística que creamos en la última sección trata el diameter y la tension como argumentos constantes: no son estéticos y el usuario no puede asignarlos a una variable en los datos. Podemos solucionar este problema realizando algunos pequeños cambios en el código StatSpring:

StatSpring <- ggproto("StatSpring", Stat,
                      
  setup_data = function(data, params) {
    if (anyDuplicated(data$group)) {
      data$group <- paste(data$group, seq_len(nrow(data)), sep = "-")
    }
    data
  },
  
  compute_panel = function(data, scales, n = 50) {
    cols_to_keep <- setdiff(names(data), c("x", "y", "xend", "yend"))
    springs <- lapply(seq_len(nrow(data)), function(i) {
      spring_path <- create_spring(
        data$x[i], 
        data$y[i], 
        data$xend[i], 
        data$yend[i], 
        data$diameter[i],
        data$tension[i], 
        n
      )
      cbind(spring_path, unclass(data[i, cols_to_keep]))
    })
    do.call(rbind, springs)
  },
  
  required_aes = c("x", "y", "xend", "yend"),
  optional_aes = c("diameter", "tension")
)

La principal diferencia con nuestro intento anterior es que los argumentos diameter y tension de compute_panel() han desaparecido y ahora se toman de los datos (al igual que x, y, etc.) . Esto tiene un inconveniente que solucionaremos en Sección 21.4: ya no podemos establecer una estética fija. Debido a esto, necesitaremos eliminar esos argumentos de la función constructora:

geom_spring <- function(mapping = NULL, 
                        data = NULL, 
                        stat = "spring", 
                        position = "identity", 
                        ..., 
                        n = 50, 
                        arrow = NULL, 
                        lineend = "butt", 
                        linejoin = "round", 
                        na.rm = FALSE,
                        show.legend = NA, 
                        inherit.aes = TRUE) {
  layer(
    data = data, 
    mapping = mapping, 
    stat = stat, 
    geom = GeomPath, 
    position = position, 
    show.legend = show.legend, 
    inherit.aes = inherit.aes, 
    params = list(
      n = n, 
      arrow = arrow, 
      lineend = lineend, 
      linejoin = linejoin, 
      na.rm = na.rm, 
      ...
    )
  )
}

El constructor stat_spring() requeriría el mismo tipo de cambio.

Todo lo que queda es probar nuestra nueva implementación:

df <- tibble(
  x = runif(5, max = 10),
  y = runif(5, max = 10),
  xend = runif(5, max = 10),
  yend = runif(5, max = 10),
  class = sample(letters[1:2], 5, replace = TRUE),
  tension = runif(5),
  diameter = runif(5, 0.5, 1.5)
)

ggplot(df, aes(x, y, xend = xend, yend = yend)) + 
  geom_spring(aes(tension = tension, diameter = diameter))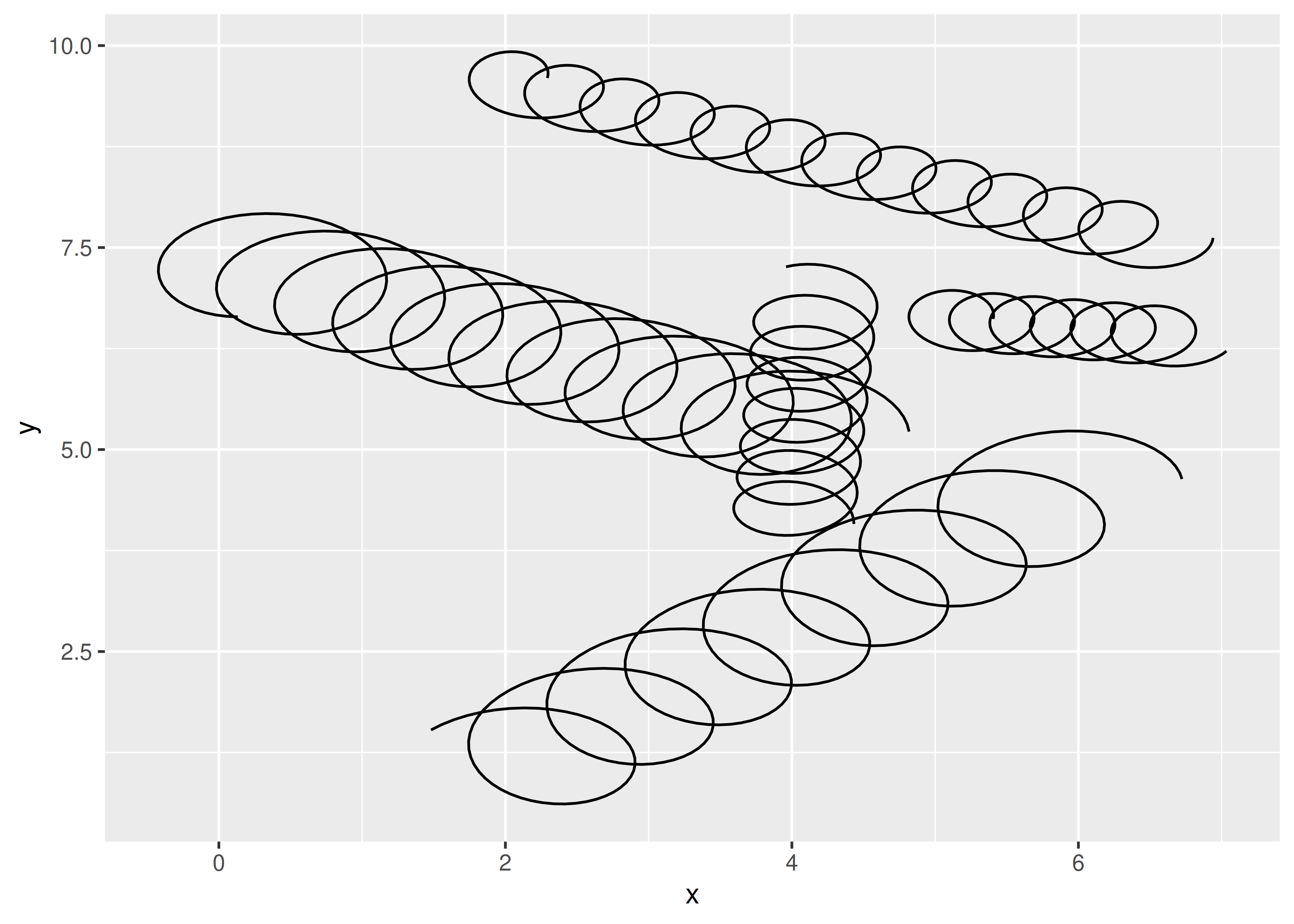

Parece funcionar. Sin embargo, como esperábamos, ya no es posible establecer diameter y tension como parámetros:

ggplot(df, aes(x, y, xend = xend, yend = yend)) + 
  geom_spring(diameter = 0.5)
#> Warning in geom_spring(diameter = 0.5): Ignoring unknown parameters: `diameter`
#> Warning: Computation failed in `stat_spring()`.
#> Caused by error in `if (tension <= 0) ...`:
#> ! argument is of length zero

21.3.1 Post mortem

En esta sección desarrollamos aún más nuestra estadística de resortes para que el diameter y la tension puedan usarse como estética, variando entre resortes. Desafortunadamente, existe un gran inconveniente: estas funciones ya no se pueden configurar globalmente. También nos falta una forma de controlar la escala de las dos estéticas. Solucionar ambos problemas requiere el mismo siguiente paso: alejar nuestra implementación de Stat y acercarla a una adecuada Geom.

21.4 Parte 3: Una geoma

En muchos casos, un enfoque centrado en las estadísticas es suficiente; por ejemplo, muchas de las primitivas gráficas proporcionadas por el paquete ggforce son estadísticas. Pero necesitamos ir más allá con la geom del resorte porque la estética de la tension y el diameter deben especificarse en unidades que no están relacionadas con el sistema de coordenadas. En consecuencia, reescribiremos nuestra geom para que sea una extensión Geom adecuada.

21.4.1 Extensiones de geom

Como se analizó en Capítulo 20, existen muchas similitudes entre las extensiones Stat y Geom. La mayor diferencia es que las extensiones Stat devuelven una versión modificada de los datos de entrada, mientras que las extensiones Geom devuelven objetos gráficos. En algunos casos, crear una nueva geom requiere que uses el paquete grid (cubriremos esto en Sección 21.6), pero a menudo no es necesario.

Al igual que los objetos de estadísticas, los objetos geom en ggproto tienen varios métodos y campos que puedes modificar. Puedes ver la lista imprimiendo el objeto:

Geom
#> <ggproto object: Class Geom, gg>
#>     aesthetics: function
#>     default_aes: uneval
#>     draw_group: function
#>     draw_key: function
#>     draw_layer: function
#>     draw_panel: function
#>     extra_params: na.rm
#>     handle_na: function
#>     non_missing_aes: 
#>     optional_aes: 
#>     parameters: function
#>     rename_size: FALSE
#>     required_aes: 
#>     setup_data: function
#>     setup_params: function
#>     use_defaults: function

21.4.2 Creando la geom

De la misma manera que una estadística usa los métodos compute_layer(), compute_panel() y compute_group() para transformar los datos, una geom usa draw_layer(), draw_panel() y draw_group() para crear representaciones gráficas de los datos. De la misma manera que creamos StatSpring escribiendo un método compute_panel() para hacer el trabajo pesado, crearemos GeomSpring escribiendo un método draw_panel():

GeomSpring <- ggproto("GeomSpring", Geom,
  
  # Asegúrese de que cada fila tenga una identificación de grupo única
  setup_data = function(data, params) {
    if (is.null(data$group)) {
      data$group <- seq_len(nrow(data))
    }
    if (anyDuplicated(data$group)) {
      data$group <- paste(data$group, seq_len(nrow(data)), sep = "-")
    }
    data
  },
  
  # Transforma los datos dentro del método draw_panel()
  draw_panel = function(data, 
                        panel_params, 
                        coord, 
                        n = 50, 
                        arrow = NULL,
                        lineend = "butt", 
                        linejoin = "round", 
                        linemitre = 10,
                        na.rm = FALSE) {
    
    # Transforme los datos de entrada para especificar las rutas del resorte.
    cols_to_keep <- setdiff(names(data), c("x", "y", "xend", "yend"))
    springs <- lapply(seq_len(nrow(data)), function(i) {
      spring_path <- create_spring(
        data$x[i], 
        data$y[i], 
        data$xend[i], 
        data$yend[i], 
        data$diameter[i],
        data$tension[i], 
        n
      )
      cbind(spring_path, unclass(data[i, cols_to_keep]))
    })
    springs <- do.call(rbind, springs)
    
    # Utilice el método draw_panel() de GeomPath para hacer el dibujo
    GeomPath$draw_panel(
      data = springs, 
      panel_params = panel_params, 
      coord = coord, 
      arrow = arrow, 
      lineend = lineend, 
      linejoin = linejoin, 
      linemitre = linemitre, 
      na.rm = na.rm
    )
  },
  
  # Especificar la estética predeterminada y requerida
  required_aes = c("x", "y", "xend", "yend"),
  default_aes = aes(
    colour = "black", 
    linewidth = 0.5, 
    linetype = 1L, 
    alpha = NA, 
    diameter = 1, 
    tension = 0.75
  )
)

A pesar de la extensión de este código, la mayor parte resulta familiar:

  • Los métodos setup_data() son esencialmente los mismos: en ambos casos garantizan que cada fila de los datos de entrada tenga un identificador de grupo único.

  • El método draw_panel() para nuestro objeto GeomSpring es muy similar al método compute_panel(). La principal diferencia es que nuestro método draw_panel() tiene un paso adicional: pasa las coordenadas del resorte calculadas a GeomPath$draw_panel(). Debido a que los manantiales son simplemente caminos elegantes, el método GeomPath$draw_panel() funciona perfectamente bien aquí.

  • A diferencia del código StatSpring que escribimos anteriormente, el código GeomSpring usa el campo default_aes para proporcionar valores predeterminados para cualquier estética que el usuario no especifique.

Un aspecto de este código puede sorprender a los desarrolladores que están acostumbrados al diseño orientado a objetos en otros lenguajes. Llamar directamente al método de un objeto afín, como lo hacemos cuando invocamos GeomPath$draw_panel() desde GeomSpring$draw_panel(), no se considera una buena práctica en otros sistemas orientados a objetos. Sin embargo, debido a que los objetos ggproto no tienen estado (Sección 19.4.5), esto es exactamente tan seguro como subclasificar GeomPath y llamar al método principal. Puede ver este enfoque en todas partes del código fuente de ggplot2.

21.4.3 un constructor

Al igual que en nuestros intentos anteriores, el paso final es escribir una función constructora geom_spring(). El código no es muy diferente a las versiones anteriores: usamos GeomSpring en lugar de GeomPath, y usamos la estadística de identidad en lugar de StatSpring.

geom_spring <- function(mapping = NULL, 
                        data = NULL, 
                        stat = "identity", 
                        position = "identity", 
                        ..., 
                        n = 50, 
                        arrow = NULL, 
                        lineend = "butt", 
                        linejoin = "round", 
                        na.rm = FALSE,
                        show.legend = NA, 
                        inherit.aes = TRUE) {
  layer(
    data = data, 
    mapping = mapping, 
    stat = stat, 
    geom = GeomSpring, 
    position = position, 
    show.legend = show.legend, 
    inherit.aes = inherit.aes, 
    params = list(
      n = n, 
      arrow = arrow, 
      lineend = lineend, 
      linejoin = linejoin, 
      na.rm = na.rm, 
      ...
    )
  )
}

21.4.4 Probando la geom

Ahora tenemos una geom adecuada con una estética predeterminada funcional y la capacidad de establecer la estética como parámetros:

ggplot(df, aes(x, y, xend = xend, yend = yend)) + 
  geom_spring(aes(tension = tension, diameter = diameter))
ggplot(df, aes(x, y, xend = xend, yend = yend)) + 
  geom_spring(diameter = 0.5)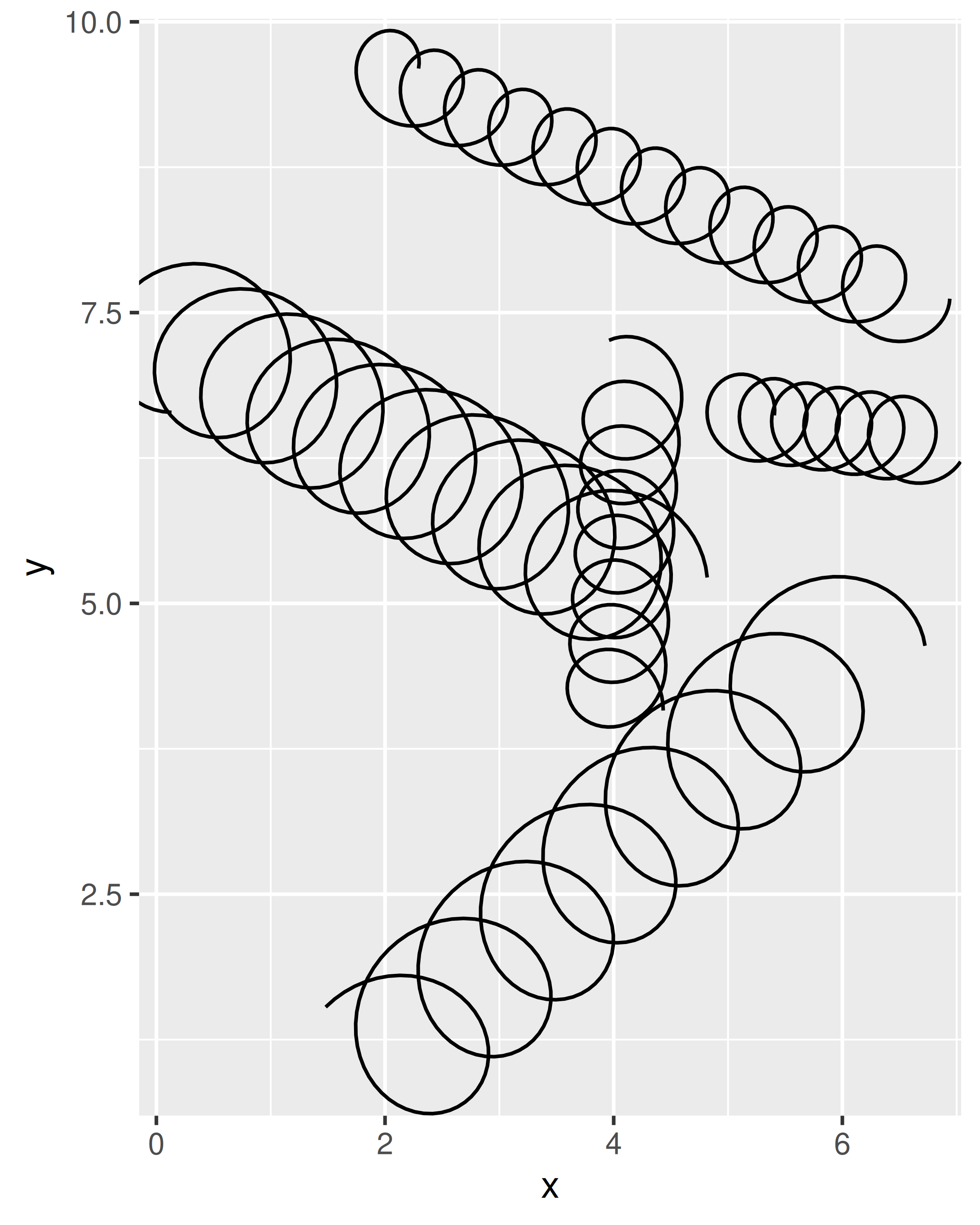

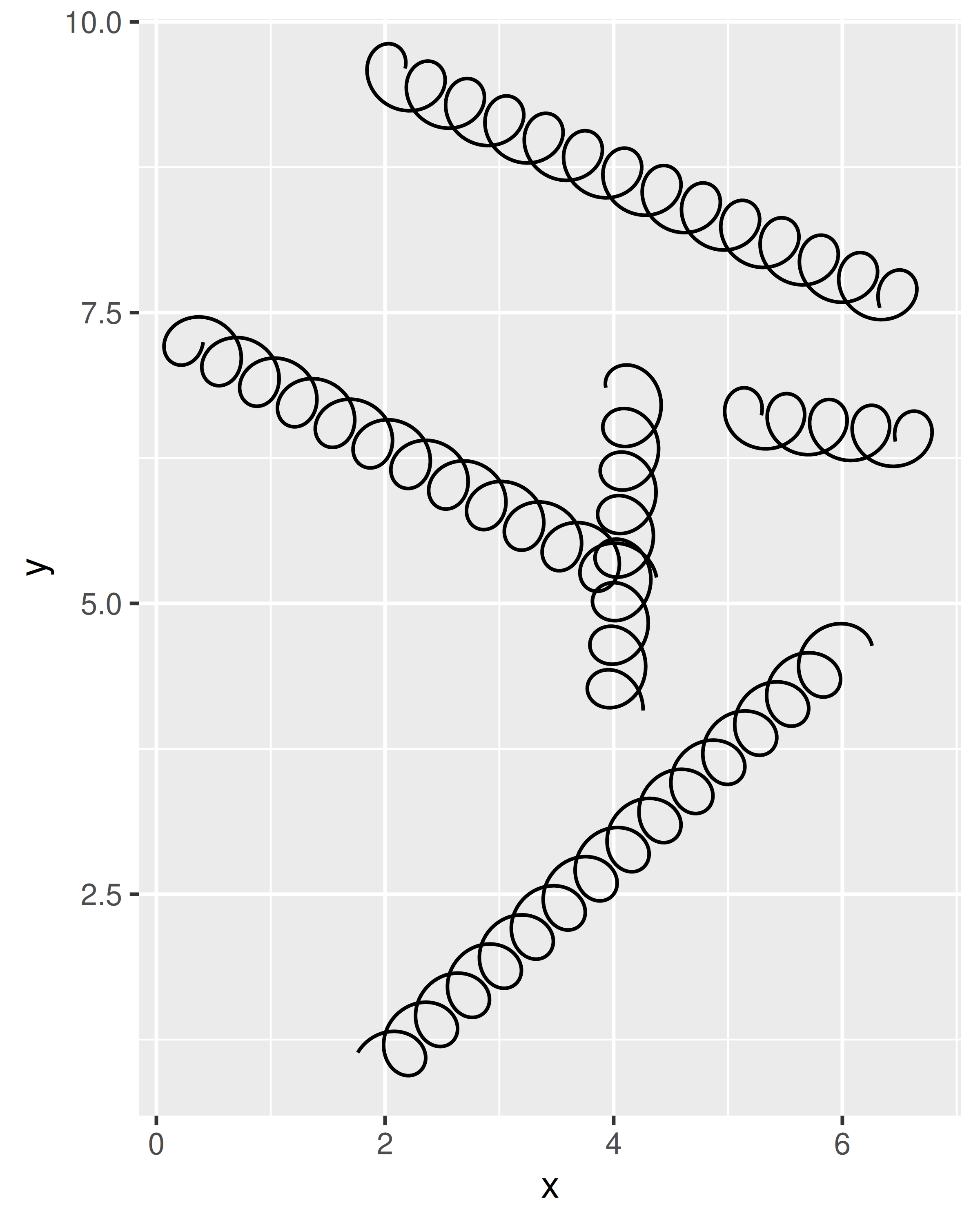
Todavía tiene algunas limitaciones, porque las unidades de diameter y tension se expresan en relación con la escala de los datos sin procesar. El diámetro real de un resorte con diameter = 0.5 será diferente dependiendo de los límites del eje, y si los ejes x e y no están en la misma escala, la forma del resorte se distorsionará. Puedes ver esto en el siguiente ejemplo:

ggplot() + 
  geom_spring(aes(x = 0, y = 0, xend = 3, yend = 20))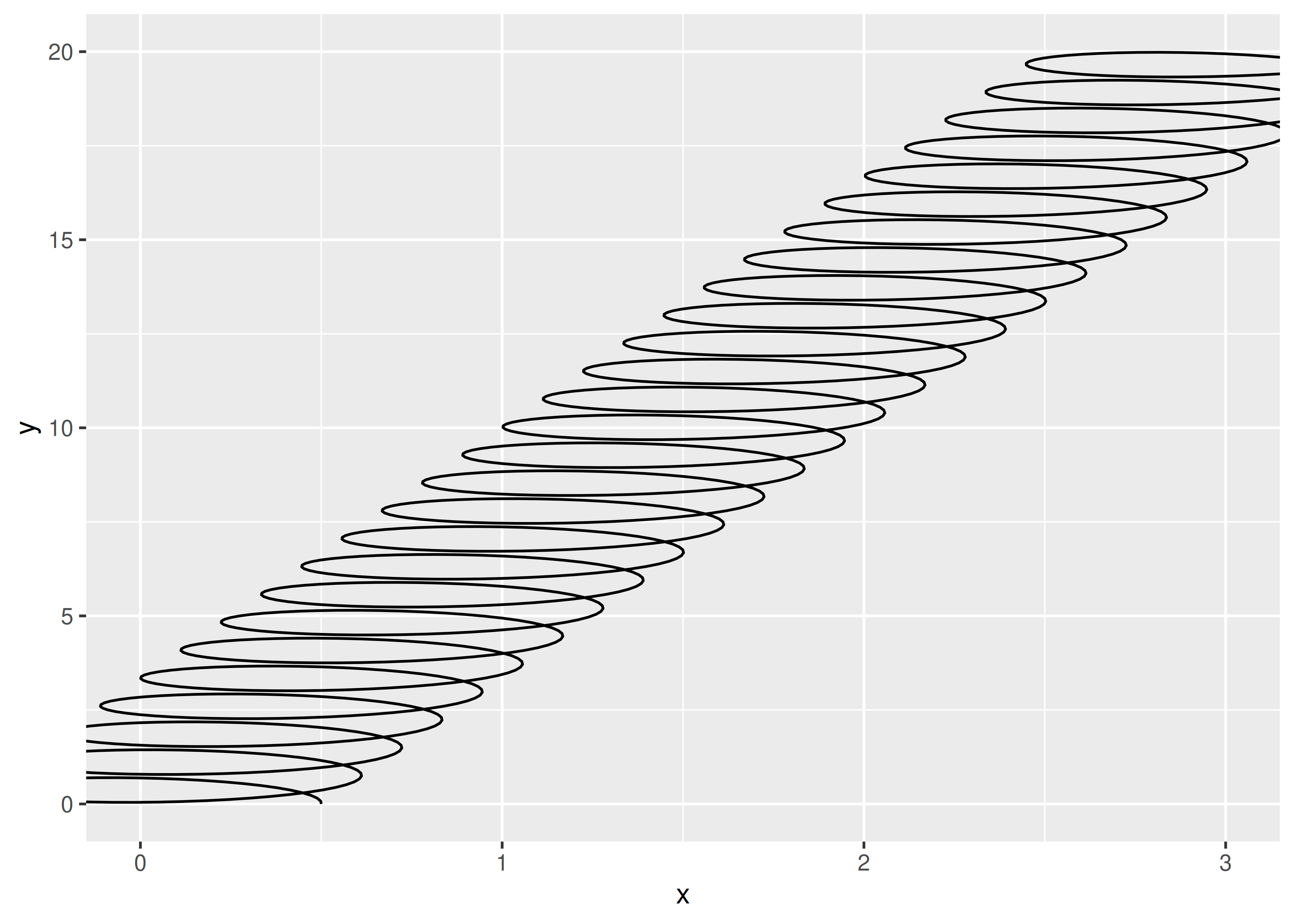

El mismo problema subyacente significa que el diámetro del resorte se expresa en el espacio de coordenadas. Esto hace que sea difícil definir un valor predeterminado significativo porque el tamaño absoluto del diámetro del resorte cambia cuando cambia la escala de los datos:

ggplot() + 
  geom_spring(aes(x = 0, y = 0, xend = 100, yend = 80))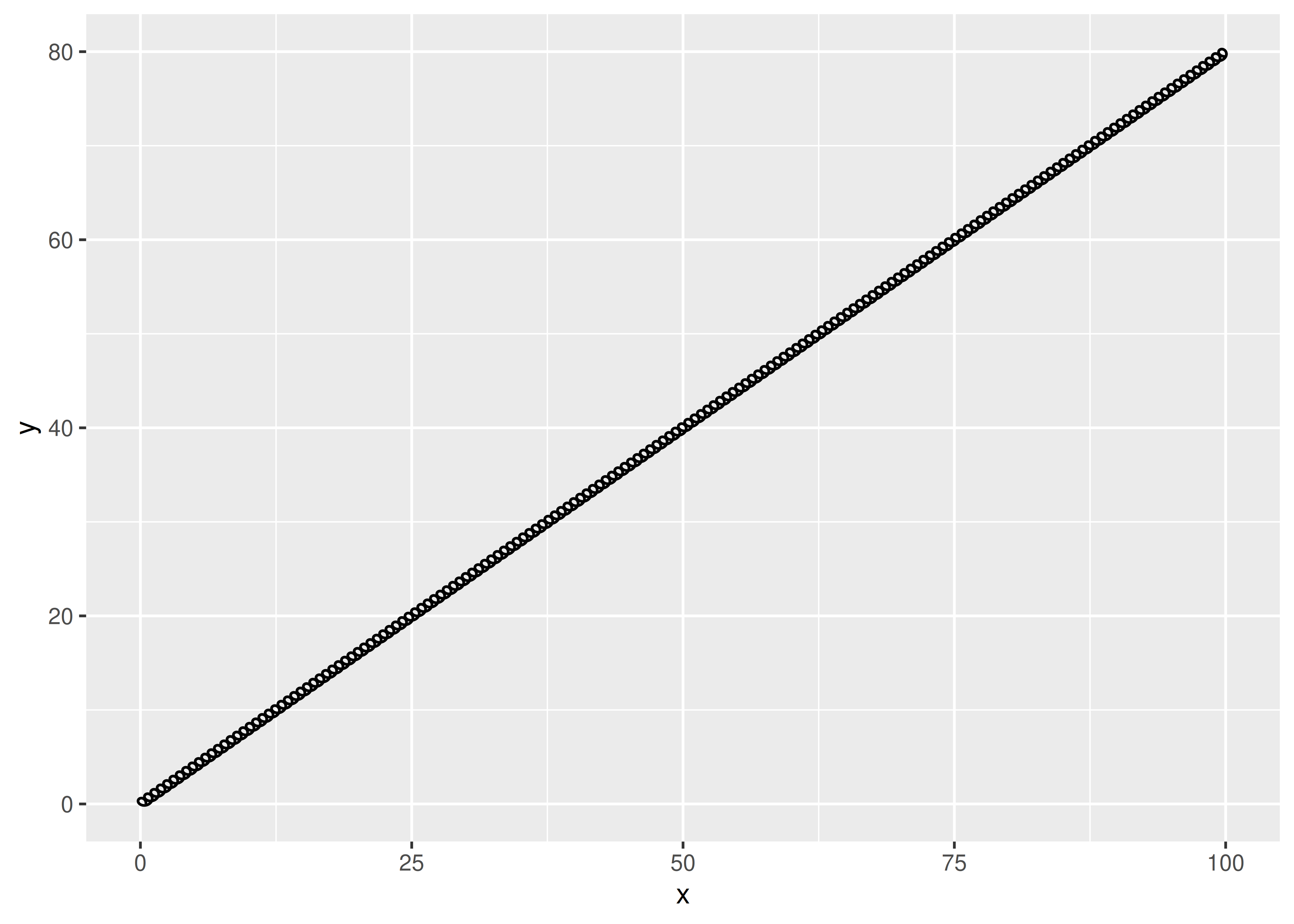

Abordaremos este problema en Sección 21.6.

21.4.5 Post mortem

En esta sección finalmente creamos nuestra propia extensión Geom. Esta suele ser la conclusión natural del desarrollo de una nueva capa, pero no siempre. A veces encontrarás que el enfoque Stat funciona perfectamente para tus propósitos y tiene la ventaja de que puedes usar la estadística con múltiples geoms. La elección final depende de usted como desarrollador y debe guiarse por cómo espera que la gente use la capa.

Quizás sea sorprendente que aún no hayamos hablado sobre lo que sucede dentro de los métodos draw_*(). Nuestro objeto GeomSpring se basa en el método draw_panel() de GeomPath para realizar el trabajo de crear la salida gráfica. Esto es bastante común. Por ejemplo, incluso el relativamente complejo GeomBoxplot simplemente usa los métodos de dibujo de GeomPoint(), GeomSegment y GeomCrossbar.

Si necesita profundizar más, necesitará aprender un poco sobre la cuadrícula. La creación de grid grobs es una técnica avanzada, necesaria para relativamente pocas geoms. Pero crear un grob de cuadrícula le brinda el poder de usar unidades absolutas para el diámetro (por ejemplo, 1 cm) y ajustar la visualización del geom según el tamaño del dispositivo de salida. Nos ocuparemos de eso a continuación.

21.5 Una introducción a la cuadrícula

El paquete grid proporciona el sistema de gráficos subyacente sobre el que se construye ggplot2. Es uno de los dos sistemas de dibujo bastante diferentes que se incluyen en base R: gráficos base y cuadrícula. Los gráficos básicos tienen un modelo imperativo de “lápiz sobre papel”: cada función dibuja inmediatamente algo en el dispositivo gráfico. Al igual que el propio ggplot2, grid adopta un enfoque más declarativo en el que se construye una descripción del gráfico como un objeto, que luego se representa. Este enfoque declarativo nos permite crear objetos que existen independientemente del dispositivo gráfico y que pueden transmitirse, analizarse y modificarse. Es importante destacar que partes de un objeto gráfico pueden hacer referencia a otras partes, lo que le permite hacer cosas como definir este rectángulo para que tenga un ancho igual a la longitud de esa cadena de texto, etc.

Como desarrollador de ggplot2, descubrirá que puede lograr mucho sin necesidad de interactuar directamente con la cuadrícula, pero hay situaciones en las que es imposible lograr lo que desea sin bajar al nivel de la cuadrícula. Las dos situaciones más comunes son:

  1. Necesita crear objetos gráficos que estén ubicados correctamente en el sistema de coordenadas, pero donde alguna parte de su apariencia tenga un tamaño absoluto fijo. En nuestro caso, este sería el resorte yendo correctamente entre dos puntos en el gráfico, pero el diámetro definido en cm en lugar de en relación con el sistema de coordenadas.

  2. Necesita objetos gráficos que se actualicen durante el cambio de tamaño. Esto podría, por ejemplo. ser la posición de etiquetas como en el paquete ggrepel o los geoms geom_mark_*() en ggforce.

Una introducción completa a grid es mucho más de lo que podemos cubrir en este libro, pero para ayudarlo a comenzar, le brindaremos el vocabulario mínimo absoluto para comprender cómo ggplot2 usa grid. Presentaremos conceptos básicos como grobs, ventanas gráficas, parámetros gráficos y unidades, pero lea R Graphics de Murrell (2018) para obtener todos los detalles.

21.5.1 Grobs

Para entender cómo funciona grid, lo primero que debemos hablar son grobs. Grobs (objetosgr**aficos) son representaciones atómicas de elementos gráficos en una cuadrícula e incluyen tipos como puntos, líneas, círculos, rectángulos y texto. El paquete grid proporciona funciones como pointsGrob(), linesGrob(), circleGrob(), rectGrob() y textGrob() que crean objetos gráficos sin dibujar nada en el dispositivo gráfico. Estas funciones están vectorizadas, lo que permite que un solo punto represente múltiples puntos, por ejemplo:

library(grid)
circles <- circleGrob(
  x = c(0.1, 0.4, 0.7), 
  y = c(0.5, 0.3, 0.6),
  r = c(0.1, 0.2, 0.3)
)
circles
#> circle[GRID.circle.582]

Tenga en cuenta que este código no dibuja nada: es sólo una descripción de un conjunto de círculos. Para dibujarlo, primero llamamos a grid.newpage() para borrar el dispositivo gráfico actual y luego grid.draw():

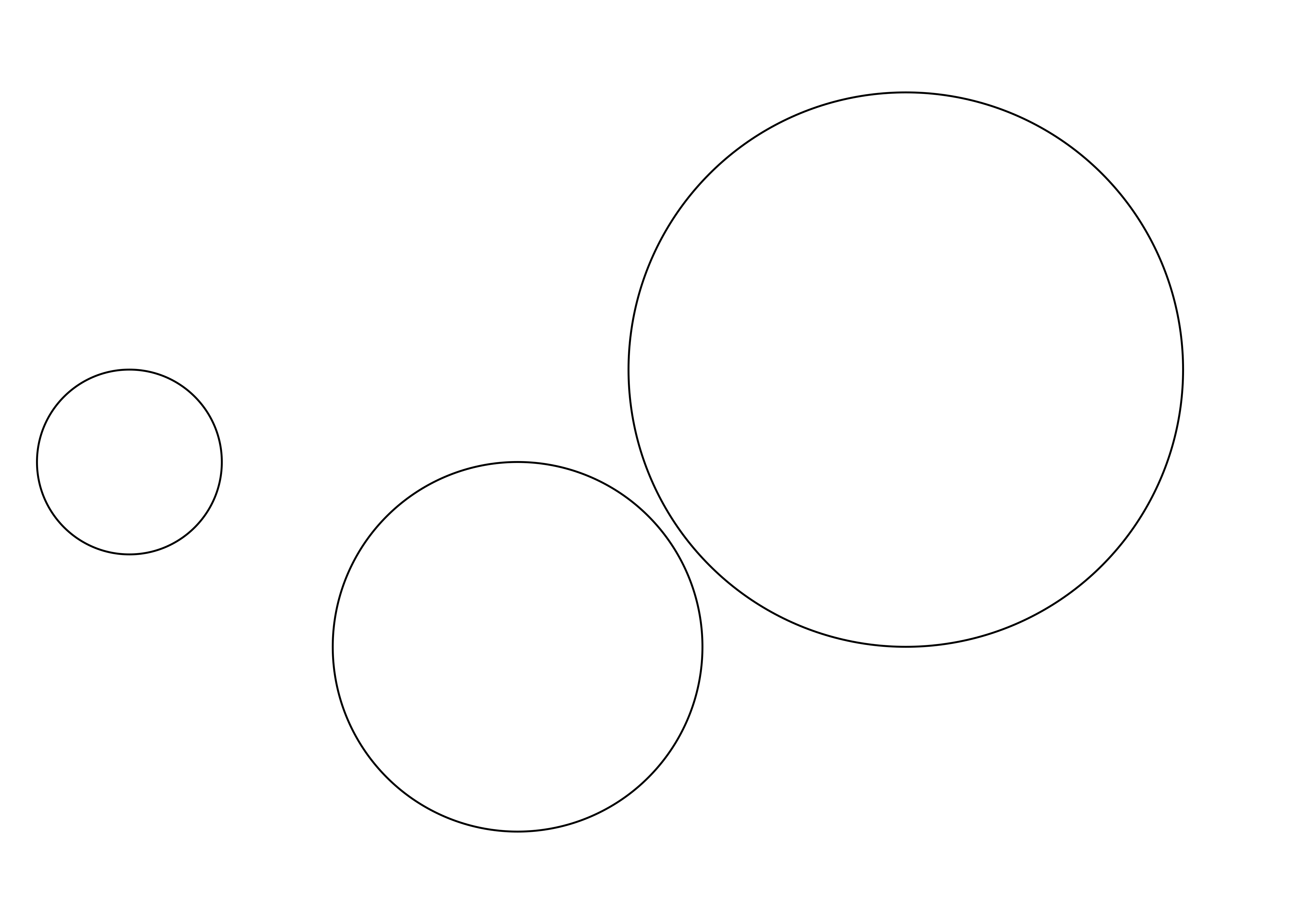
grid también proporciona grobTree(), que construye objetos compuestos a partir de múltiples grobs atómicos. Aquí hay una ilustración:

labels <- textGrob(
  label = c("small", "medium", "large"),
  x = c(0.1, 0.4, 0.7), 
  y = c(0.5, 0.3, 0.6),
)

composite <- grobTree(circles, labels)
grid.newpage()
grid.draw(composite)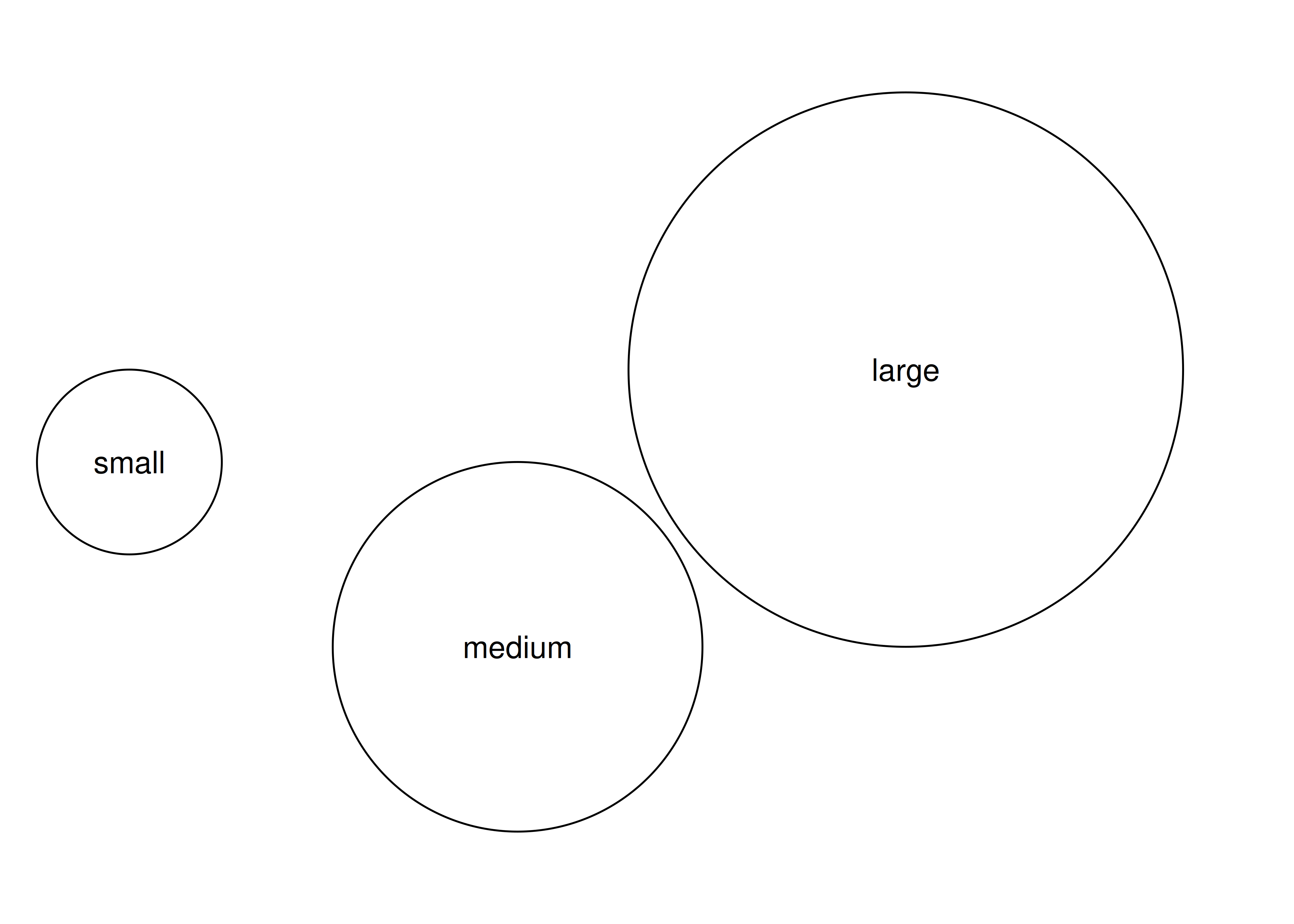

También es posible definir sus propios grobs. Puede definir una nueva clase grob primitiva usando grob() o una nueva clase compuesta usando gTree(), luego especificar un comportamiento especial para su nueva clase. Veremos un ejemplo de esto en un momento.

21.5.2 Ventanas gráficas

El segundo concepto clave en grid es la idea de una ventana gráfica. Una ventana gráfica es una región de trazado rectangular que proporciona su propio sistema de coordenadas para los objetos que se dibujan dentro de ella y también puede proporcionar una cuadrícula tabular en la que se pueden anidar otras ventanas gráficas. Un grob individual puede tener su propia ventana gráfica o, si no se proporciona ninguna, heredará una. Si bien no necesitaremos considerar las ventanas gráficas al construir el grob para nuestros resortes, son un concepto importante que impulsa gran parte del diseño de alto nivel de los gráficos ggplot2, por lo que los presentaremos aquí muy brevemente. En el siguiente ejemplo usamos viewport() para definir dos ventanas gráficas diferentes, una con parámetros predeterminados y la segunda que gira alrededor del punto medio 15 grados:

vp_default <- viewport()
vp_rotated <- viewport(angle = 15)

Esta vez, cuando creemos nuestros grobs compuestos, los asignaremos explícitamente a ventanas gráficas específicas estableciendo el argumento vp:

composite_default <- grobTree(circles, labels, vp = vp_default)
composite_rotated <- grobTree(circles, labels, vp = vp_rotated)

Cuando trazamos estos dos grobs, podemos ver el efecto de la ventana gráfica: aunque composite_default y composite_rotated se componen de los mismos dos grobs primitivos (es decir, circles y labels), pertenecen a ventanas gráficas diferentes, por lo que se ven diferentes cuando se dibuja la gráfica:

grid.newpage()
grid.draw(composite_default)
grid.draw(composite_rotated)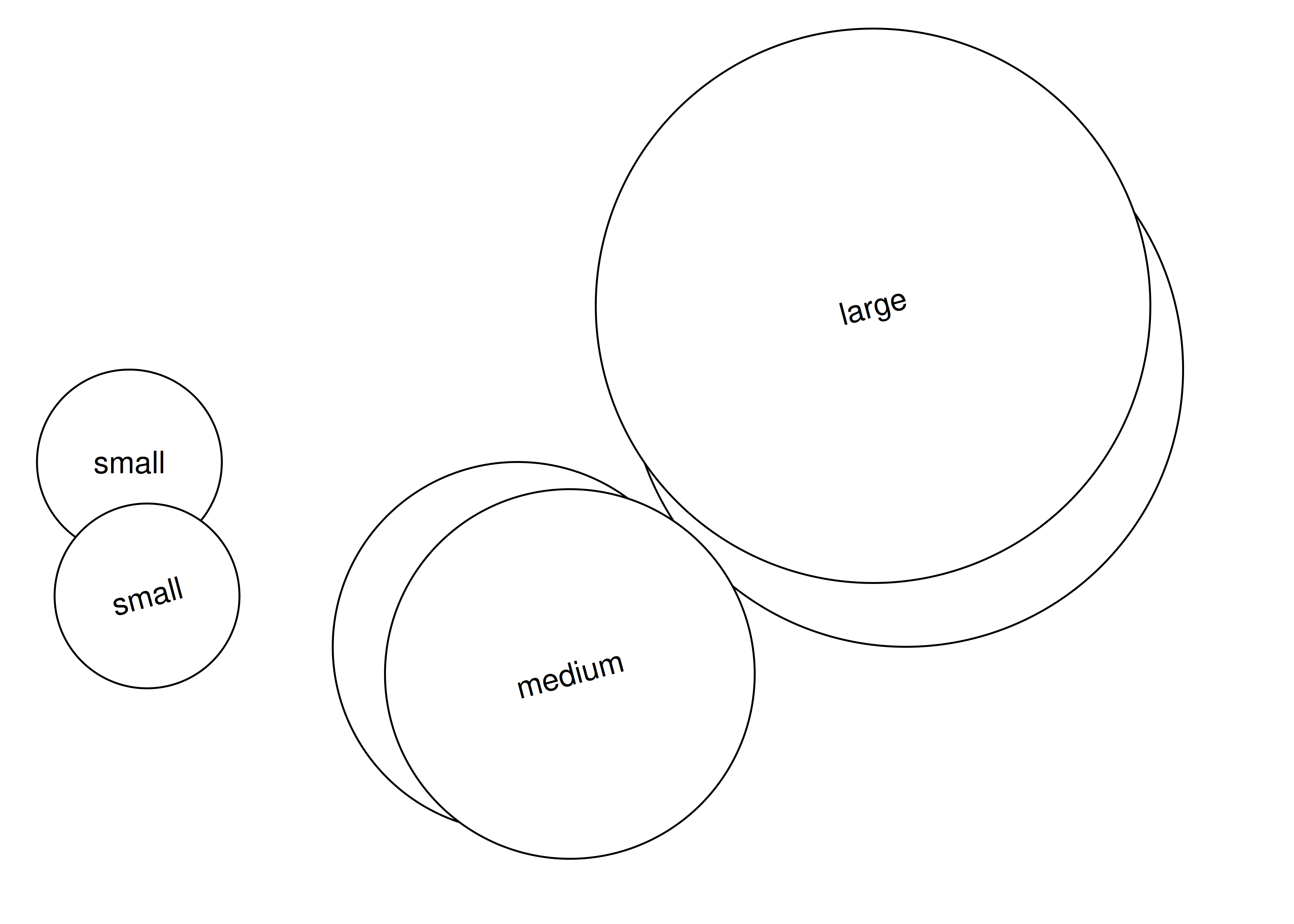

ggplot2 genera automáticamente la mayoría de las ventanas gráficas que necesitará para trazar, pero es importante comprender la idea básica.

21.5.3 Parámetros gráficos

El siguiente concepto que debemos comprender es la idea de parámetros gráficos. Cuando definimos los grobs circles y labels, solo especificamos algunas de sus propiedades. Por ejemplo, no dijimos nada sobre el color o la transparencia, por lo que todas estas propiedades están configuradas en sus valores predeterminados. La función gpar() en grid le permite especificar parámetros gráficos como objetos distintos:

gp_blue <- gpar(col = "blue", fill = NA)
gp_orange <- gpar(col = "orange", fill = NA)

Los objetos gp_blue y gp_orange proporcionan listas de configuraciones gráficas que ahora se pueden aplicar a cualquier grob que queramos usando el argumento gp:

grob1 <- grobTree(circles, labels, vp = vp_default, gp = gp_blue)
grob2 <- grobTree(circles, labels, vp = vp_rotated, gp = gp_orange)

Cuando trazamos estos dos grobs, heredan la configuración proporcionada por los parámetros gráficos así como las ventanas gráficas a las que están asignados:

21.5.4 Unidades

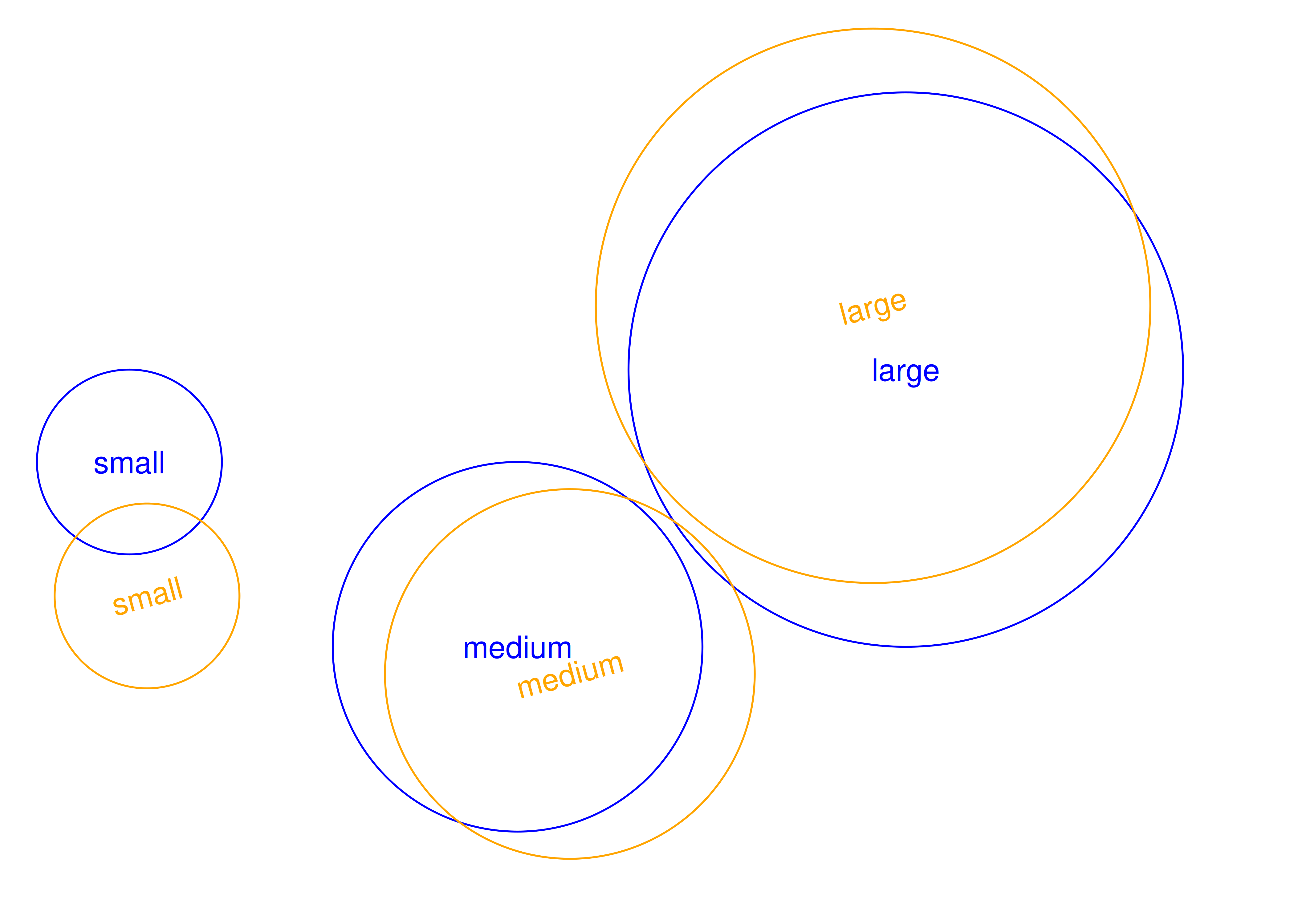
El último concepto central que debemos discutir es el sistema de unidades. El paquete grid le permite especificar las posiciones (por ejemplo, x e y) y las dimensiones (por ejemplo, length y width) de grobs y ventanas gráficas utilizando una especificación flexible. En el sistema de unidades de cuadrícula existen tres estilos de unidades cualitativamente diferentes:

  • Unidades absolutas, p.e. centímetros, pulgadas y puntos se refieren a tamaños físicos.
  • Unidades relativas, p. npc que representa una proporción del tamaño de la ventana gráfica actual.
  • Unidades definidas por cadenas u otros grobs, p.e. strwidth, grobwidth.

La función unit() es la función principal que utilizamos al especificar unidades: unit(1, "cm") es 1 centímetro, mientras que unit(0.5, "npc") es la mitad del tamaño de la ventana gráfica correspondiente. . El sistema de unidades admite operaciones aritméticas que sólo se resuelven en el momento del sorteo, lo que permite combinar diferentes tipos de unidades: unidad(0.5, "npc") + unidad(1, "cm") define un punto a un centímetro de a la derecha del centro de la ventana gráfica actual.

21.5.5 Construyendo clases grob

Ahora que tenemos una comprensión básica de la cuadrícula, intentemos crear nuestra propia clase grob “sorpresa”: objetos que son círculos si miden menos de 3 cm, pero se transforman en cuadrados cuando miden más de 3 cm. Este no es el tipo de objeto gráfico más útil, pero es útil para ilustrar la flexibilidad del sistema de cuadrícula. El primer paso es escribir nuestra propia función constructora usando grob() o gTree(), dependiendo de si estamos creando un objeto primitivo o compuesto. Comenzamos creando una función constructora “delgada”:

surpriseGrob <- function(x, 
                         y, 
                         size, 
                         default.units = "npc", 
                         name = NULL, 
                         gp = gpar(), 
                         vp = NULL) {
  
  # Asegúrese de que los argumentos de entrada sean unidades
  if (!is.unit(x)) x <- unit(x, default.units)
  if (!is.unit(y)) y <- unit(y, default.units)
  if (!is.unit(size)) size <- unit(size, default.units)
  
  # Construya la subclase grob sorpresa como un gTree
  gTree(
    x = x, 
    y = y, 
    size = size, 
    name = name, 
    gp = gp, 
    vp = vp, 
    cl = "surprise"
  )
}

Esta función no hace mucho. Todo lo que hace es garantizar que los argumentos x, y y size sean unidades de cuadrícula y establece que el nombre de la clase sea “sorpresa”. Para definir el comportamiento de nuestro grob, necesitamos especificar métodos para una o ambas funciones genéricas makeContext() y makeContent():

  • makeContext() se llama cuando se representa el grob principal y le permite controlar la ventana gráfica del grob. No necesitaremos usar eso para nuestra sorpresa.

  • makeContent() se llama cada vez que se cambia el tamaño de la región de dibujo y le permite personalizar el aspecto del grob según el tamaño u otro aspecto.

Debido a que estas funciones genéricas utilizan el sistema de programación orientada a objetos S3, podemos definir nuestro método simplemente agregando el nombre de la clase al final del nombre de la función. Es decir, el método makeContent() para nuestro grob sorpresa se define creando una función llamada makeContent.surprise() que toma un grob como entrada y devuelve un grob modificado como salida:

makeContent.surprise <- function(x) {
  x_pos <- x$x
  y_pos <- x$y
  size <- convertWidth(x$size, unitTo = "cm", valueOnly = TRUE)
  
  # Averigua si los tamaños dados son mayores o menores de 3 cm.
  circles <- size < 3
  
  # Crea un círculo para los más pequeños.
  if (any(circles)) {
    circle_grob <- circleGrob(
      x = x_pos[circles], 
      y = y_pos[circles], 
      r = unit(size[circles] / 2, "cm")
    )
  } else {
    circle_grob <- NULL
  }
  
  # Crea un grob recto para los grandes.
  if (any(!circles)) {
    square_grob <- rectGrob(
      x = x_pos[!circles], 
      y = y_pos[!circles], 
      width = unit(size[!circles], "cm"),
      height = unit(size[!circles], "cm")
    )
  } else {
    square_grob <- NULL
  }
  
  # Agregue el círculo y rectifique grob como hijos de nuestro grob de entrada
  setChildren(x, gList(circle_grob, square_grob))
}

Algunas de las funciones que hemos llamado aquí son nuevas, pero todas reutilizan los conceptos centrales que analizamos anteriormente. Específicamente:

  • convertWidth() se utiliza para convertir unidades de cuadrícula de un tipo a otro.
  • gList() crea una lista de grobs.
  • setChildren() especifica los grobs que pertenecen a un grob compuesto de gTree.

El efecto de esta función es garantizar que cada vez que se renderiza el grob se recalcule el tamaño absoluto de cada forma. Todas las formas menores de 3 cm se convierten en círculos y todas las formas mayores de 3 cm se convierten en cuadrados. Para ver cómo se desarrolla esto, llamemos a nuestra nueva función:

surprises <- surpriseGrob(
  x = c(0.25, 0.45, 0.75), 
  y = c(0.5, 0.5, 0.5), 
  size = c(0.05, 0.15, 0.25)
)

El grob surprises contiene tres formas cuyas ubicaciones y tamaños se han especificado en relación con el tamaño de la ventana gráfica. En este momento no tenemos idea de cuáles de estas formas serán círculos y cuáles serán cuadrados: eso depende del tamaño de la ventana gráfica en la que se dibujará el grob surprises. Ahora podemos dibujar el grob de la forma habitual:

grid.newpage()
grid.draw(surprises)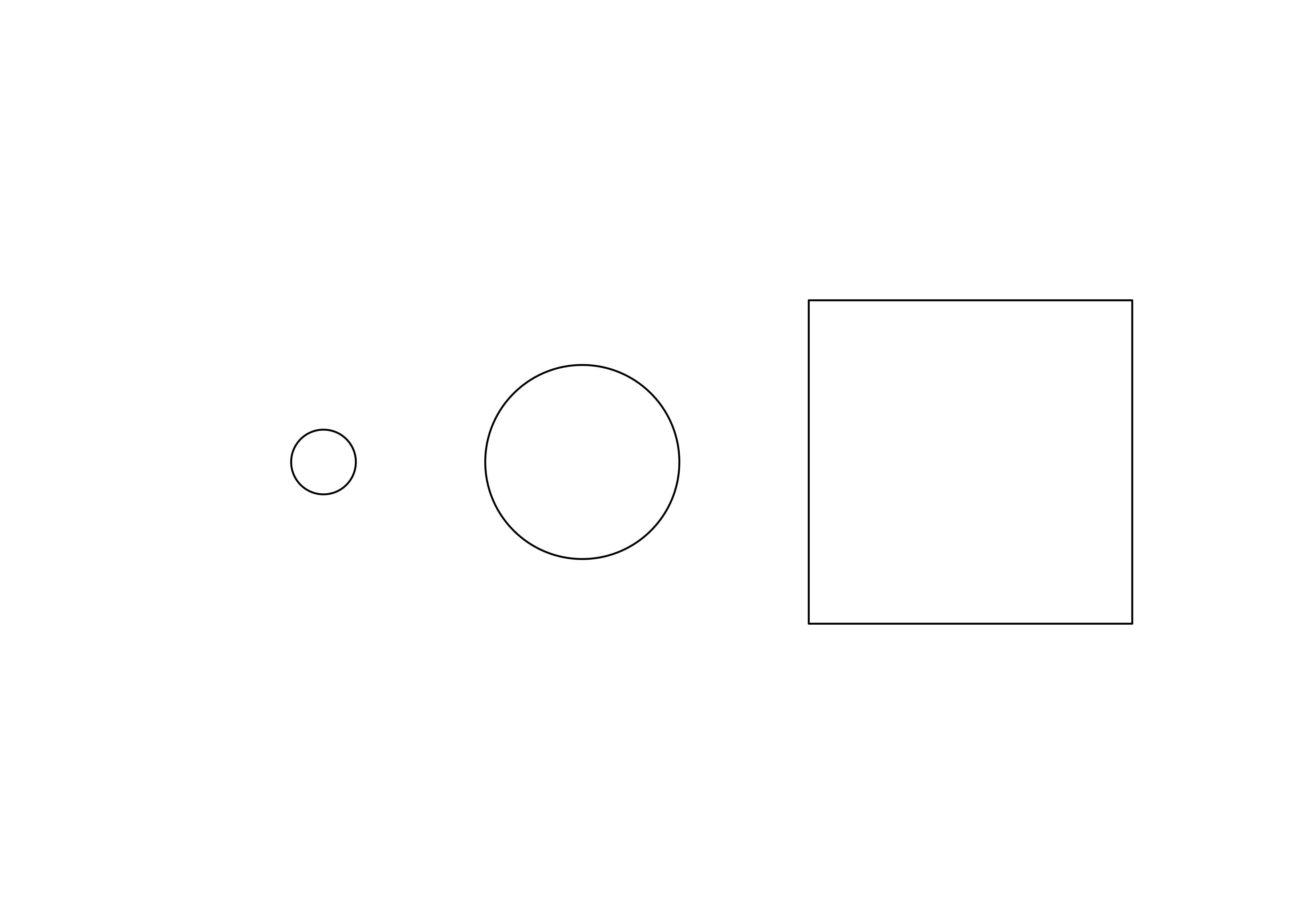

Si ejecuta este código de forma interactiva y cambia el tamaño de la ventana de trazado, verá que los tres objetos cambian de forma según el tamaño de la ventana de trazado. Esta no es la forma más útil de emplear grid, por supuesto, pero esperamos que puedas ver cómo se puede utilizar esta técnica para realizar un trabajo real.

21.5.6 Cuadrícula tabular

El último aspecto de grid que discutiremos aquí es el motor de diseño proporcionado por el paquete gtable. No es necesario saber acerca de gtable para construir nuestro spring grob, pero hay otros tipos de extensiones ggplot2 que sí requieren este conocimiento, por lo que brindaremos una breve descripción aquí.

Como se discutió en Sección 19.3, cuando ggplot2 pasa el gráfico a la cuadrícula para renderizarlo, lo hace creando un objeto gtable con ggplot_gtable(). Podemos extraer este objeto usando la función ggplotGrob():

p <- ggplot(mpg, aes(displ, hwy)) + geom_point()
grob_table <- ggplotGrob(p)
grob_table
#> TableGrob (16 x 13) "layout": 22 grobs
#>     z         cells             name
#> 1   0 ( 1-16, 1-13)       background
#> 2   5 ( 8- 8, 6- 6)           spacer
#> 3   7 ( 9- 9, 6- 6)           axis-l
#> 4   3 (10-10, 6- 6)           spacer
#> 5   6 ( 8- 8, 7- 7)           axis-t
#> 6   1 ( 9- 9, 7- 7)            panel
#> 7   9 (10-10, 7- 7)           axis-b
#> 8   4 ( 8- 8, 8- 8)           spacer
#> 9   8 ( 9- 9, 8- 8)           axis-r
#> 10  2 (10-10, 8- 8)           spacer
#> 11 10 ( 7- 7, 7- 7)           xlab-t
#> 12 11 (11-11, 7- 7)           xlab-b
#> 13 12 ( 9- 9, 5- 5)           ylab-l
#> 14 13 ( 9- 9, 9- 9)           ylab-r
#> 15 14 ( 9- 9,11-11)  guide-box-right
#> 16 15 ( 9- 9, 3- 3)   guide-box-left
#> 17 16 (13-13, 7- 7) guide-box-bottom
#> 18 17 ( 5- 5, 7- 7)    guide-box-top
#> 19 18 ( 9- 9, 7- 7) guide-box-inside
#> 20 19 ( 4- 4, 7- 7)         subtitle
#> 21 20 ( 3- 3, 7- 7)            title
#> 22 21 (14-14, 7- 7)          caption
#>                                             grob
#> 1                rect[plot.background..rect.629]
#> 2                                 zeroGrob[NULL]
#> 3            absoluteGrob[GRID.absoluteGrob.618]
#> 4                                 zeroGrob[NULL]
#> 5                                 zeroGrob[NULL]
#> 6                       gTree[panel-1.gTree.610]
#> 7            absoluteGrob[GRID.absoluteGrob.614]
#> 8                                 zeroGrob[NULL]
#> 9                                 zeroGrob[NULL]
#> 10                                zeroGrob[NULL]
#> 11                                zeroGrob[NULL]
#> 12 titleGrob[axis.title.x.bottom..titleGrob.621]
#> 13   titleGrob[axis.title.y.left..titleGrob.624]
#> 14                                zeroGrob[NULL]
#> 15                                zeroGrob[NULL]
#> 16                                zeroGrob[NULL]
#> 17                                zeroGrob[NULL]
#> 18                                zeroGrob[NULL]
#> 19                                zeroGrob[NULL]
#> 20         zeroGrob[plot.subtitle..zeroGrob.626]
#> 21            zeroGrob[plot.title..zeroGrob.625]
#> 22          zeroGrob[plot.caption..zeroGrob.627]

El resultado ilustra cómo está estructurado el diseño de ggplot2. La gráfica se compone de 18 grobs distintos que están organizados en un TableGrob que especifica una cuadrícula de 12 x 9, que a su vez proporciona una colección de ventanas gráficas dentro de las cuales se pueden dibujar grobs individuales. Este TableGrob es en sí mismo un grobtree y se puede representar con grid llamando grid.draw():

grid.newpage()
grid.draw(grob_table)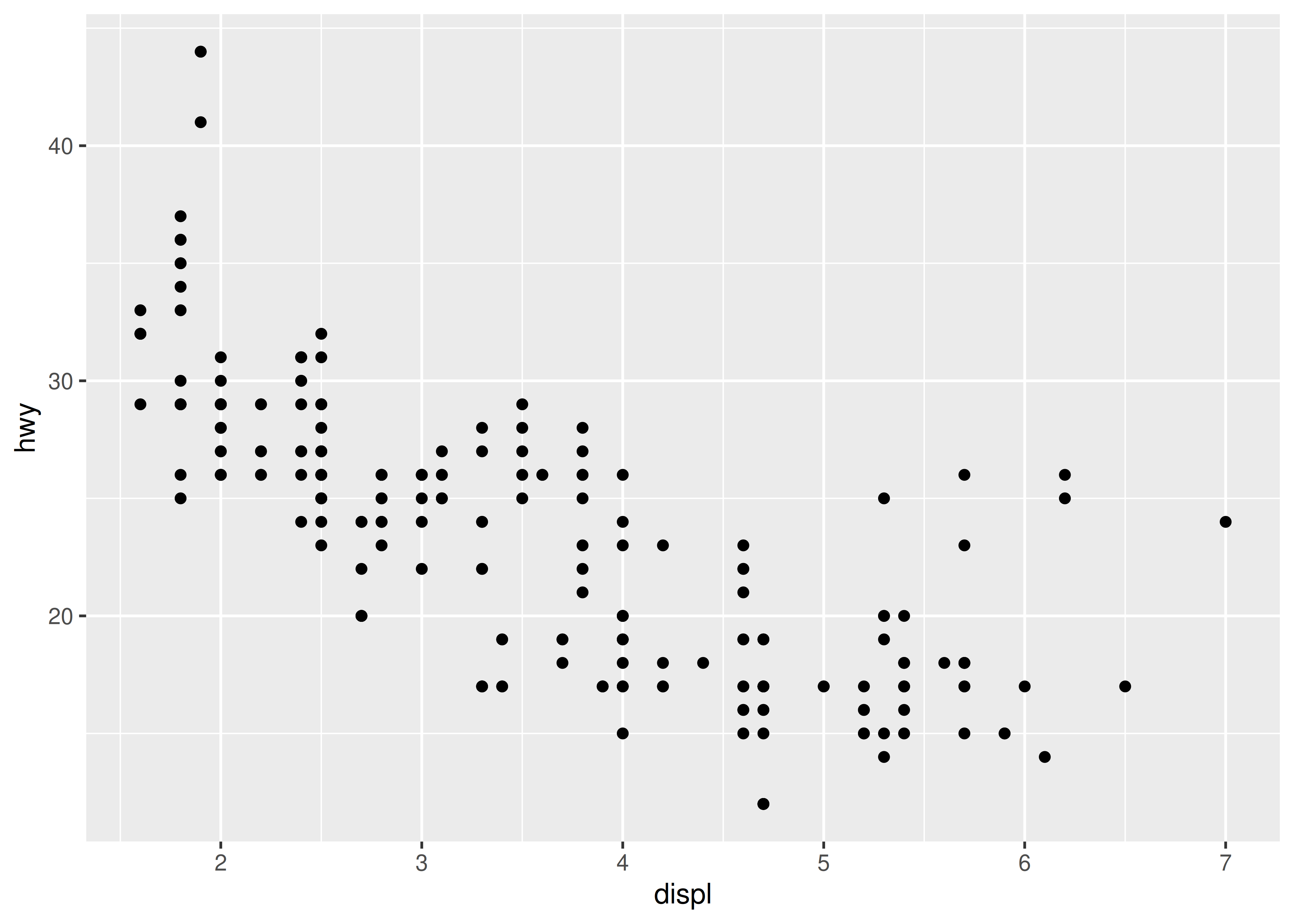

Para ilustrar cómo funciona TableGrob, crearemos una versión simplificada de este resultado sin usar ggplot2. Nuestro primer paso es definir los grobs constituyentes que componen nuestra gráfica:

xtick <- 0:8
ytick <- seq(0, 50, 10)

points <- pointsGrob(
  x = mpg$displ / xtick[length(xtick)],
  y = mpg$hwy / ytick[length(ytick)],
  default.units = 'npc',
  size = unit(6, 'pt')
)

xaxis <- xaxisGrob(
  at = seq(0, 1, length.out = length(xtick)), 
  label = xtick
)

yaxis <- yaxisGrob(
  at = seq(0, 1, length.out = length(ytick)), 
  label = ytick
)

El grob points contiene los datos que se van a trazar, mientras que xaxis y yaxis son grobs que dibujan ejes etiquetados. Cuando dibujamos el grob de points, obtenemos el núcleo de un diagrama de dispersión:

Sin embargo, si queremos agregar ejes a este gráfico, necesitamos un conjunto de ventanas gráficas dispuestas en formato tabular para que podamos colocar el xaxis inmediatamente debajo de los points y el yaxis a la izquierda de los points. En ggplot2, esto lo maneja el motor de diseño gtable. Primero, usamos gtable() para definir la estructura:

library(gtable)

plot_layout <- gtable(
  widths = unit(c(1.5, 0, 1, 0.5), c('cm', 'cm', 'null', 'cm')),
  heights = unit(c(0.5, 1, 0, 1.5), c('cm', 'null', 'cm', 'cm'))
)

El objeto plot_layout es un TableGrob de 4 x 4 que define ventanas gráficas con tamaños que coinciden con las alturas de filas y los anchos de columna que pasamos a gtable(). La función gtable_show_layout() proporciona una manera conveniente de visualizar este diseño:

gtable_show_layout(plot_layout)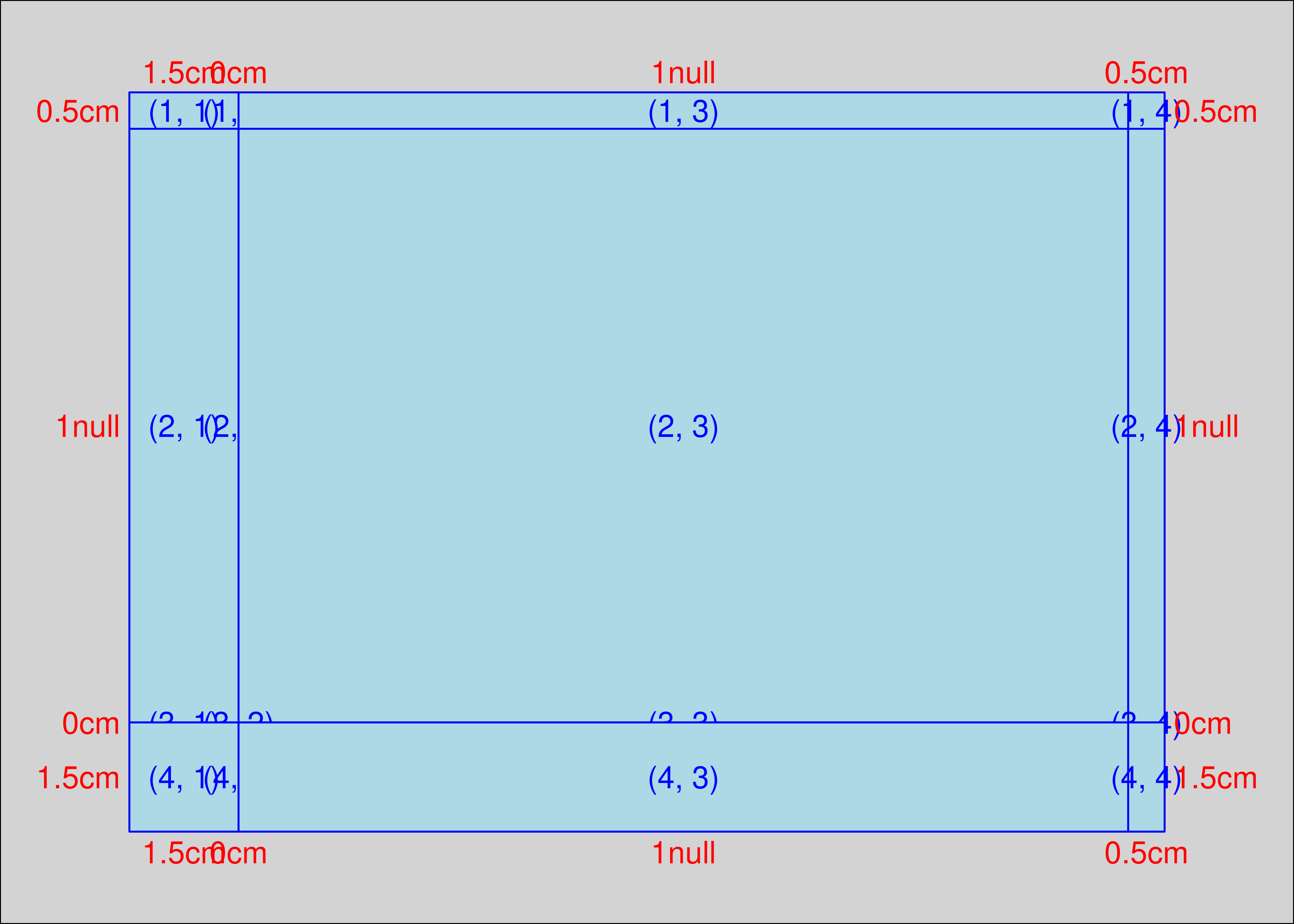

Observe que este diseño tiene una fila con altura cero y una columna con ancho cero. Colocaremos los grobs xaxis y yaxis en estas filas y les permitiremos “desbordarse” en las filas y columnas adyacentes que especifican los márgenes del gráfico.

Para colocar los grobs en la mesa, usamos la función gtable_add_grob(). Un diseño TableGrob permite que un grob individual abarque varias celdas usando los argumentos t, l, b y r para especificar índices de celda para las celdas que están más arriba, más a la izquierda, más al fondo y más a la derecha abarcadas por el grob. Sin embargo, el valor predeterminado es asumir que cada grob pertenece exactamente a una celda, en cuyo caso solo es necesario especificar los argumentos t y l:

plot_layout <- gtable_add_grob(
  plot_layout,
  grobs = list(points, xaxis, yaxis),
  t = c(2, 3, 2), # la fila que define la extensión superior de cada grob
  l = c(3, 3, 2), # la columna que define la extensión izquierda de cada grob
  clip = 'off'
)

Si inspeccionamos nuestro objeto plot_layout, vemos algo que tiene la misma estructura que el TableGrob producido por el código ggplot2 anterior:

plot_layout
#> TableGrob (4 x 4) "layout": 3 grobs
#>   z     cells   name                    grob
#> 1 1 (2-2,3-3) layout points[GRID.points.630]
#> 2 2 (3-3,3-3) layout   xaxis[GRID.xaxis.631]
#> 3 3 (2-2,2-2) layout   yaxis[GRID.yaxis.632]

Ahora podemos dibujar nuestra gráfica usando grid.draw():

grid.newpage()
grid.draw(plot_layout)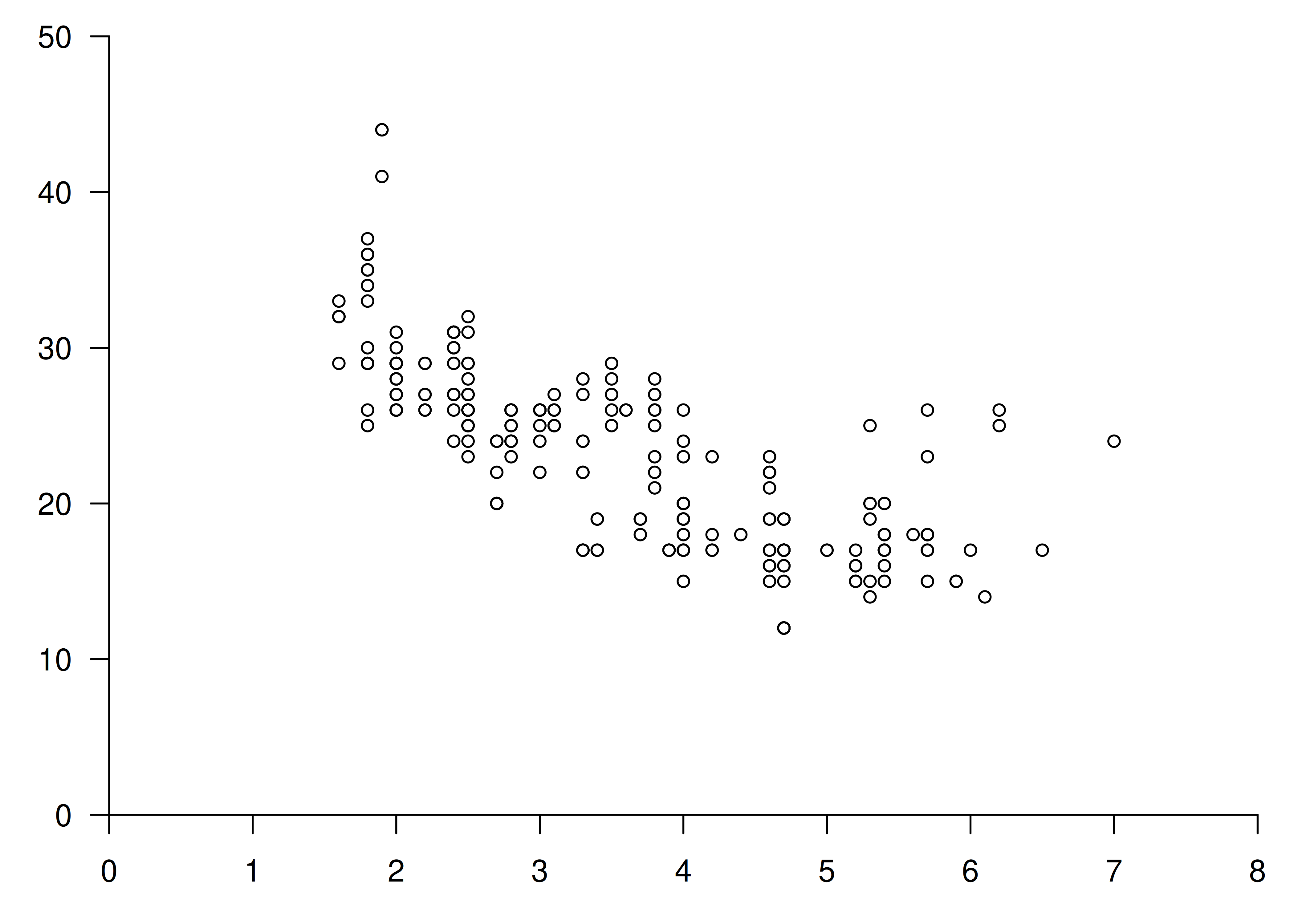

Claramente, todavía nos faltan muchos detalles importantes que serían necesarios en una gráfica real, pero esperamos que ahora esté claro cómo ggplot2 organiza una colección de grobs dentro de un diseño de gráfica estructurado.

21.6 Parte 4: Un grid grob

Volvamos al problema que nos ocupa. Armados con nuestro nuevo conocimiento del sistema de rejilla, podemos construir un resorte que especifique el diámetro en unidades absolutas.

21.6.1 springGrob

Comencemos definiendo la función springGrob(). Nuestra idea clave es que podemos escribir el código grob de una manera que impulse la acción de extracción del resorte hasta el nivel de la función makeContent(). Al hacer esto, podemos asegurarnos de que el diámetro se calcule en el momento del dibujo utilizando unidades absolutas en lugar de definir el diámetro en relación con las coordenadas del trazado.

Comenzaremos creando nuestra función constructora. Los argumentos de esta función se basan en segmentsGrob() ya que, en esencia, estamos dibujando segmentos modificados:

springGrob <- function(x0 = unit(0, "npc"), 
                       y0 = unit(0, "npc"), 
                       x1 = unit(1, "npc"), 
                       y1 = unit(1, "npc"), 
                       diameter = unit(0.1, "npc"), 
                       tension = 0.75,
                       n = 50, 
                       default.units = "npc", 
                       name = NULL, 
                       gp = gpar(), 
                       vp = NULL) {
  
  # Utilice la unidad predeterminada si el usuario no especifica una
  if (!is.unit(x0)) x0 <- unit(x0, default.units)
  if (!is.unit(x1)) x1 <- unit(x1, default.units)
  if (!is.unit(y0)) y0 <- unit(y0, default.units)
  if (!is.unit(y1)) y1 <- unit(y1, default.units)
  if (!is.unit(diameter)) diameter <- unit(diameter, default.units)
  
  # Devuelve un gTree de clase "spring"
  gTree(
    x0 = x0, 
    y0 = y0, 
    x1 = x1, 
    y1 = y1, 
    diameter = diameter, 
    tension = tension, 
    n = n, 
    name = name, 
    gp = gp, 
    vp = vp, 
    cl = "spring"
  )
}

Vemos que una vez más nuestro constructor es una envoltura muy delgada alrededor de gTree(). No introduce ningún concepto nuevo: todo lo que hace es garantizar que los argumentos se conviertan a unidades si es necesario y luego devuelve un grob compuesto con clase “spring”. El trabajo de dibujar nuestro resorte ocurre en el método makeContent():

makeContent.spring <- function(x) {
  
  # Convertir valores de posición y diámetro en unidades absolutas
  x0 <- convertX(x$x0, "mm", valueOnly = TRUE)
  x1 <- convertX(x$x1, "mm", valueOnly = TRUE)
  y0 <- convertY(x$y0, "mm", valueOnly = TRUE)
  y1 <- convertY(x$y1, "mm", valueOnly = TRUE)
  diameter <- convertWidth(x$diameter, "mm", valueOnly = TRUE)
  
  # Deja la tensión y n intacta.
  tension <- x$tension
  n <- x$n
  
  # Transforme los datos de entrada en un marco de datos que contenga rutas de primavera
  springs <- lapply(seq_along(x0), function(i) {
    cbind(
      create_spring(
        x = x0[i], 
        y = y0[i], 
        xend = x1[i], 
        yend = y1[i], 
        diameter = diameter[i], 
        tension = tension[i], 
        n = n
      ),
      id = i
    )
  })
  springs <- do.call(rbind, springs)
  
  # Construir el grob
  spring_paths <- polylineGrob(
    x = springs$x, 
    y = springs$y, 
    id = springs$id, 
    default.units = "mm", 
    gp = x$gp
  )
  setChildren(x, gList(spring_paths))
}

Nuevamente hay un par de nuevas funciones de cuadrícula aquí, pero esperamos que no sea demasiado difícil descubrir qué hacen. La verdad es que aquí no pasa nada especial. Cada vez que se cambia el tamaño del gráfico, tomamos las coordenadas y la configuración del diámetro del resorte y los convertimos todos a milímetros. Sólo después de convertir las cantidades importantes a unidades absolutas construimos las rutas de resorte usando la función create_spring() que escribimos al principio: al llevar la llamada a create_spring() a este nivel, podemos asegurarnos de que la ruta sea definido usando unidades absolutas y luego devuelve el resultado como un grob de polilínea.

Ahora tenemos un spring grob adecuado para usar en ggplot2. En la siguiente sección construiremos una geom a su alrededor, pero antes de hacerlo, verifiquemos que nuestro código se comporte como se esperaba:

springs <- springGrob(
  x0 = c(0, 0),
  y0 = c(0, 0.5),
  x1 = c(1, 1),
  y1 = c(1, 0.5),
  diameter = unit(c(1, 3), "cm"),
  tension = c(0.2, 0.7)
)
grid.newpage()
grid.draw(springs)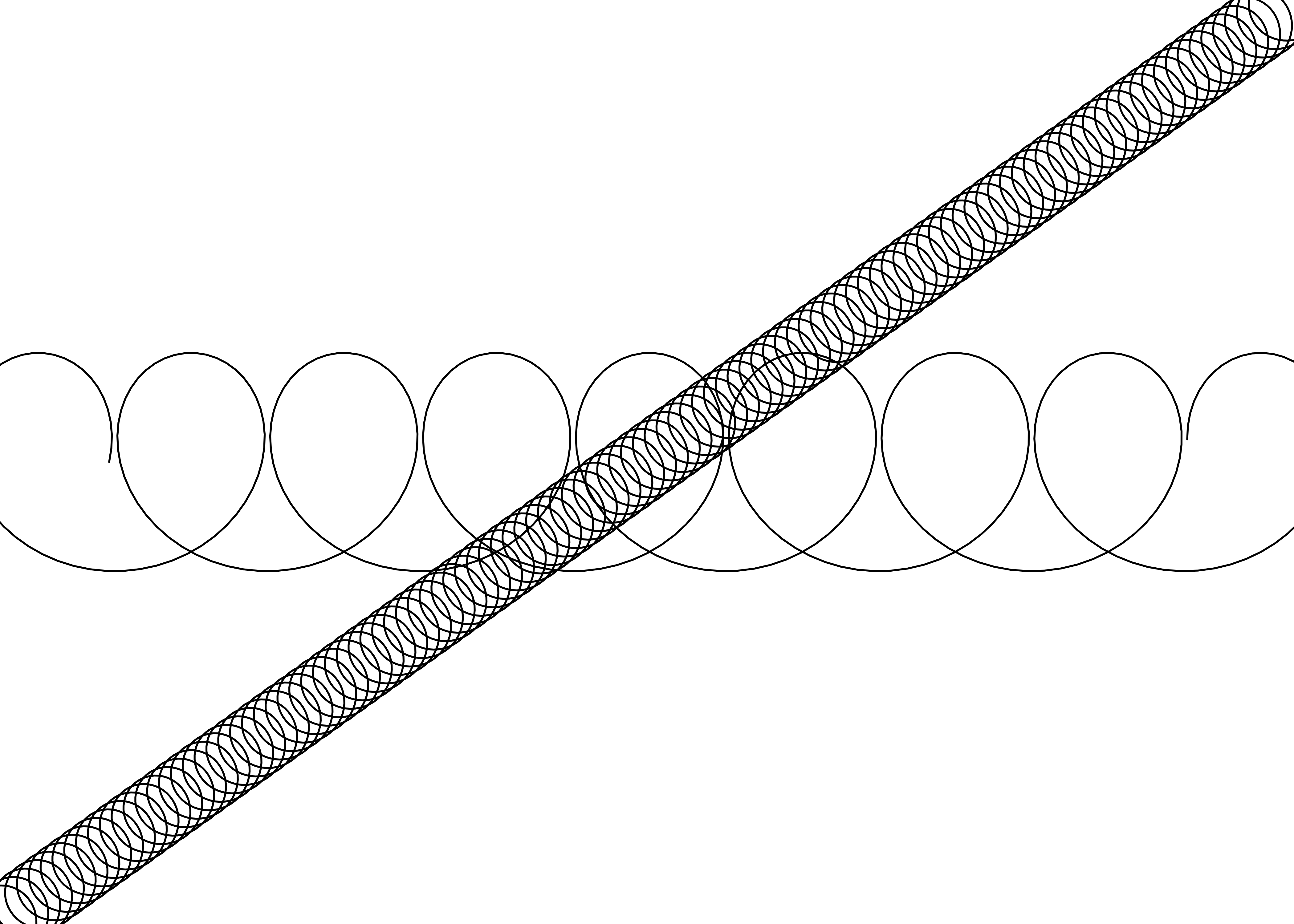

Esto se ve bien, por lo que ahora podemos diseñar nuestra nueva (y final) geom.

21.6.2 El último GeomSpring

Ahora que tenemos un grob personalizado que dibuja resortes, podemos crear un objeto ggproto GeomSpring que lo use. Aquí está el código completo para esa geom:

GeomSpring <- ggproto("GeomSpring", Geom,
  
  # Compruebe que el usuario haya especificado parámetros sensibles                    
  setup_params = function(data, params) {
    if (is.null(params$n)) {
      params$n <- 50
    } else if (params$n <= 0) {
      rlang::abort("Springs must be defined with `n` greater than 0")
    }
    params
  },
  
  # Verifique los datos de entrada y devuelva grobs
  draw_panel = function(data, 
                        panel_params, 
                        coord, 
                        n = 50, 
                        lineend = "butt", 
                        na.rm = FALSE) {
    
    # Elimine los datos faltantes y regrese temprano si faltan todos
    data <- remove_missing(
      df = data, 
      na.rm = na.rm,
      vars = c("x", "y", "xend", "yend", "linetype", "linewidth"),
      name = "geom_spring"
    )
    if (is.null(data) || nrow(data) == 0) return(zeroGrob())
    
    # Proporcionar el sistema de coordenadas para la gráfica.
    if (!coord$is_linear()) {
      rlang::warn(
        "spring geom only works correctly on linear coordinate systems"
      )
    }
    coord <- coord$transform(data, panel_params)
    
    # Construir el grob
    springGrob(
      coord$x, 
      coord$y, 
      coord$xend, 
      coord$yend,
      default.units = "native", 
      diameter = unit(coord$diameter, "cm"),
      tension = coord$tension, 
      n = n,
      gp = gpar(
        col = alpha(coord$colour, coord$alpha),
        lwd = coord$linewidth * .pt,
        lty = coord$linetype,
        lineend = lineend
      )
    )
  },
  
  # Especificar la estética predeterminada y requerida
  required_aes = c("x", "y", "xend", "yend"),
  default_aes = aes(
    colour = "black", 
    linewidth = 0.5, 
    linetype = 1L, 
    alpha = NA, 
    diameter = 0.35, 
    tension = 0.75
  )
)

Hay algunas cosas a tener en cuenta aquí. Como era de esperar, los principales cambios con respecto a la última versión se encuentran en el método draw_panel() (ver más abajo). Pero hay un par de cambios más.

  • Las versiones anteriores de GeomSpring, y StatSpring anteriores, incluían un método setup_data() que modificaba la columna de grupo en los datos de entrada. Eso ya no existe: ya no necesitamos preocuparnos por esto porque esta nueva versión de geom no llama a create_spring() directamente. En lo que respecta a la geom, cada resorte está definido por una (y solo una) fila en los datos de entrada. Todo el trabajo de “expandir” esto a un camino similar a un resorte lo realiza grob.

  • Esta versión de GeomSpring tiene un método setup_params(). Su única función es comprobar el número de puntos utilizados para definir el resorte.

  • El campo default_aes es ligeramente diferente. El cambio importante es que ahora podemos establecer un valor predeterminado significativo para diameter.

Ahora echemos un vistazo más de cerca al nuevo método draw_panel(). Debido a que ya no dependemos de GeomPath$draw_panel() para hacer el trabajo, tenemos algunas tareas nuevas de las que ocuparnos:

  • Comprueba si el sistema de coordenadas no es lineal (por ejemplo, coord_polar()) y, de ser así, emite una advertencia porque nuestro resorte no está diseñado para funcionar en ese contexto.

  • Utiliza el sistema de coordenadas para reescalar la estética posicional llamando al método transform() para el objeto coord. Esto reasigna toda la estética posicional para que se encuentre entre 0 y 1, siendo 0 el valor más bajo visible en nuestra ventana gráfica (expansiones de escala incluidas) y 1 el más alto. Con esta reasignación las coordenadas están listas para pasar al grob.

  • Pasamos un conjunto de parámetros gráficos al grob usando la función grid gpar(). No todos los grobs se preocupan por todas las entradas en gpar() y dado que estamos construyendo una línea, solo nos preocupamos por los parámetros gráficos que polylineGrob() entiende, a saber: col (color de trazo), lwd (línea ancho), lty (tipo de línea), lineend (la forma del terminador de la línea).

Ahora que GeomSpring está definido, todo lo que queda es crear una función constructora que el usuario pueda llamar:

geom_spring <- function(mapping = NULL, 
                        data = NULL, 
                        stat = "identity", 
                        position = "identity", 
                        ..., 
                        n = 50, 
                        lineend = "butt", 
                        na.rm = FALSE, 
                        show.legend = NA, 
                        inherit.aes = TRUE) {
  layer(
    data = data, 
    mapping = mapping, 
    stat = stat, 
    geom = GeomSpring, 
    position = position, 
    show.legend = show.legend, 
    inherit.aes = inherit.aes, 
    params = list(
      n = n, 
      lineend = lineend, 
      na.rm = na.rm, 
      ...
    )
  )
}

Por fin podemos darle un buen uso a nuestra nueva función geom_spring():

ggplot(df) + 
  geom_spring(aes(
    x = x * 100, 
    y = y, 
    xend = xend, 
    yend = yend, 
    diameter = diameter, 
    tension = tension
  ))

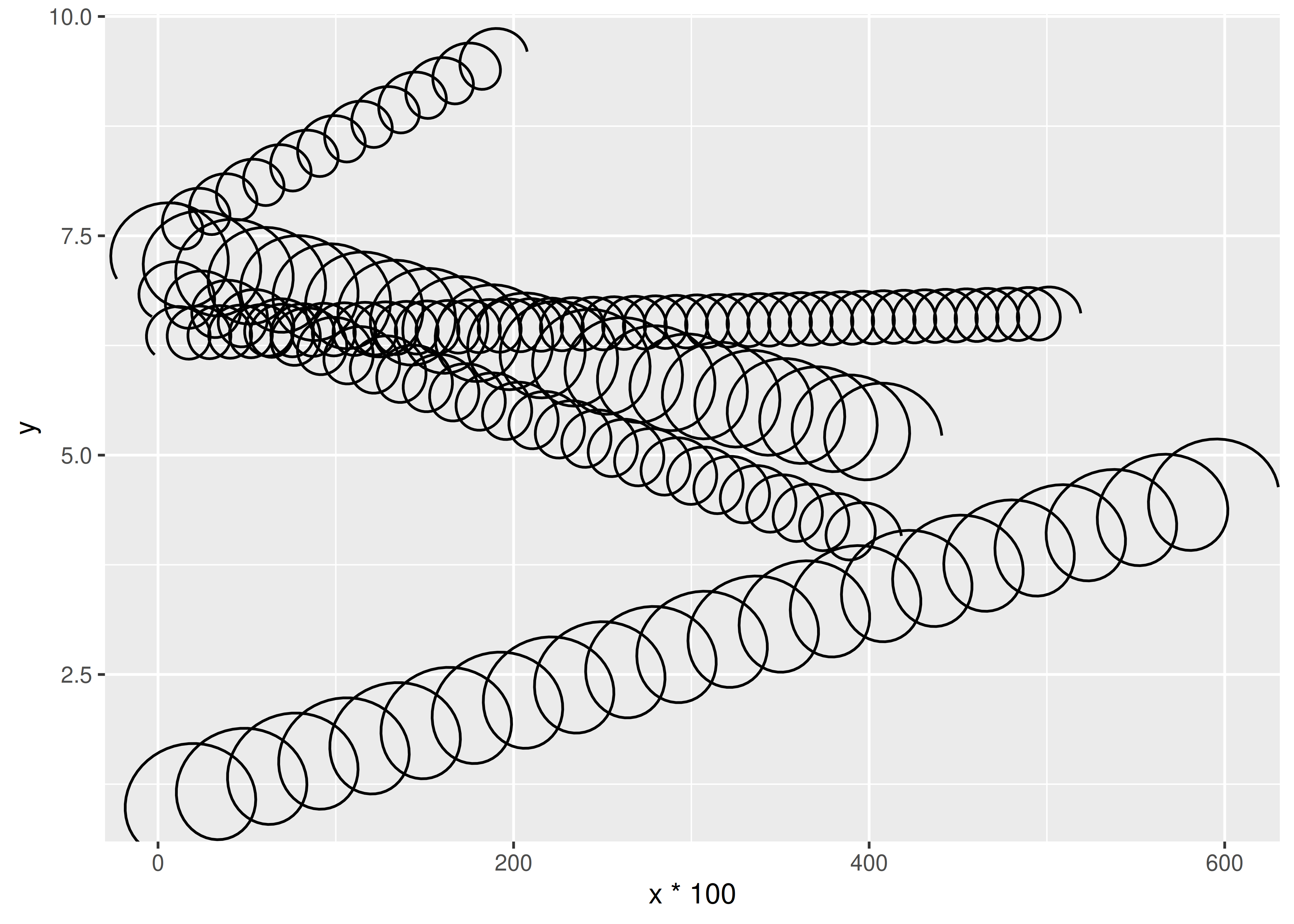
Como puede ver en el resultado anterior, ahora tenemos resortes que se comportan de manera sensata cuando cambia la relación de aspecto de la gráfica o cuando los ejes xey están en diferentes escalas. Cambiar el tamaño del gráfico activará un nuevo cálculo de la ruta correcta, por lo que seguirá luciendo como debería.

21.6.3 Post mortem

Por fin hemos llegado a la geom de primavera que nos propusimos realizar. La estética del diámetro de nuestro resorte tiene un comportamiento similar a la estética del ancho de línea, en el sentido de que permanece fija al cambiar el tamaño y/o cambiar la relación de aspecto del gráfico. Todavía hay mejoras que podríamos (y quizás deberíamos) hacer. Lo más notable es que nuestra función create_spring() permanece sin vectorizar y debe llamarse para cada resorte por separado. Vectorizar correctamente esta función permitirá una aceleración considerable al renderizar muchos resortes (si alguna vez fuera necesario). Dejaremos esto como ejercicio para el lector.

Aunque la geom ya está terminada, todavía nos queda un poco de trabajo por hacer. Necesitamos crear una escala de diámetro y proporcionar claves de leyenda que puedan comunicar correctamente el diámetro y la tensión. Este será el tema de la sección final.

21.7 Parte 5: Escalas

El último paso de nuestro proceso es definir nuevas escalas. Queremos hacer esto porque hemos definido dos nuevas estéticas (diámetro y tensión) y nos gustaría que los usuarios pudieran escalarlas. No hay nada de malo en definir una nueva estética sin proporcionar una escala, lo que significa que los valores mapeados se pasan sin cambios, pero si queremos que los usuarios tengan cierto control y la posibilidad de una leyenda, necesitaremos proporcionar escalas. por la estetica. Este es el objetivo de esta sección final.

21.7.1 Escalada

Afortunadamente, en comparación con el trabajo que hemos realizado hasta ahora, crear nuevas escalas no es una tarea enorme. Discutimos las ideas básicas en Sección 20.5 y podemos aplicar esos conceptos aquí sin demasiado dolor. Nuestra tarea principal es crear una función con el nombre apropiado que genere un objeto Scale. La mayoría de las funciones de escala son simples envoltorios alrededor de una de las tres funciones constructoras de escala fundamentales, continuous_scale(), discrete_scale() y binned_scale(). Así es como lo hacemos para la estética de la tensión:

scale_tension_continuous <- function(..., range = c(0.1, 1)) {
  continuous_scale(
    aesthetics = "tension", 
    scale_name = "tension_c", 
    palette = scales::rescale_pal(range), 
    ...
  )
}

Esta función scale_tension_continuous() indica a qué aesthetics se aplica, proporciona un scale_name explícito y proporciona una función palette que transforma el dominio de entrada al rango de salida. Todos los demás argumentos que normalmente esperaría ver en una función de escala, como name, breaks, limits, se pasan a continuous_scale() con los puntos ....
Para la estética de la tensión, esperamos que los usuarios la apliquen sólo a escalas continuas, por lo que es conveniente definir scale_tension() como un alias para scale_tension_continuous():

scale_tension <- scale_tension_continuous

Finalmente, como no queremos que la gente intente mapear la estética de la tensión en datos discretos, también definiremos una función scale_tension_discrete() que siempre arroja un error:

scale_tension_discrete <- function(...) {
  rlang::abort("Tension cannot be used with discrete data")
}

La razón por la que esto funciona es que ggplot2 asigna la escala predeterminada para la estética buscando una función llamada scale_<aesthetic-name>_<data-type>, por lo que cada vez que el usuario asigna la tensión estética a una variable discreta, ggplot2 encontrará la función scale_tension_discrete() y arroja el error. Esta es también la razón por la que es importante incluir scale_tension_continuous() incluso cuando esperamos que la mayoría de los usuarios utilicen el alias scale_tension().

Las funciones de escala para la estética del diámetro son sólo un poco más complicadas:

scale_diameter_continuous <- function(..., 
                                      range = c(0.25, 0.7), 
                                      unit = "cm") {
  range <- grid::convertWidth(
    unit(range, unit), 
    "cm", 
    valueOnly = TRUE
  )
  continuous_scale(
    aesthetics = "diameter", 
    scale_name = "diameter_c", 
    palette = scales::rescale_pal(range), 
    ...
  )
}
scale_diameter <- scale_diameter_continuous
scale_tension_discrete <- function(...) {
  rlang::abort("Diameter cannot be used with discrete data")
}

El único cambio que hicimos con respecto a las escalas de tension es que permitimos al usuario definir en qué unidad se debe medir el rango de diámetro. Dado que el geom espera centímetros, convertiremos el rango a eso antes de pasarlo al constructor de escalas. De esa manera, el usuario es libre de utilizar cualquier unidad absoluta que le parezca natural.

Con nuestras escalas definidas, echemos un vistazo:

ggplot(df) + 
  geom_spring(aes(
    x = x, 
    y = y, 
    xend = xend, 
    yend = yend, 
    tension = tension, 
    diameter = diameter
  )) + 
  scale_tension(range = c(0.1, 5)) 
#> Warning: The `scale_name` argument of `continuous_scale()` is deprecated as of ggplot2
#> 3.5.0.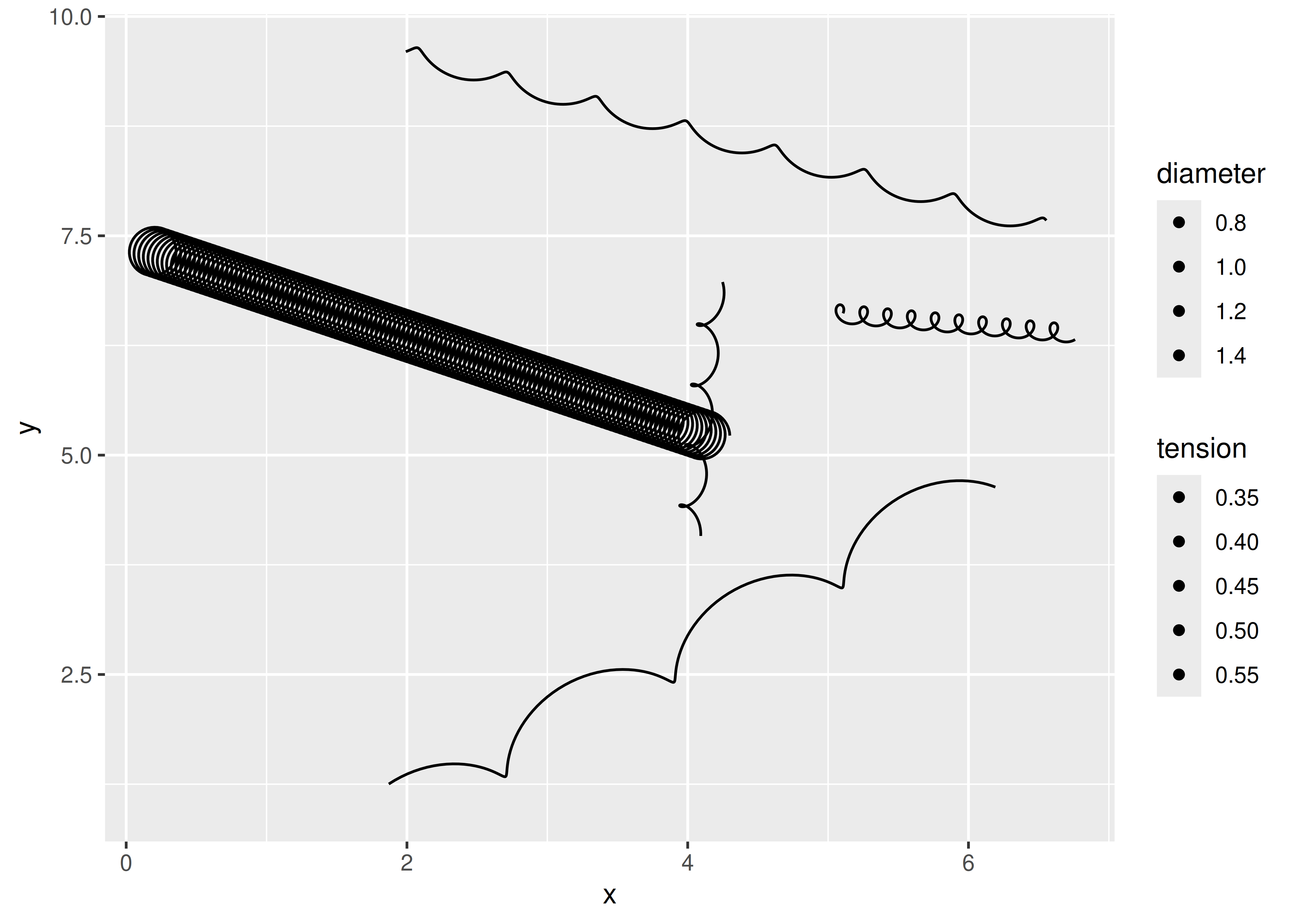

En este resultado podemos ver que las escalas predeterminadas funcionan (es decir, no agregamos una escala explícita para el diámetro pero el gráfico se representa correctamente), al igual que las escalas personalizadas (es decir, llamamos explícitamente scale_tension()).

El resultado también nos dice que nuestro trabajo no ha terminado porque la leyenda no es muy útil. La razón de esto es que nuestra geom está utilizando el constructor de claves de leyenda predeterminado, draw_key_point(). Esta función no entiende nuestra nueva estética, por lo que la ignora por completo. Podemos solucionar este problema definiendo una función clave de leyenda personalizada, draw_key_spring().

21.7.2 draw_key_spring

Echemos un vistazo a cómo se escribe un constructor de claves, inspeccionando el código fuente para draw_key_point(). Afortunadamente, estas son funciones bastante simples que toman un marco de datos de valores estéticos y devuelven un grob apropiado que proporciona las representaciones que se muestran en la clave de leyenda:

draw_key_point
#> function(data, params, size) {
#>   if (is.null(data$shape)) {
#>     data$shape <- 19
#>   } else if (is.character(data$shape)) {
#>     data$shape <- translate_shape_string(data$shape)
#>   }
#> 
#>   # NULL means the default stroke size, and NA means no stroke.
#>   stroke_size <- data$stroke %||% 0.5
#>   stroke_size[is.na(stroke_size)] <- 0
#> 
#>   pointsGrob(0.5, 0.5,
#>     pch = data$shape,
#>     gp = gpar(
#>       col = alpha(data$colour %||% "black", data$alpha),
#>       fill = fill_alpha(data$fill %||% "black", data$alpha),
#>       fontsize = (data$size %||% 1.5) * .pt + stroke_size * .stroke / 2,
#>       lwd = stroke_size * .stroke / 2
#>     )
#>   )
#> }
#> <bytecode: 0x55b33a8e4c10>
#> <environment: namespace:ggplot2>

En este código, data es un marco de datos con una sola fila que proporciona los valores estéticos que se utilizarán para la clave, params son los parámetros geográficos de la capa y size es el tamaño del área clave en centímetros. El operador %||%, que se ve a menudo en el código fuente de tidyverse, se usa para proporcionar valores predeterminados siempre que una variable tiene un valor nulo:

`%||%` <- function(x, y) {
  if (is.null(x)) y else x
}

Para definir nuestra función draw_key_spring(), necesitamos crear una función análoga que use springGrob() para dibujar la clave:

draw_key_spring <- function(data, params, size) {
  springGrob(
    x0 = 0, 
    y0 = 0, 
    x1 = 1, 
    y1 = 1,
    diameter = unit(data$diameter, "cm"), 
    tension = data$tension,
    gp = gpar(
      col = alpha(data$colour %||% "black", data$alpha),
      lwd = (data$size %||% 0.5) * .pt,
      lty = data$linetype %||% 1
    ),
    vp = viewport(clip = "on")
  )
}

La única parte de este código que puede resultar desconocida es la pequeña floritura (no estrictamente necesaria) que define una ventana gráfica de recorte para nuestro grob usando el argumento vp. La razón por la que agregamos esto es para garantizar que los resortes dibujados en las claves de leyenda estén estrictamente contenidos dentro de sus cajas y no se extiendan a las áreas clave vecinas.

Ahora que tenemos esta función, todo lo que tenemos que hacer es decirle a GeomSpring que la use al dibujar la clave de leyenda. Eso es bastante sencillo: todo lo que tenemos que hacer es cambiar el método draw_key() de nuestro Geom existente:

GeomSpring$draw_key <- draw_key_spring

Con ese cambio final nuestra leyenda empieza a tener sentido:

ggplot(df) + 
  geom_spring(aes(
    x = x, 
    y = y, 
    xend = xend, 
    yend = yend, 
    tension = tension, 
    diameter = diameter
  )) + 
  scale_tension(range = c(0.1, 5))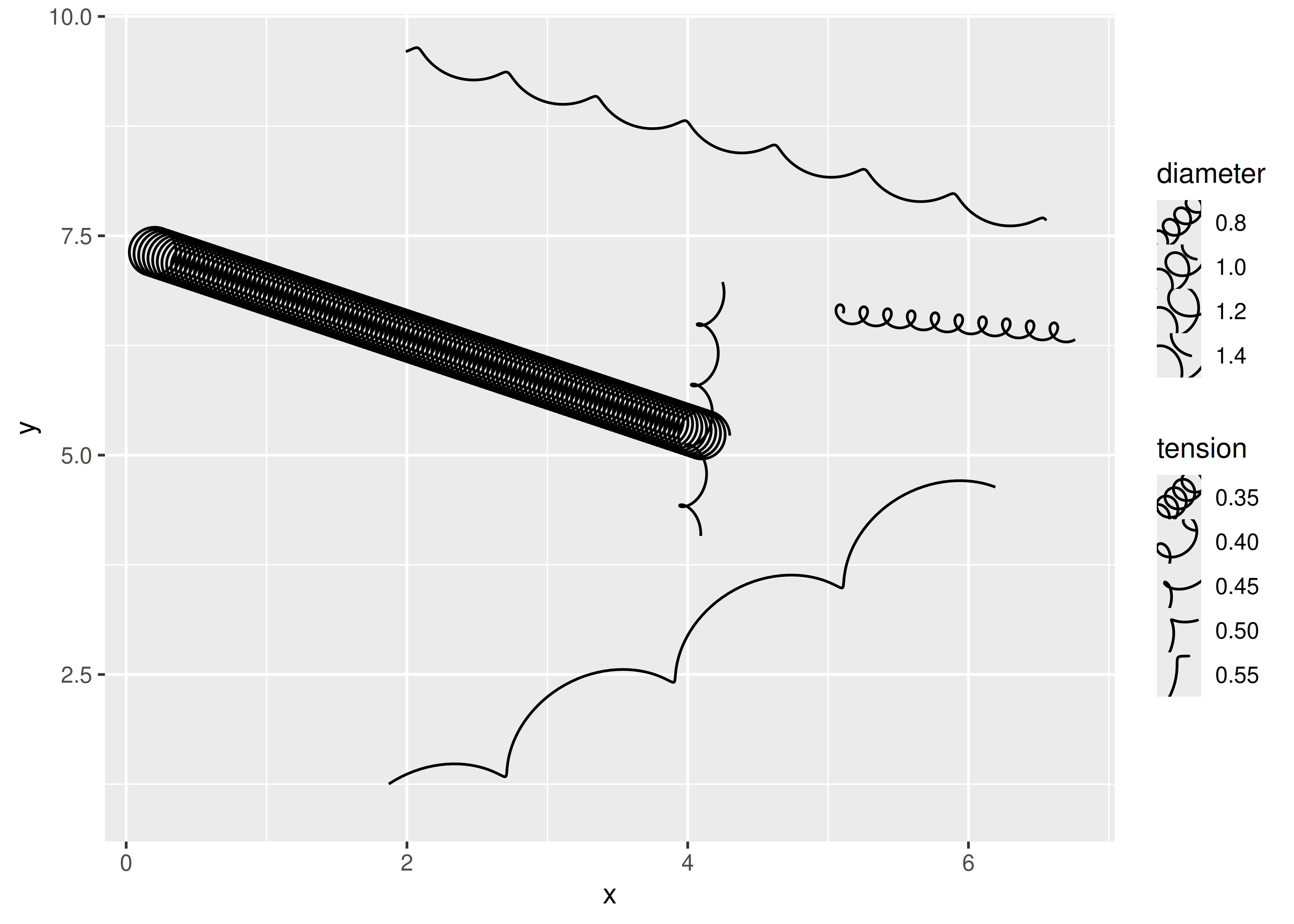

El tamaño de clave predeterminado es un poco estrecho para nuestra clave, pero eso es algo que el usuario deberá hacer: ggplot2 no conoce la estética del diameter y no puede escalar el tamaño de la clave tan inteligentemente como lo hace con la estético size.

ggplot(df) + 
  geom_spring(aes(
    x = x, 
    y = y, 
    xend = xend, 
    yend = yend, 
    tension = tension, 
    diameter = diameter
  )) + 
  scale_tension(range = c(0.1, 5)) +
  theme(legend.key.size = unit(1, "cm"))

Convenientemente, nuestra nueva clave de leyenda se utilizará para todas las estéticas escaladas, no solo para diameter y tension, asegurando así que el estilo de la clave siempre coincidirá con el estilo de la capa:

ggplot(df) + 
  geom_spring(aes(
    x = x, 
    y = y, 
    xend = xend, 
    yend = yend, 
    colour = class
  )) + 
  theme(legend.key.size = unit(1, "cm"))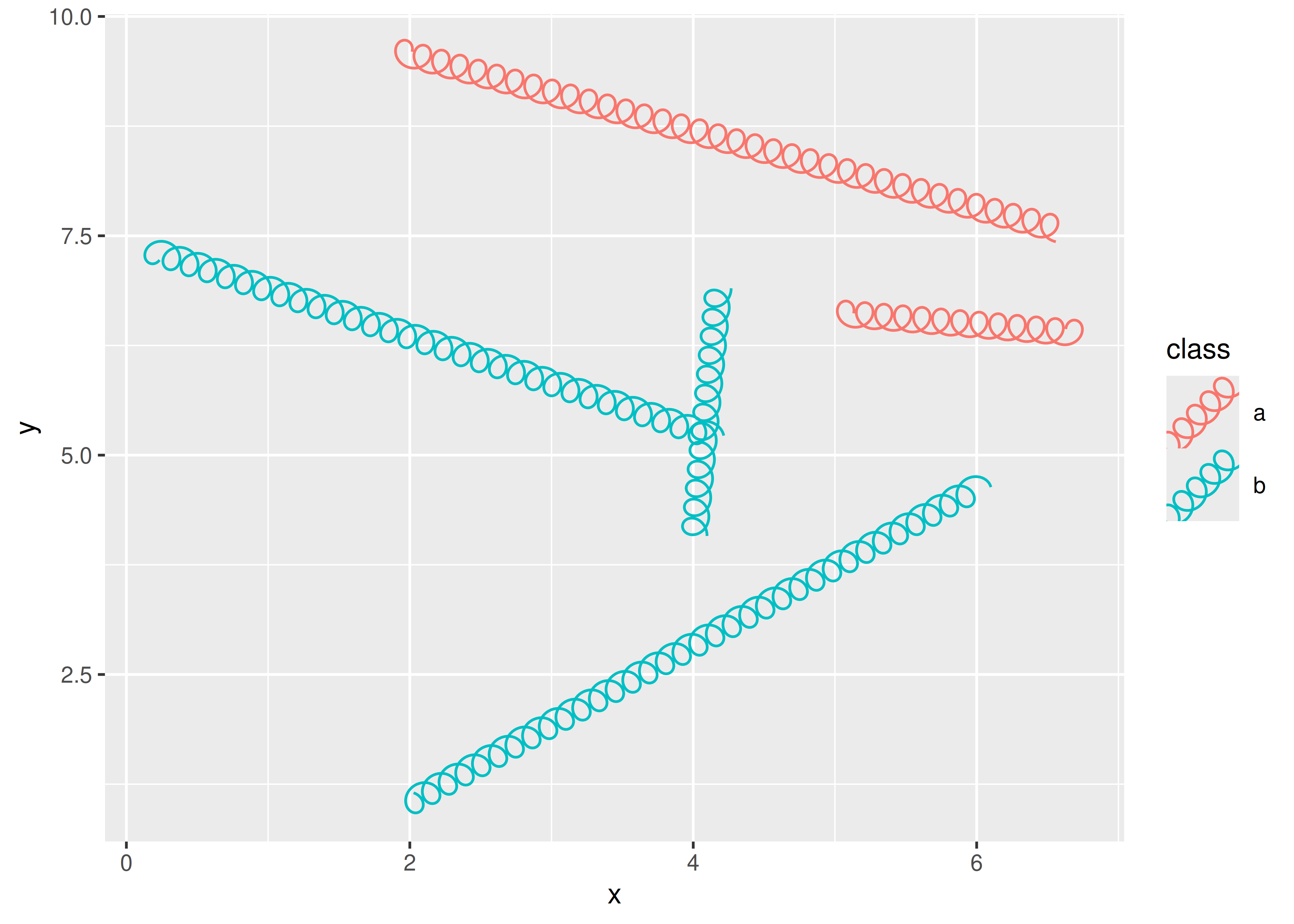

21.7.3 Post mortem

Con esto concluye nuestro estudio de caso detallado sobre la creación de una geom de resorte. Con suerte, ha quedado claro que hay muchas formas diferentes de lograr la misma extensión de geom y que el resultado final depende en gran medida de tus necesidades y de la cantidad de energía que quieras ponerle. El estudio de caso se centró en capas y (en menor medida) escalas, pero con suerte puedes usar los ejemplos más simples de Capítulo 20 como guía si deseas explorar otros tipos de extensiones de ggplot2. También puedes estudiar el código fuente de las clases faceta y coord en ggplot2 y las extensiones disponibles en ggforce y otros paquetes.

Murrell, Paul. 2018. R Graphics. Third. Chapman & Hall/CRC. https://www.stat.auckland.ac.nz/~paul/RG3e/.

  1. Si tiene experiencia en estadística, reconocerá que esto es más o menos análogo a cómo se calcula una estadística z.↩︎

  2. Si tiene experiencia en el desarrollo de paquetes, es posible que se pregunte acerca de la opción de usar rlang::abort() en lugar de usar la función base stop(). Ciertamente podríamos haber elegido usar la función base R aquí, pero como ggplot2 usa el paquete rlang, en este caso hay muy poca diferencia.↩︎

  3. Si planeáramos agrupar este código como un paquete R, podríamos ampliarlo y escribir pruebas unitarias formales para create_spring() usando el paquete testthat.↩︎

  4. Por convención, las clases de ggproto siempre usan CamelCase para nombrar y la nueva clase siempre se guarda en una variable con el mismo nombre.↩︎

  5. Como mencionamos anteriormente, ggproto no hace una fuerte distinción entre métodos y campos. Los objetos Stat esperan que compute_group() sea una función, por lo que nos referimos a compute_group() como método porque esa es la terminología estándar en la programación orientada a objetos. Por el contrario, Stat espera que required_aes sea una variable, por eso lo llamamos campo.↩︎