library(tidygraph)
graph <- play_erdos_renyi(n = 10, p = 0.2) %>%
activate(nodes) %>%
mutate(class = sample(letters[1:4], n(), replace = TRUE)) %>%
activate(edges) %>%
arrange(.N()$class[from])
#> Warning: `play_erdos_renyi()` was deprecated in tidygraph 1.3.0.
#> ℹ Please use `play_gnp()` instead.
graph
#> # A tbl_graph: 10 nodes and 18 edges
#> #
#> # A directed simple graph with 1 component
#> #
#> # Edge Data: 18 × 2 (active)
#> from to
#> <int> <int>
#> 1 9 2
#> 2 5 10
#> 3 8 5
#> 4 8 10
#> 5 9 8
#> 6 9 10
#> # ℹ 12 more rows
#> #
#> # Node Data: 10 × 1
#> class
#> <chr>
#> 1 a
#> 2 d
#> 3 c
#> # ℹ 7 more rows7 Redes
You are reading the work-in-progress third edition of the ggplot2 book. This chapter is currently a dumping ground for ideas, and we don’t recommend reading it.
Al igual que los mapas y los datos espaciales, las redes y los gráficos ocupan una parte especial del panorama de la visualización, pero mientras que los datos espaciales difieren en su mayoría de los trazados regulares en el uso de proyecciones, las redes aportan su propia estructura de datos, así como sus propios paradigmas de visualización. Debido a estas complicaciones, las redes no son compatibles directamente con ggplot2. Varios esfuerzos a lo largo de los años han intentado agregar esta pieza faltante y en este capítulo veremos cómo usar ggraph para visualización de redes. Otros paquetes que ofrecen algunas de las mismas funciones incluyen geomnet, ggnetwork, y GGally para gráficas de redes regulares, y ggtree y ggdendro para visualización de árboles específicamente.
7.1 ¿Qué son los datos de red?
Las redes (o gráficos como se llama su concepto matemático) son datos que constan de entidades (nodos o vértices) y su relación (bordes o enlaces). Tanto los nodos como los bordes pueden tener datos adicionales adjuntos y, además, los bordes pueden considerarse dirigidos o no dirigidos dependiendo de la naturaleza de la conexión (una red que codifica amistad mutua tendría bordes no dirigidos, mientras que una red ancestral tendrá bordes dirigidos porque hijo de no es una relación simétrica).
La naturaleza de los datos de la red significa que no se pueden representar fácilmente en un único marco de datos, lo cual es una de las complicaciones clave de su uso con ggplot2. Sin embargo, se puede codificar como dos marcos de datos interrelacionados, uno que codifica los nodos y el otro que codifica los bordes. Este es el enfoque utilizado en tidygraph, que es el paquete de manipulación de datos subyacente a ggraph. Por lo tanto, para hacer un mejor uso de ggraph es beneficioso comprender un poco sobre tidygraph.
7.1.1 Una API de manipulación de red ordenada
tidygraph puede considerarse, ante todo, una API de dplyr para datos de red, que permite la misma semántica para manipular redes que se conoce en dplyr. Se puede ver un ejemplo de esto a continuación, donde creamos un gráfico aleatorio utilizando el método de muestreo Erdős-Rényi, asignamos una etiqueta aleatoria a los nodos y clasificamos los bordes según la etiqueta de su nodo de origen.
Si bien mutate(), arrange() y n() son bien conocidos, podemos ver algunas funciones nuevas que necesitan explicación: activate() informa a tidygraph en qué parte de la red deseas trabajar en, ya sea nodes o edges. Además, vemos el uso de .N() que da acceso a los datos del nodo del gráfico actual incluso cuando se trabaja con los bordes (también hay una función correspondiente .E() para acceder a los datos de los bordes, y . .G() para acceder a todo el gráfico).
7.1.2 Conversión
Los datos de la red a menudo se presentan en una variedad de formatos diferentes dependiendo de dónde se obtengan. tidygraph comprende la mayoría de las diferentes clases utilizadas en R para datos de red y estas se pueden convertir usando as_tbl_graph(). A continuación se muestra un ejemplo de conversión de un marco de datos codificado como lista de bordes, así como de conversión del resultado de hclust().
hs_graph <- as_tbl_graph(highschool, directed = FALSE)
hs_graph
#> # A tbl_graph: 70 nodes and 506 edges
#> #
#> # An undirected multigraph with 1 component
#> #
#> # Node Data: 70 × 0 (active)
#> #
#> # Edge Data: 506 × 3
#> from to year
#> <int> <int> <dbl>
#> 1 1 13 1957
#> 2 1 14 1957
#> 3 1 20 1957
#> # ℹ 503 more rowsluv_clust <- hclust(dist(luv_colours[, 1:3]))
luv_graph <- as_tbl_graph(luv_clust)
luv_graph
#> # A tbl_graph: 1313 nodes and 1312 edges
#> #
#> # A rooted tree
#> #
#> # Node Data: 1,313 × 4 (active)
#> height leaf label members
#> <dbl> <lgl> <chr> <int>
#> 1 0 TRUE "101" 1
#> 2 0 TRUE "427" 1
#> 3 778. FALSE "" 2
#> 4 0 TRUE "571" 1
#> 5 0 TRUE "426" 1
#> 6 0 TRUE "424" 1
#> # ℹ 1,307 more rows
#> #
#> # Edge Data: 1,312 × 2
#> from to
#> <int> <int>
#> 1 3 1
#> 2 3 2
#> 3 8 6
#> # ℹ 1,309 more rowsPodemos ver que tidygraph agrega automáticamente información adicional al realizar la conversión, p. la columna year en los datos de la escuela secundaria y las propiedades label y leaft de los nodos en la agrupación jerárquica.
7.1.3 Algoritmos
Si bien simplemente manipular las redes es agradable, el beneficio real de las redes proviene de las diferentes operaciones que se pueden realizar en ellas utilizando la estructura subyacente. tidygraph tiene un amplio soporte para una variedad de diferentes grupos de algoritmos, como cálculo de centralidad (qué nodo es más central), clasificación (ordenar los nodos para que estén ubicados cerca de aquellos a los que están conectados), agrupación (encontrar clústeres dentro de la red), etc. La API del algoritmo está diseñada para usarse dentro de mutate() y siempre devolverá un vector con una longitud y un orden que coincidan con los nodos o bordes. Además, no requiere que especifiques el gráfico o los nodos que deseas calcular, ya que esto se proporciona implícitamente en la llamada mutate(). Como ejemplo, calcularemos la centralidad de los nodos en nuestro gráfico de muestra usando el algoritmo PageRank y ordenaremos los nodos de acuerdo con eso:
graph %>%
activate(nodes) %>%
mutate(centrality = centrality_pagerank()) %>%
arrange(desc(centrality))
#> # A tbl_graph: 10 nodes and 18 edges
#> #
#> # A directed simple graph with 1 component
#> #
#> # Node Data: 10 × 2 (active)
#> class centrality
#> <chr> <dbl>
#> 1 c 0.220
#> 2 a 0.165
#> 3 c 0.140
#> 4 a 0.128
#> 5 c 0.128
#> 6 a 0.0703
#> # ℹ 4 more rows
#> #
#> # Edge Data: 18 × 2
#> from to
#> <int> <int>
#> 1 6 7
#> 2 2 1
#> 3 8 2
#> # ℹ 15 more rows7.1.4 ¿Quieren más?
Esto es sólo un breve vistazo a tidygraph, con el fin de comprender ggraph. Si está interesado en obtener más información, el sitio web de tidygraph ofrece una descripción general de todas las funcionalidades del paquete: https://tidygraph.data-imaginist.com
7.2 Visualizando redes
ggraph se basa en tidygraph y ggplot2 para permitir una gramática de gráficos completa y familiar para datos de red. Aún así, es un poco diferente de la mayoría de los paquetes de extensión ggplot2 ya que funciona con otro tipo de datos que es fundamentalmente diferente de los datos tabulares. Más aún, la mayoría de las visualizaciones de redes no se preocupan por asignar variables a la estética x e y, ya que se preocupan por mostrar la topología de la red más que las relaciones entre dos variables. Para mostrar la topología de la red, se emplea el concepto de diseños. Los diseños son algoritmos que utilizan la estructura de la red para calcular (a menudo arbitrarios) los valores x e y para cada nodo que luego pueden usarse con fines de visualización. Para decirlo de otra manera, al trazar datos tabulares, la estética x e y casi siempre se asignan a variables existentes en los datos (o transformaciones estadísticas de datos existentes), mientras que al trazar datos de red x e y. se asignan a valores derivados de la topología de la red y que por sí solos no tienen sentido.
7.2.1 Configurar la visualización
Mientras que un gráfico ggplot2 normal se inicializa con una llamada ggplot(), un gráfico ggraph se inicializa con una llamada ggraph(). El primer argumento son los datos, que pueden ser un tbl_graph o cualquier objeto convertible en uno. El segundo argumento es una función de diseño y cualquier argumento adicional se pasará a esa función. El diseño predeterminado elegirá un diseño apropiado según el tipo de gráfico que proporcione, pero si bien suele ser un punto de partida decente, siempre debe tomar el control y explorar los diferentes diseños disponibles. Las redes son conocidas por su capacidad para mostrar imágenes no gráficas. Relaciones existentes o exageradas en algunos diseños. Hay más diseños que los descritos en esta sección. La Guía de introducción a los diseños le brindará aún más información y le mostrará todos los diferentes diseños proporcionados por ggraph.
7.2.1.1 Especificación de un diseño
El argumento de diseño puede tomar una cadena o una función. Si se proporciona una cadena, el nombre coincidirá con uno de los diseños integrados (de los cuales hay muchos). Si se proporciona una función, se supone que la función toma un tbl_graph y devuelve un marco de datos con al menos una columna xey y con el mismo número de filas que nodos en el gráfico de entrada. A continuación podemos ver ejemplos de cómo usar el diseño predeterminado, especificar un diseño específico y proporcionar argumentos para el diseño (que se evalúan en el contexto del gráfico de entrada):
library(ggraph)
ggraph(hs_graph) +
geom_edge_link() +
geom_node_point()
#> Using "stress" as default layout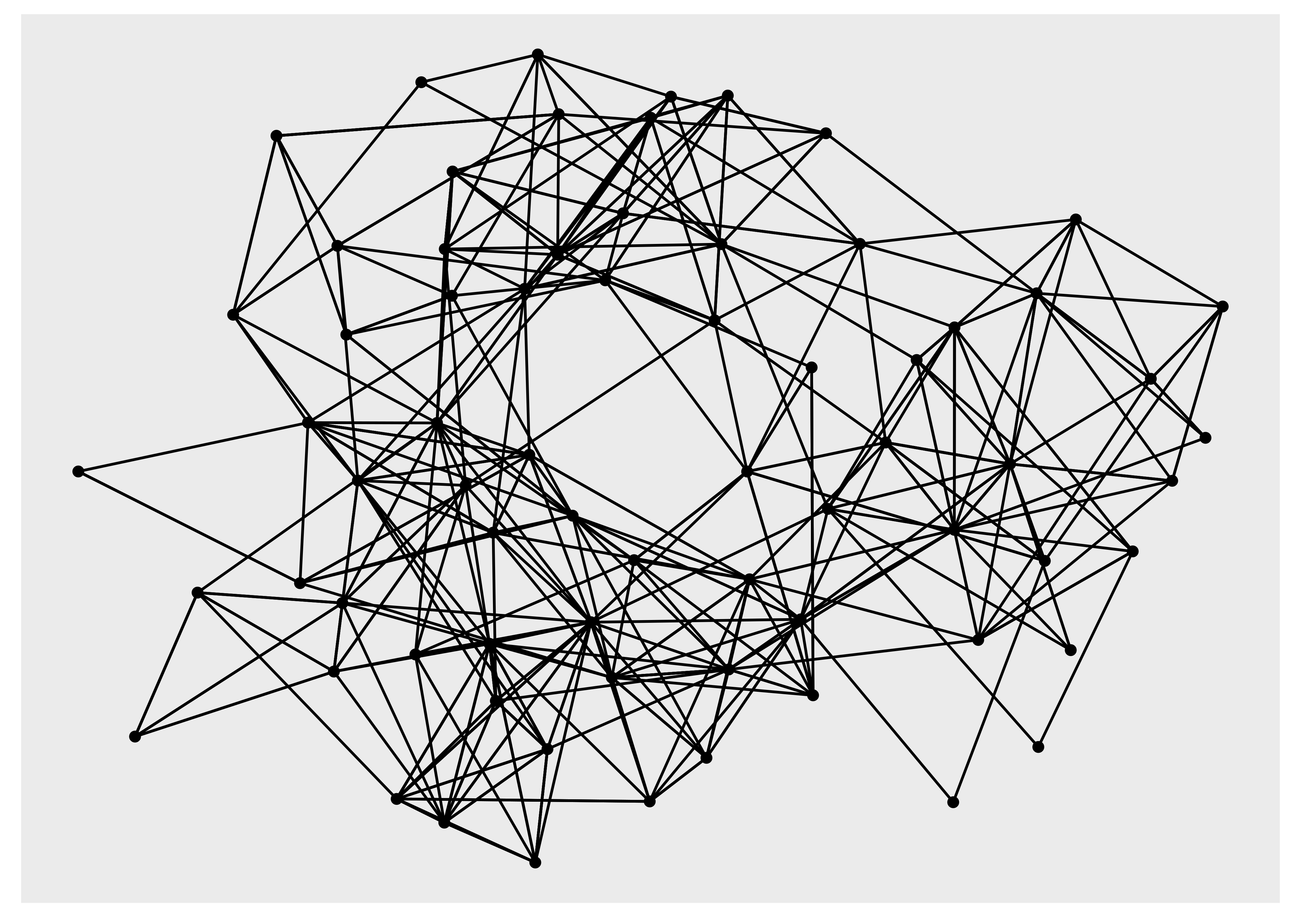
ggraph(hs_graph, layout = "drl") +
geom_edge_link() +
geom_node_point()
hs_graph <- hs_graph %>%
activate(edges) %>%
mutate(edge_weights = runif(n()))
ggraph(hs_graph, layout = "stress", weights = edge_weights) +
geom_edge_link(aes(alpha = edge_weights)) +
geom_node_point() +
scale_edge_alpha_identity()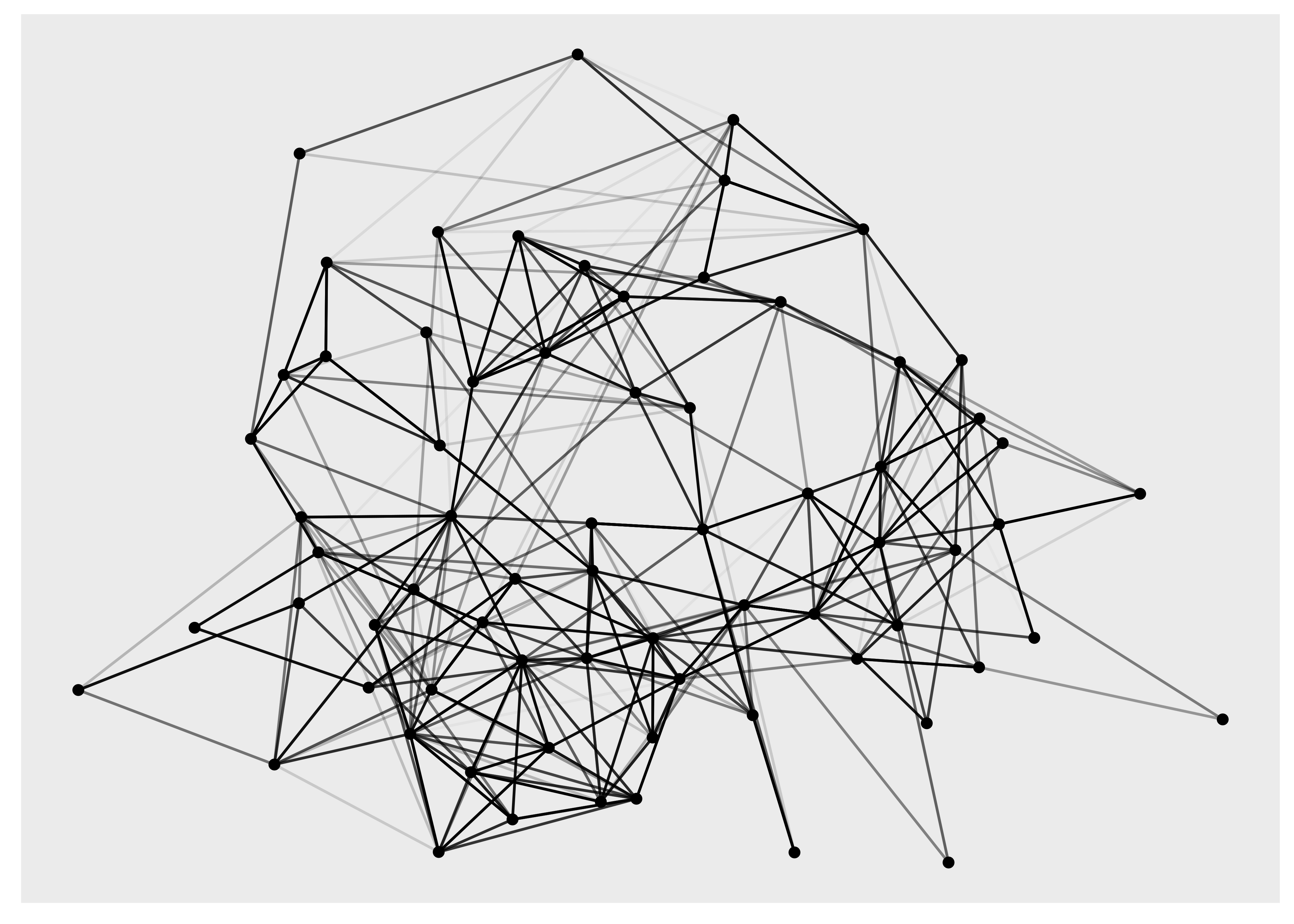
Para mostrar el gráfico de arriba estamos usando las funciones geom_edge_link() y geom_node_point(), y aunque todavía no las hemos discutido, hacen exactamente lo que puedas imaginar: dibujar nodos como puntos y bordes como líneas rectas. .
7.2.1.2 Circularidad
Algunos diseños se pueden utilizar tanto en versión lineal como circular. La forma correcta de cambiar esto en ggplot2 sería usar coord_polar() para cambiar el sistema de coordenadas, pero como solo queremos cambiar la posición de los nodos en el diseño y no afectar los bordes, esto es una función del disposición. Lo siguiente puede mostrar la diferencia:
ggraph(luv_graph, layout = "dendrogram", circular = TRUE) +
geom_edge_link() +
coord_fixed()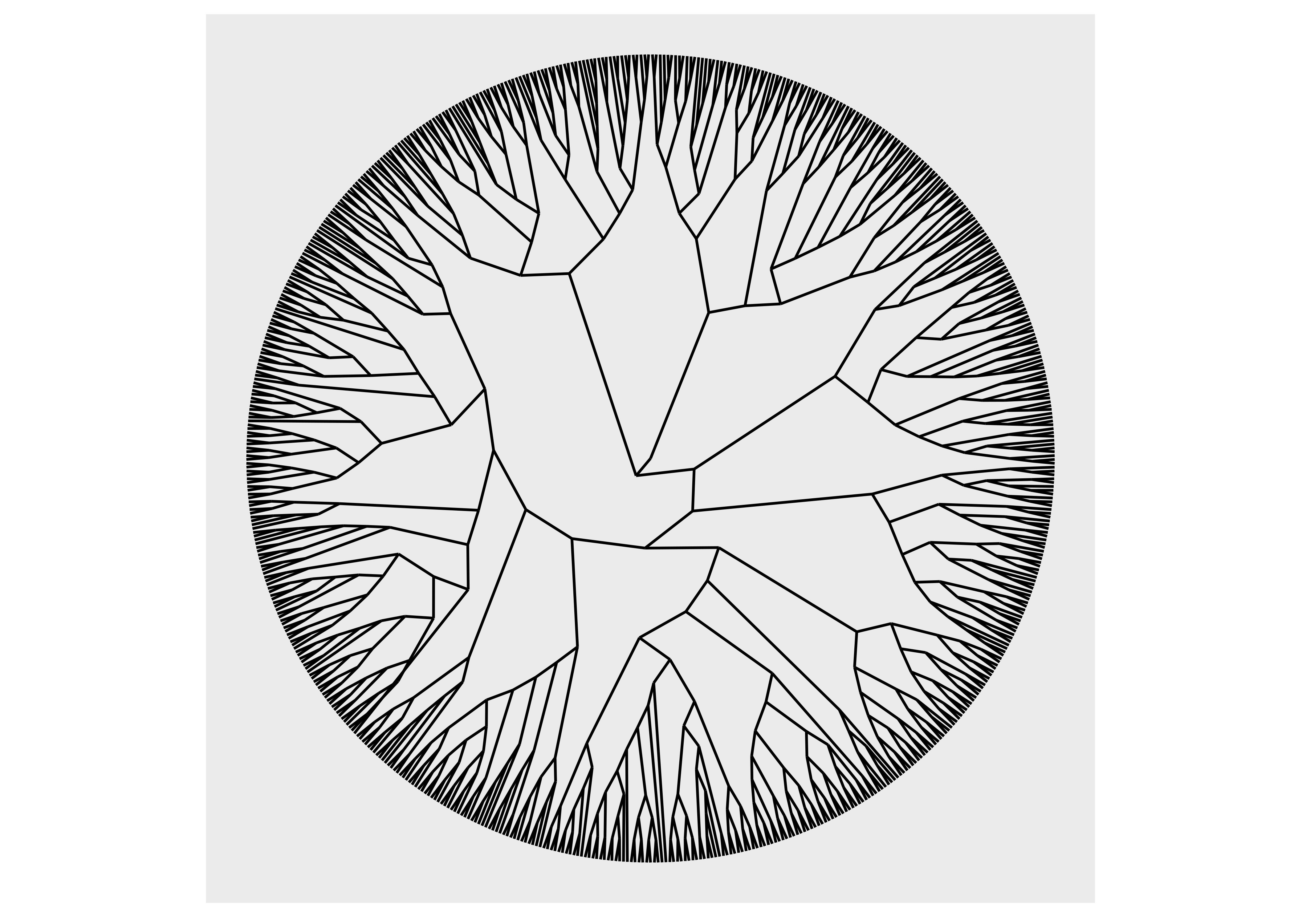
ggraph(luv_graph, layout = "dendrogram") +
geom_edge_link() +
coord_polar() +
scale_y_reverse()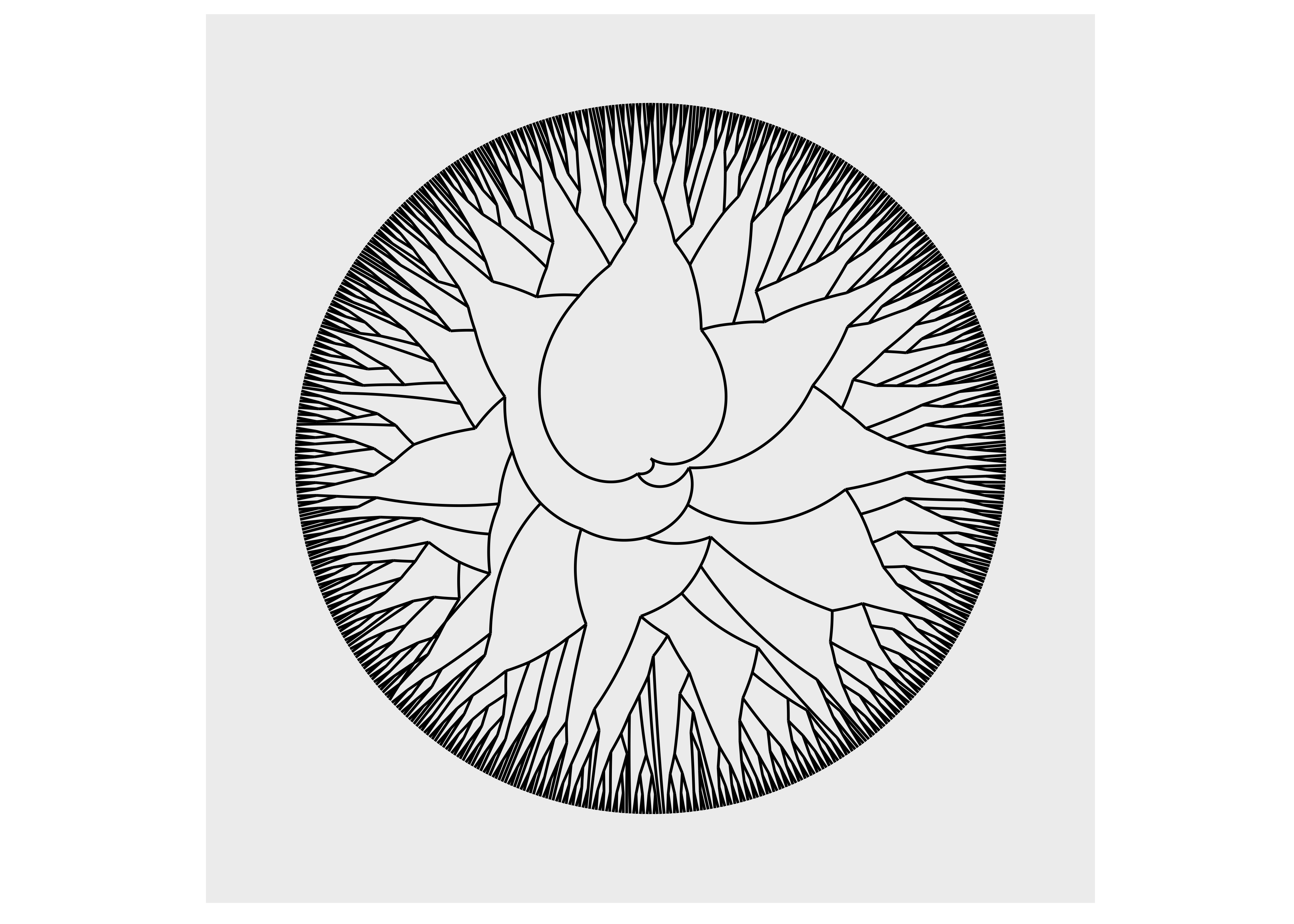
Como podemos ver, usar coord_polar() doblará nuestros bordes, lo cual no es una opción deseable.
7.2.2 Nodos de dibujo
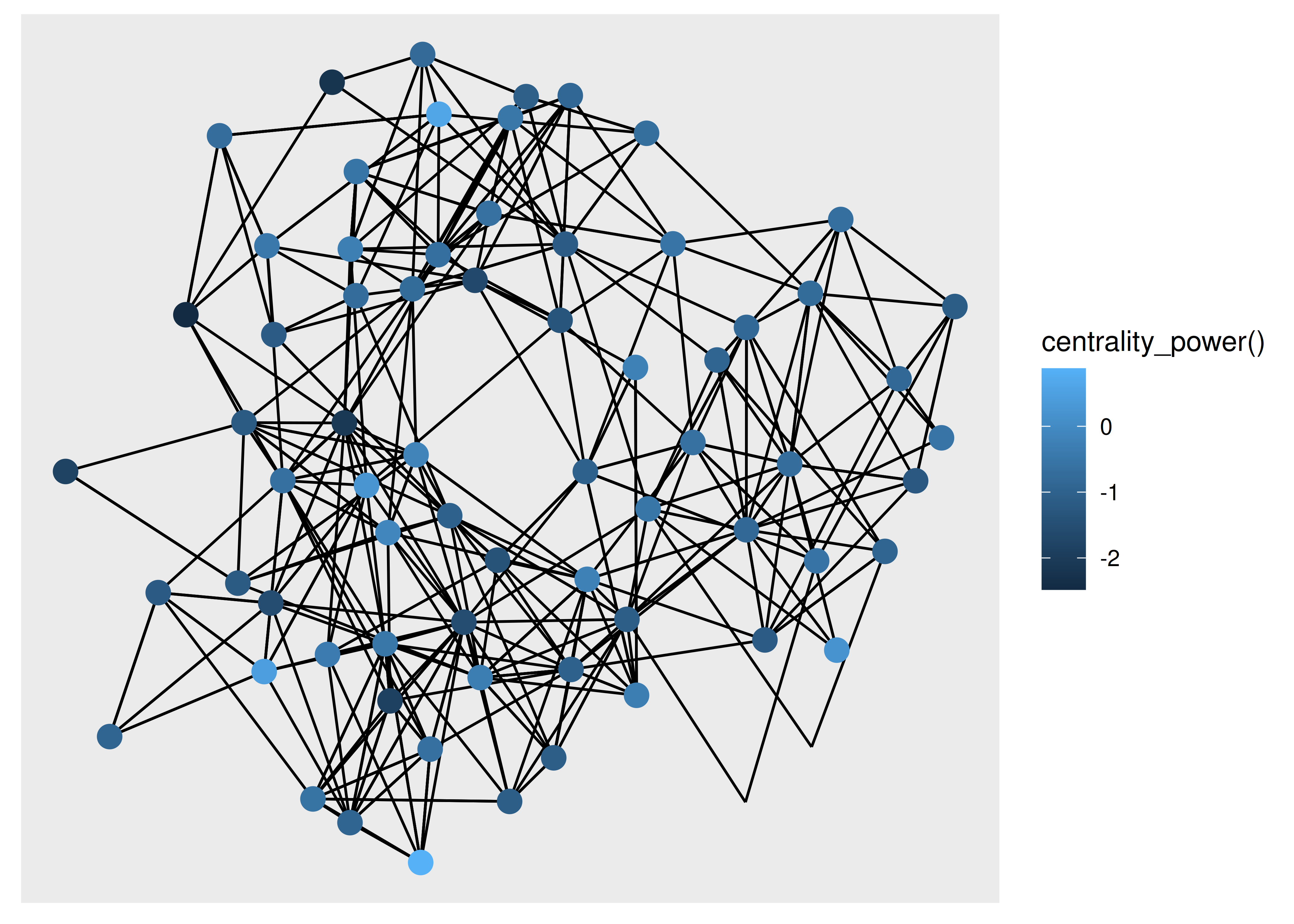
De los dos tipos de datos almacenados en un gráfico, los nodos son, con diferencia, los que más se parecen a lo que estamos acostumbrados a representar. Después de todo, a menudo se muestran como puntos de forma muy parecida a como se muestran las observaciones en un diagrama de dispersión. Si bien conceptualmente es simple, todavía no cubriremos todo lo que hay que saber sobre los nodos, por lo que, al igual que con los diseños, el lector interesado debe consultar la Guía de introducción a los nodos para aprender más. Todas las geoms de dibujo de nodos en ggraph tienen el prefijo geom_node_ y el que es más probable que uses con más frecuencia es geom_node_point(). Si bien superficialmente puede parecerse mucho geom_point() tiene algunas características adicionales que comparte con todas las geomas de nodos y bordes. Primero, no es necesario especificar la estética x e y. Estos vienen dados por el diseño y su mapeo está implícito. En segundo lugar, tienes acceso a una estética de filter que te permite desactivar el dibujo de nodos específicos. En tercer lugar, puede utilizar cualquier algoritmo de tidygraph dentro de aes() y se evaluarán en el gráfico que se visualiza. Para ver esto en acción, trazamos nuestro gráfico de secundaria nuevamente, pero esta vez solo muestra los nodos con más de 2 conexiones y coloreados según su centralidad de poder:
ggraph(hs_graph, layout = "stress") +
geom_edge_link() +
geom_node_point(
aes(filter = centrality_degree() > 2,
colour = centrality_power()),
size = 4
)
Poder usar algoritmos directamente dentro del código de visualización es una forma poderosa de iterar en su visualización, ya que no necesita regresar y cambiar el gráfico de entrada.
Aparte de los puntos, hay geoms más especializados, muchos de ellos vinculados a un tipo específico de diseño. Si uno desea dibujar un mapa de árbol, se necesita geom_node_tile():
ggraph(luv_graph, layout = "treemap") +
geom_node_tile(aes(fill = depth))
#> Warning: Existing variables `height` and `leaf` overwritten by layout variables
7.2.3 Bordes de dibujo
Las geoms de borde tienen muchas más características que las geoms de nodo, principalmente porque hay muchas formas diferentes de conectar dos cosas. No hay forma de abarcarlo todo, tanto en términos de los diferentes tipos de geoms, como de la funcionalidad común que tienen. La Guía de introducción a los bordes ofrecerá una descripción completa.
Ya hemos visto geom_edge_link() en acción, que dibuja una línea recta entre los nodos conectados, pero puede hacer más de lo que ya hemos visto. Debajo del capó, dividirá la línea en un montón de pequeños fragmentos y es posible usarlo para dibujar un degradado a lo largo del borde, por ejemplo. para mostrar dirección:
ggraph(graph, layout = "stress") +
geom_edge_link(aes(alpha = after_stat(index)))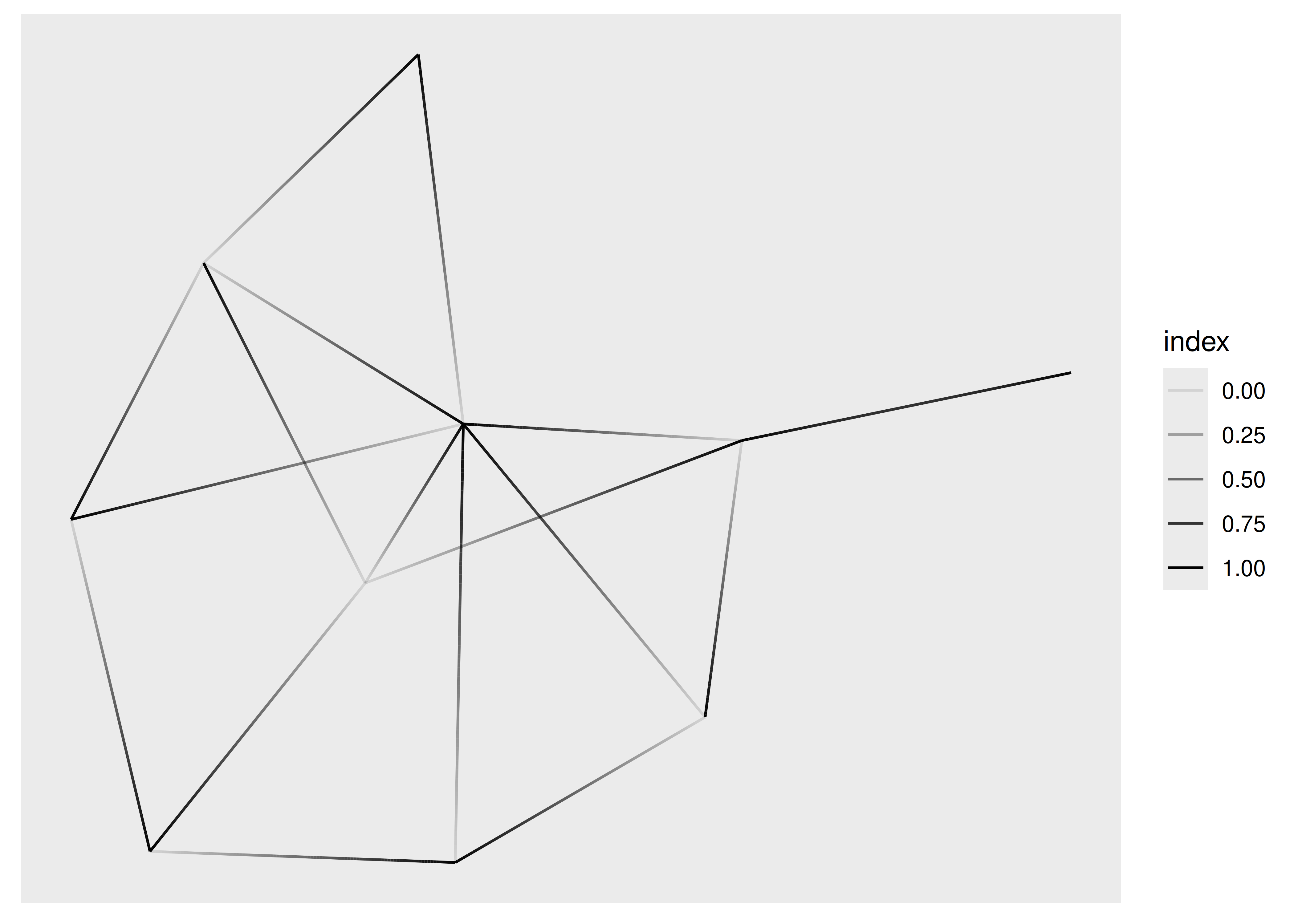
Si está dibujando muchos bordes, esta expansión puede consumir mucho tiempo y ggraph proporciona una versión con el sufijo 0 que lo dibuja como una geom simple (y no le permite dibujar gradientes). Además, para el caso especial en el que desea interpolar entre dos valores en los puntos finales (por ejemplo, variables en los nodos), también existe una versión con el sufijo 2:
ggraph(graph, layout = "stress") +
geom_edge_link2(
aes(colour = node.class),
width = 3,
lineend = "round")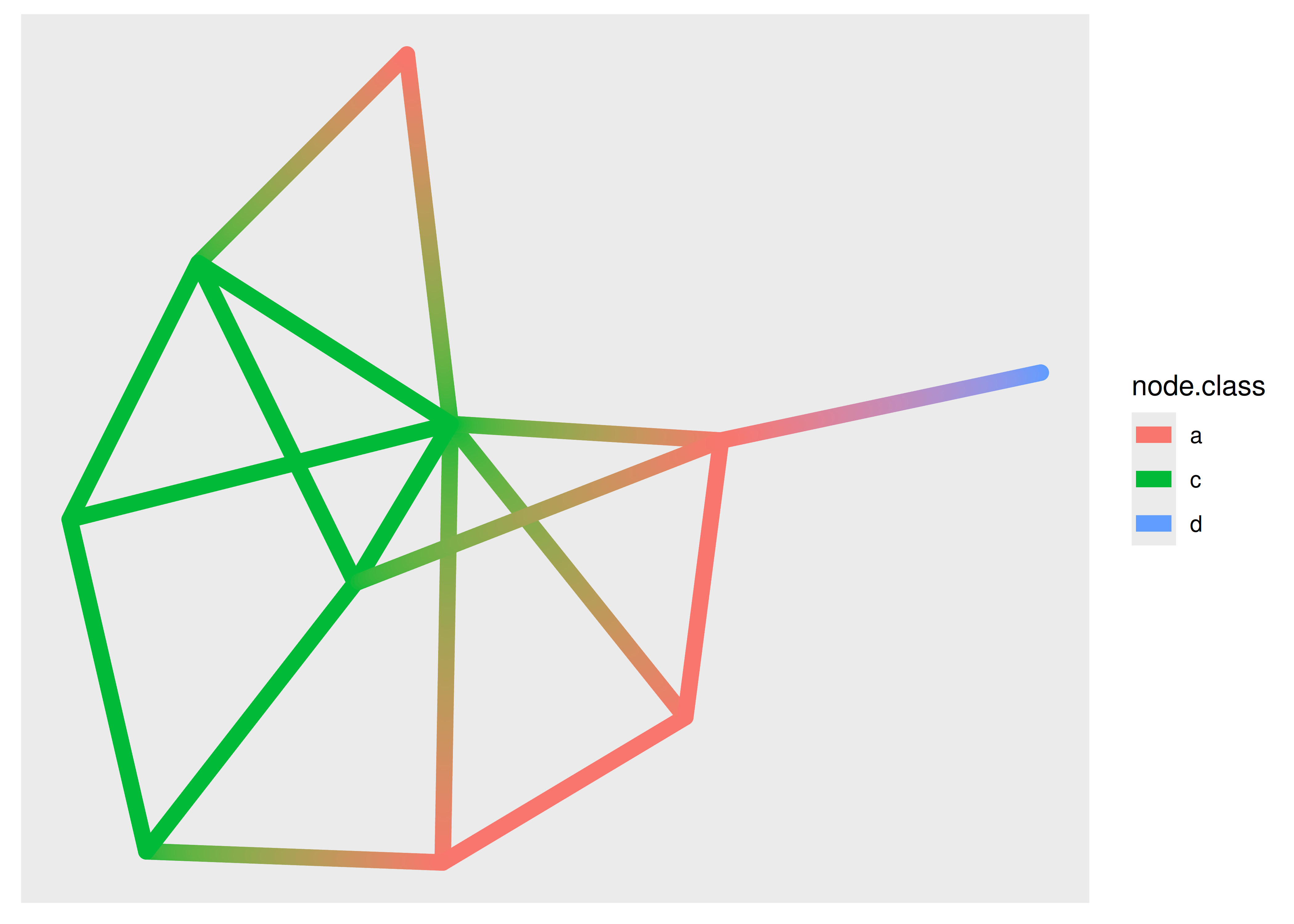
El uso de la variable node.class puede sorprenderte. Las geoms de borde tienen acceso a las variables de los nodos terminales a través de variables con prefijos especiales. Para las versiones estándar y 0, están disponibles a través de las variables con prefijo node1. y node2., y para la versión 2, están disponibles a través de las variables con prefijo node. (como se usó anteriormente). Las tres versiones de geoms de borde son comunes a todos los tipos de geoms de borde, no solo a geom_edge_link().
Hay más formas de dibujar bordes que simples líneas rectas. Algunos son específicos de árboles o diseños específicos, pero muchos son de uso general. Un caso de uso específico para otro tipo de borde es cuando hay múltiples bordes entre los mismos nodos. Dibujarlos como líneas rectas oscurecerá la multiplicidad de los bordes, que es, por ejemplo, evidente con el gráfico de la escuela secundaria donde están presentes múltiples bordes paralelos pero invisibles en los gráficos anteriores. Para mostrar bordes paralelos, puede usar geom_edge_fan() o geom_edge_parallel():
ggraph(hs_graph, layout = "stress") +
geom_edge_fan()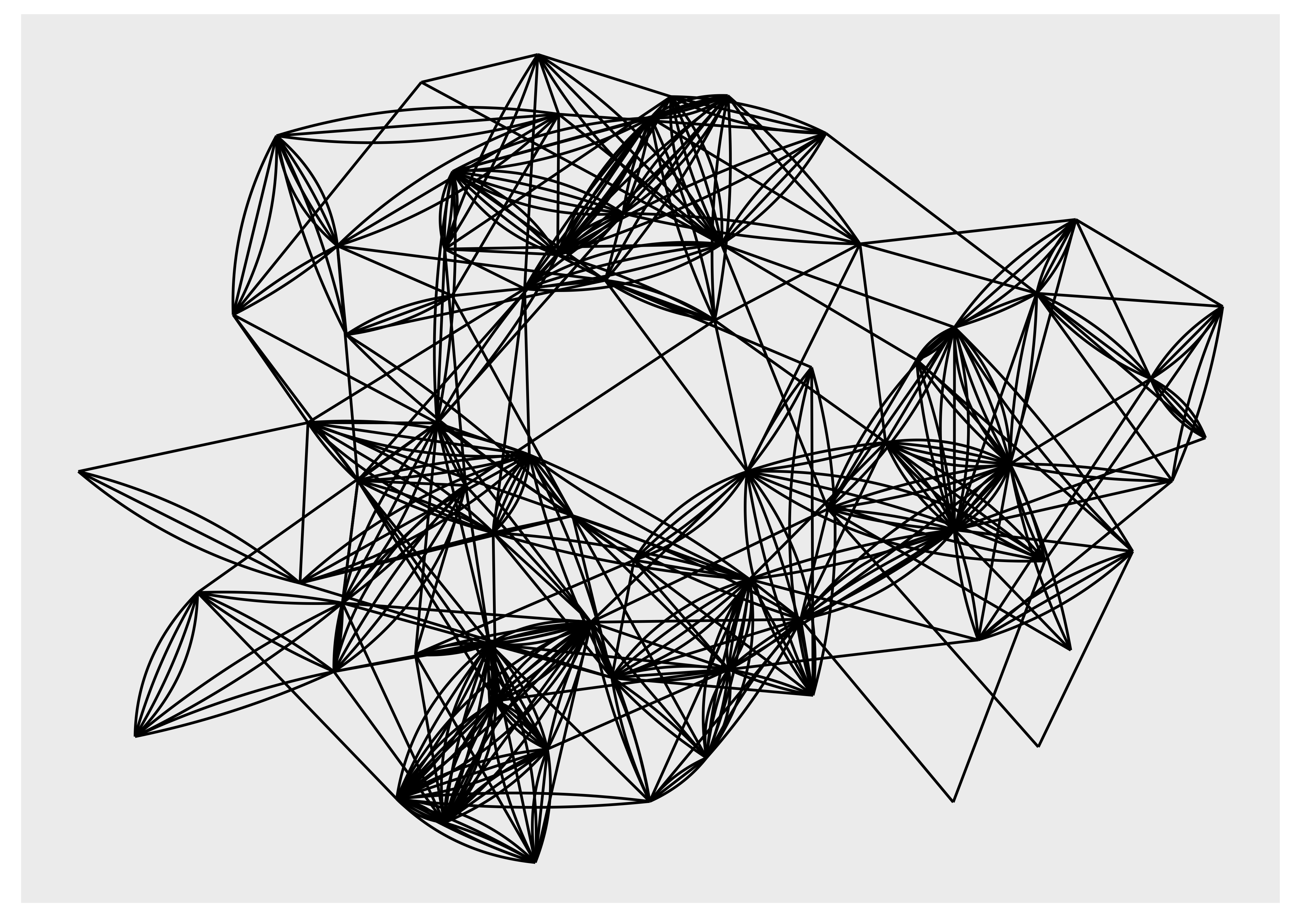
ggraph(hs_graph, layout = "stress") +
geom_edge_parallel()
Está claro que estas geoms sólo deben usarse para gráficos relativamente simples, ya que aumentan la cantidad de desorden y sobretrazado en el gráfico. Al observar los árboles y específicamente los dendrogramas, un tipo de borde comúnmente utilizado es el borde del codo:
ggraph(luv_graph, layout = "dendrogram", height = height) +
geom_edge_elbow()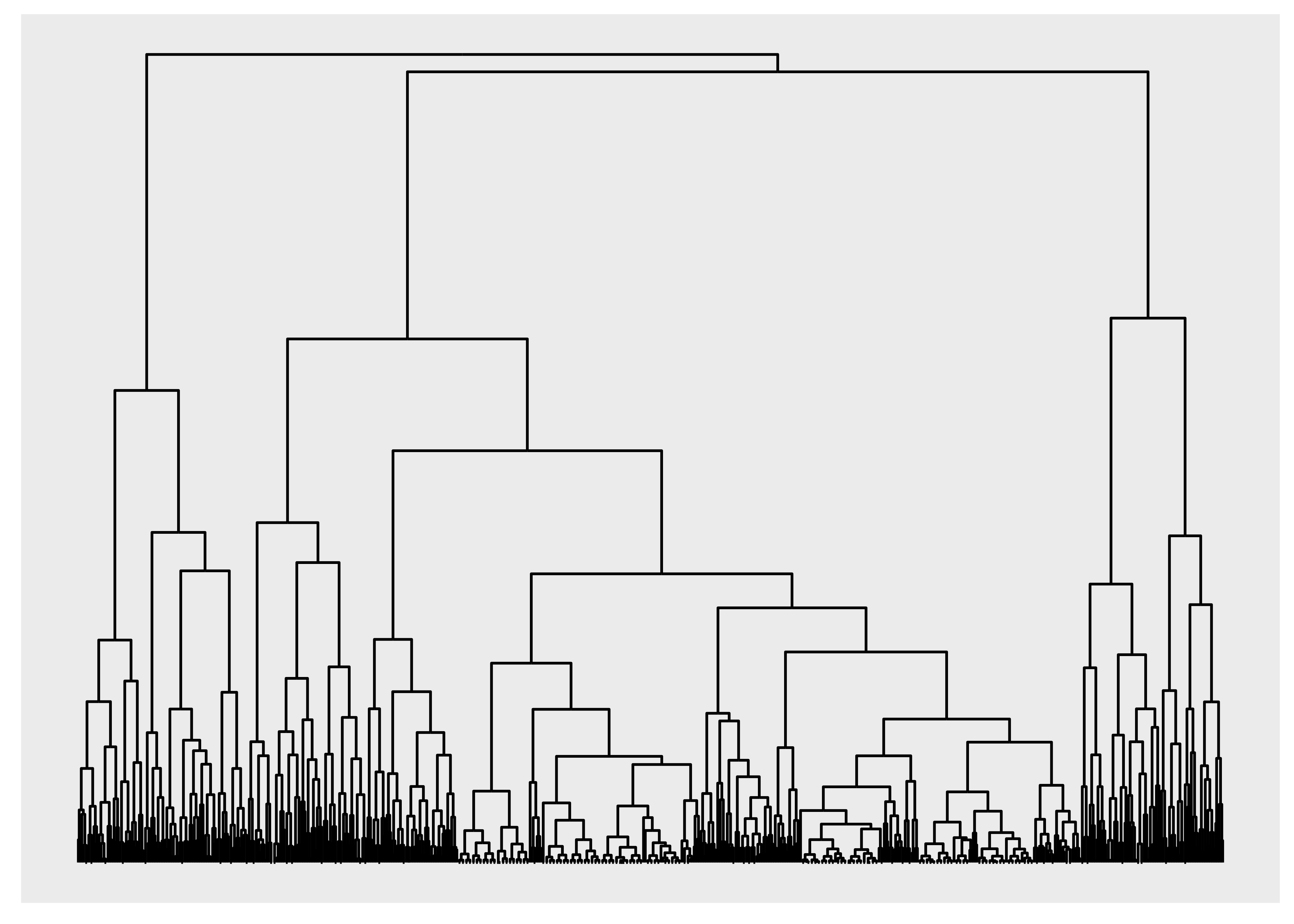
geom_edge_bend() y geom_edge_diagonal() son versiones más suaves de esto.
7.2.3.1 Recortar bordes alrededor de los nodos.
Un problema común, especialmente cuando se utilizan flechas para mostrar la direccionalidad de los bordes, es que el nodo se superpondrá al borde porque corre hacia el centro del nodo, no hacia el borde del punto que muestra el nodo. Esto se puede ver a continuación:
ggraph(graph, layout = "stress") +
geom_edge_link(arrow = arrow()) +
geom_node_point(aes(colour = class), size = 8)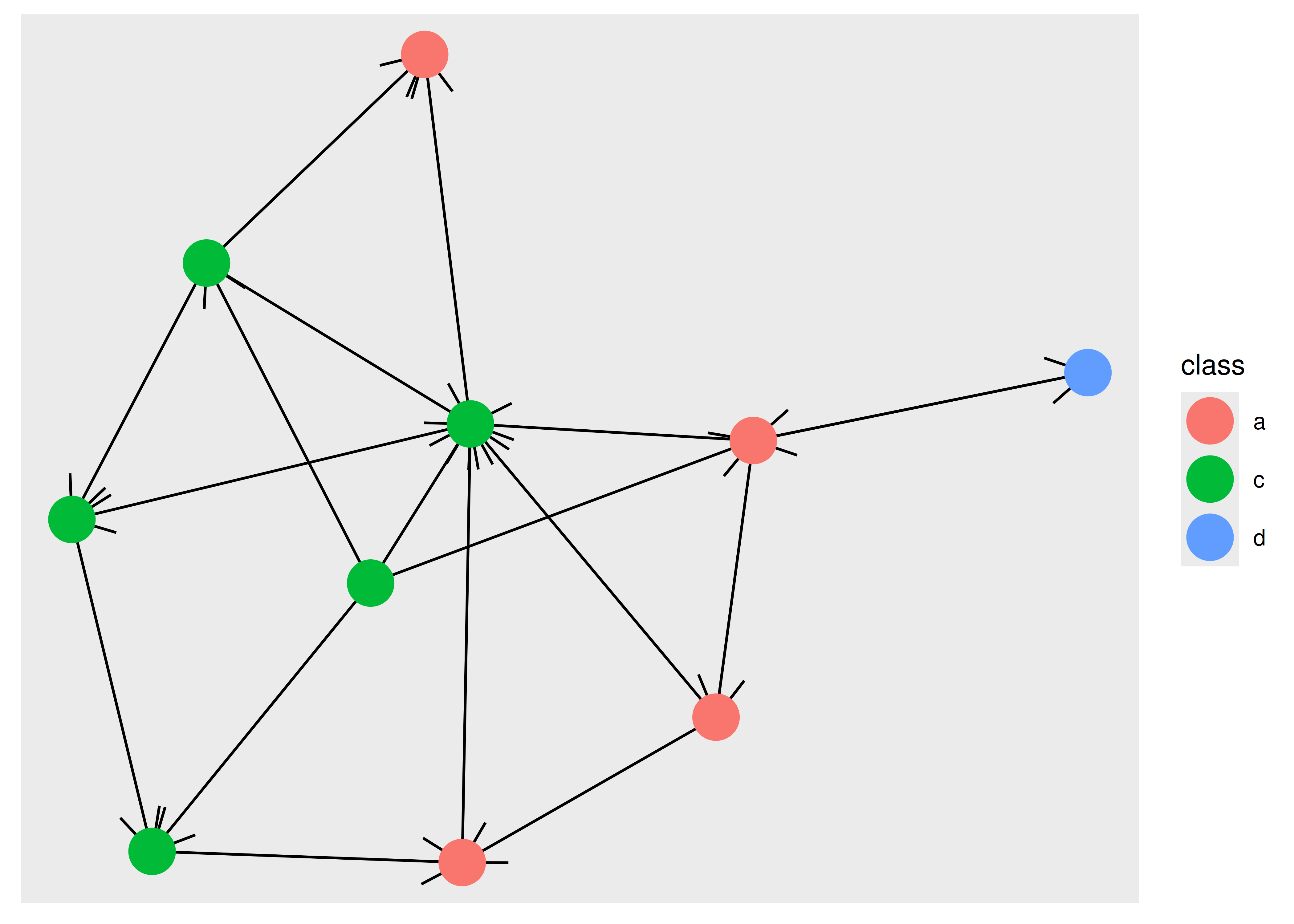
Obviamente, nos gustaría que los bordes se detuvieran antes de llegar al punto para que la flecha no quede oculta. Esto es posible en ggraph usando la estética start_cap y end_cap que le permiten especificar una región de recorte alrededor de los nodos terminales. Para arreglar el gráfico anterior, estableceríamos una región de recorte circular del tamaño correcto alrededor de cada nodo:
ggraph(graph, layout = "stress") +
geom_edge_link(
arrow = arrow(),
start_cap = circle(5, "mm"),
end_cap = circle(5, "mm")
) +
geom_node_point(aes(colour = class), size = 8)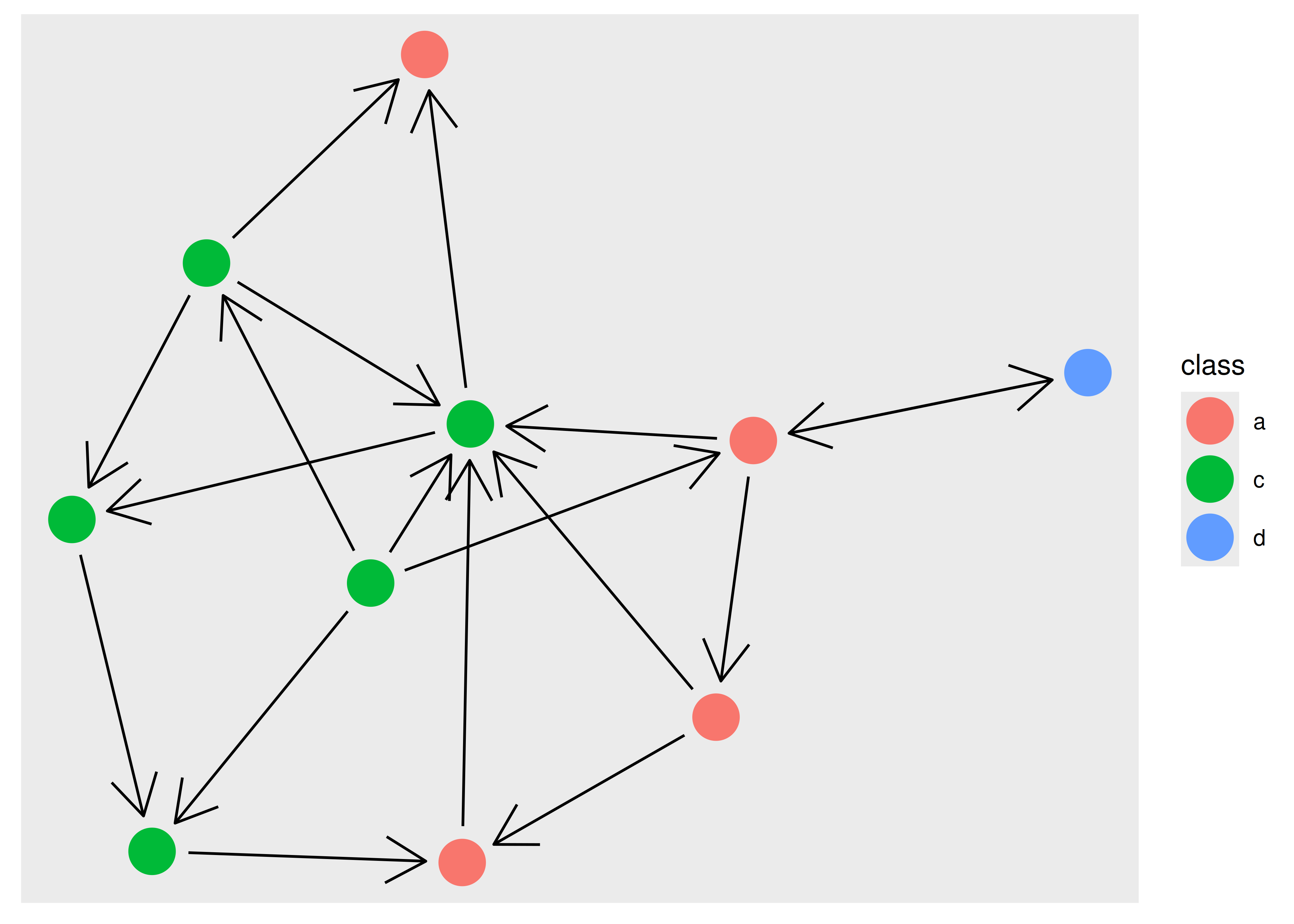
7.2.3.2 Un borde no siempre es una línea
Si bien es natural pensar en los bordes como diferentes tipos de líneas que conectan puntos, esto sólo es cierto para ciertos tipos de trazados de red. Siempre hay que tener en cuenta que los nodos y los bordes son conceptos abstractos y se pueden visualizar de multitud de formas. Como ejemplo de esto, podemos observar los gráficos matriciales que muestran nodos implícitamente por posición de fila y columna, y muestran los bordes como puntos o mosaicos.
ggraph(hs_graph, layout = "matrix", sort.by = node_rank_traveller()) +
geom_edge_point()
7.2.4 Facetado
El facetado no es un concepto que se aplica frecuentemente a la visualización de redes, pero es tan poderoso para redes como lo es para datos tabulares. Si bien las funciones de facetado estándar en ggplot2 funcionan técnicamente con ggraph, no lo hacen a nivel conceptual, ya que los nodos y los bordes están conectados y dividir los nodos en múltiples subtramas moverá automáticamente los bordes con ellos, aunque los bordes no tengan la variable de facetado en sus datos. Debido a esto, ggraph proporciona sus propias versiones especializadas de facet_wrap() y facet_grid(). facet_nodes() y facet_edges() apuntarán a nodos o bordes y envolverán los paneles de la misma manera que facet_wrap(). Para facet_nodes() la convención es que si un borde va entre dos nodos en el mismo panel, se mostrará en ese panel, pero si se divide entre varios paneles, se eliminará. Para facet_edges() los nodos se repetirán en todos los paneles. Para verlo en acción podemos mirar el gráfico de nuestra escuela secundaria y ver cómo han evolucionado sus amistades a lo largo de los años.
ggraph(hs_graph, layout = "stress") +
geom_edge_link() +
geom_node_point() +
facet_edges(~year)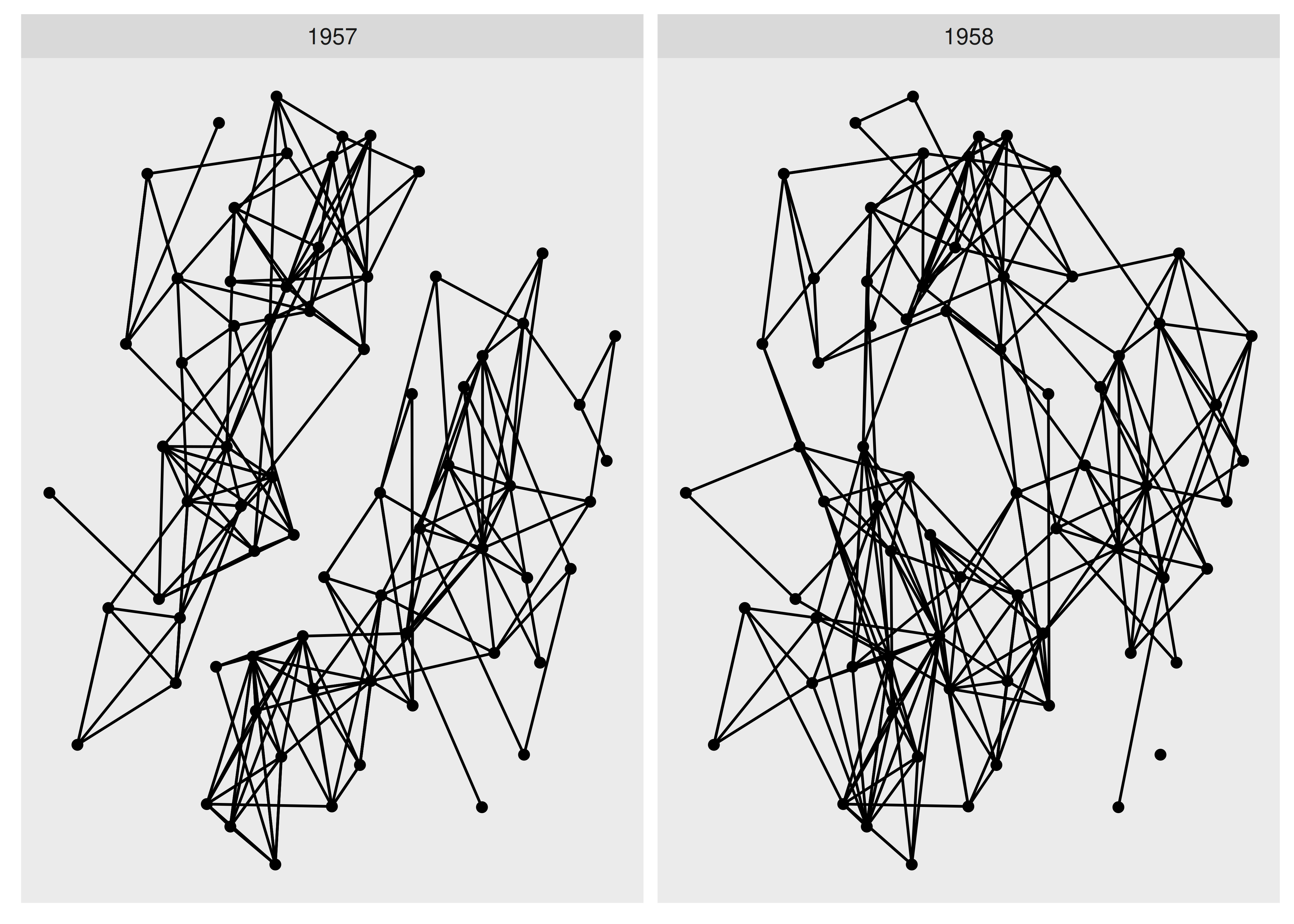
Como queda muy claro con el facetado, vemos una clara evolución de las amistades que van de dos grupos completamente separados a un solo grupo más mixto.
Como el facetado también acepta algoritmos de tidygraph, es una excelente manera de evaluar, p. el resultado de agrupaciones sobre la marcha.
ggraph(hs_graph, layout = "stress") +
geom_edge_link() +
geom_node_point() +
facet_nodes(~ group_spinglass())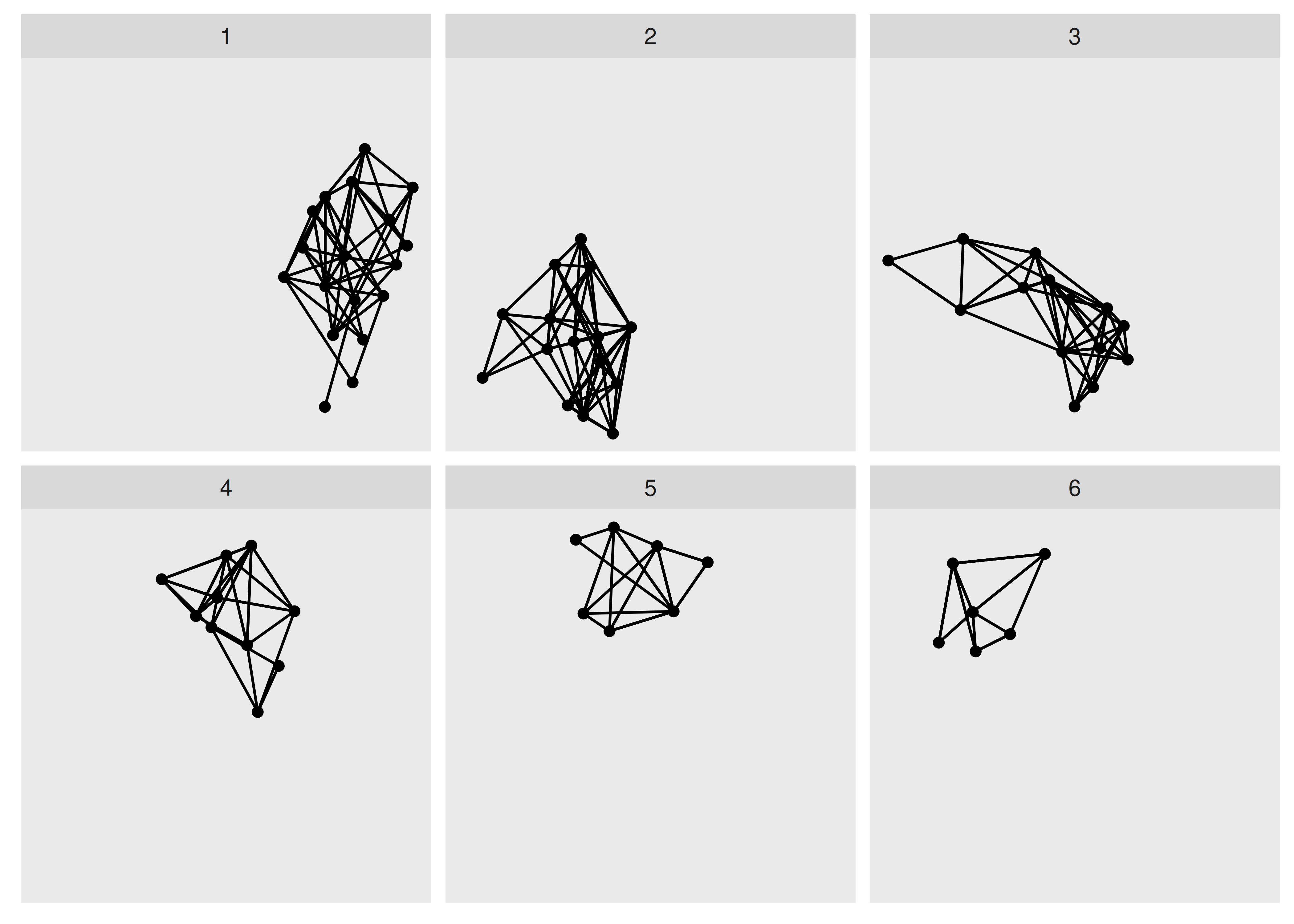
El último tipo de faceta incluido es facet_graph() que funciona como facet_grid(), pero le permite especificar en qué parte deben facetarse las filas y columnas, bordes o nodos.
7.3 ¿Quieren más?
Esto es sólo una muestra de las posibilidades presentadas en ggraph. Si desea profundizar más, puede encontrar útiles los recursos en https://tidygraph.data-imaginist.com y https://ggraph.data-imaginist.com. Comprender los fundamentos de tidygraph y la API aumentará su dominio y comprensión de ggraph, así que asegúrese de estudiarlos al unísono.