13 Construya una gráfica capa por capa

You are reading the work-in-progress third edition of the ggplot2 book. This chapter is currently a dumping ground for ideas, and we don’t recommend reading it.

13.1 Introducción

Una de las ideas clave detrás de ggplot2 es que le permite iterar fácilmente, construyendo un gráfico complejo capa por capa. Cada capa puede provenir de un conjunto de datos diferente y tener un mapeo estético diferente, lo que permite crear gráficos sofisticados que muestran datos de múltiples fuentes.

Ya has creado capas con funciones como geom_point() y geom_histogram(). En este capítulo, profundizará en los detalles de una capa y en cómo puede controlar los cinco componentes: datos, asignaciones estéticas, geom, estadísticas y ajustes de posición. El objetivo aquí es brindarle las herramientas para crear gráficos sofisticados adaptados al problema en cuestión.

13.2 Construyendo una gráfica

Hasta ahora, cada vez que creamos un gráfico con ggplot(), inmediatamente agregamos una capa con una función geom. Pero es importante darse cuenta de que en realidad hay dos pasos distintos. Primero, creamos un gráfico con un conjunto de datos predeterminado y asignaciones estéticas:

p <- ggplot(mpg, aes(displ, hwy))
p

No hay nada que ver todavía, así que necesitamos agregar una capa:

p + geom_point()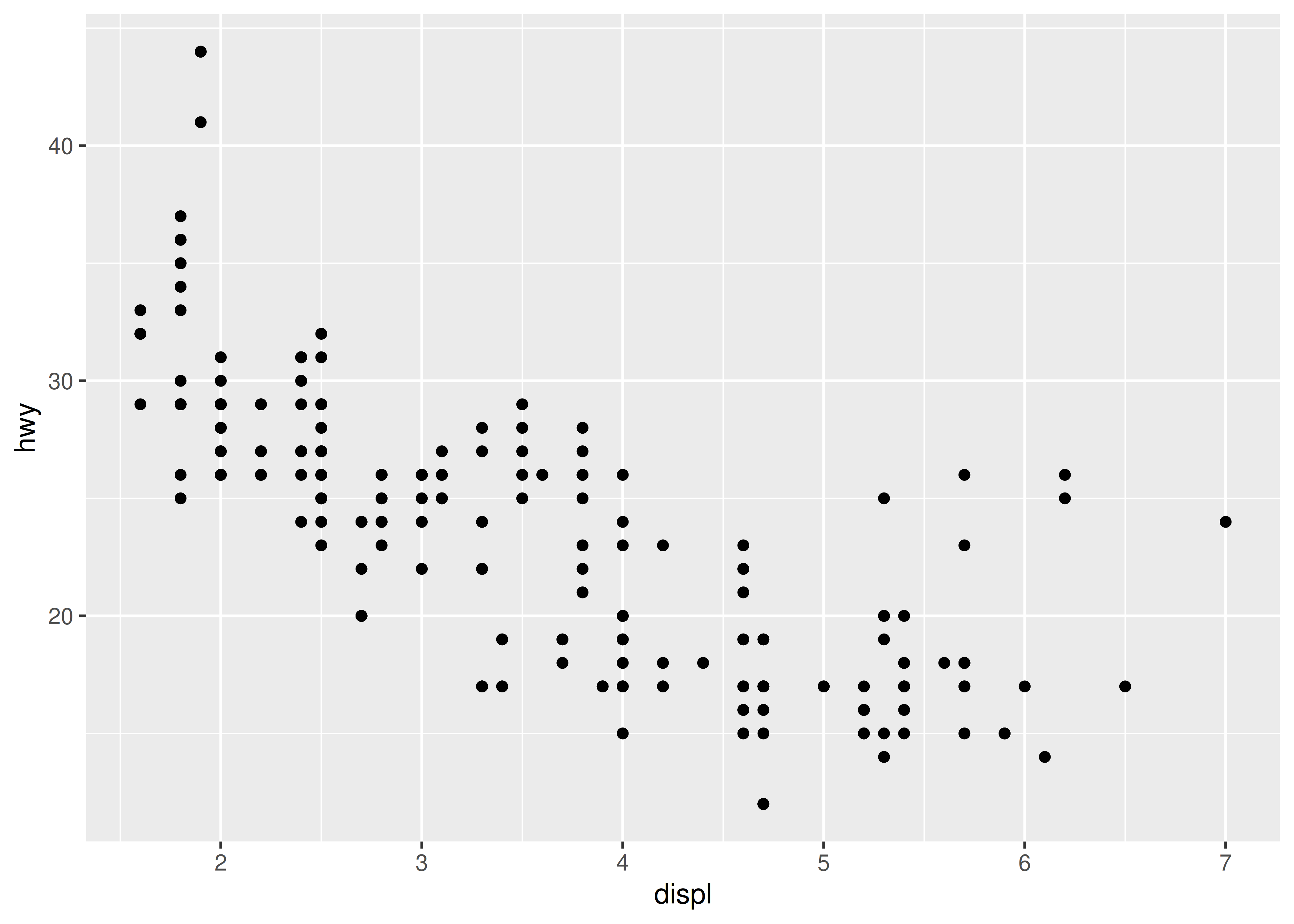

geom_point() es un atajo. Detrás de escena, llama a la función layer() para crear una nueva capa:

p + layer(
  mapping = NULL, 
  data = NULL,
  geom = "point", 
  stat = "identity",
  position = "identity"
)

Esta llamada especifica completamente los cinco componentes de la capa:

mapping: Un conjunto de asignaciones estéticas, especificadas mediante la función aes() y combinadas con los valores predeterminados de la gráfica como se describe en Sección 13.4. Si es NULL, utiliza la asignación predeterminada establecida en ggplot().
data: Un conjunto de datos que anula el conjunto de datos de trazado predeterminado. Generalmente se omite (establecido en NULL), en cuyo caso la capa utilizará los datos predeterminados especificados en ggplot(). Los requisitos de datos se explican con más detalle en Sección 13.3.
geom: El nombre del objeto geométrico que se utilizará para dibujar cada observación. Las geoms se analizan con más detalle en Sección 13.3, y Capítulo 3 y Capítulo 4 exploran su uso con más profundidad.

Las geoms pueden tener argumentos adicionales. Todas las geoms toman la estética como parámetro. Si proporciona una estética (por ejemplo, color) como parámetro, no se escalará, lo que le permitirá controlar la apariencia del gráfico, como se describe en Sección 13.4.2. Puede pasar parámetros en ... (en cuyo caso los parámetros stat y geom se separan automáticamente), o en una lista pasada a geom_params.
stat: El nombre de la transformación estadística a utilizar. Una transformación estadística realiza un resumen estadístico útil y es clave para histogramas y suavizadores. Para mantener los datos tal como están, utilice la estadística de “identidad”. Obtenga más información en Sección 13.6.

Solo necesita configurar una estadística y una geom: cada geom tiene una estadística predeterminada y cada estadística una geom predeterminada.

La mayoría de las estadísticas toman parámetros adicionales para especificar los detalles de la transformación estadística. Puede proporcionar parámetros en ... (en cuyo caso los parámetros stat y geom se separan automáticamente) o en una lista llamada stat_params.
position: El método utilizado para ajustar objetos superpuestos, como vibrar, apilar o esquivar. Más detalles en Sección 13.7.

Es útil comprender la función layer() para tener un mejor modelo mental del objeto de capa. Pero rara vez utilizarás la llamada layer() completa porque es muy detallada. En su lugar, usarás las funciones de acceso directo geom_: geom_point(mapping, data, ...) es exactamente equivalente a layer(mapping, data, geom = "point", ...).

13.3 Datos

Cada capa debe tener algunos datos asociados y esos datos deben estar en un marco de datos ordenado. Los marcos de datos ordenados se describen con más detalle en R para ciencia de datos (https://r4ds.had.co.nz), pero por ahora, todo lo que necesita saber es que un marco de datos ordenado tiene variables en las columnas y observaciones en las filas. Esta es una restricción fuerte, pero hay buenas razones para ello:

Tus datos son muy importantes, por eso lo mejor es ser explícito al respecto.
Un único marco de datos también es más fácil de guardar que una multitud de vectores, lo que significa que es más fácil reproducir los resultados o enviar los datos a otra persona.
Impone una clara separación de preocupaciones: ggplot2 convierte los marcos de datos en visualizaciones. Otros paquetes pueden crear marcos de datos en el formato correcto.

No es necesario que los datos de cada capa sean los mismos y, a menudo, resulta útil combinar varios conjuntos de datos en un solo gráfico. Para ilustrar esa idea, generaremos dos nuevos conjuntos de datos relacionados con el conjunto de datos de mpg. Primero, ajustaremos un modelo loess y generaremos predicciones a partir de él. (Esto es lo que geom_smooth() hace detrás de escena)

mod <- loess(hwy ~ displ, data = mpg)
grid <- tibble(displ = seq(min(mpg$displ), max(mpg$displ), length = 50))
grid$hwy <- predict(mod, newdata = grid)

grid
#> # A tibble: 50 × 2
#>   displ   hwy
#>   <dbl> <dbl>
#> 1  1.6   33.1
#> 2  1.71  32.2
#> 3  1.82  31.3
#> 4  1.93  30.4
#> 5  2.04  29.6
#> 6  2.15  28.8
#> # ℹ 44 more rows

A continuación, aislaremos las observaciones que están particularmente alejadas de sus valores previstos:

std_resid <- resid(mod) / mod$s
outlier <- filter(mpg, abs(std_resid) > 2)
outlier
#> # A tibble: 6 × 11
#>   manufacturer model      displ  year   cyl trans  drv     cty   hwy fl    class
#>   <chr>        <chr>      <dbl> <int> <int> <chr>  <chr> <int> <int> <chr> <chr>
#> 1 chevrolet    corvette     5.7  1999     8 manua… r        16    26 p     2sea…
#> 2 pontiac      grand prix   3.8  2008     6 auto(… f        18    28 r     mids…
#> 3 pontiac      grand prix   5.3  2008     8 auto(… f        16    25 p     mids…
#> 4 volkswagen   jetta        1.9  1999     4 manua… f        33    44 d     comp…
#> 5 volkswagen   new beetle   1.9  1999     4 manua… f        35    44 d     subc…
#> 6 volkswagen   new beetle   1.9  1999     4 auto(… f        29    41 d     subc…

Hemos generado estos conjuntos de datos porque es común mejorar la visualización de datos sin procesar con un resumen estadístico y algunas anotaciones. Con estos nuevos conjuntos de datos, podemos mejorar nuestro diagrama de dispersión inicial superponiendo una línea suavizada y etiquetando los puntos periféricos:

ggplot(mpg, aes(displ, hwy)) + 
  geom_point() + 
  geom_line(data = grid, colour = "blue", linewidth = 1.5) +
  geom_text(data = outlier, aes(label = model))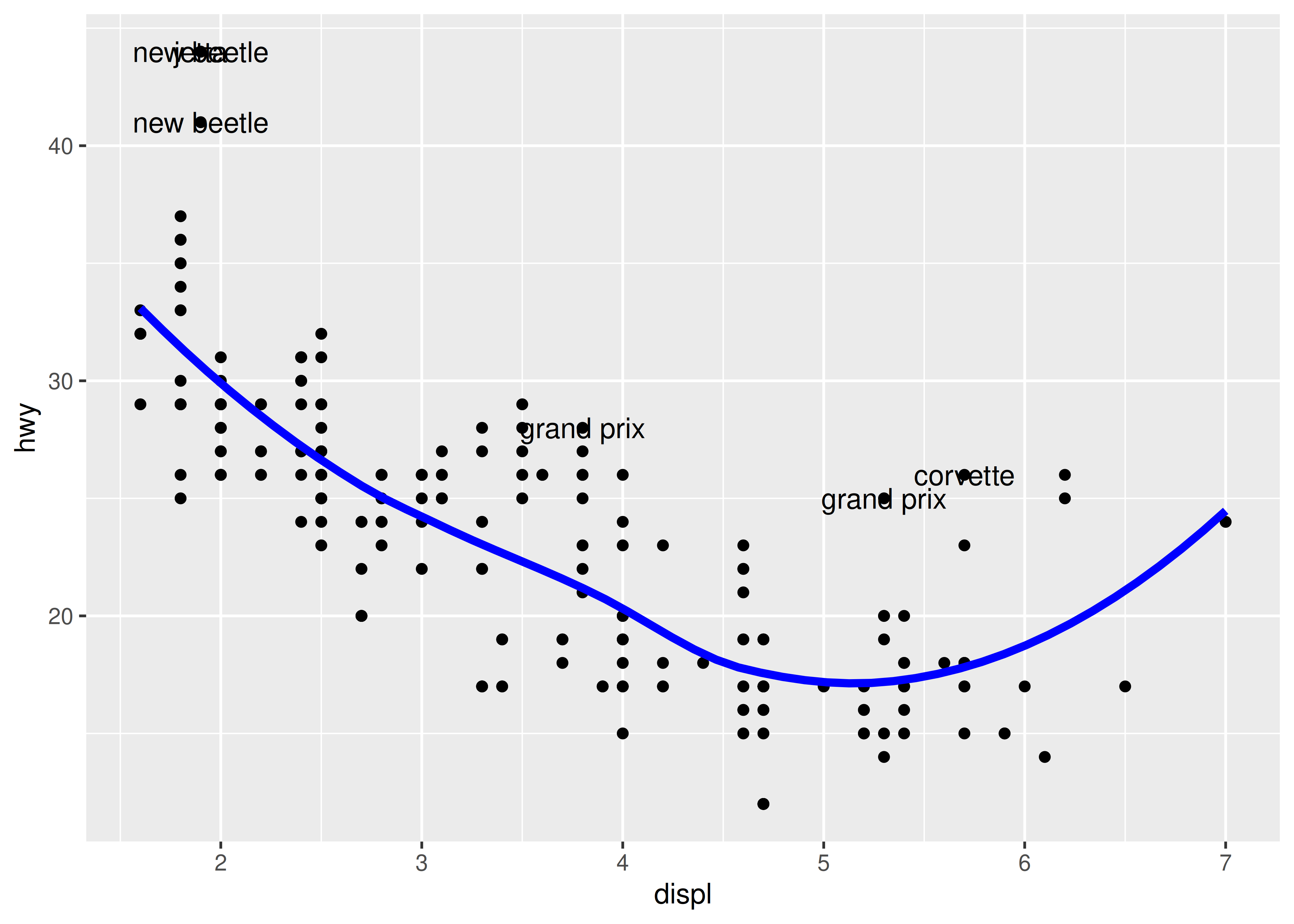

(Las etiquetas no son particularmente fáciles de leer, pero puedes solucionarlo con algunos ajustes manuales).

Tenga en cuenta que necesita el data = explícito en las capas, pero no en la llamada a ggplot(). Esto se debe a que el orden de los argumentos es diferente. Esto es un poco inconsistente, pero reduce la escritura en el caso común en el que especificas los datos una vez en ggplot() y modificas la estética en cada capa.

En este ejemplo, cada capa utiliza un conjunto de datos diferente. Podríamos definir el mismo gráfico de otra manera, omitiendo el conjunto de datos predeterminado y especificando un conjunto de datos para cada capa:

ggplot(mapping = aes(displ, hwy)) + 
  geom_point(data = mpg) + 
  geom_line(data = grid) + 
  geom_text(data = outlier, aes(label = model))

No nos gusta particularmente este estilo en este ejemplo porque deja menos claro cuál es el conjunto de datos principal (y debido a la forma en que están ordenados los argumentos de ggplot(), en realidad requiere más pulsaciones de teclas). Sin embargo, es posible que lo prefiera en los casos en los que no haya un conjunto de datos primario claro o en los que la estética también varíe de una capa a otra.

13.3.1 Ejercicios

Los dos primeros argumentos de ggplot son “datos” y “mapeo”. Los dos primeros argumentos de todas las funciones de capa son “mapeo” y “datos”. ¿Por qué difiere el orden de los argumentos? (Sugerencia: piense en lo que configura con más frecuencia).
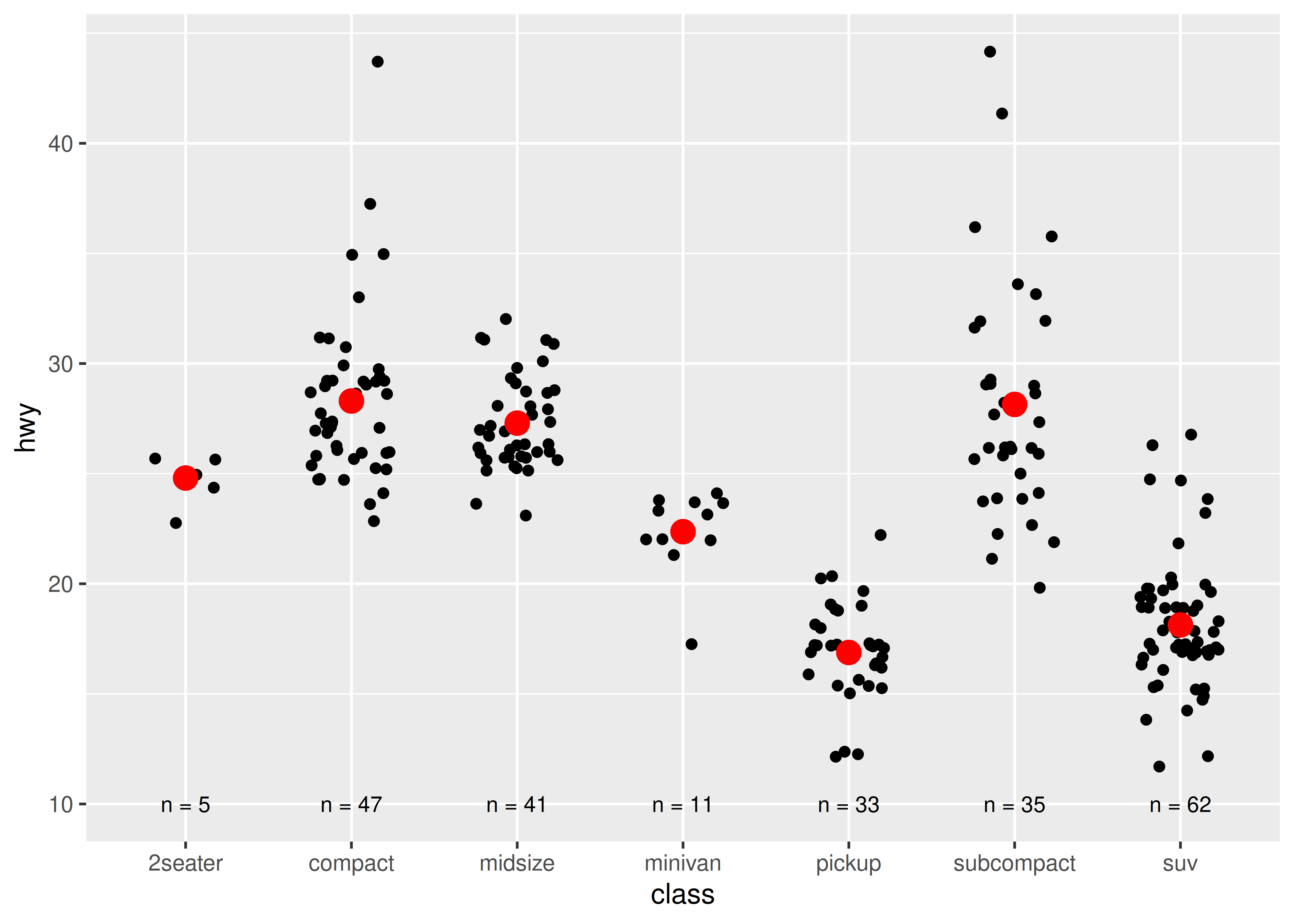
El siguiente código utiliza dplyr para generar algunas estadísticas resumidas sobre cada clase de automóvil.
```
library(dplyr)
class <- mpg %>% 
  group_by(class) %>% 
  summarise(n = n(), hwy = mean(hwy))
```
Utilice los datos para recrear esta gráfica:

13.4 Mapeos estéticos

Las asignaciones estéticas, definidas con aes(), describen cómo se asignan las variables a propiedades visuales o estética. aes() toma una secuencia de pares de variables estéticas como esta:

aes(x = displ, y = hwy, colour = class)

(Si eres estadounidense, puedes usar color, y detrás de escena ggplot2 corregirá tu ortografía;)

Aquí asignamos la posición x a displ, la posición y a hwy y el color a class. Los nombres de los dos primeros argumentos se pueden omitir, en cuyo caso corresponden a las variables x e y. Eso hace que esta especificación sea equivalente a la anterior:

aes(displ, hwy, colour = class)

Si bien puedes manipular datos en aes(), p. aes(log(carat), log(price)), es mejor hacer sólo cálculos simples. Es mejor mover transformaciones complejas fuera de la llamada aes() y llevarlas a una llamada explícita dplyr::mutate(). Esto hace que sea más fácil verificar tu trabajo y, a menudo, es más rápido porque solo necesitas hacer la transformación una vez, no cada vez que se dibuja la gráfica.

Nunca haga referencia a una variable con $ (por ejemplo, diamondss$carat) en aes(). Esto rompe la contención, de modo que el gráfico ya no contiene todo lo que necesita y causa problemas si ggplot2 cambia el orden de las filas, como lo hace al facetar.

13.4.1 Especificando la estética en la gráfica versus en las capas.

Los mapeos estéticos se pueden proporcionar en la llamada inicial a ggplot(), en capas individuales o en alguna combinación de ambas. Todas estas llamadas crean la misma especificación de gráfica:

ggplot(mpg, aes(displ, hwy, colour = class)) + 
  geom_point()
ggplot(mpg, aes(displ, hwy)) + 
  geom_point(aes(colour = class))
ggplot(mpg, aes(displ)) + 
  geom_point(aes(y = hwy, colour = class))
ggplot(mpg) + 
  geom_point(aes(displ, hwy, colour = class))

Dentro de cada capa, puede agregar, anular o eliminar asignaciones. Por ejemplo, si tiene un gráfico que utiliza los datos mpg que tiene aes(displ, hwy) como punto de partida, la siguiente tabla ilustra las tres operaciones:

Operación | Estética de capas | Resultado |

Si solo tiene una capa en el trazado, la forma en que especifique la estética no hace ninguna diferencia. Sin embargo, la distinción es importante cuando empiezas a agregar capas adicionales. Estos dos gráficos son válidos e interesantes, pero se centran en bastantes aspectos diferentes de los datos:

ggplot(mpg, aes(displ, hwy, colour = class)) + 
  geom_point() + 
  geom_smooth(method = "lm", se = FALSE) +
  theme(legend.position = "none")
#> `geom_smooth()` using formula = 'y ~ x'

ggplot(mpg, aes(displ, hwy)) + 
  geom_point(aes(colour = class)) + 
  geom_smooth(method = "lm", se = FALSE) + 
  theme(legend.position = "none")
#> `geom_smooth()` using formula = 'y ~ x'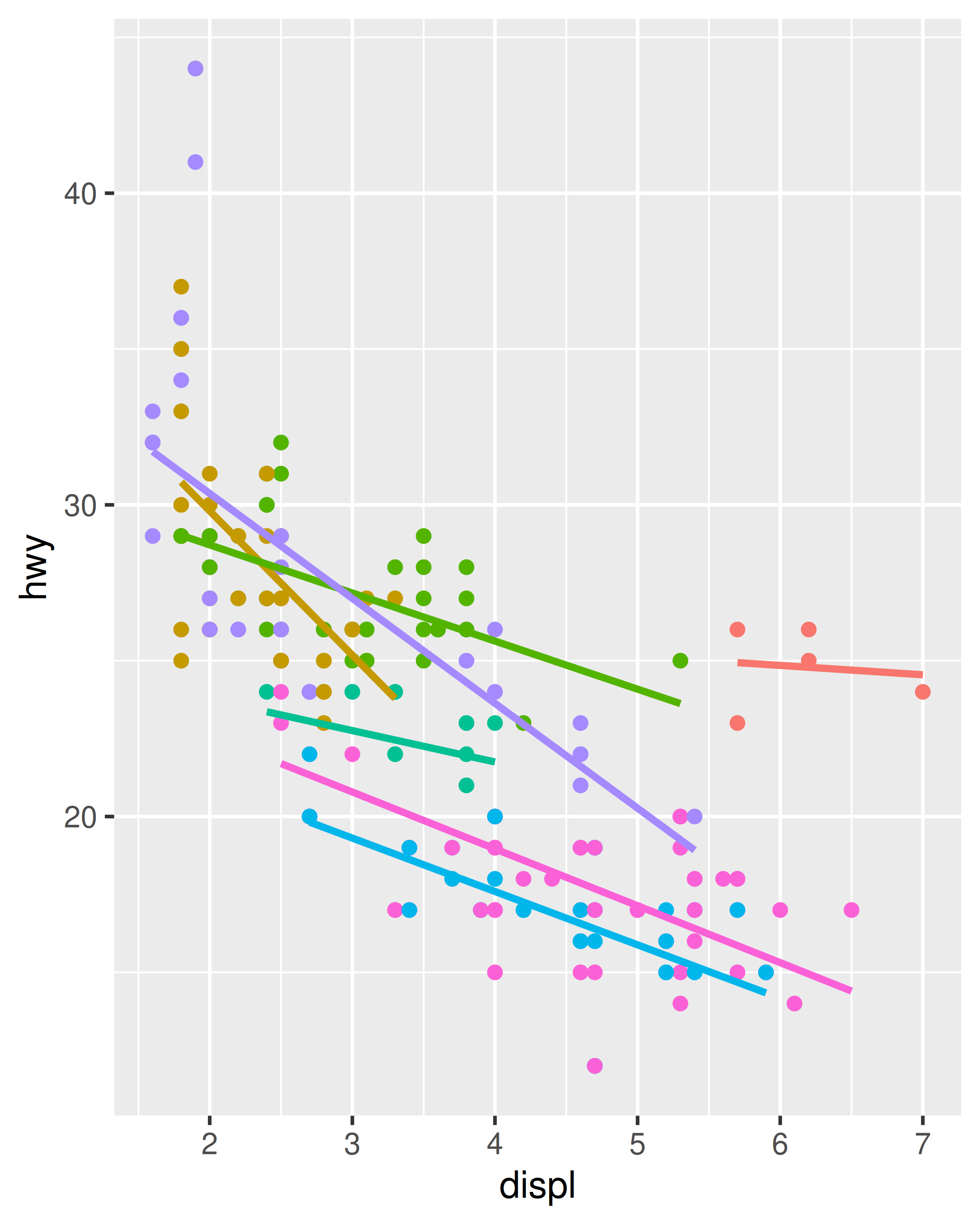

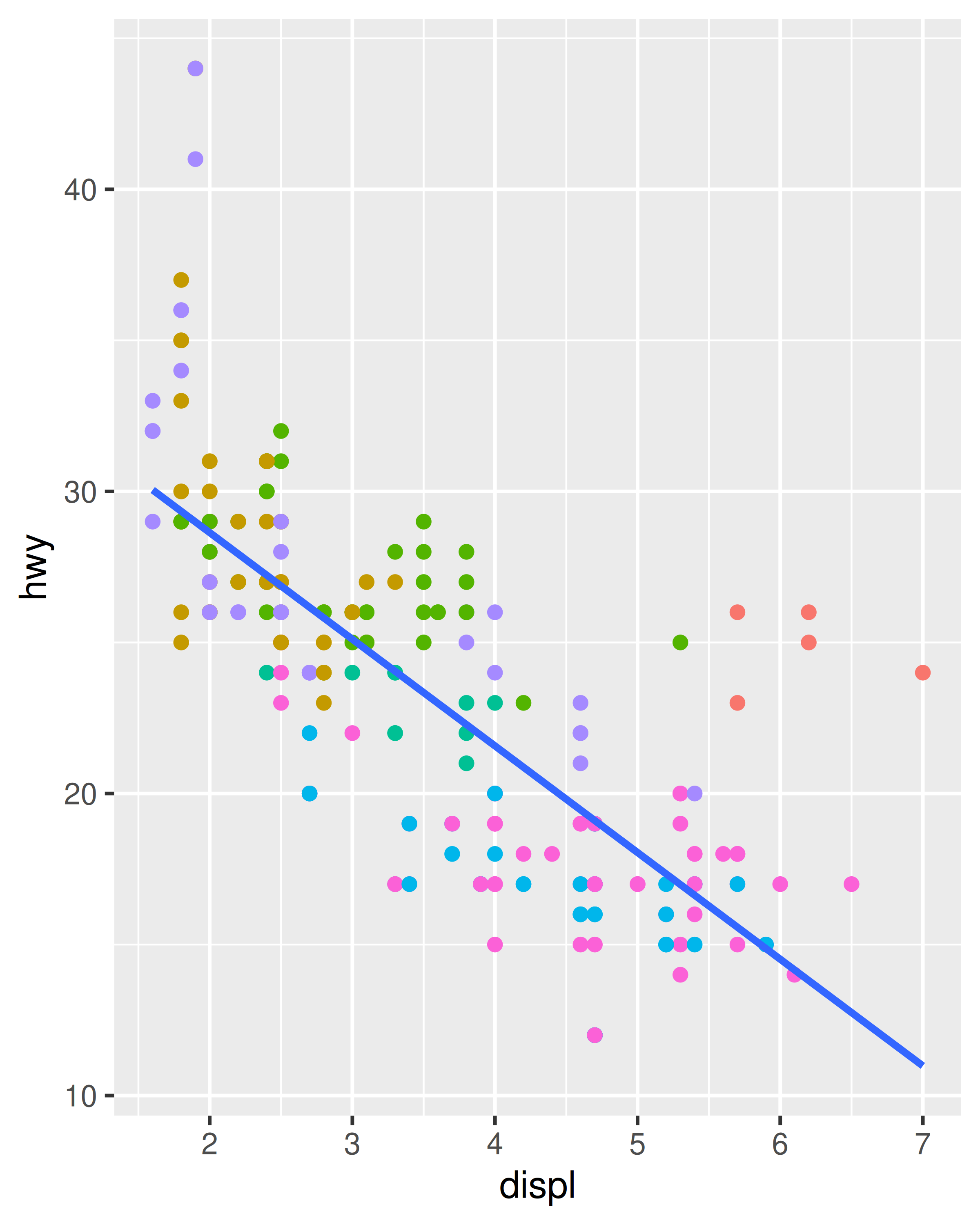
Generalmente, desea configurar las asignaciones para iluminar la estructura subyacente al gráfico y minimizar la escritura. Puede pasar algún tiempo antes de que el mejor enfoque sea inmediatamente obvio, por lo que si ha iterado hasta llegar a un gráfico complejo, puede que valga la pena reescribirlo para que la estructura sea más clara.

13.4.2 Configuración versus mapeo

En lugar de asignar una propiedad estética a una variable, puede establecerla en un valor único especificándolo en los parámetros de la capa. Asignamos una estética a una variable (p. ej., aes(colour = cut)) o la establecemos en una constante (p. ej., colour = "red"). Si desea que la apariencia esté gobernada por una variable, coloque la especificación dentro de aes(); Si desea anular el tamaño o color predeterminado, coloque el valor fuera de aes().

Los siguientes gráficos se crean con código similar, pero tienen resultados bastante diferentes. El segundo gráfico asigna (no establece) el color al valor ‘darkblue’. Esto crea efectivamente una nueva variable que contiene solo el valor ‘darkblue’ y luego la escala con una escala de colores. Debido a que este valor es discreto, la escala de colores predeterminada utiliza colores espaciados uniformemente en la rueda de colores y, como solo hay un valor, este color es rosado.

ggplot(mpg, aes(cty, hwy)) + 
  geom_point(colour = "darkblue") 

ggplot(mpg, aes(cty, hwy)) + 
  geom_point(aes(colour = "darkblue"))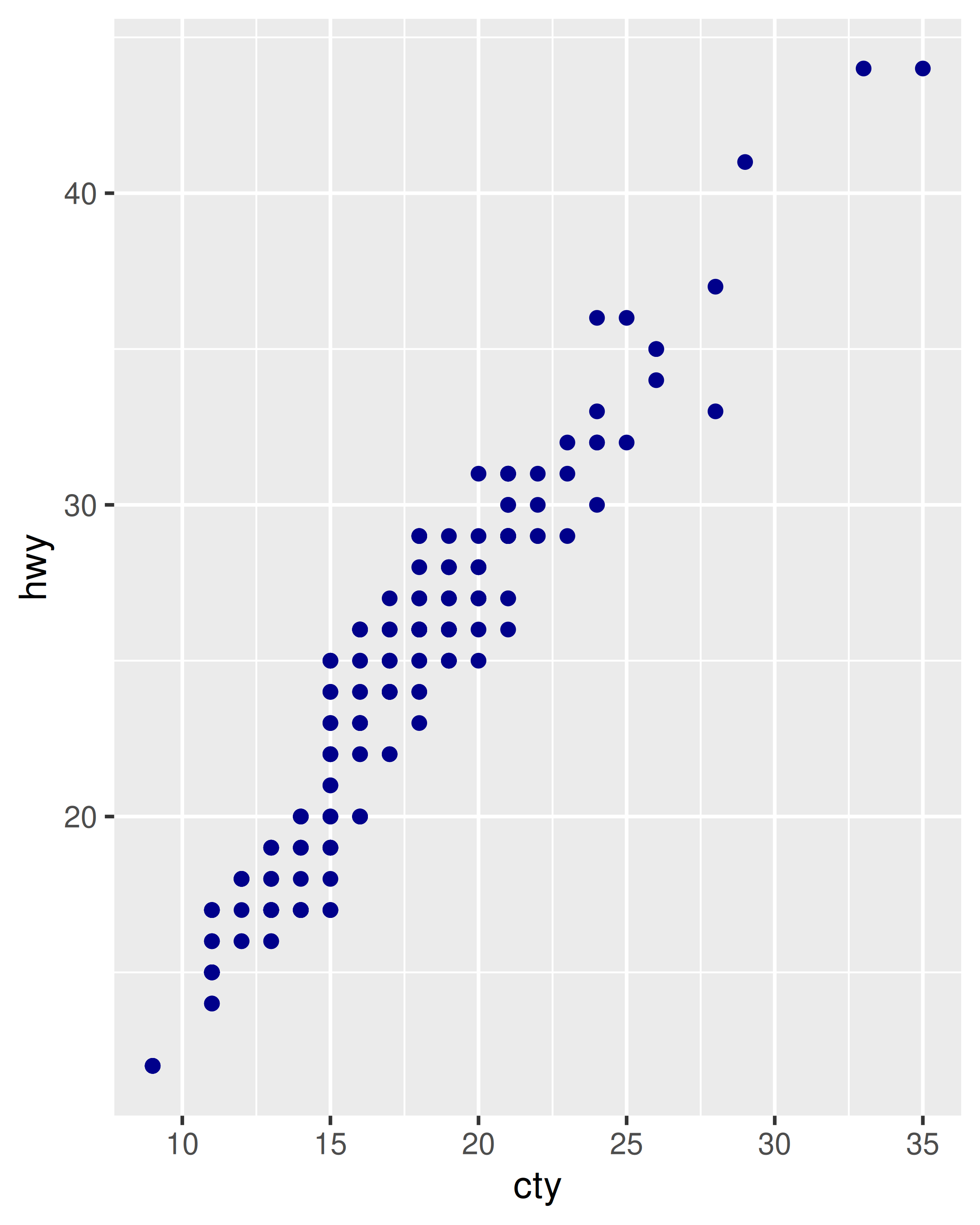

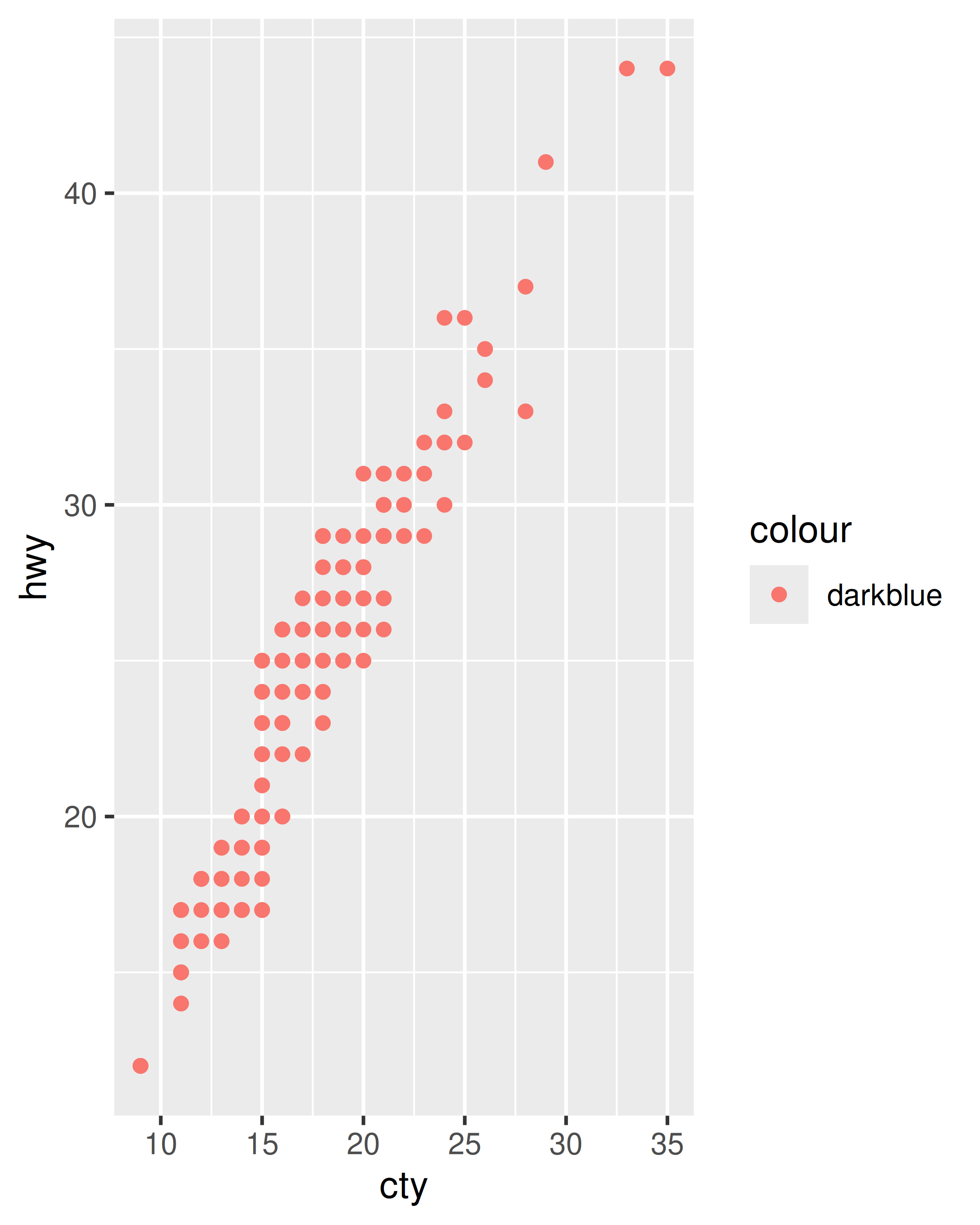
Un tercer enfoque consiste en asignar el valor, pero anular la escala predeterminada:

ggplot(mpg, aes(cty, hwy)) + 
  geom_point(aes(colour = "darkblue")) + 
  scale_colour_identity()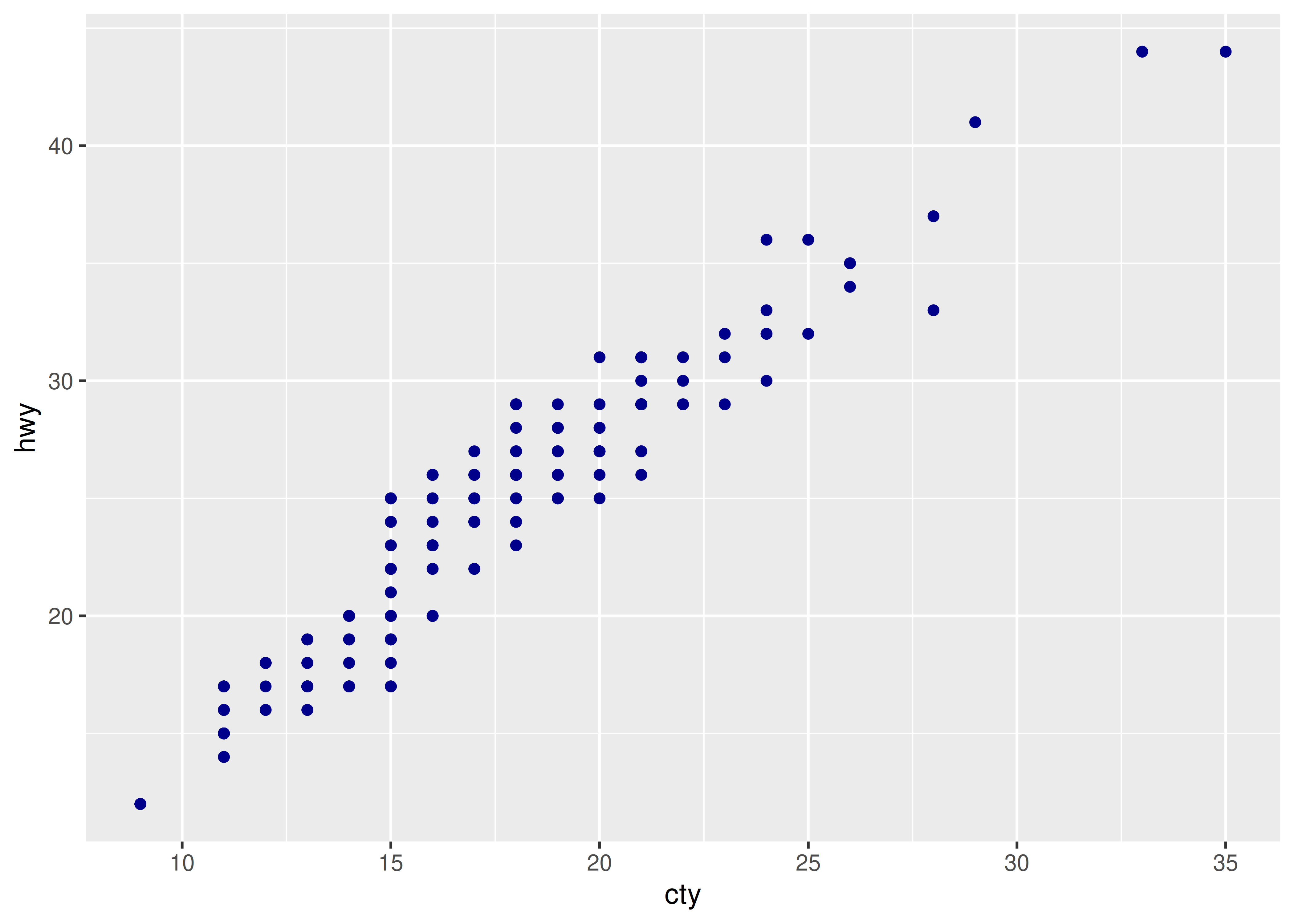

Esto es más útil si siempre tienes una columna que ya contiene colores. Aprenderá más sobre eso en Sección 12.6.

A veces resulta útil asignar la estética a constantes. Por ejemplo, si desea mostrar varias capas con diferentes parámetros, puede “name” cada capa:

ggplot(mpg, aes(displ, hwy)) + 
  geom_point() +
  geom_smooth(aes(colour = "loess"), method = "loess", se = FALSE) + 
  geom_smooth(aes(colour = "lm"), method = "lm", se = FALSE) +
  labs(colour = "Method")
#> `geom_smooth()` using formula = 'y ~ x'
#> `geom_smooth()` using formula = 'y ~ x'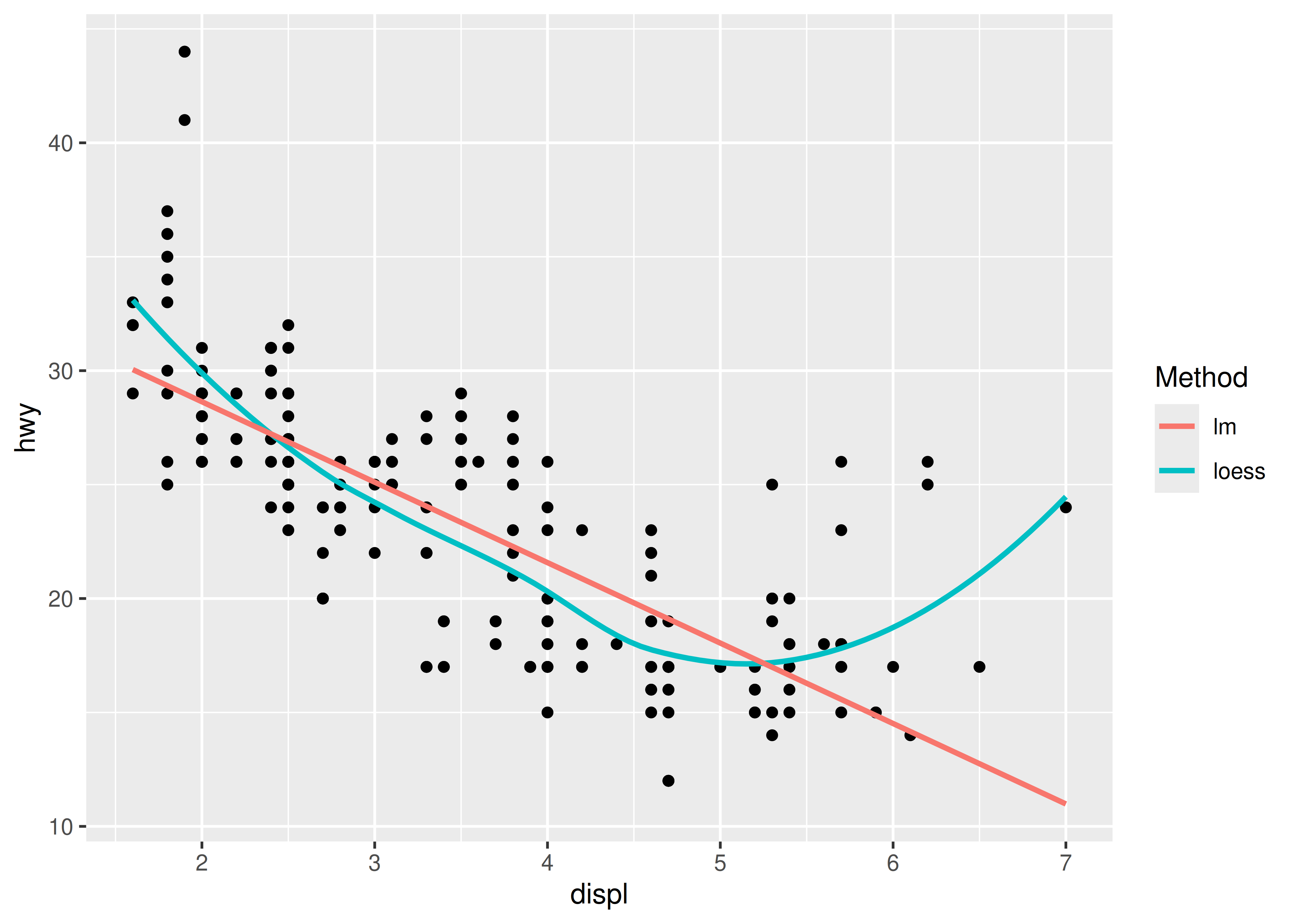

13.4.3 Ejercicios

Simplifique las siguientes especificaciones de la gráfica:

ggplot(mpg) + 
  geom_point(aes(mpg$displ, mpg$hwy))

ggplot() + 
 geom_point(mapping = aes(y = hwy, x = cty), data = mpg) +
 geom_smooth(data = mpg, mapping = aes(cty, hwy))

ggplot(diamonds, aes(carat, price)) + 
  geom_point(aes(log(brainwt), log(bodywt)), data = msleep)

¿Qué hace el siguiente código? ¿Funciona? ¿Tiene sentido? ¿Por qué por qué no?

ggplot(mpg) +
  geom_point(aes(class, cty)) + 
  geom_boxplot(aes(trans, hwy))

¿Qué sucede si intenta utilizar una variable continua en el eje x en una capa y una variable categórica en otra capa? ¿Qué pasa si lo haces en el orden inverso?

13.5 Geomas

Los objetos geométricos, o geoms para abreviar, realizan la representación real de la capa, controlando el tipo de trazado que crea. Por ejemplo, usar una geom de puntos creará un diagrama de dispersión, mientras que usar una geom de líneas creará un diagrama de líneas.

Primitivas gráficas:
- geom_blank(): no mostrar nada. Más útil para ajustar los límites de los ejes utilizando datos.
- geom_point(): puntos.
- geom_path(): Conecta las observaciones en el orden en que aparecen en los datos.
- geom_ribbon(): cintas, un camino con espesor vertical..
- geom_segment(): un segmento de línea, especificado por la posición inicial y final.
- geom_rect(): rectángulos.
- geom_polygon(): polígonos rellenos.
- geom_text(): texto.
Una variable:
- Discreta:
  - geom_bar(): mostrar la distribución de la variable discreta.
- Continua:
  - geom_histogram(): bin y contar variable continua, visualización con barras.
  - geom_density(): estimación de densidad suavizada.
  - geom_dotplot(): apila puntos individuales en un diagrama de puntos.
  - geom_freqpoly(): agrupa y cuenta variable continua, visualización con líneas.
Dos variables:
- Ambas continuas:
  - geom_point(): gráfico de dispersión.
  - geom_quantile(): regresión cuantil suavizada.
  - geom_rug(): gráficas marginales de alfombras.
  - geom_smooth(): línea suavizada de mejor ajuste.
  - geom_text(): etiquetas de texto.
- Distribución:
  - geom_bin2d(): agrupa en rectángulos y cuenta.
  - geom_density2d(): estimación de densidad 2d suavizada.
  - geom_hex(): agrupa en hexágonos y cuenta.
- Al menos una discreta:
  - geom_count(): contar el número de puntos en distintas ubicaciones
  - geom_jitter(): agitar aleatoriamente puntos superpuestos.
- Uno continuo, uno discreto:
  - geom_bar(stat = "identity"): un gráfico de barras de resúmenes precalculados.
  - geom_boxplot(): diagramas de caja.
  - geom_violin(): mostrar la densidad de valores en cada grupo.
- Una vez, uno continuo:
  - geom_area(): gráfica de área.
  - geom_line(): diagrama de líneas.
  - geom_step(): gráfica escalonada.
- Mostrar incertidumbre:
  - geom_crossbar(): barra vertical con centro.
  - geom_errorbar(): barras de error.
  - geom_linerange(): linea vertical.
  - geom_pointrange(): línea vertical con centro.
- Espacial:
  - geom_map(): versión rápida de geom_polygon() para datos de mapas.
Tres variables:
- geom_contour(): contornos.
- geom_tile(): mosaico el avión con rectángulos.
- geom_raster(): versión rápida de geom_tile() para mosaicos del mismo tamaño.

Cada geom tiene un conjunto de estéticas que comprende, algunas de las cuales deben proporcionarse. Por ejemplo, las geoms puntuales requieren la posición x e y, y comprenden la estética del color, el tamaño y la forma. Una barra requiere altura (ymax) y comprende el ancho, el color del borde y el color de relleno. Cada geom enumera su estética en la documentación.

Algunas geoms se diferencian principalmente en la forma en que están parametrizadas. Por ejemplo, puedes dibujar un cuadrado de tres maneras:

Al darle a geom_tile() la ubicación (x e y) y las dimensiones (width y height).
Dando a geom_rect() las posiciones superior (ymax), inferior (ymin), izquierda (xmin) y derecha (xmax).
Dándole a geom_polygon() un marco de datos de cuatro filas con las posiciones x e y de cada esquina.

Otras geomas relacionadas son:

geom_segment() y geom_line()
geom_area() y geom_ribbon().

Si hay parametrizaciones alternativas disponibles, elegir la adecuada para sus datos normalmente hará que sea mucho más fácil dibujar el gráfico que desea.

13.5.1 Ejercicios

Descargue e imprima la hoja de referencia de ggplot2 desde https://posit.co/resources/cheatsheets/ para tener una referencia visual útil para todas las geoms.
Mire la documentación para las geoms primitivas gráficas. ¿Qué estética utilizan? ¿Cómo puedes resumirlos en una forma compacta?
¿Cuál es la mejor manera de dominar una geom desconocida? Enumere tres recursos que le ayudarán a empezar.
Para cada uno de los gráficos siguientes, identifica la geom utilizada para dibujarlo.
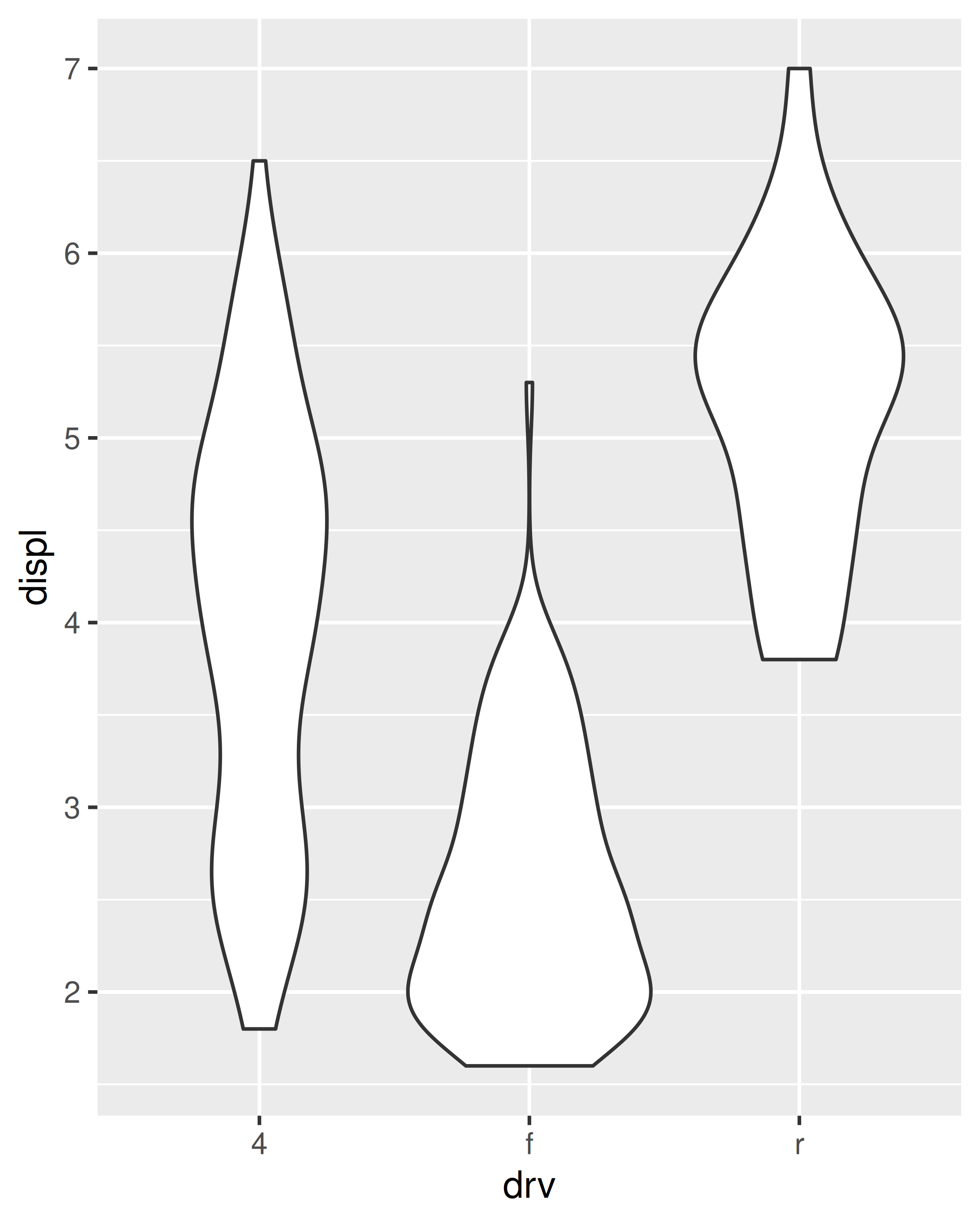
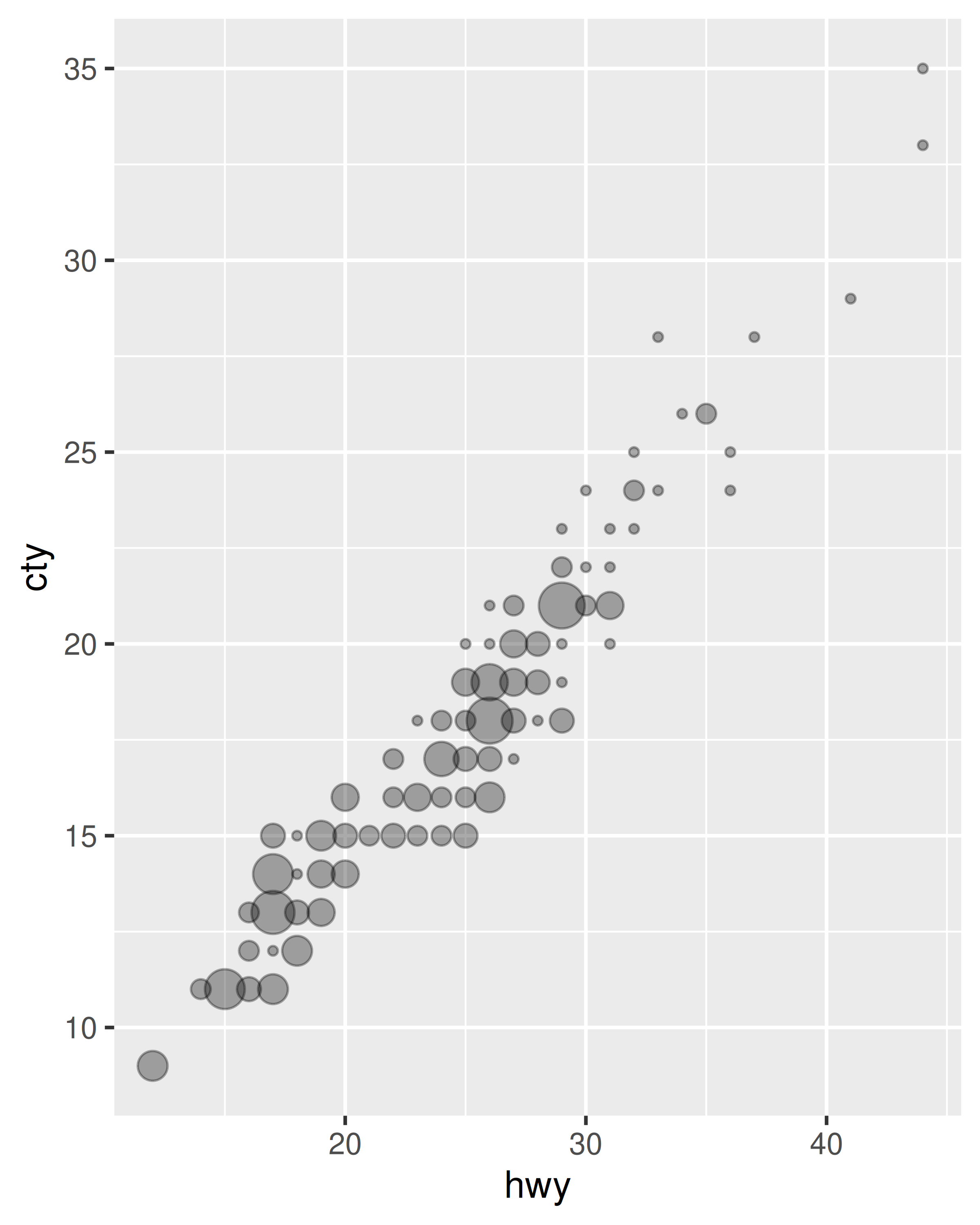
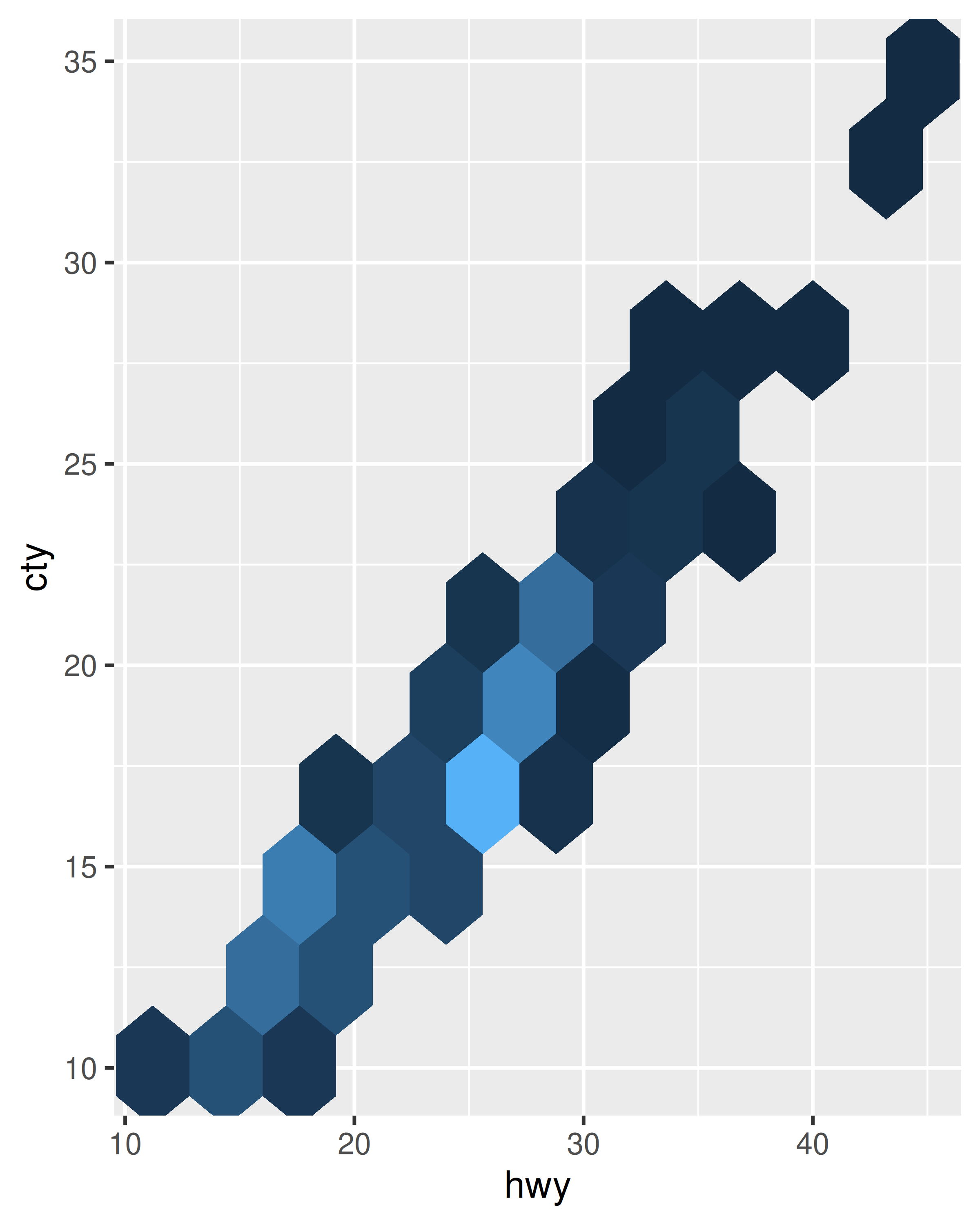
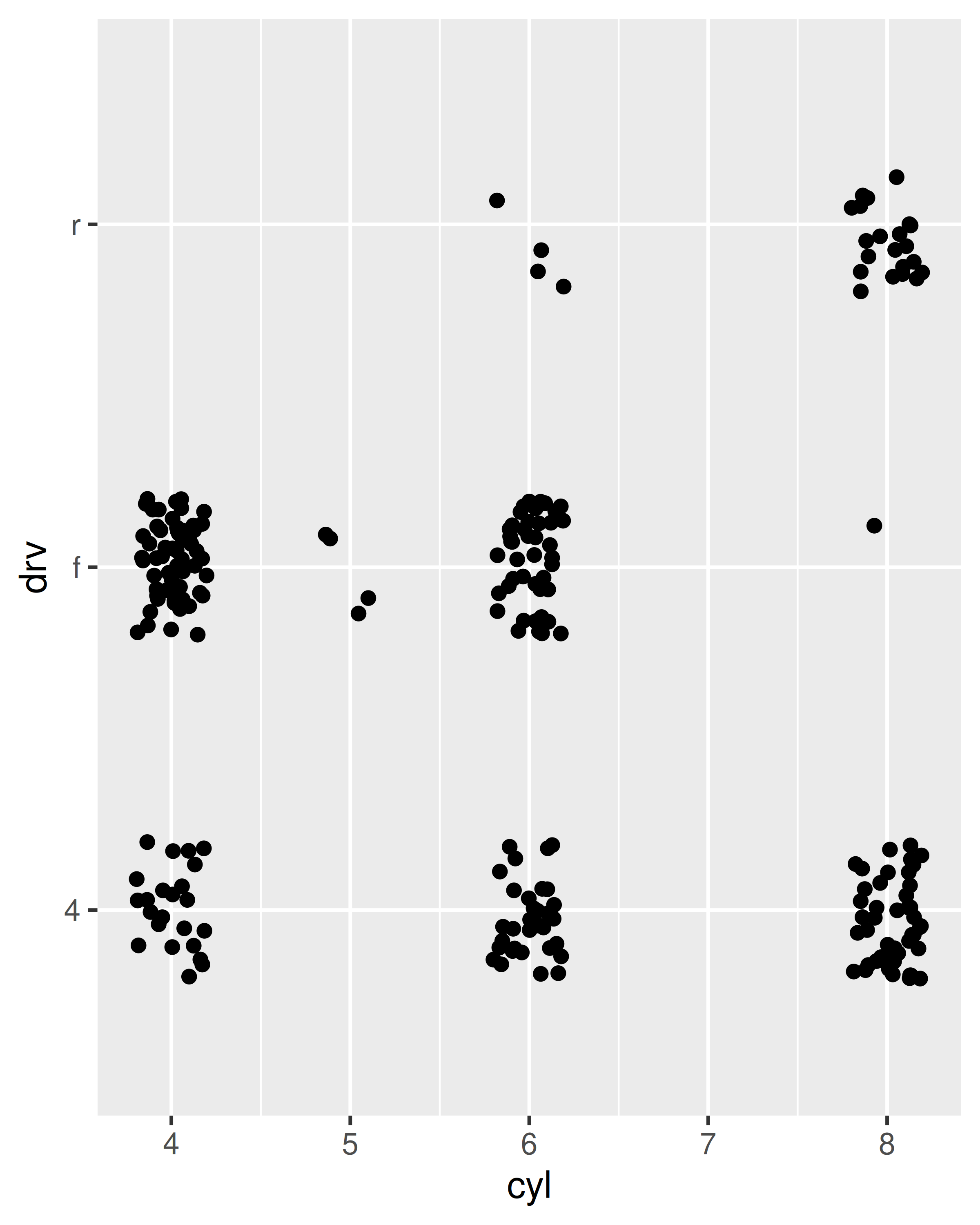
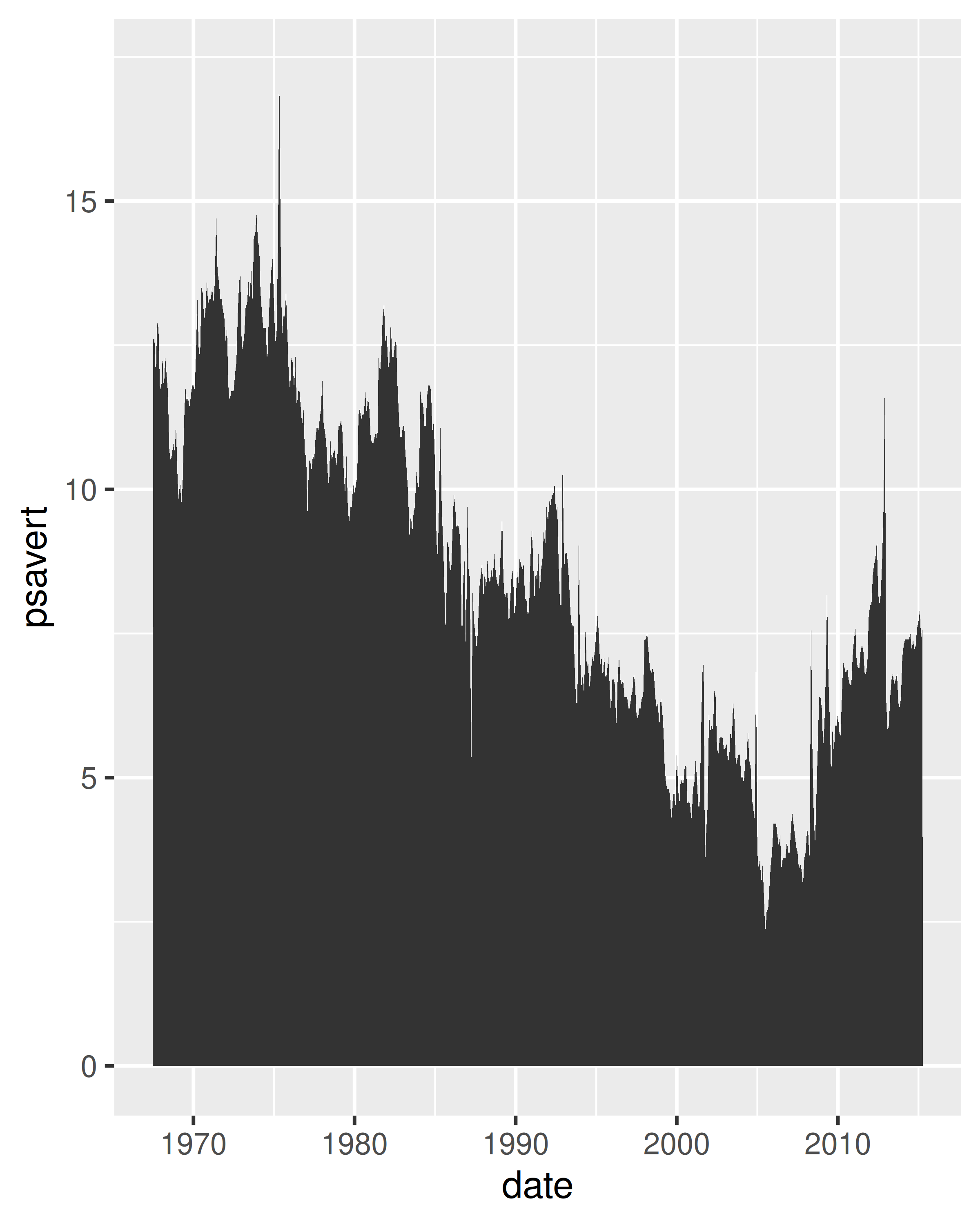
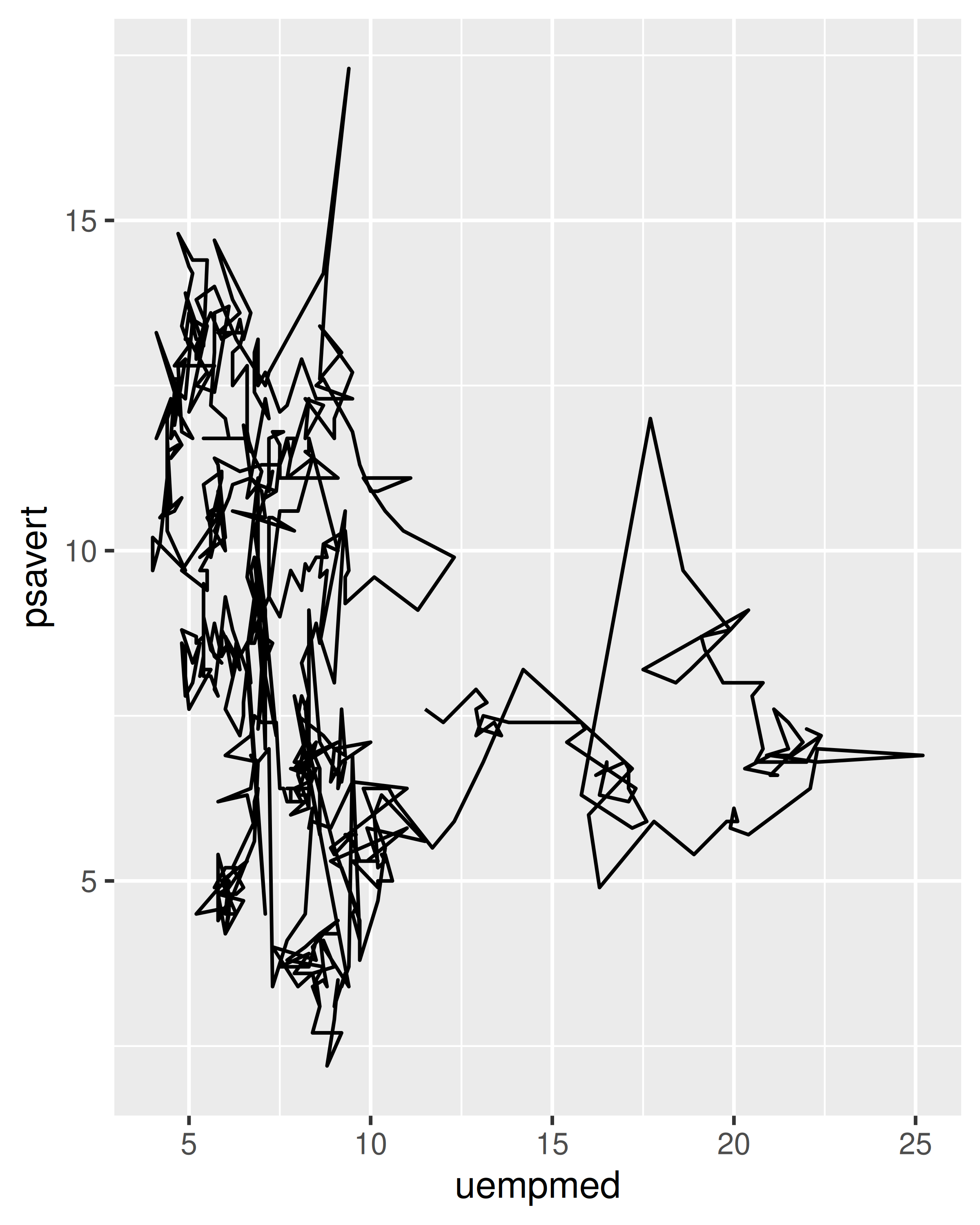
Para cada uno de los siguientes problemas, sugiera una geom útil:
- Muestra cómo una variable ha cambiado con el tiempo.
- Mostrar la distribución detallada de una sola variable.
- Centrar la atención en la tendencia general en un gran conjunto de datos.
- Dibujar un mapa.
- Etiquetar puntos periféricos.

13.6 Estadísticas

Una transformación estadística, o stat, transforma los datos, normalmente resumiéndolos de alguna manera. Por ejemplo, una estadística útil es la más suave, que calcula la media suavizada de y, condicionada a x. Ya has usado muchas de las estadísticas de ggplot2 porque se usan detrás de escena para generar muchas geoms importantes:

stat_bin(): geom_bar(), geom_freqpoly(), geom_histogram()
stat_bin2d(): geom_bin2d()
stat_bindot(): geom_dotplot()
stat_binhex(): geom_hex()
stat_boxplot(): geom_boxplot()
stat_contour(): geom_contour()
stat_quantile(): geom_quantile()
stat_smooth(): geom_smooth()
stat_sum(): geom_count()

Rara vez llamará a estas funciones directamente, pero es útil conocerlas porque su documentación a menudo proporciona más detalles sobre la transformación estadística correspondiente.

No se pueden crear otras estadísticas con una función geom_:

stat_ecdf(): calcular una gráfica de distribución acumulativa empírica.
stat_function(): calcular los valores de y a partir de una función de los valores de x.
stat_summary(): resumir los valores de y en distintos valores de x.
stat_summary2d(), stat_summary_hex(): resumir los valores agrupados.
stat_qq(): realizar cálculos para una gráfica cuantil-cuantil.
stat_spoke(): convertir ángulo y radio en posición.
stat_unique(): eliminar filas duplicadas.

Hay dos formas de utilizar estas funciones. Puede agregar una función stat_() y anular la estadística predeterminada, o agregar una función geom_() y anular la estadística predeterminada:

ggplot(mpg, aes(trans, cty)) + 
  geom_point() + 
  stat_summary(geom = "point", fun = "mean", colour = "red", size = 4)

ggplot(mpg, aes(trans, cty)) + 
  geom_point() + 
  geom_point(stat = "summary", fun = "mean", colour = "red", size = 4)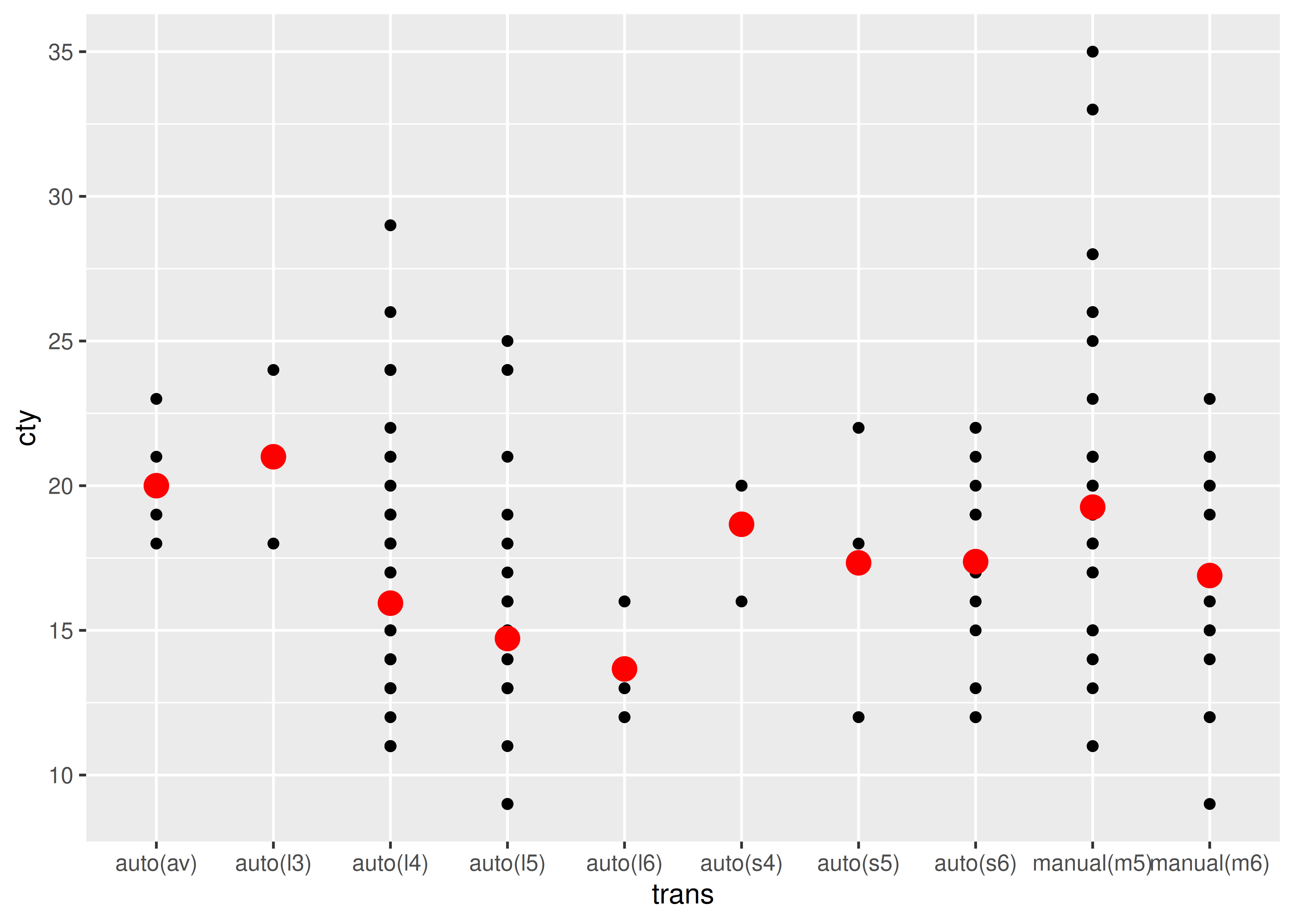

Creemos que es mejor utilizar el segundo formulario porque deja más claro que se muestra un resumen, no los datos sin procesar.

13.6.1 Variables generadas

Internamente, una estadística toma un marco de datos como entrada y devuelve un marco de datos como salida, por lo que una estadística puede agregar nuevas variables al conjunto de datos original. Es posible asignar la estética a estas nuevas variables. Por ejemplo, stat_bin, la estadística utilizada para crear histogramas, produce las siguientes variables:

count, el número de observaciones en cada contenedor
density, la densidad de observaciones en cada contenedor (porcentaje del total/ancho de barra)
x, el centro del contenedor

Estas variables generadas se pueden utilizar en lugar de las variables presentes en el conjunto de datos original. Por ejemplo, la geom de histograma predeterminada asigna la altura de las barras al número de observaciones (count), pero si prefieres un histograma más tradicional, puedes usar la densidad (density). Para hacer referencia a una variable generada como densidad, “after_stat()” debe ajustar el nombre. Esto evita confusiones en caso de que el conjunto de datos original incluya una variable con el mismo nombre que una variable generada y deja claro a cualquier lector posterior del código que esta variable fue generada por una estadística. Cada estadística enumera las variables que crea en su documentación. Compare los ejes y en estos dos gráficos:

ggplot(diamonds, aes(price)) + 
  geom_histogram(binwidth = 500)

ggplot(diamonds, aes(price)) + 
  geom_histogram(aes(y = after_stat(density)), binwidth = 500)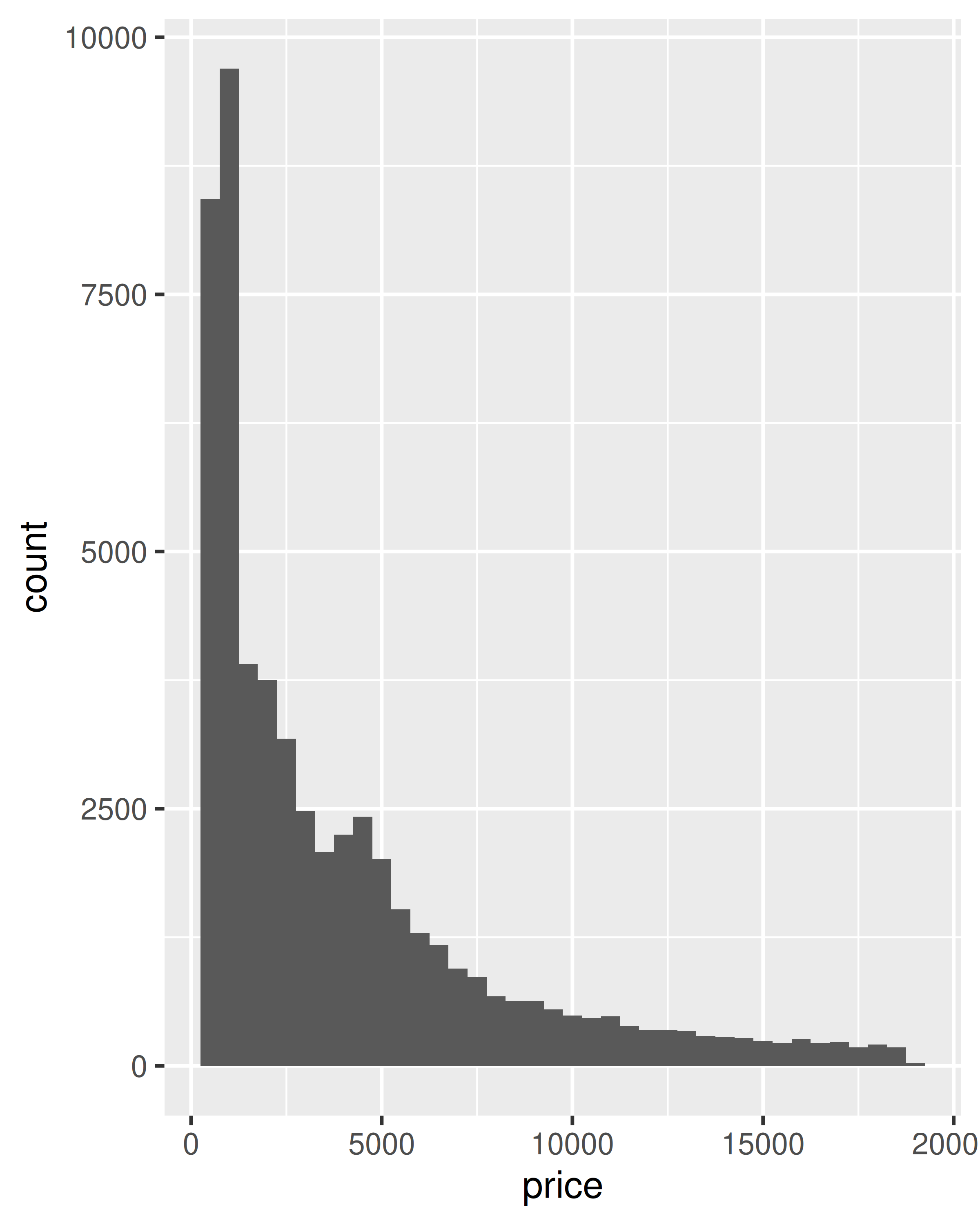

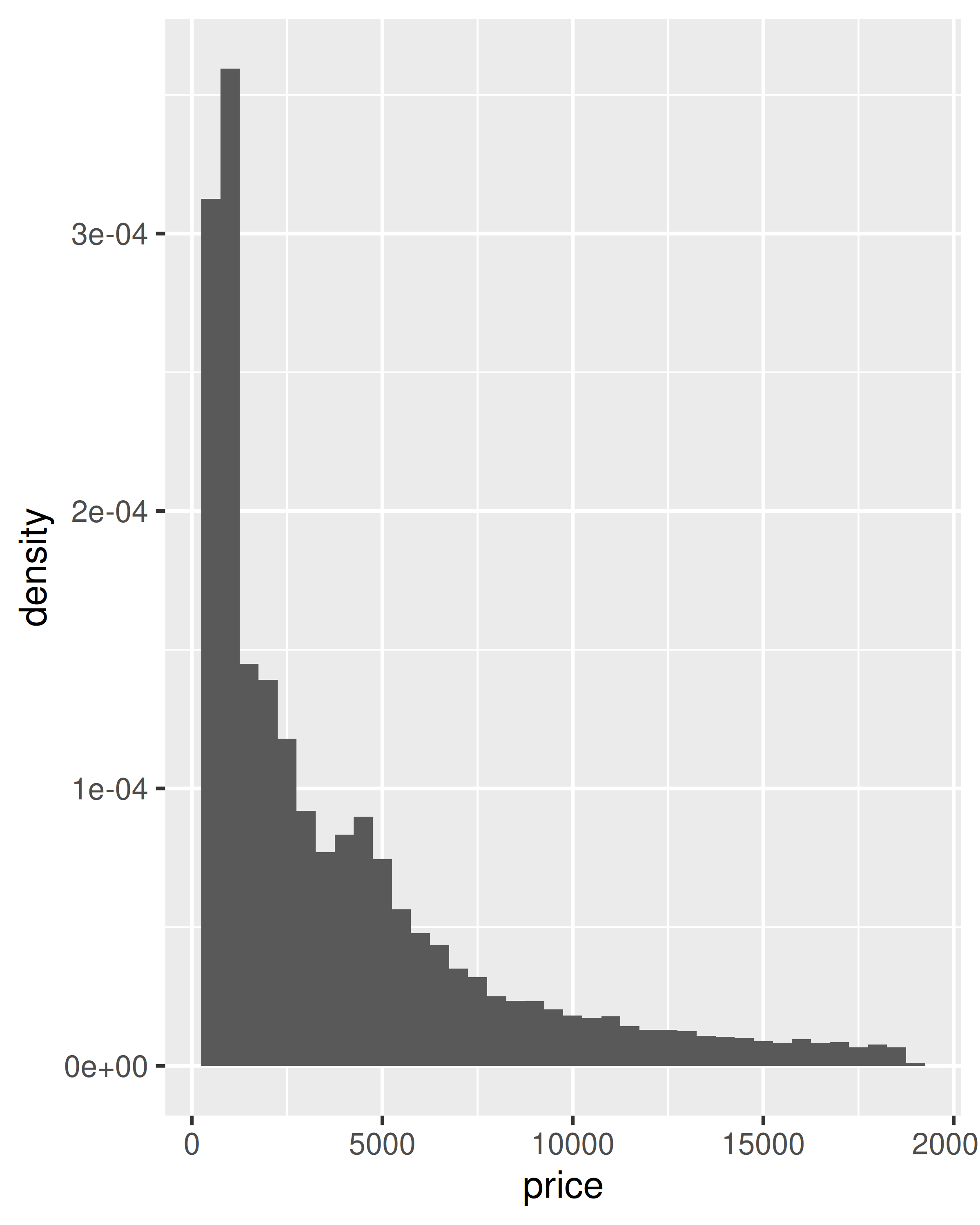
Esta técnica es particularmente útil cuando desea comparar la distribución de múltiples grupos que tienen tamaños muy diferentes. Por ejemplo, es difícil comparar la distribución del price dentro del cut porque algunos grupos son bastante pequeños. Es más fácil comparar si estandarizamos cada grupo para que ocupe la misma área:

ggplot(diamonds, aes(price, colour = cut)) + 
  geom_freqpoly(binwidth = 500) +
  theme(legend.position = "none")

ggplot(diamonds, aes(price, colour = cut)) + 
  geom_freqpoly(aes(y = after_stat(density)), binwidth = 500) + 
  theme(legend.position = "none")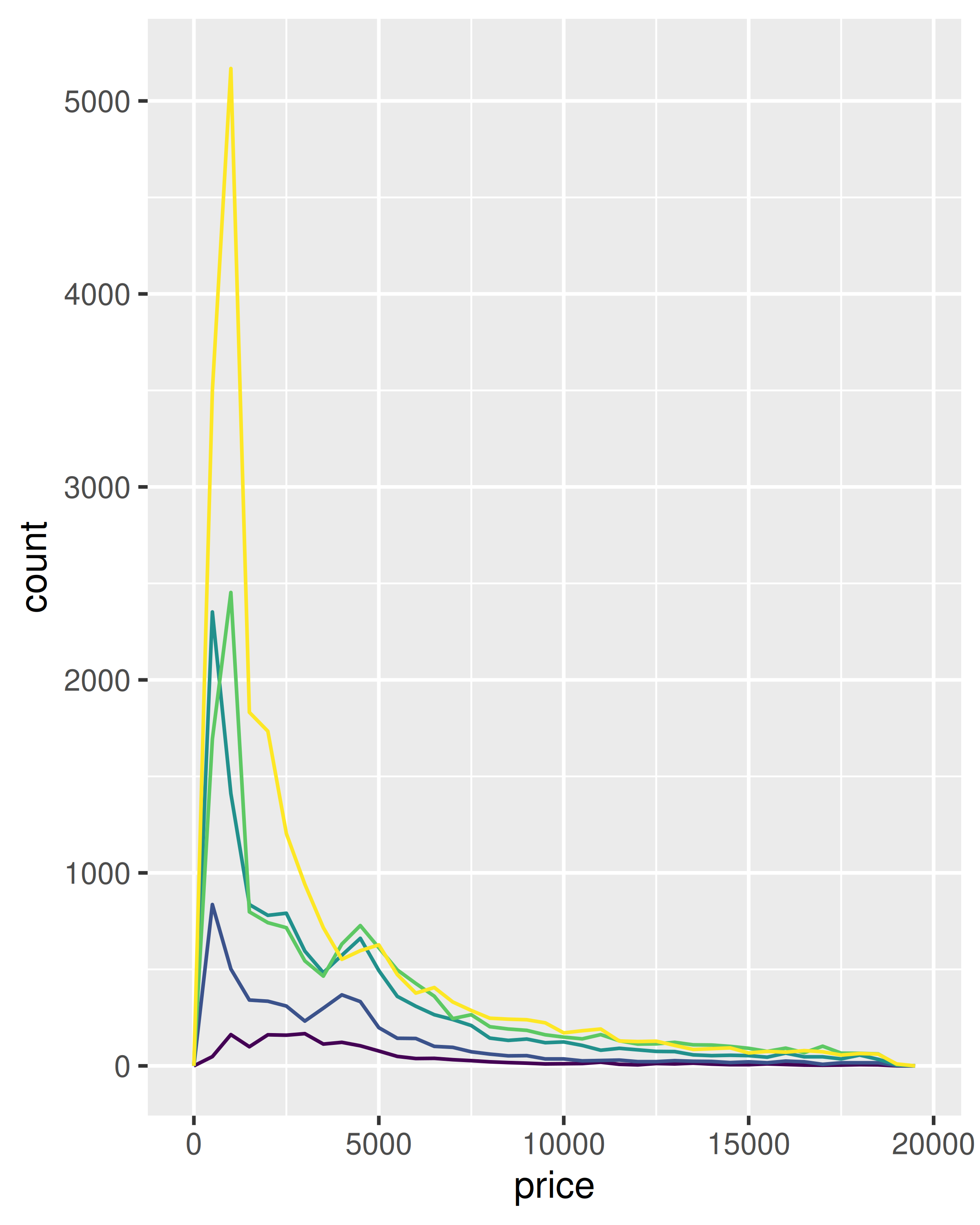

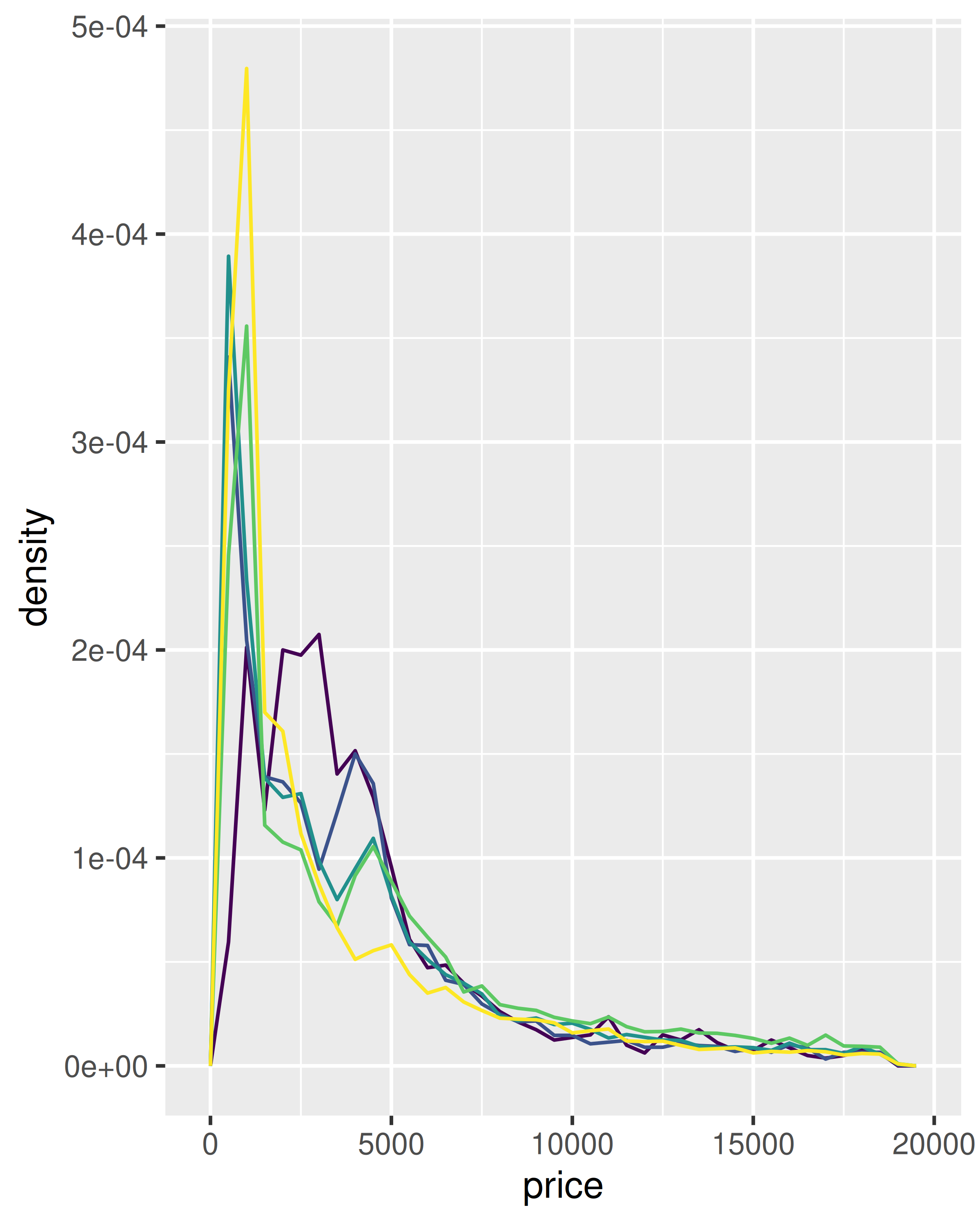
El resultado de este complot es bastante sorprendente: los diamantes de baja calidad parecen ser más caros en promedio.

13.6.2 Ejercicios

El siguiente código crea un conjunto de datos similar a stat_smooth(). Utilice las geoms apropiadas para imitar la visualización predeterminada geom_smooth().

mod <- loess(hwy ~ displ, data = mpg)
smoothed <- data.frame(displ = seq(1.6, 7, length = 50))
pred <- predict(mod, newdata = smoothed, se = TRUE) 
smoothed$hwy <- pred$fit
smoothed$hwy_lwr <- pred$fit - (1.96 * pred$se.fit)
smoothed$hwy_upr <- pred$fit + (1.96 * pred$se.fit)

¿Qué estadísticas se utilizaron para crear las siguientes gráficas?
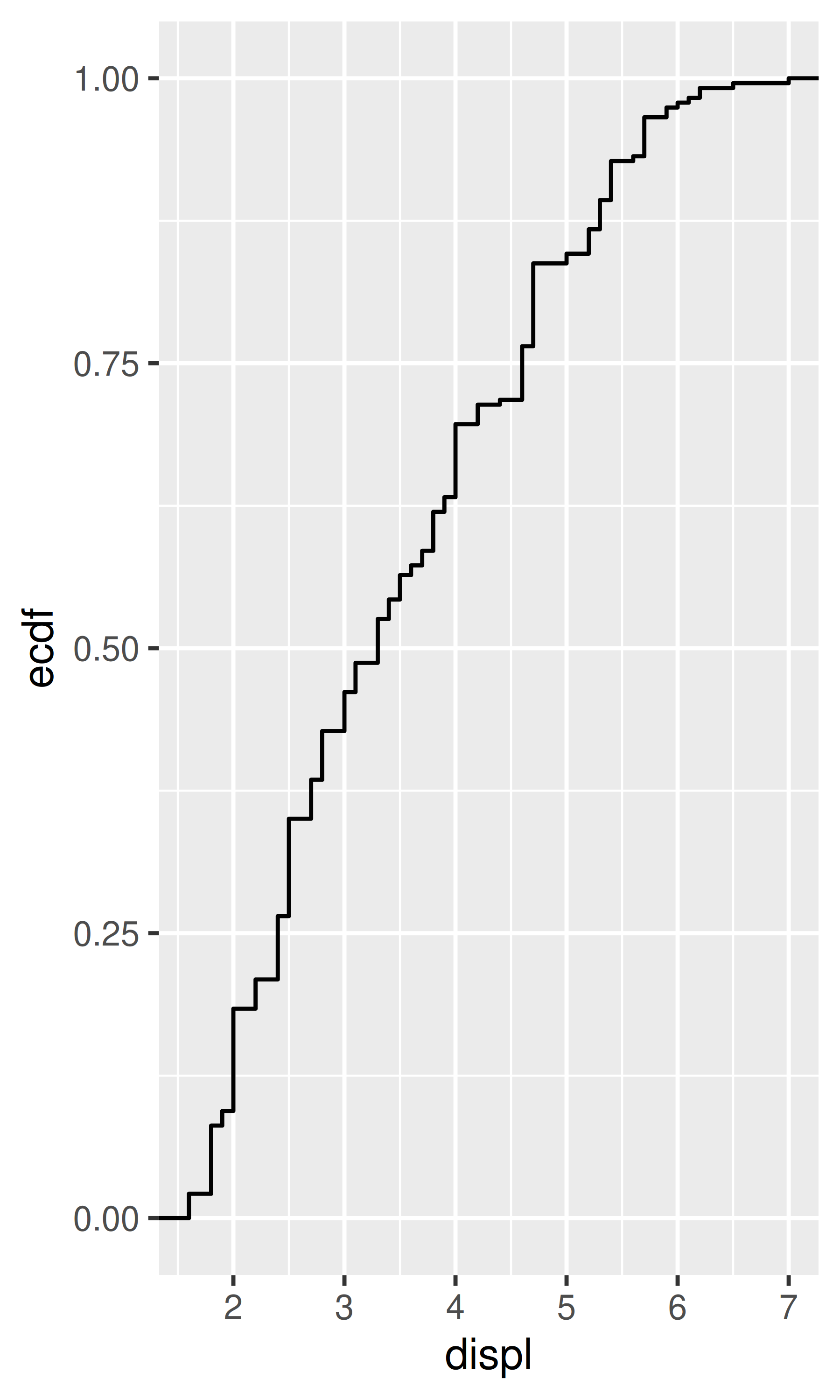
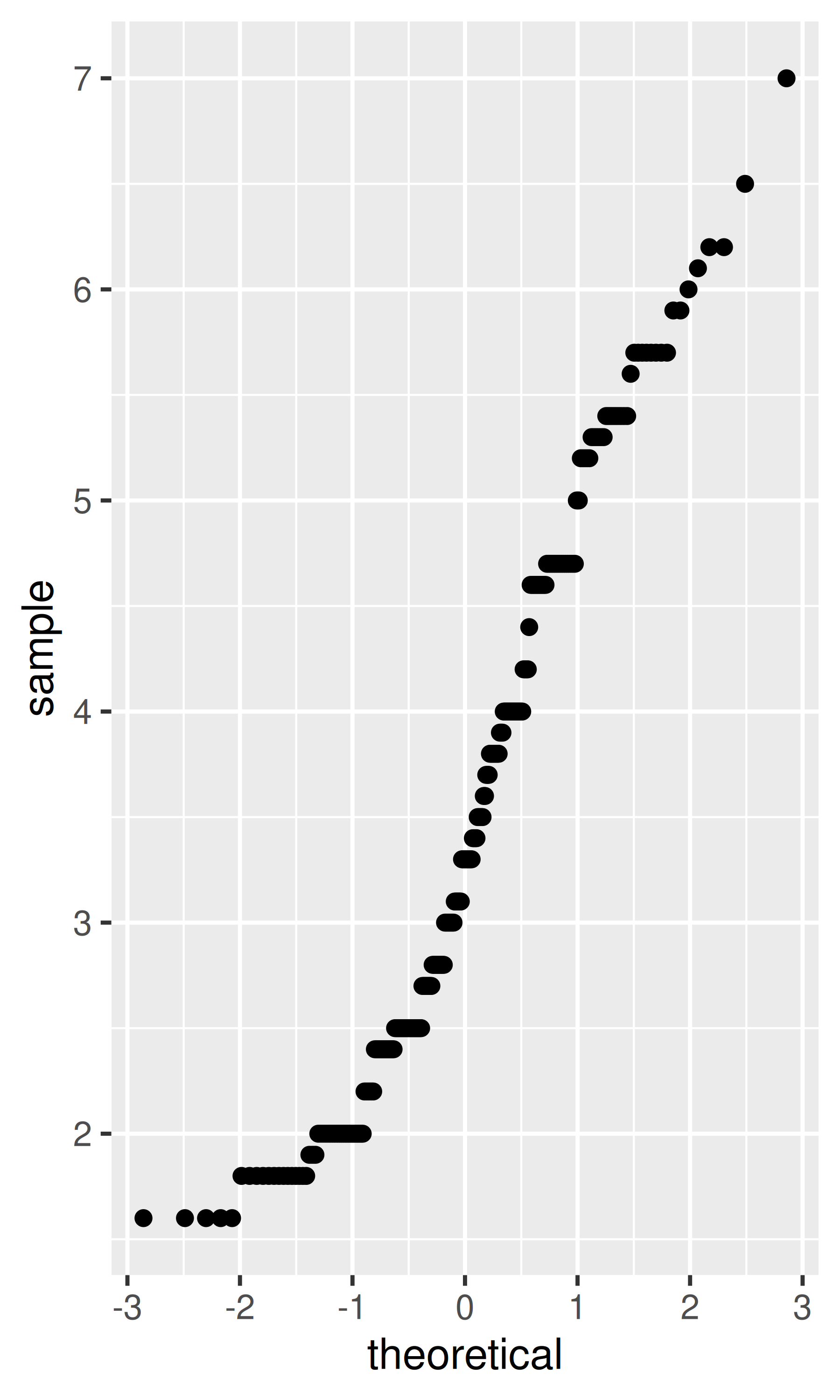
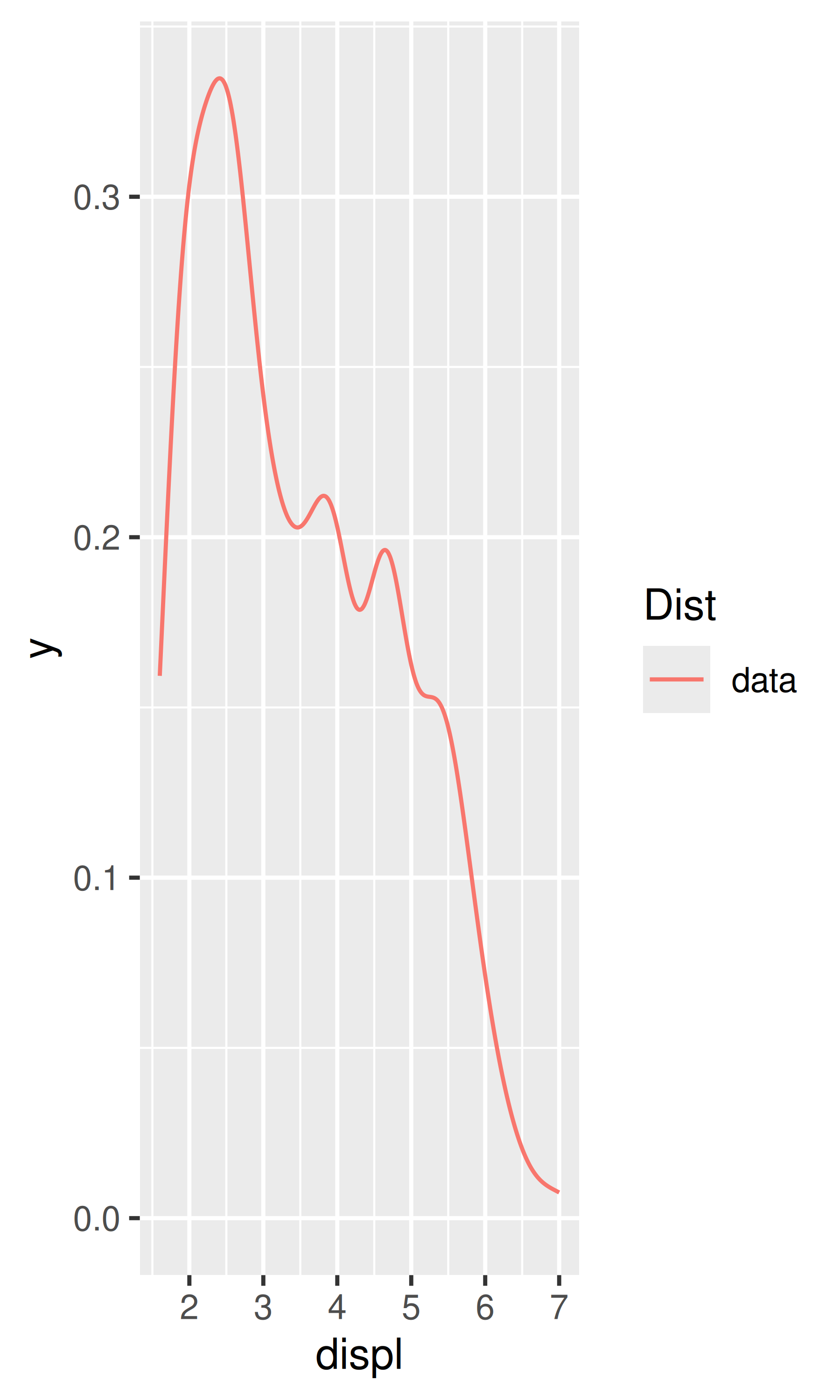
Lea la ayuda para stat_sum() y luego use geom_count() para crear un gráfico que muestre la proporción de automóviles que tienen cada combinación de drv y trans.

13.7 Ajustes de posición

Los ajustes de posición aplican ajustes menores a la posición de los elementos dentro de una capa. Tres ajustes se aplican principalmente a las barras:

position_stack(): apile barras (o áreas) superpuestas una encima de la otra.
position_fill(): apile barras superpuestas, escalando para que la parte superior esté siempre en 1.
position_dodge(): coloque barras superpuestas (o diagramas de caja) una al lado de la otra.

dplot <- ggplot(diamonds, aes(color, fill = cut)) + 
  xlab(NULL) + ylab(NULL) + theme(legend.position = "none")
# La pila de posiciones es la predeterminada para las barras, por lo que `geom_bar()` 
# es equivalente a `geom_bar(position = "stack")`.
dplot + geom_bar()
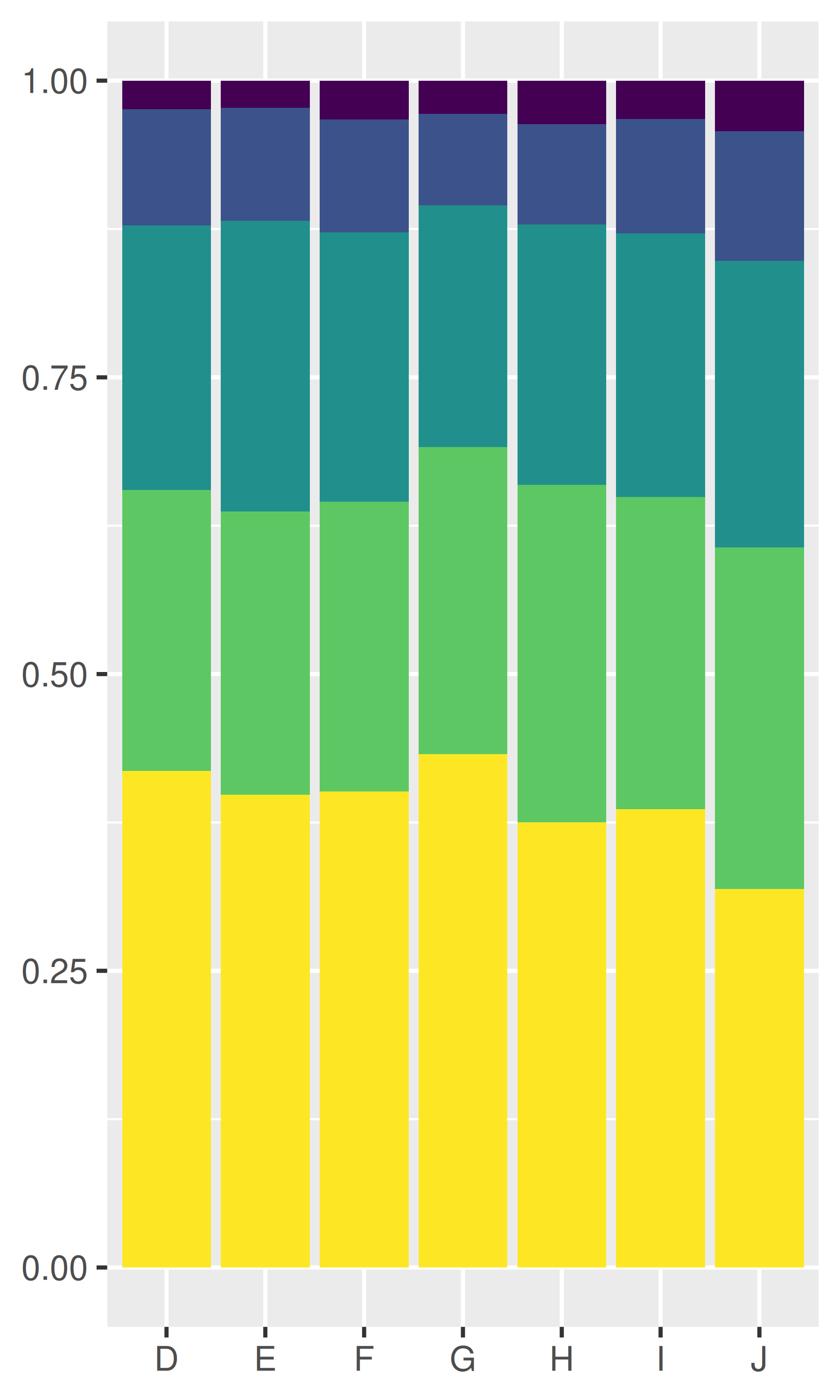
dplot + geom_bar(position = "fill")
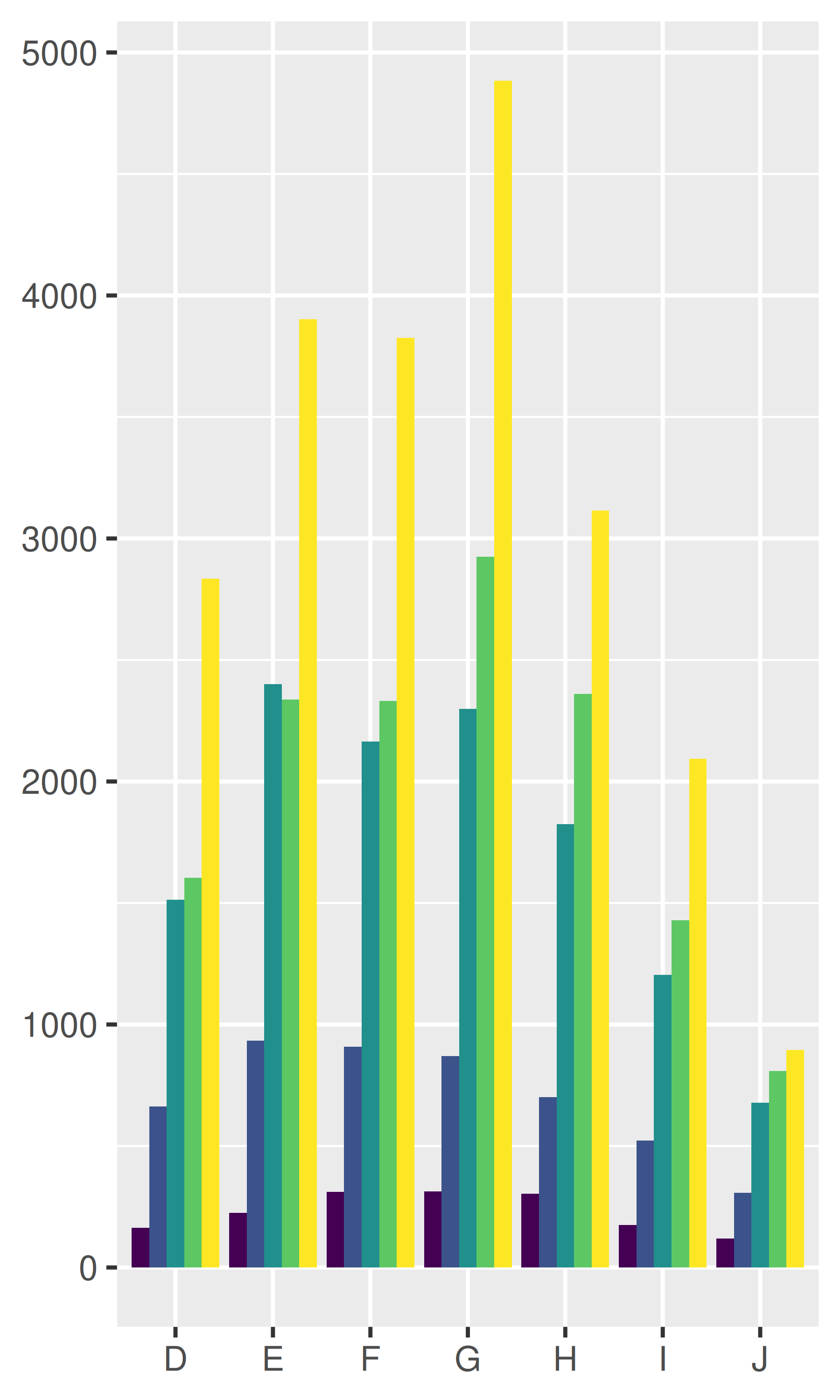
dplot + geom_bar(position = "dodge")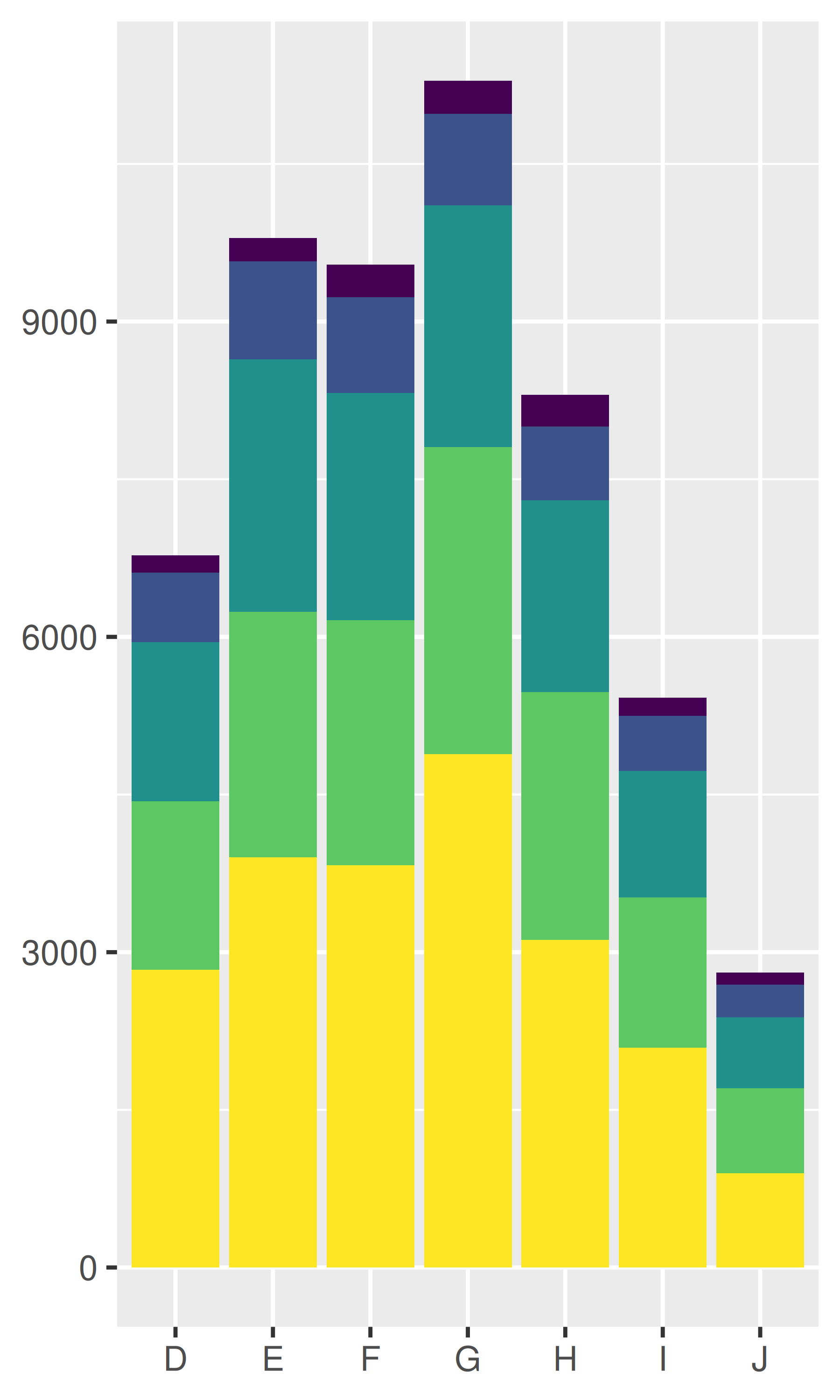

También hay un ajuste de posición que no hace nada: position_identity(). El ajuste de la posición de identidad no es útil para las barras, porque cada barra oscurece las barras detrás, pero hay muchas geoms que no necesitan ajuste, como las líneas:

dplot + geom_bar(position = "identity", alpha = 1 / 2, colour = "grey50")

ggplot(diamonds, aes(color, colour = cut)) + 
  geom_line(aes(group = cut), stat = "count") + 
  xlab(NULL) + ylab(NULL) + 
  theme(legend.position = "none")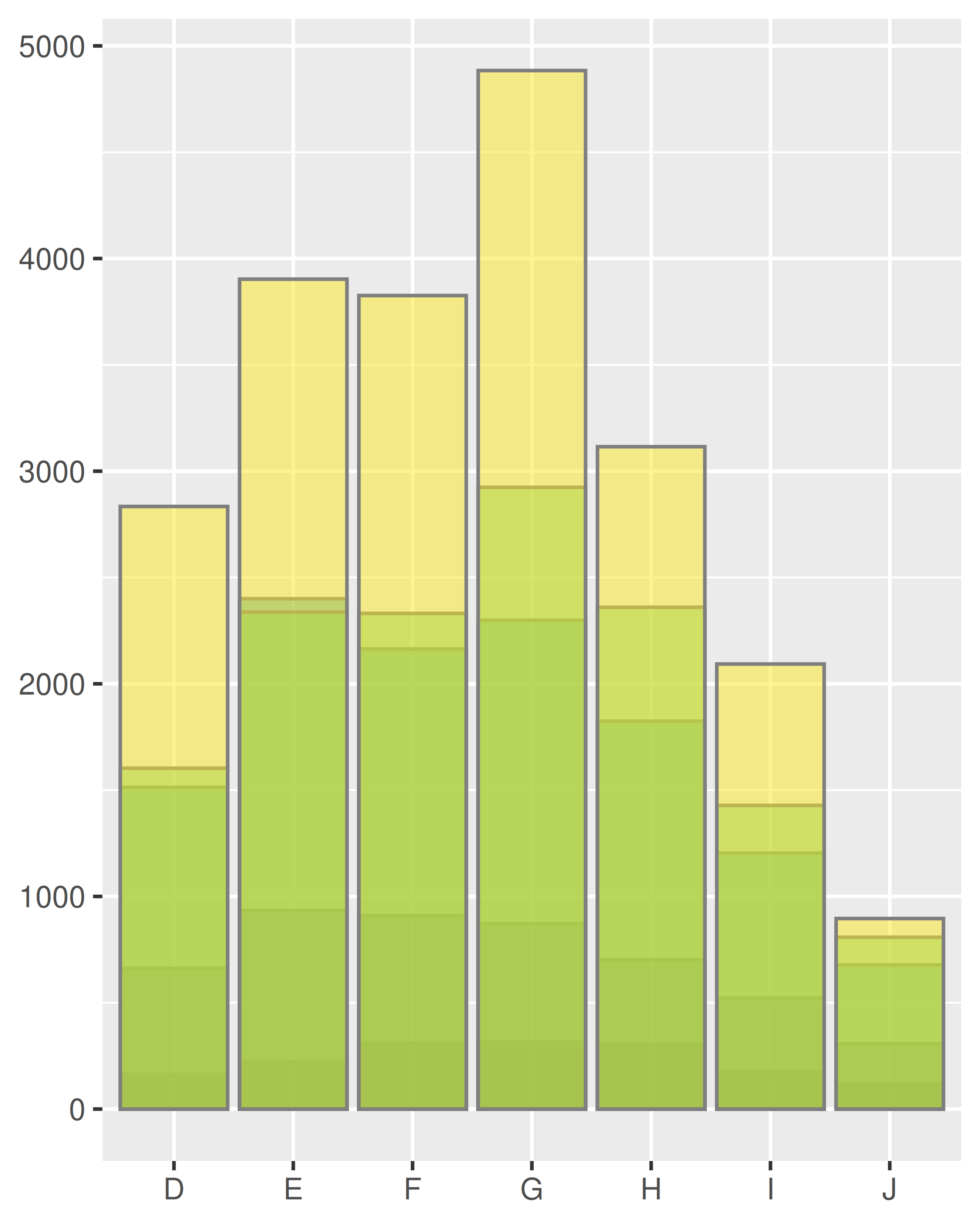

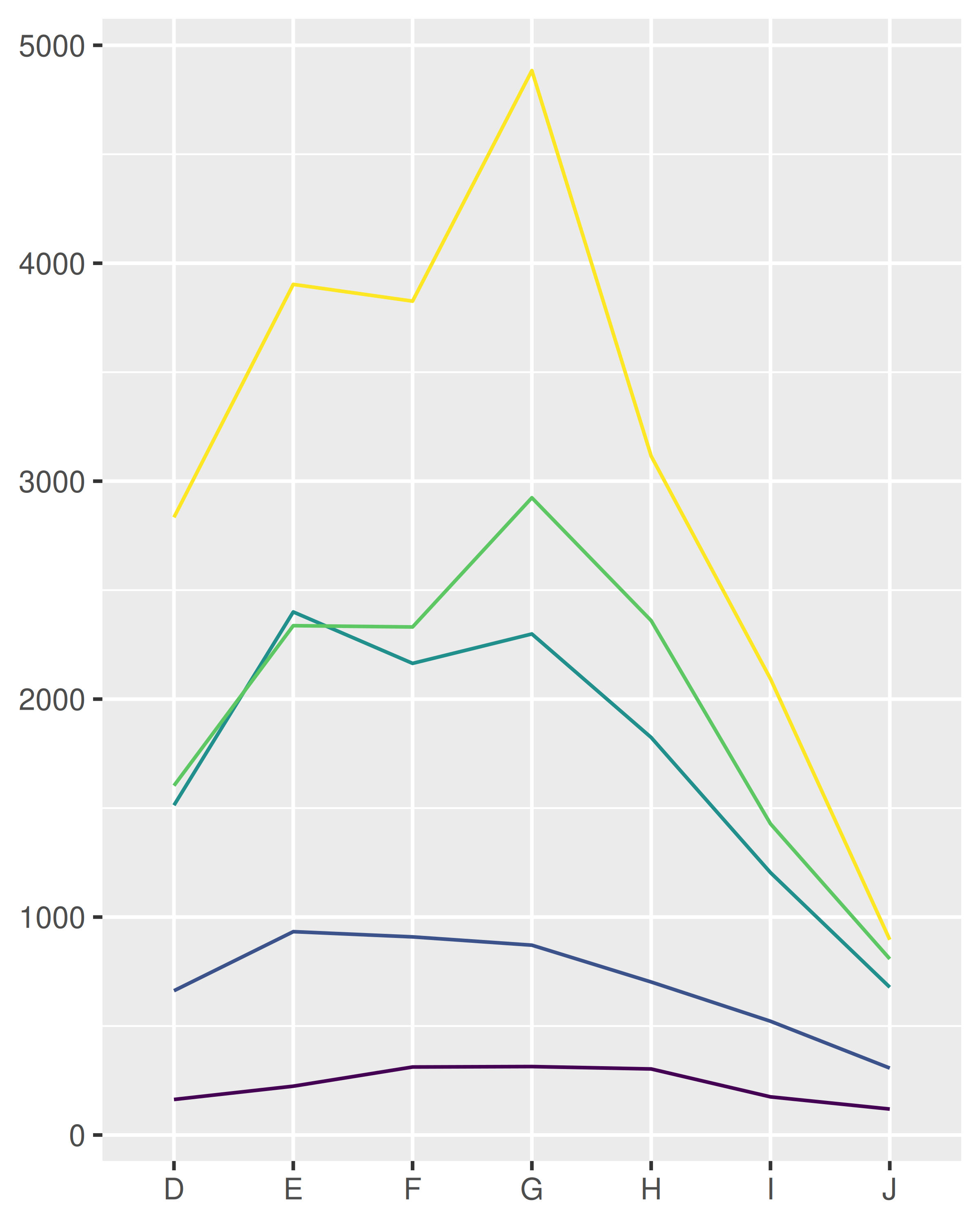
Hay tres ajustes de posición que son principalmente útiles para los puntos:

position_nudge(): mover puntos con un desplazamiento fijo.
position_jitter(): agregue un poco de ruido aleatorio a cada posición.
position_jitterdodge(): Esquiva puntos dentro de los grupos y luego agrega un poco de ruido aleatorio.

Tenga en cuenta que la forma en que pasa parámetros para posicionar ajustes difiere según las estadísticas y las geoms. En lugar de incluir argumentos adicionales en ..., construyes un objeto de ajuste de posición y proporcionas argumentos adicionales en la llamada:

ggplot(mpg, aes(displ, hwy)) + 
  geom_point(position = "jitter")

ggplot(mpg, aes(displ, hwy)) + 
  geom_point(position = position_jitter(width = 0.05, height = 0.5))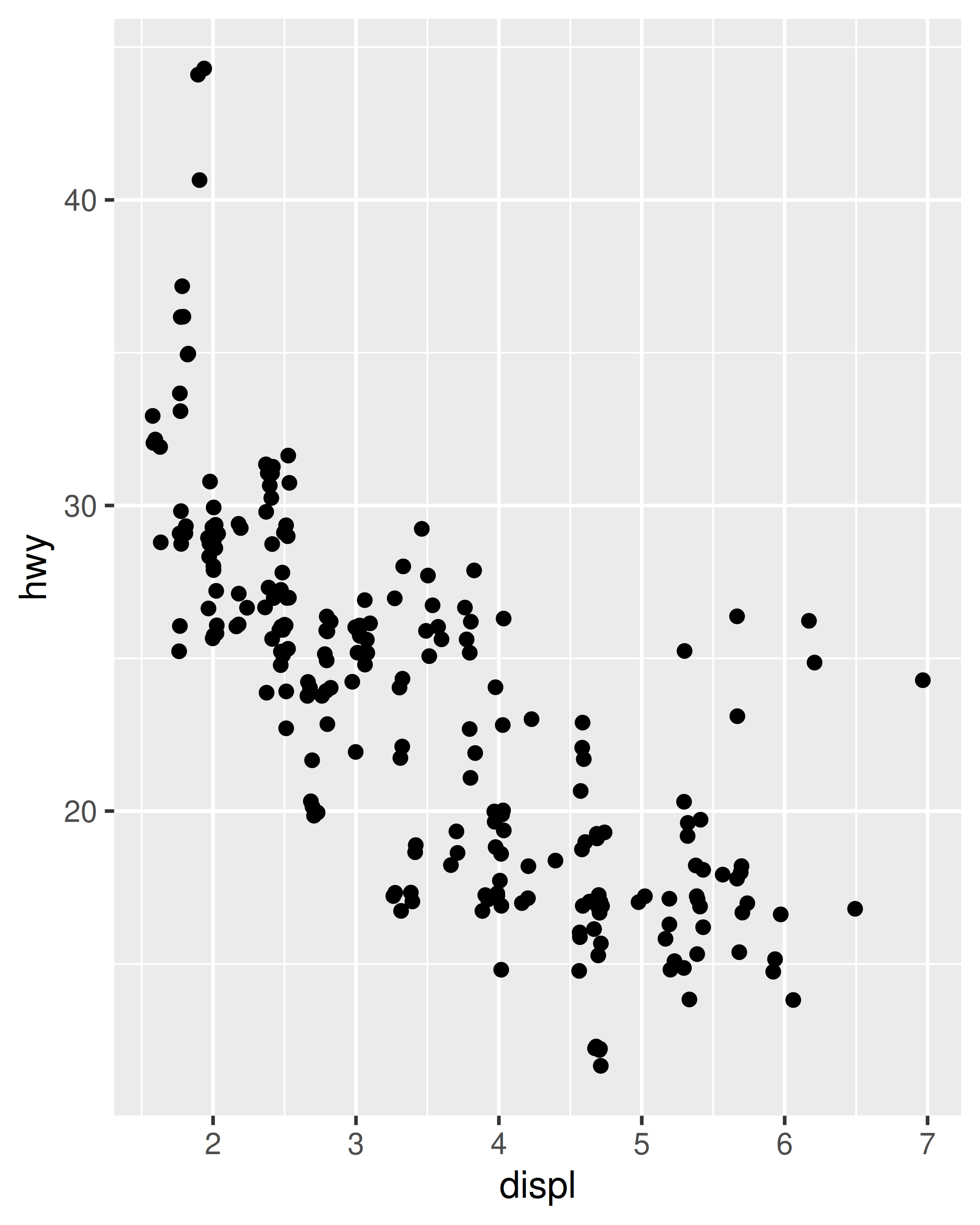

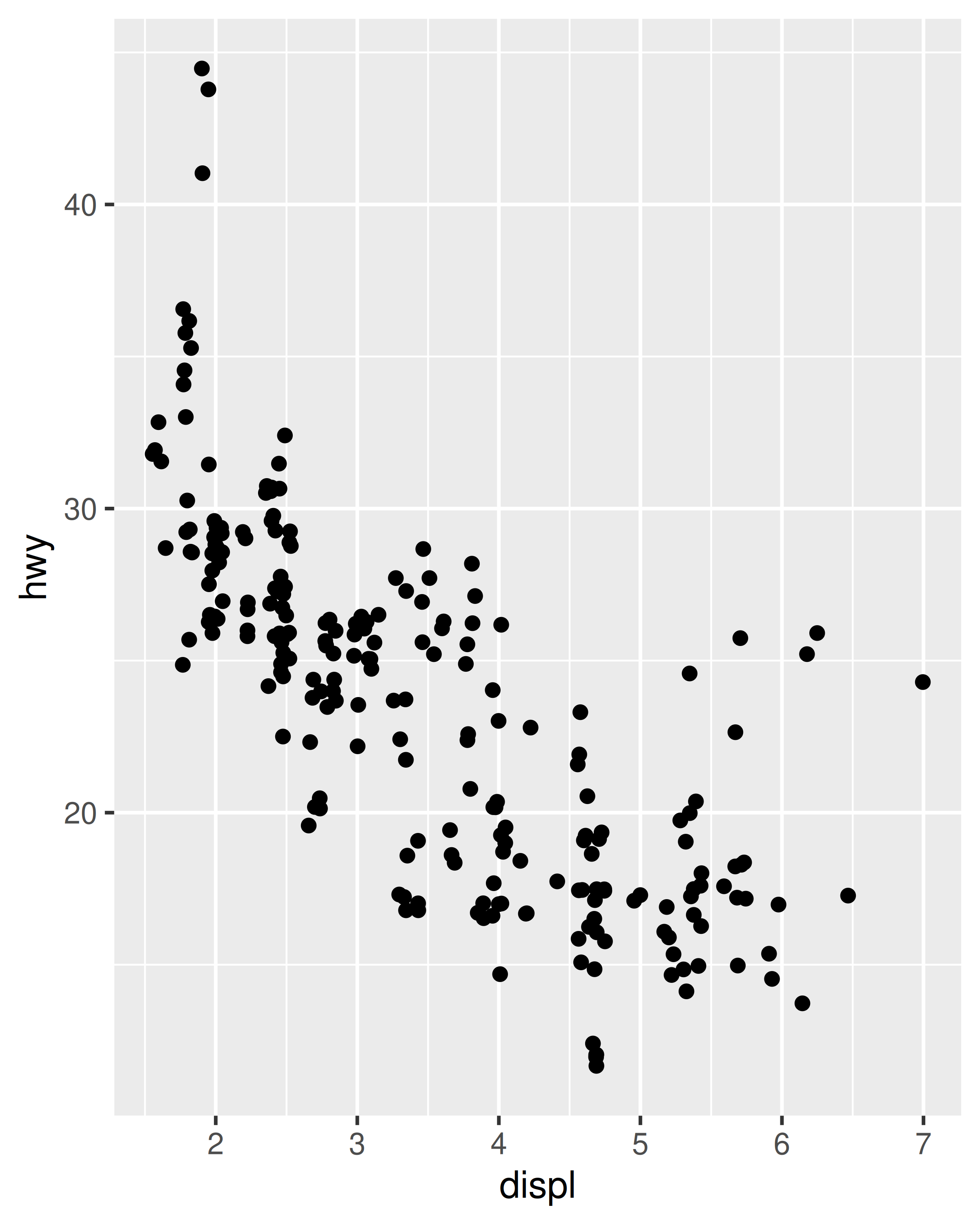
Esto es bastante detallado, por lo que geom_jitter() proporciona un atajo conveniente:

ggplot(mpg, aes(displ, hwy)) + 
  geom_jitter(width = 0.05, height = 0.5)

Los datos continuos normalmente no se superponen exactamente y, cuando lo hacen (debido a la alta densidad de datos), los ajustes menores, como la fluctuación, a menudo son insuficientes para solucionar el problema. Por este motivo, los ajustes de posición suelen ser más útiles para datos discretos.

13.7.1 Ejercicios

¿Cuándo podrías usar position_nudge()? Lea la documentación.
Muchos ajustes de posición sólo se pueden utilizar con unas pocas geoms. Por ejemplo, no puedes apilar diagramas de caja o barras de errores. ¿Por qué no? ¿Qué propiedades debe poseer una geom para ser apilable? ¿Qué propiedades debe poseer para ser esquivable?
¿Por qué deberías usar geom_jitter() en lugar de geom_count()? ¿Cuáles son las ventajas y desventajas de cada técnica?
¿Cuándo podrías utilizar un diagrama de áreas apiladas? ¿Cuáles son las ventajas y desventajas en comparación con un diagrama de líneas?