diamonds
#> # A tibble: 53,940 × 10
#> carat cut color clarity depth table price x y z
#> <dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl>
#> 1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
#> 2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
#> 3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
#> 4 0.29 Premium I VS2 62.4 58 334 4.2 4.23 2.63
#> 5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
#> 6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
#> # ℹ 53,934 more rows5 Resúmenes estadísticos
You are reading the work-in-progress third edition of the ggplot2 book. This chapter is currently a dumping ground for ideas, and we don’t recommend reading it.
5.1 Revelando incertidumbre
Si tiene información sobre la incertidumbre presente en sus datos, ya sea de un modelo o de supuestos distributivos, es una buena idea mostrarla. Hay cuatro familias básicas de geoms que se pueden usar para este trabajo, dependiendo de si los valores de x son discretos o continuos, y si desea o no mostrar la mitad del intervalo, o solo la extensión:
- Discreto x, rango:
geom_errorbar(),geom_linerange() - Discreto x, rango & centro:
geom_crossbar(),geom_pointrange() - Continuo x, rango:
geom_ribbon() - Continuo x, rango & centro:
geom_smooth(stat = "identity")
Estas geoms suponen que está interesado en la distribución de y condicional a x y utilizan la estética ymin e ymax para determinar el rango de los valores de y. Si quieres lo contrario, mira Sección 15.1.2.
y <- c(18, 11, 16)
df <- data.frame(x = 1:3, y = y, se = c(1.2, 0.5, 1.0))
base <- ggplot(df, aes(x, y, ymin = y - se, ymax = y + se))
base + geom_crossbar()
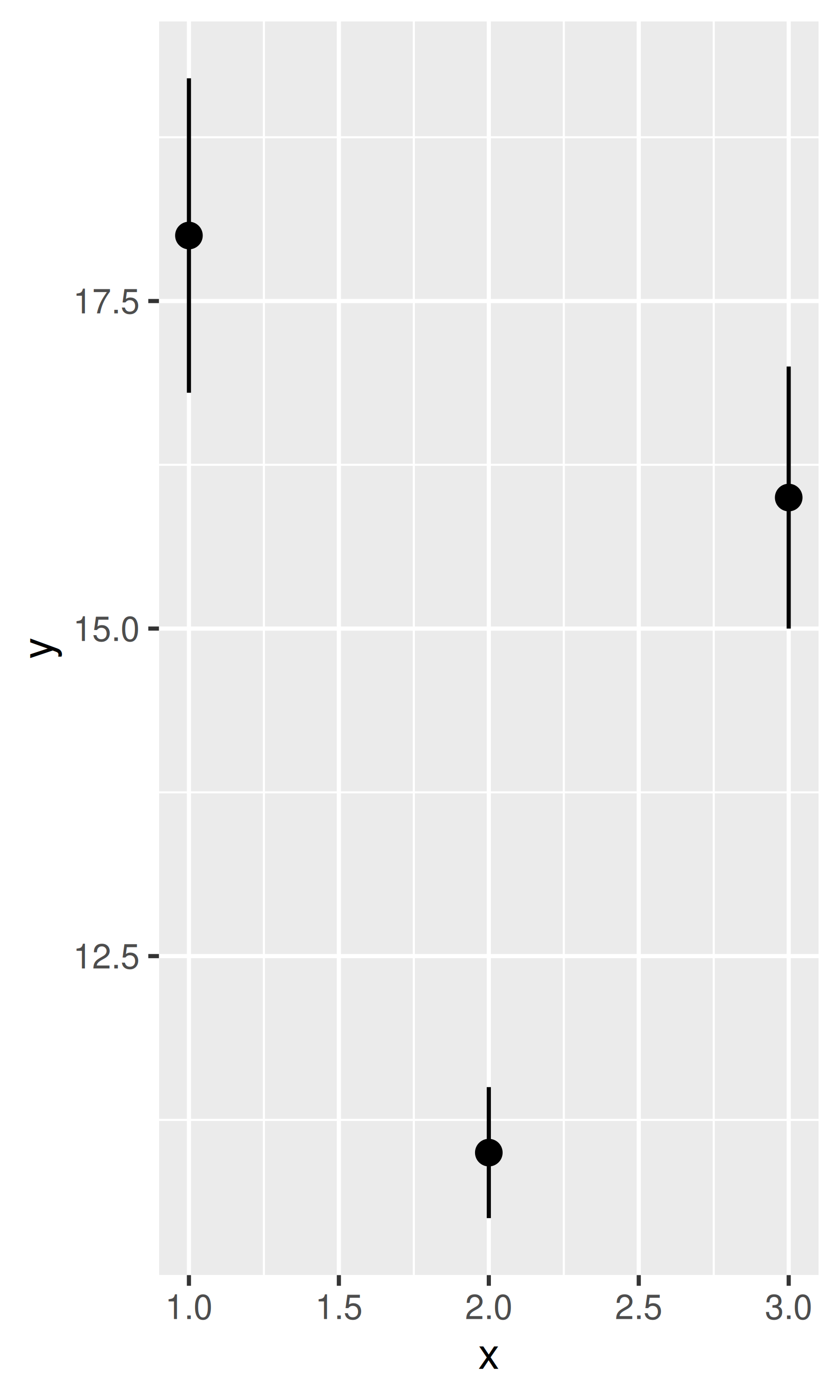
base + geom_pointrange()
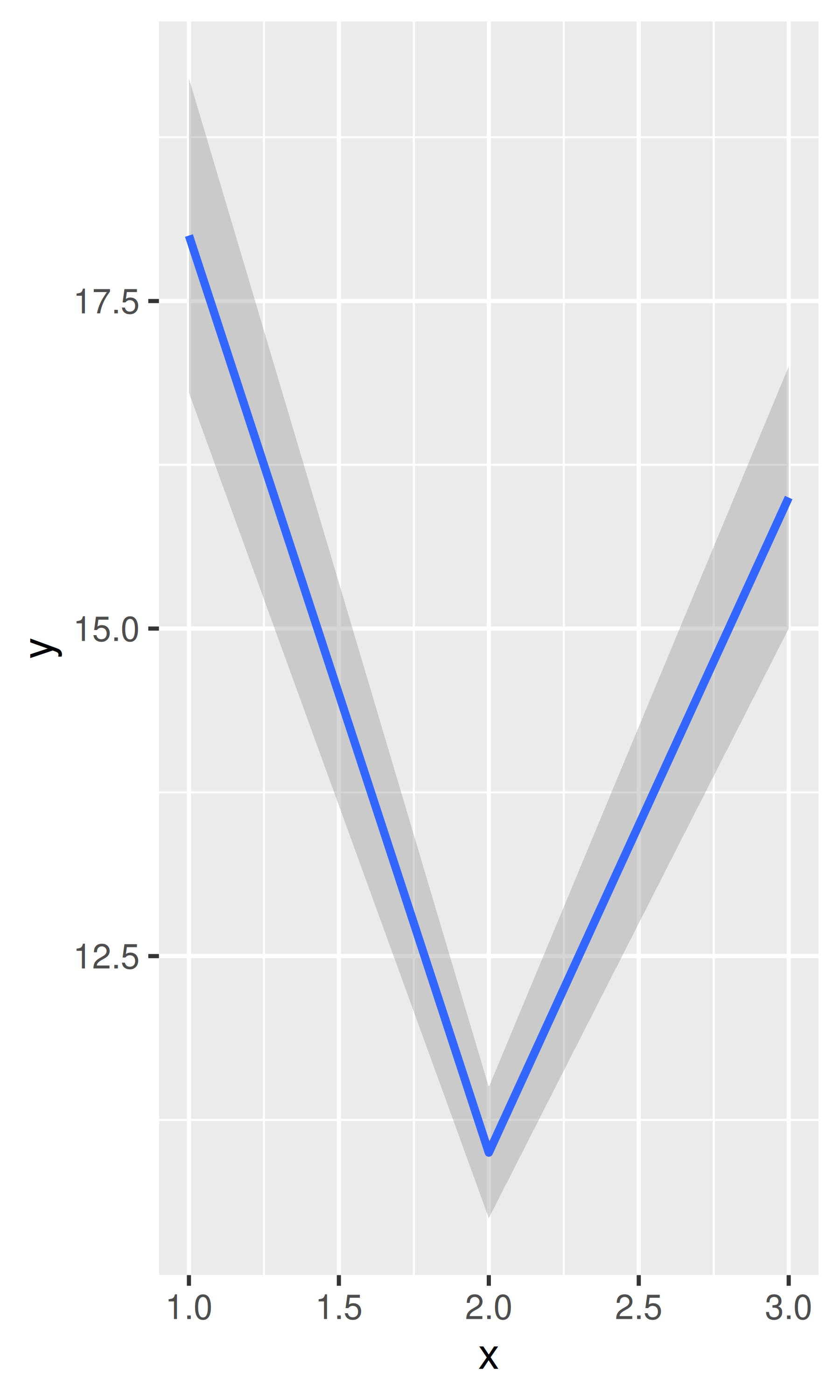
base + geom_smooth(stat = "identity")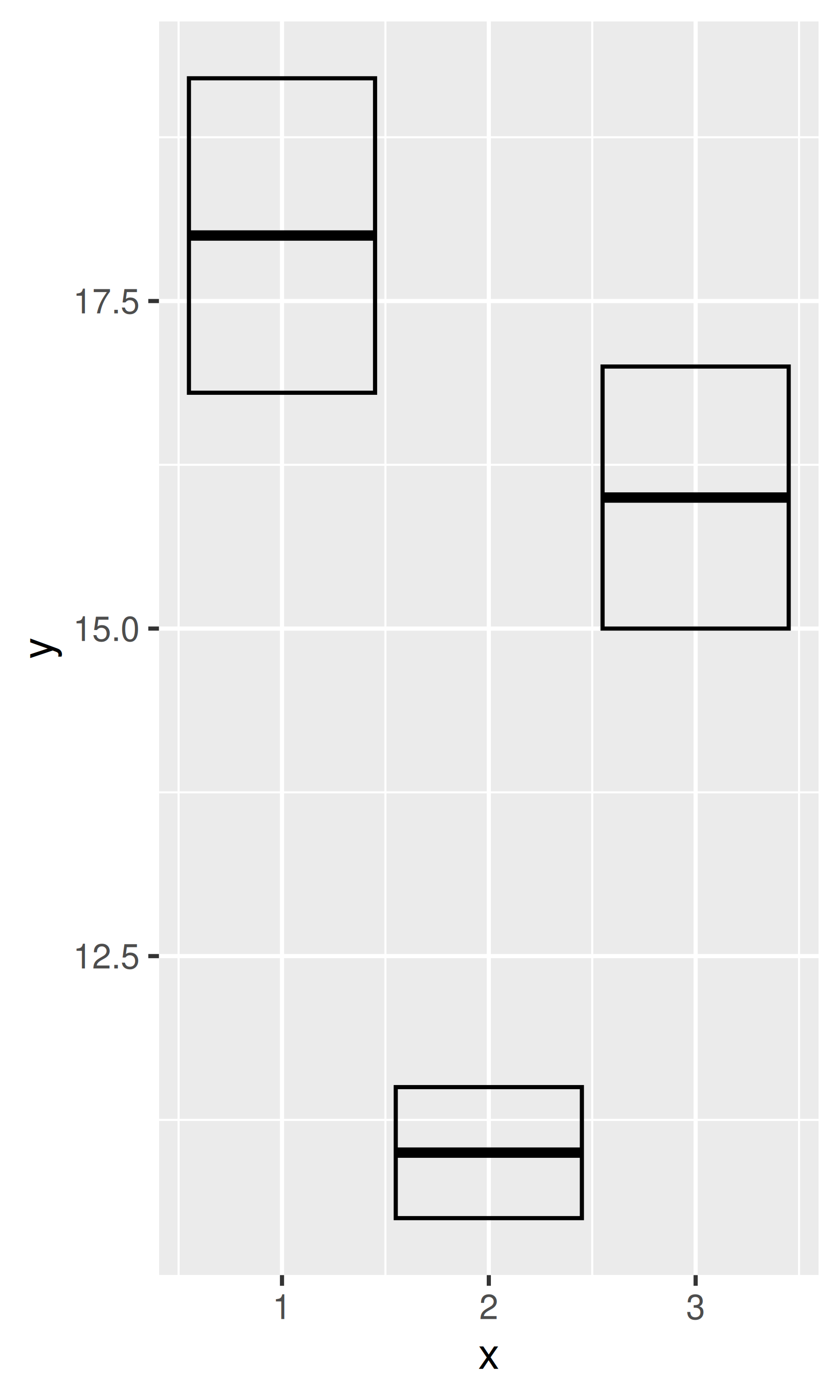
base + geom_errorbar()
base + geom_linerange()
base + geom_ribbon()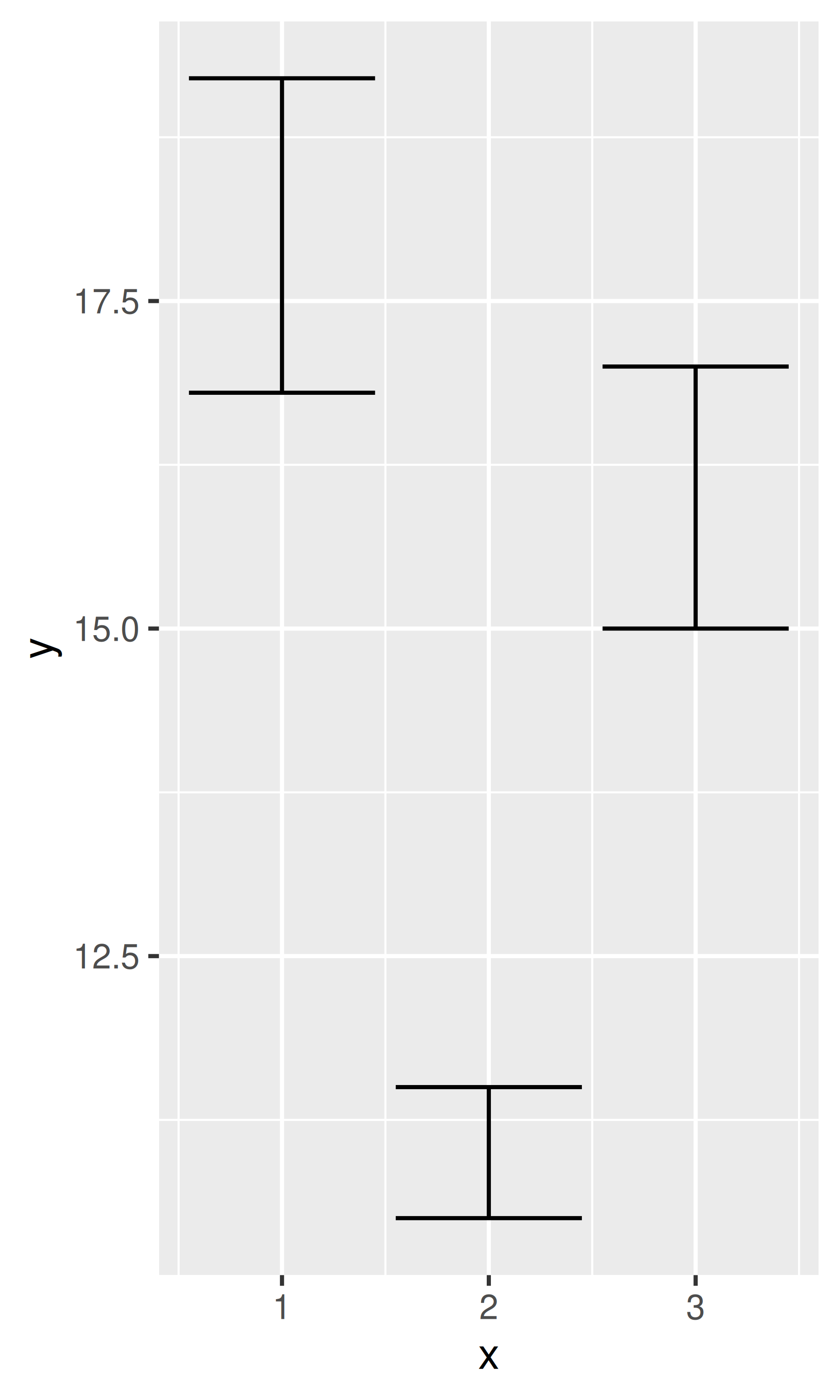
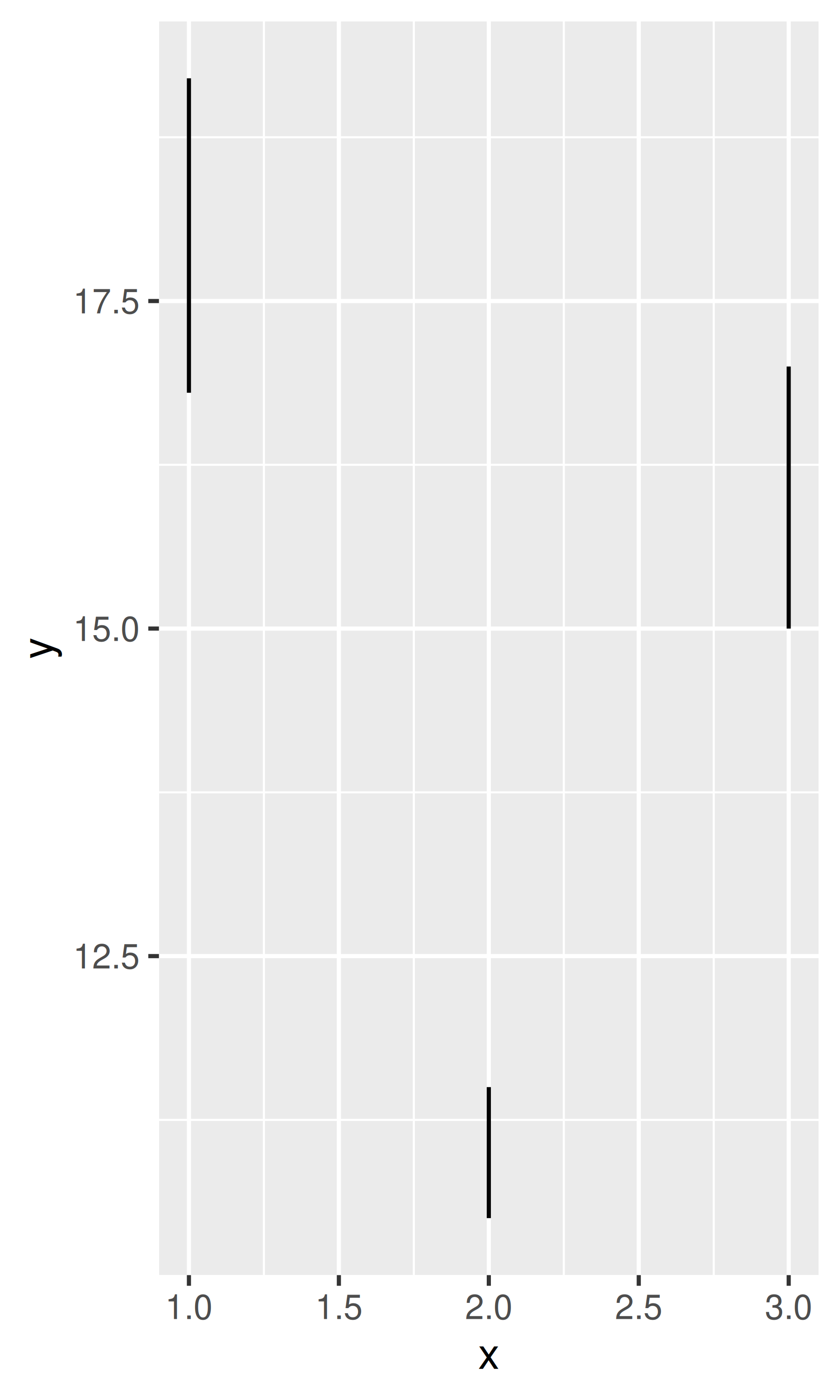
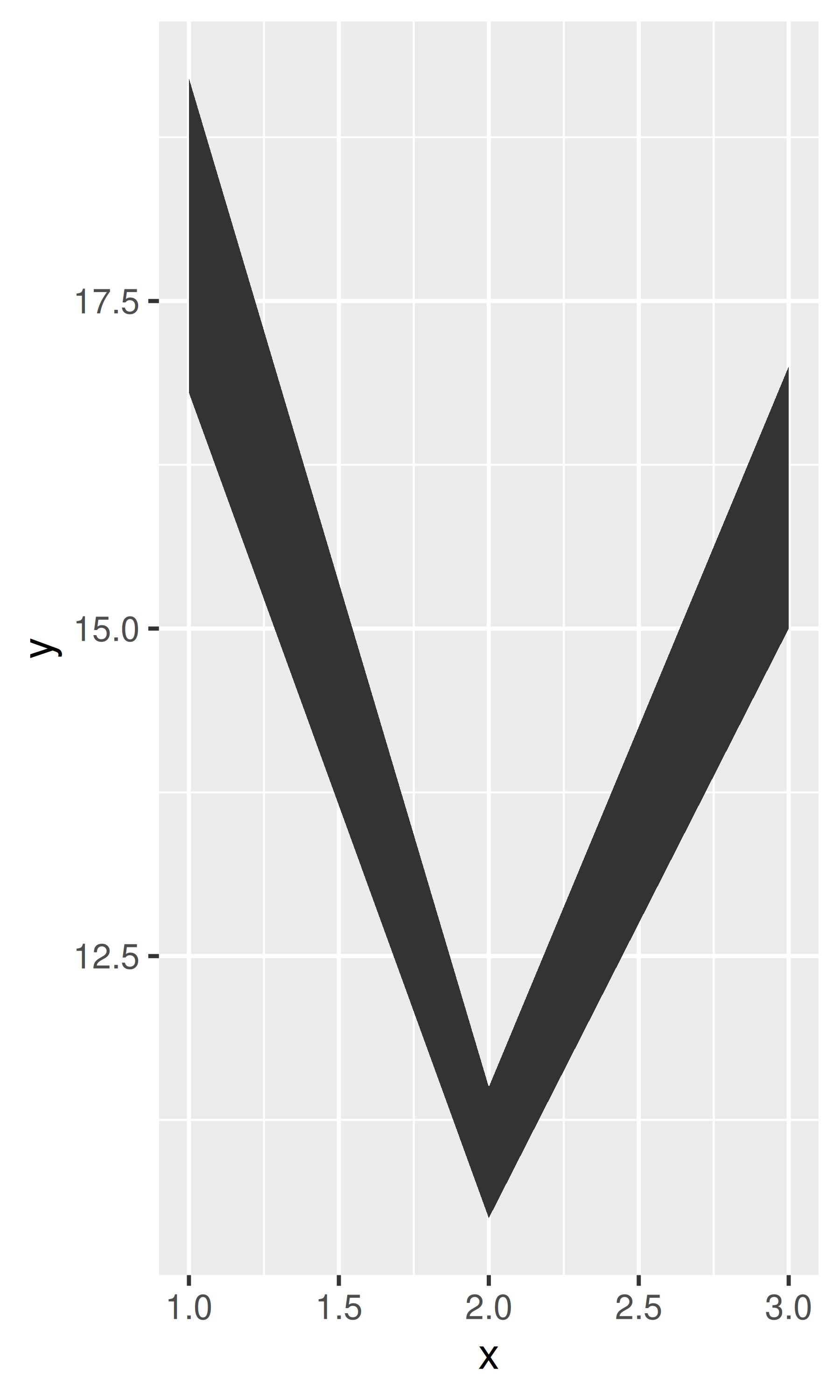
Debido a que hay tantas formas diferentes de calcular los errores estándar, el cálculo depende de usted. Para casos muy simples, ggplot2 proporciona algunas herramientas en forma de funciones de resumen que se describen a continuación; de lo contrario, tendrá que hacerlo usted mismo.R para la Ciencia de Datos (https://r4ds.had.co.nz) contiene más consejos sobre cómo trabajar con modelos más sofisticados.
5.2 Datos ponderados
Cuando tiene datos agregados donde cada fila del conjunto de datos representa múltiples observaciones, necesita alguna forma de tener en cuenta la variable de ponderación. Usaremos algunos datos recopilados sobre los estados del Medio Oeste en el censo estadounidense de 2000 en el marco de datos incorporado del midwest. Los datos consisten principalmente en porcentajes (por ejemplo, porcentaje de blancos, porcentaje por debajo del umbral de pobreza, porcentaje con título universitario) y cierta información para cada condado (área, población total, densidad de población).
Hay algunas cosas diferentes que quizás queramos considerar:
- Nada, para mirar el número de condados.
- Población total, para trabajar con números absolutos.
- Área, para investigar efectos geográficos. (Esto no es útil para el
midwest, pero lo sería si tuviéramos variables como el porcentaje de tierras de cultivo).
La elección de una variable de ponderación afecta profundamente lo que estamos viendo en la gráfica y las conclusiones que sacaremos. Hay dos atributos estéticos que se pueden utilizar para ajustar los pesos. En primer lugar, para geoms simples como líneas y puntos, use la estética de tamaño:
# no ponderado
ggplot(midwest, aes(percwhite, percbelowpoverty)) +
geom_point()
# Peso por población
ggplot(midwest, aes(percwhite, percbelowpoverty)) +
geom_point(aes(size = poptotal / 1e6)) +
scale_size_area("Población\n(millones)", breaks = c(0.5, 1, 2, 4))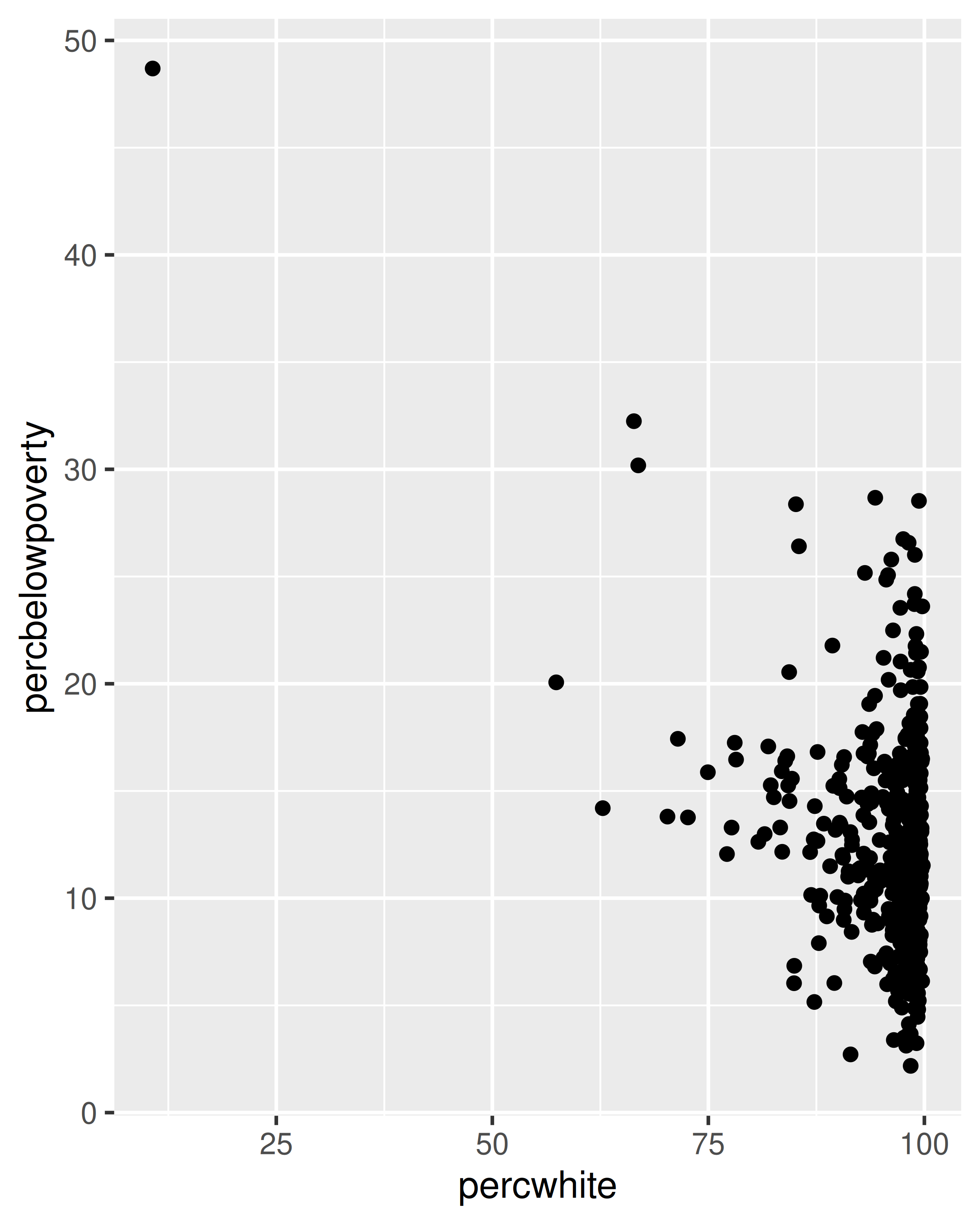
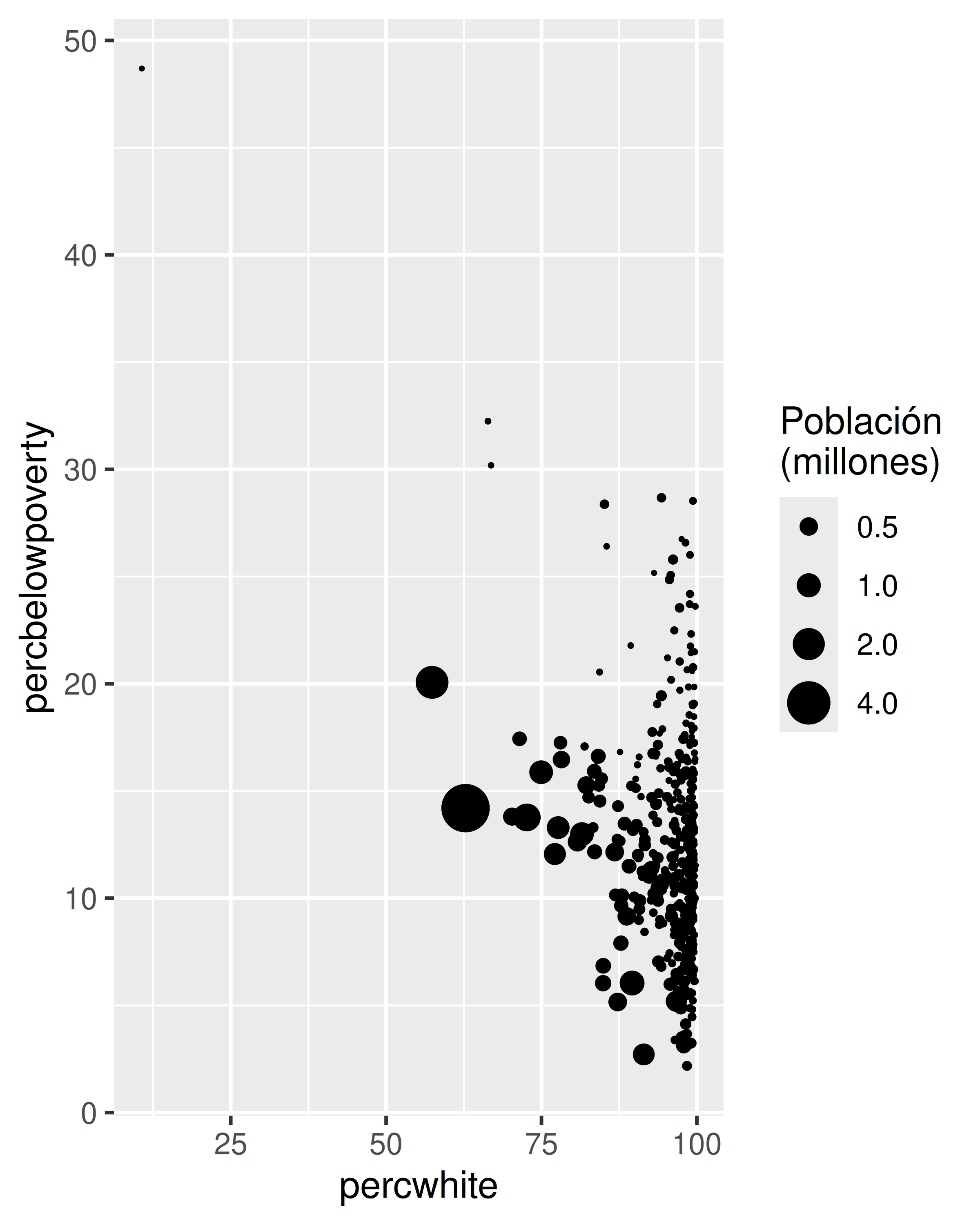
Para geomas más complicadas que implican alguna transformación estadística, especificamos pesos con la estética weight. Estos pesos se pasarán a la función de resumen estadístico. Se admiten ponderaciones para todos los casos en los que tenga sentido: suavizadores, regresiones cuantiles, diagramas de caja, histogramas y diagramas de densidad. No puede ver esta variable de ponderación directamente y no produce una leyenda, pero cambiará los resultados del resumen estadístico. El siguiente código muestra cómo la ponderación por densidad de población afecta la relación entre el porcentaje de blancos y el porcentaje por debajo del umbral de pobreza.
# no ponderado
ggplot(midwest, aes(percwhite, percbelowpoverty)) +
geom_point() +
geom_smooth(method = lm, linewidth = 1)
#> `geom_smooth()` using formula = 'y ~ x'
# Ponderado por población
ggplot(midwest, aes(percwhite, percbelowpoverty)) +
geom_point(aes(size = poptotal / 1e6)) +
geom_smooth(aes(weight = poptotal), method = lm, linewidth = 1) +
scale_size_area(guide = "none")
#> `geom_smooth()` using formula = 'y ~ x'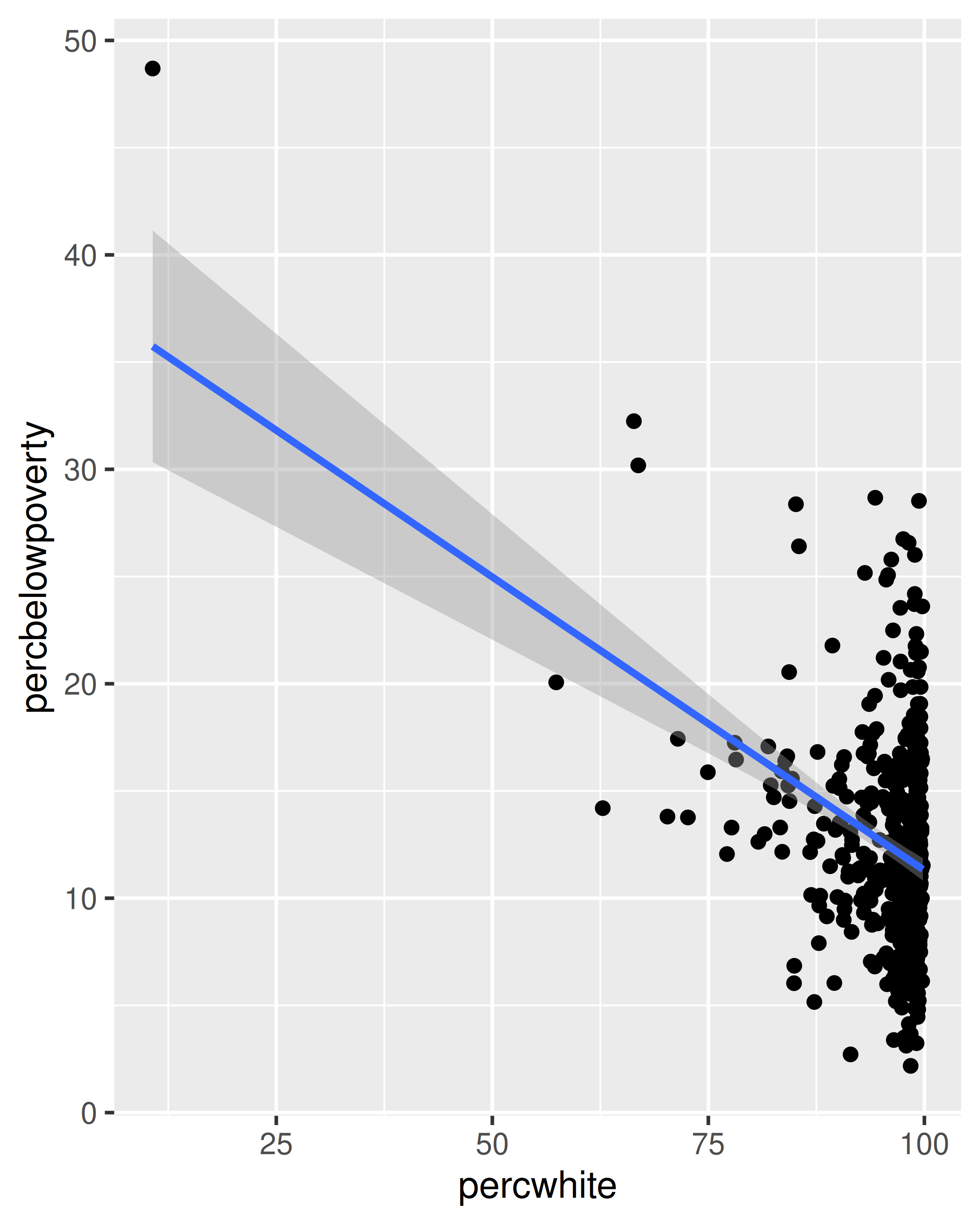
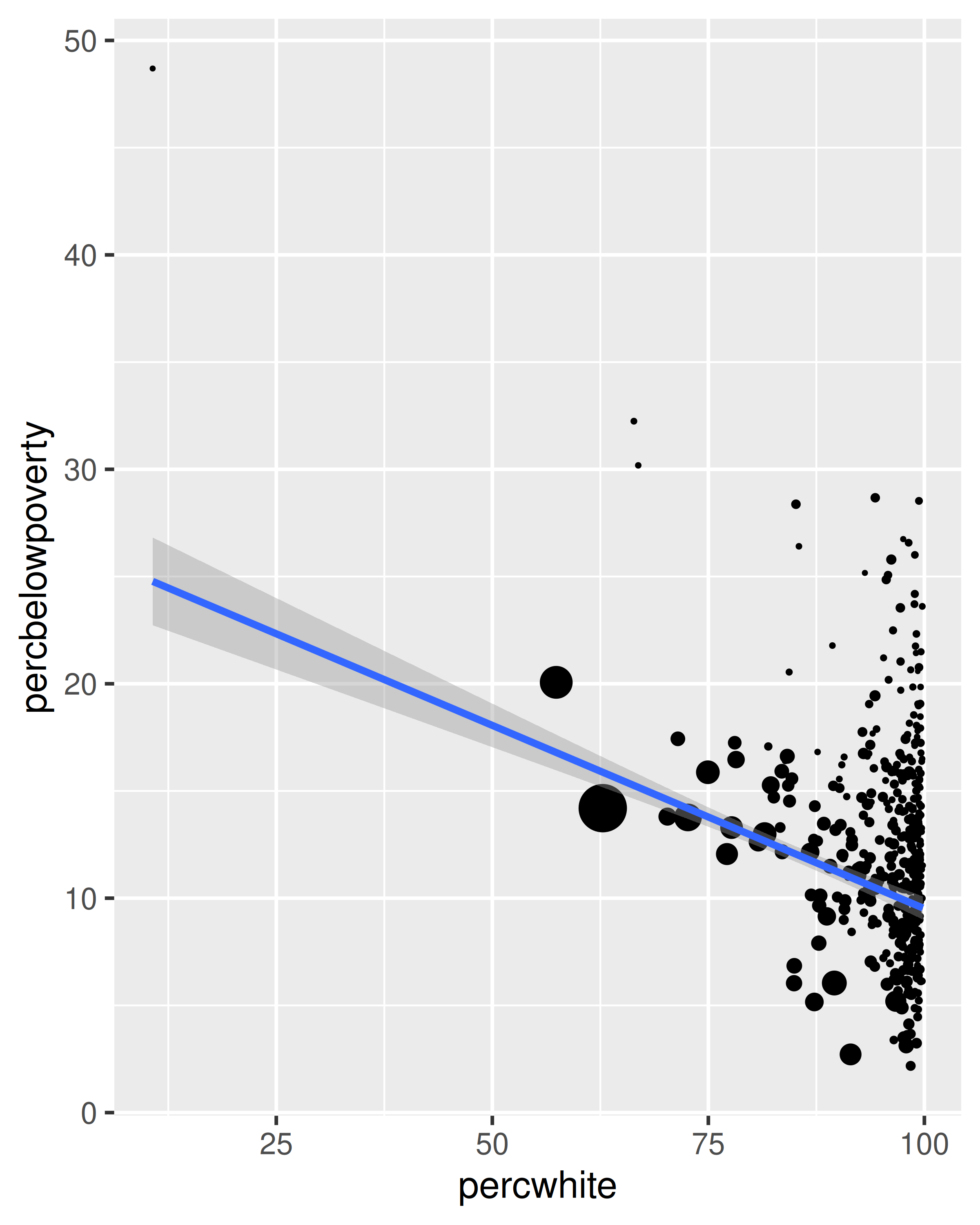
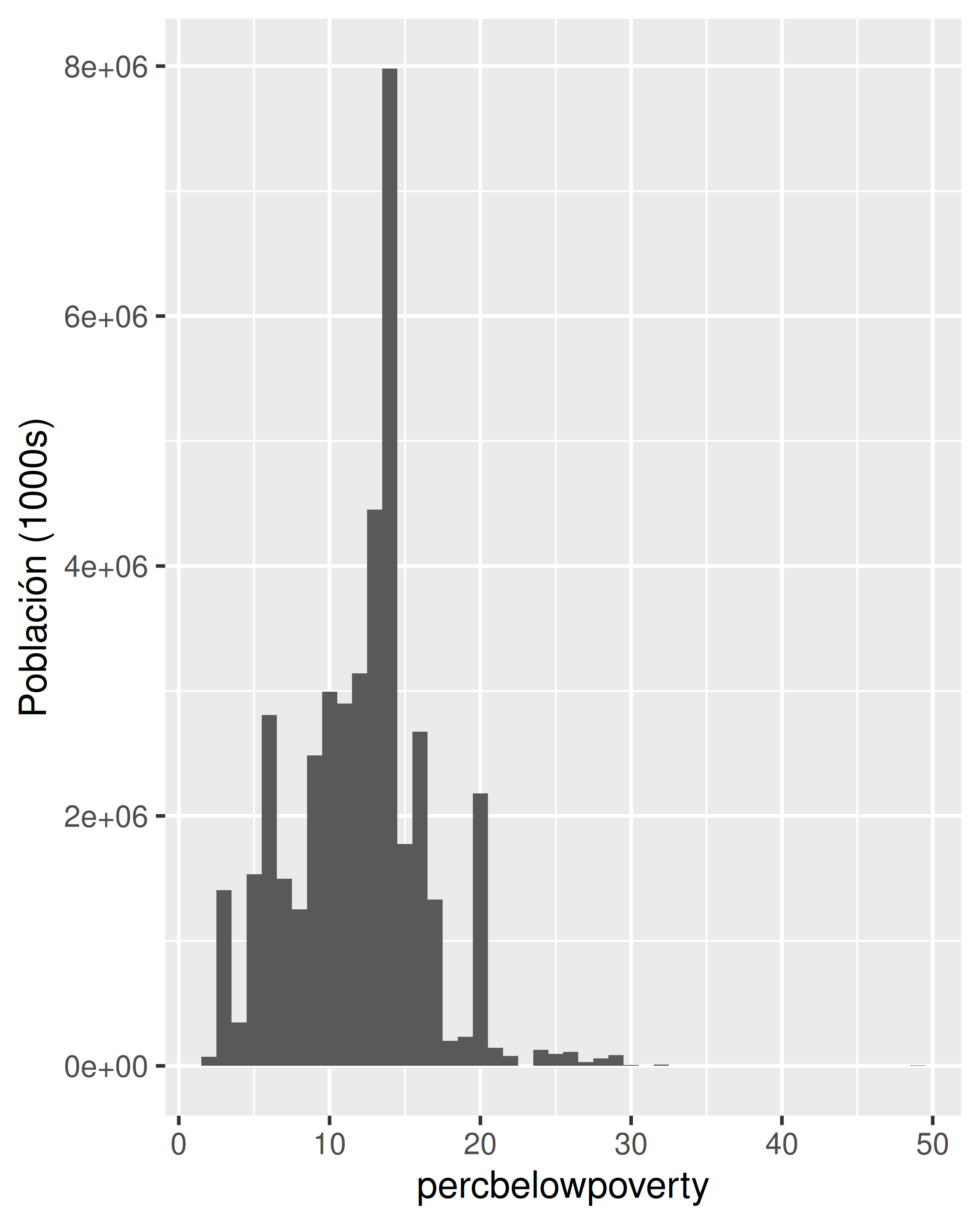
Cuando ponderamos un histograma o un gráfico de densidad por la población total, pasamos de observar la distribución del número de condados a la distribución del número de personas. El siguiente código muestra la diferencia que esto supone para un histograma del porcentaje por debajo del umbral de pobreza:
ggplot(midwest, aes(percbelowpoverty)) +
geom_histogram(binwidth = 1) +
ylab("Condados")
ggplot(midwest, aes(percbelowpoverty)) +
geom_histogram(aes(weight = poptotal), binwidth = 1) +
ylab("Población (1000s)")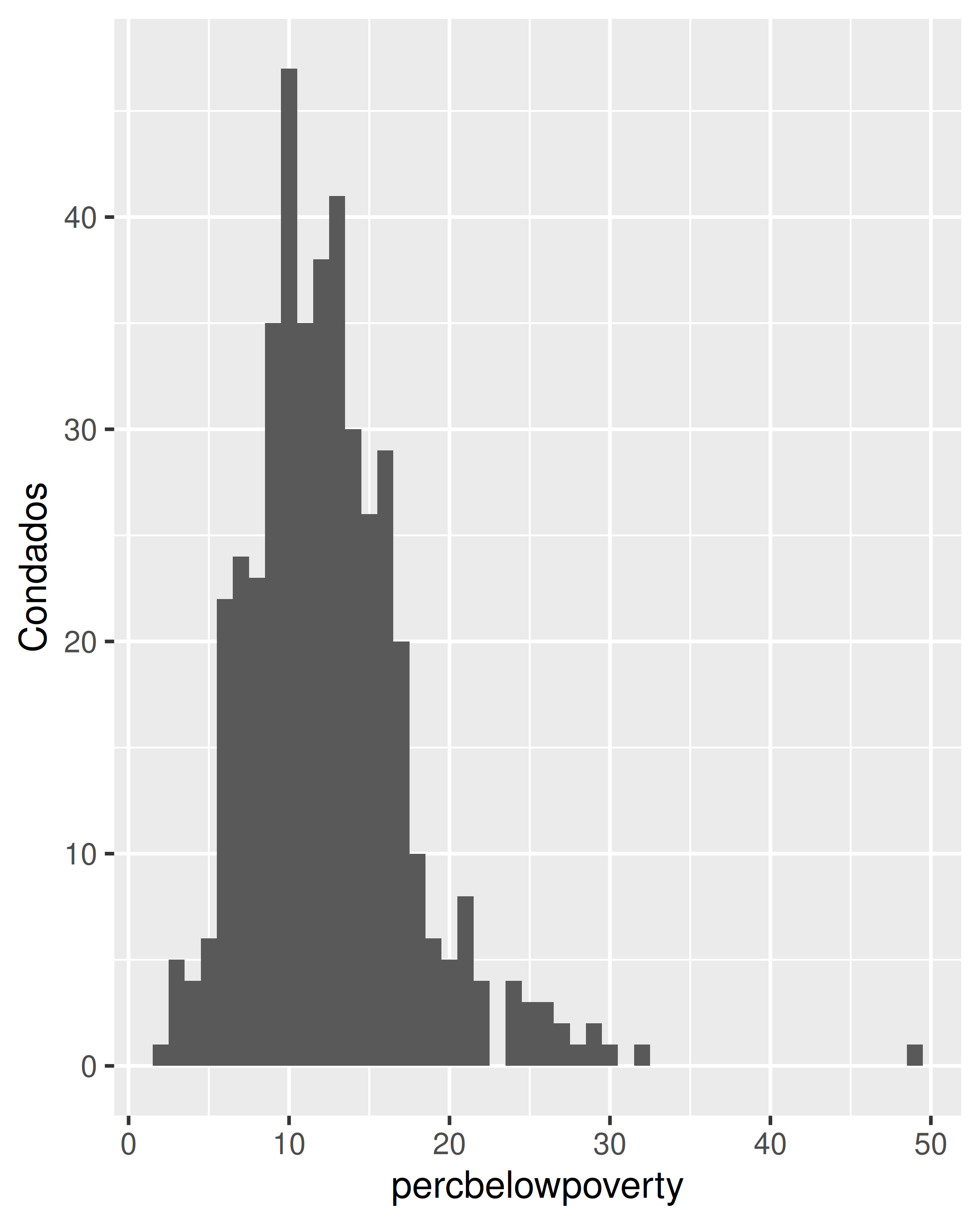
5.3 Datos de diamantes
Para demostrar herramientas para grandes conjuntos de datos, usaremos el conjunto de datos integrado diamonds, que consta de información de precio y calidad para ~54,000 diamantes:
Los datos contienen las cuatro C de la calidad del diamante: quilates, talla, color y claridad; y cinco medidas físicas: profundidad, tabla, x, y y z, como se describe en la siguiente figura.
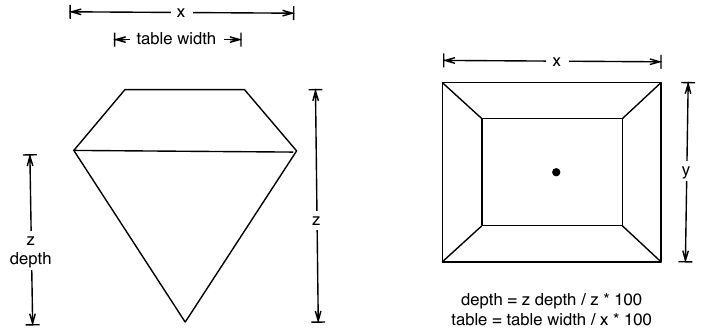
El conjunto de datos no se ha limpiado bien, por lo que, además de demostrar datos interesantes sobre los diamantes, también muestra algunos problemas de calidad de los datos.
5.4 Mostrando distribuciones
Hay una serie de geoms que se pueden usar para mostrar distribuciones, dependiendo de la dimensionalidad de la distribución, si es continua o discreta, y si está interesado en la distribución condicional o conjunta.
Para distribuciones continuas 1d, la geom más importante es el histograma, geom_histogram():
ggplot(diamonds, aes(depth)) +
geom_histogram()
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
ggplot(diamonds, aes(depth)) +
geom_histogram(binwidth = 0.1) +
xlim(55, 70)
#> Warning: Removed 45 rows containing non-finite outside the scale range
#> (`stat_bin()`).
#> Warning: Removed 2 rows containing missing values or values outside the scale range
#> (`geom_bar()`).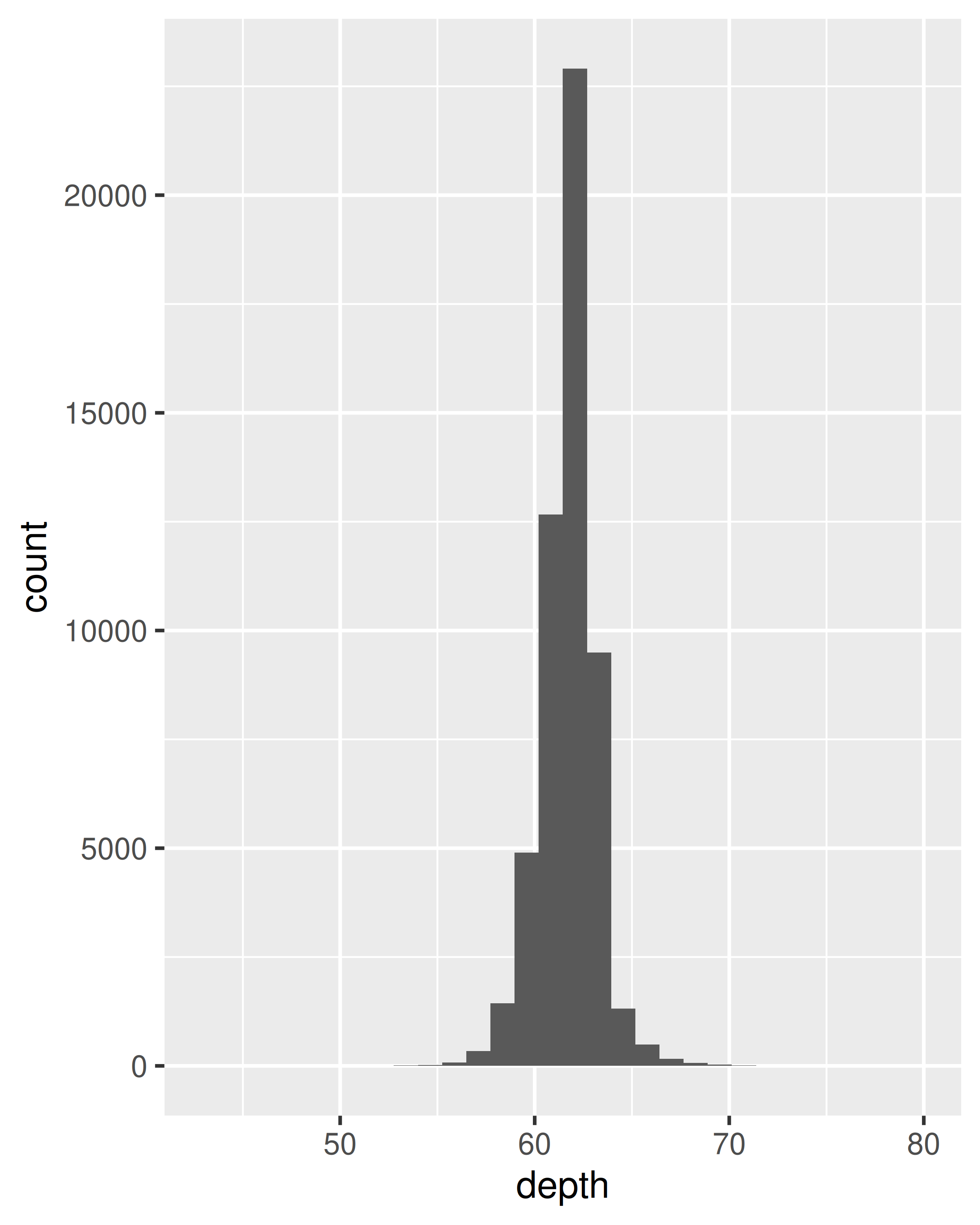
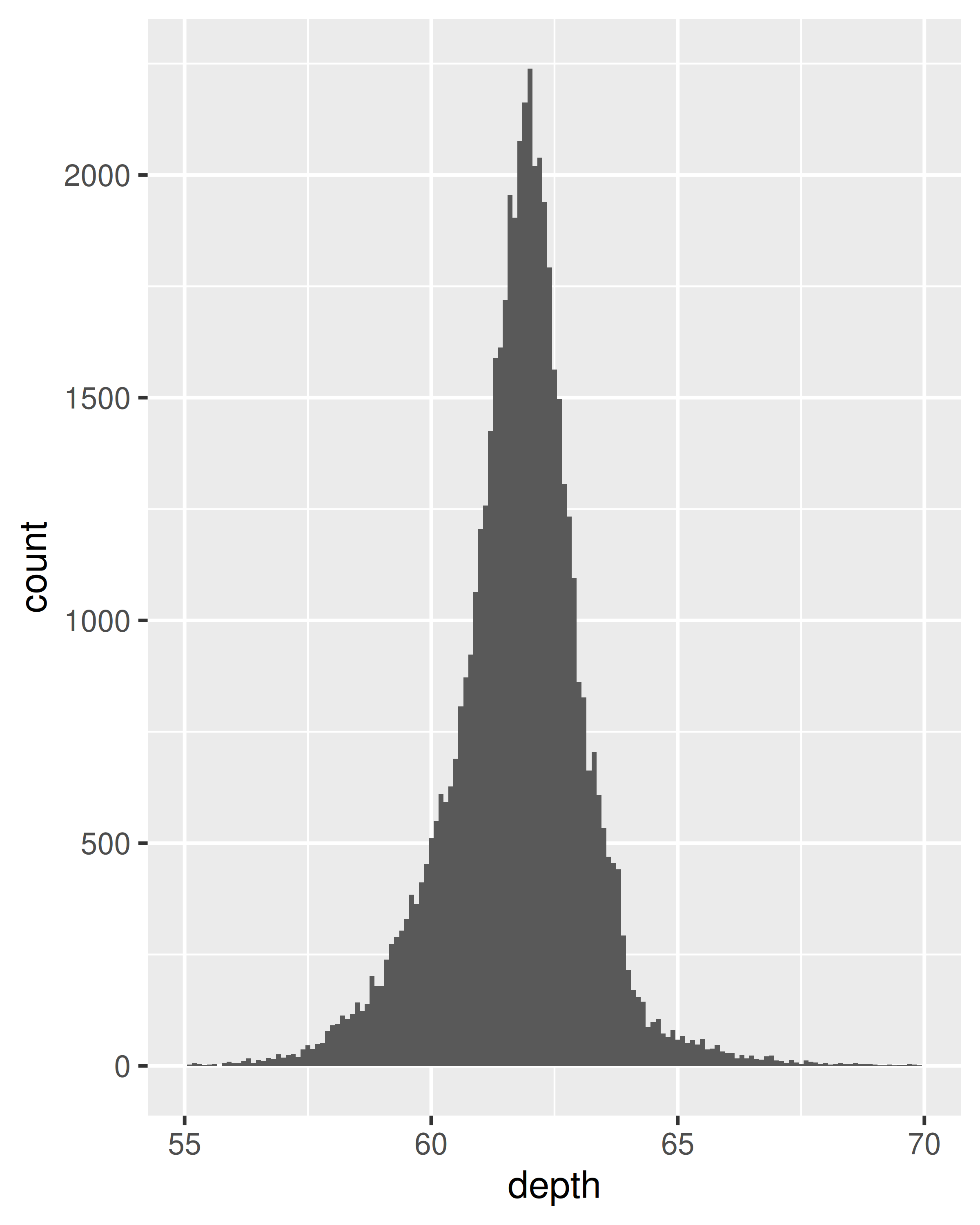
Es importante experimentar con la agrupación para encontrar una vista reveladora. Puede cambiar el binwidth, especificar el número de bins o especificar la ubicación exacta de los breaks. Nunca confíe en los parámetros predeterminados para obtener una vista reveladora de la distribución. Hacer zoom en el eje x, xlim(55, 70), y seleccionar un ancho de contenedor más pequeño, binwidth = 0.1, revela muchos más detalles.
Al publicar cifras, no olvide incluir información sobre parámetros importantes (como el ancho del contenedor) en el título.
Si desea comparar la distribución entre grupos, tiene algunas opciones:
- Mostrar pequeños múltiplos del histograma,
facet_wrap(~ var). - Usa color y un polígono de frecuencia,
geom_freqpoly(). - Utilice un “gráfico de densidad condicional”,
geom_histogram(position = "fill").
Los gráficos de polígono de frecuencia y densidad condicional se muestran a continuación. El gráfico de densidad condicional utiliza position_fill() para apilar cada contenedor y escalarlo a la misma altura. Este gráfico es un desafío desde el punto de vista perceptivo porque es necesario comparar las alturas de las barras, no las posiciones, pero se pueden ver los patrones más fuertes.
ggplot(diamonds, aes(depth)) +
geom_freqpoly(aes(colour = cut), binwidth = 0.1, na.rm = TRUE) +
xlim(58, 68) +
theme(legend.position = "none")
ggplot(diamonds, aes(depth)) +
geom_histogram(aes(fill = cut), binwidth = 0.1, position = "fill",
na.rm = TRUE) +
xlim(58, 68) +
theme(legend.position = "none")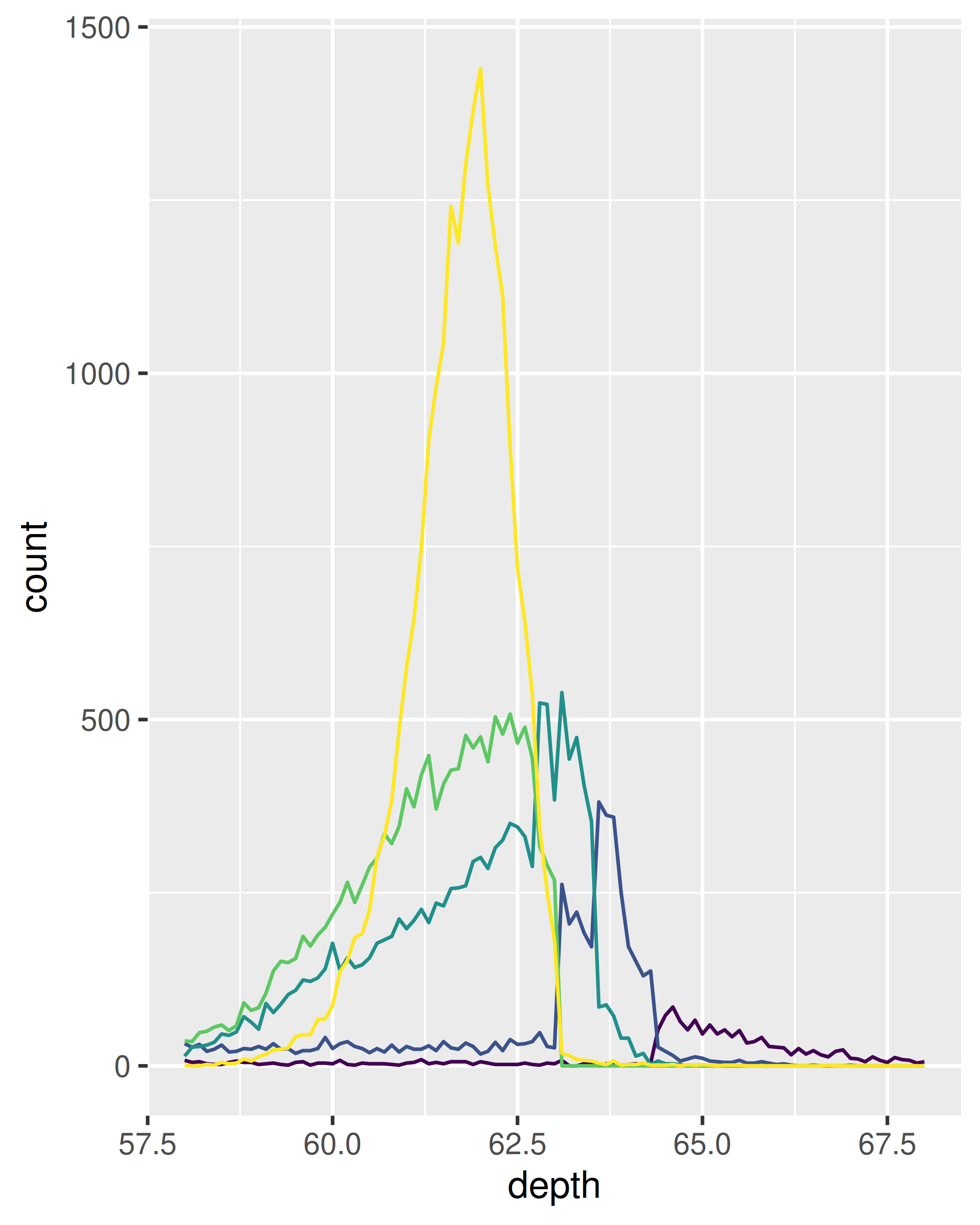
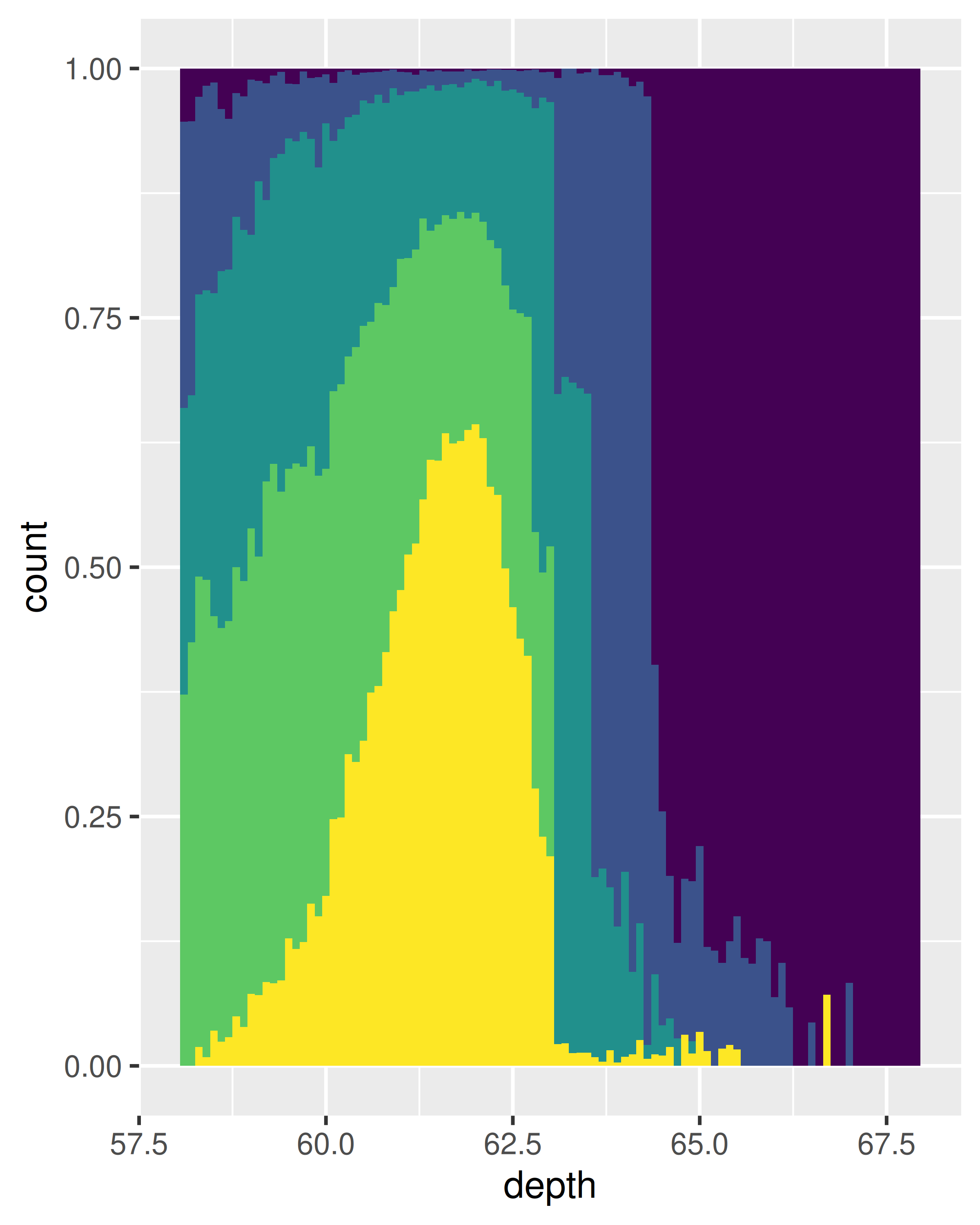
(Hemos suprimido las leyendas para centrarnos en la visualización de los datos).
Tanto el histograma como el polígono de frecuencia utilizan la misma transformación estadística subyacente: stat = "bin". Esta estadística produce dos variables de salida: count y density. De forma predeterminada, el recuento se asigna a la posición y, porque es más interpretable. La densidad es el recuento dividido por el recuento total multiplicado por el ancho del contenedor y es útil cuando desea comparar la forma de las distribuciones, no el tamaño general.
Una alternativa a una visualización basada en contenedores es una estimación de densidad. geom_density() coloca una pequeña distribución normal en cada punto de datos y resume todas las curvas. Tiene propiedades teóricas deseables, pero es más difícil relacionarlo con los datos. Utilice un gráfico de densidad cuando sepa que la densidad subyacente es suave, continua e ilimitada. Puede utilizar el parámetro adjust para hacer que la densidad sea más o menos suave.
ggplot(diamonds, aes(depth)) +
geom_density(na.rm = TRUE) +
xlim(58, 68) +
theme(legend.position = "none")
ggplot(diamonds, aes(depth, fill = cut, colour = cut)) +
geom_density(alpha = 0.2, na.rm = TRUE) +
xlim(58, 68) +
theme(legend.position = "none")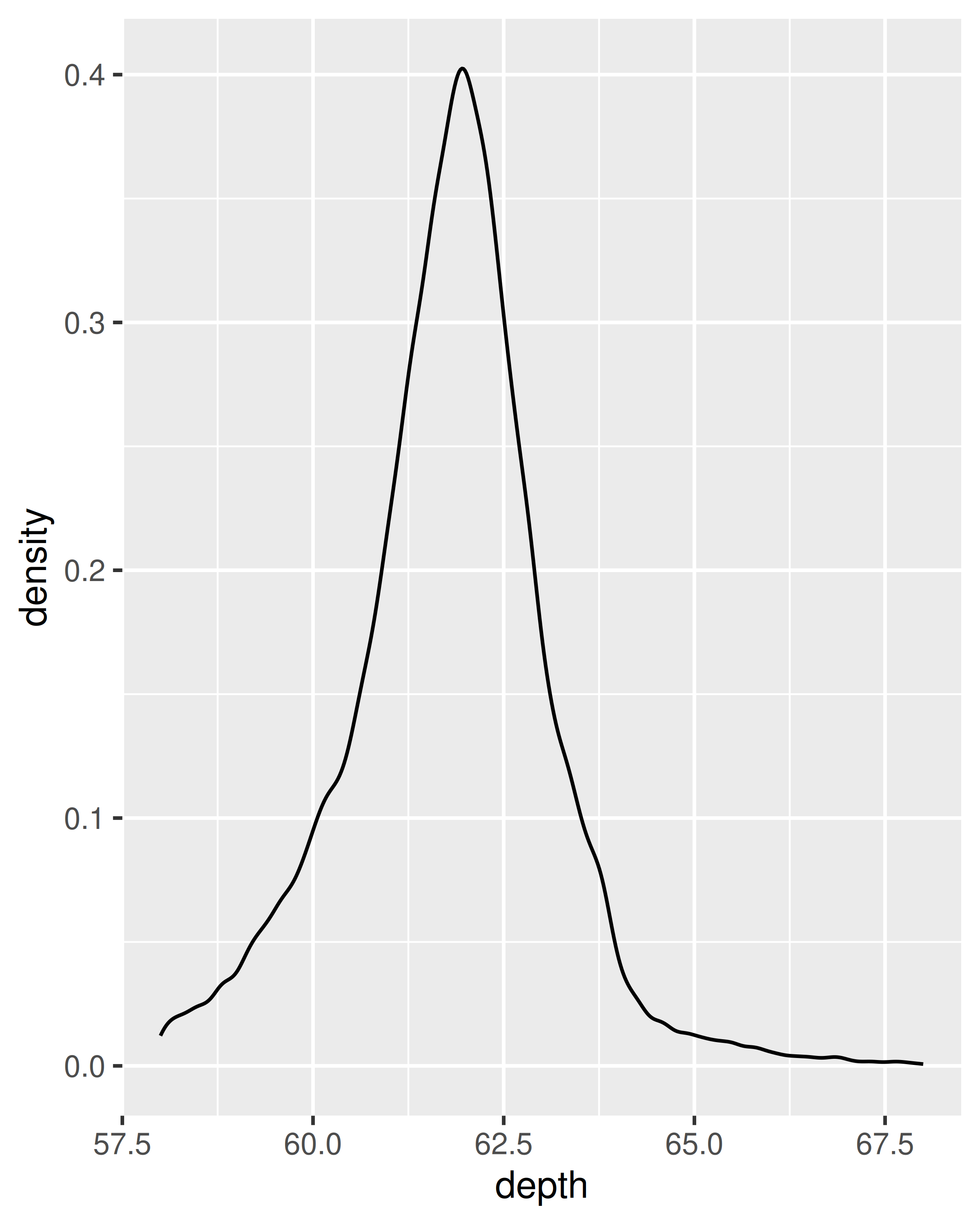
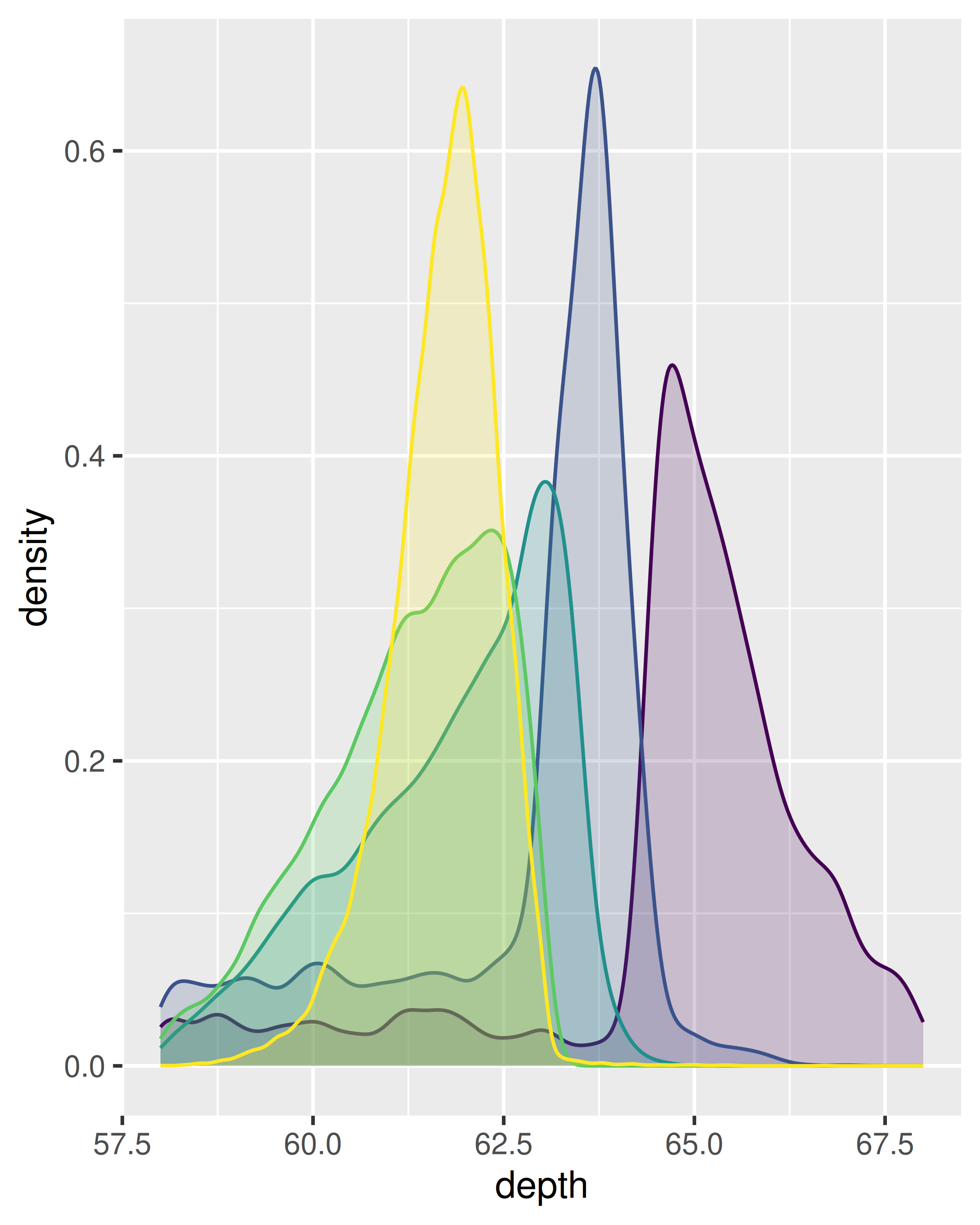
Tenga en cuenta que el área de cada estimación de densidad está estandarizada a uno, por lo que se pierde información sobre el tamaño relativo de cada grupo.
El histograma, el polígono de frecuencia y la densidad muestran una vista detallada de la distribución. Sin embargo, a veces quieres comparar muchas distribuciones y es útil tener opciones alternativas que sacrifiquen calidad por cantidad. Aquí hay tres opciones:
-
geom_boxplot(): el diagrama de caja y bigotes muestra cinco estadísticas resumidas junto con “valores atípicos” individuales. Muestra mucha menos información que un histograma, pero también ocupa mucho menos espacio.Puede utilizar un diagrama de caja con x tanto categórica como continua. Para x continuo, también deberá configurar la estética del grupo para definir cómo se divide la variable x en contenedores. Una función auxiliar útil es
cut_width():ggplot(diamonds, aes(clarity, depth)) + geom_boxplot() ggplot(diamonds, aes(carat, depth)) + geom_boxplot(aes(group = cut_width(carat, 0.1))) + xlim(NA, 2.05) #> Warning: Removed 997 rows containing missing values or values outside the scale range #> (`stat_boxplot()`).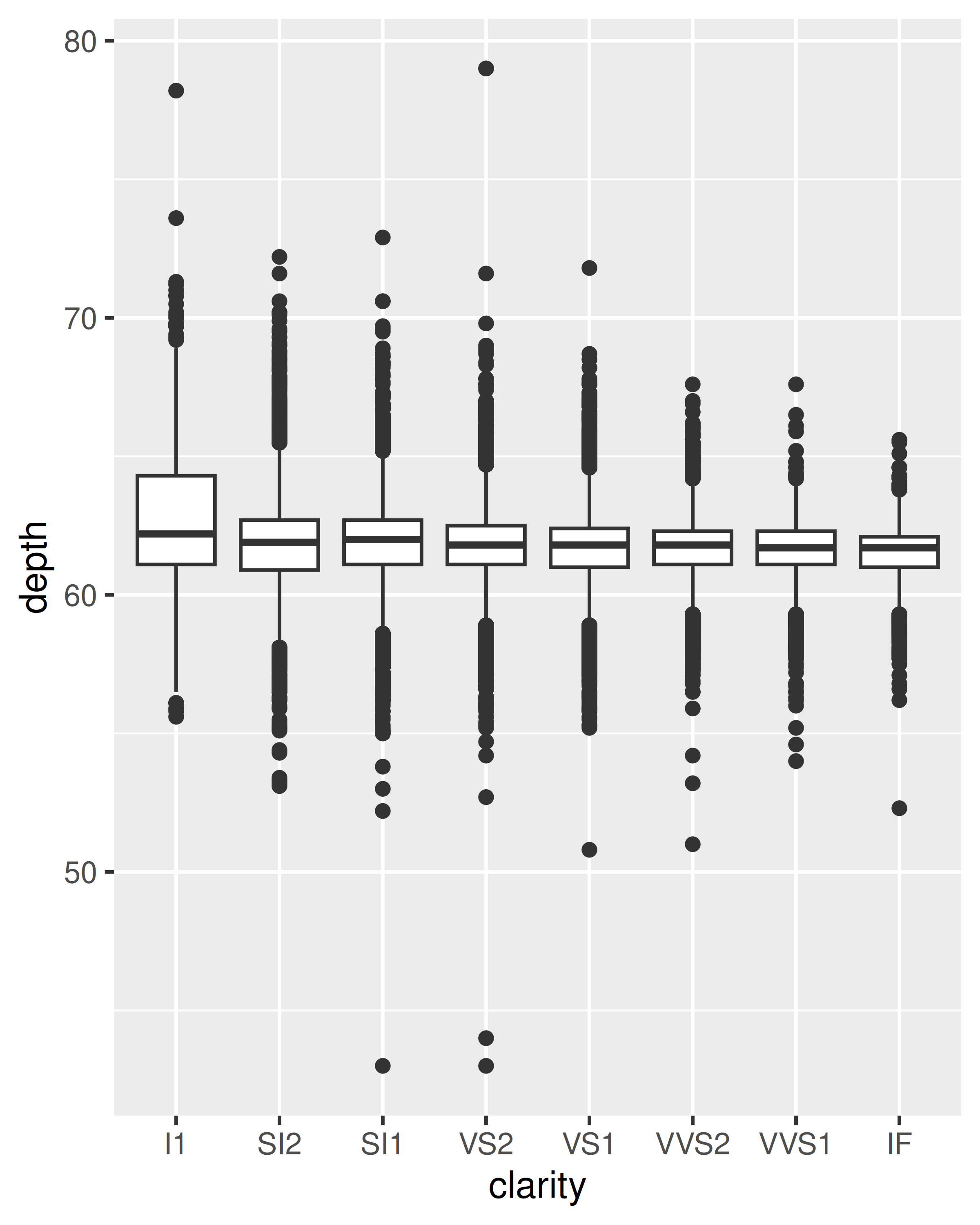
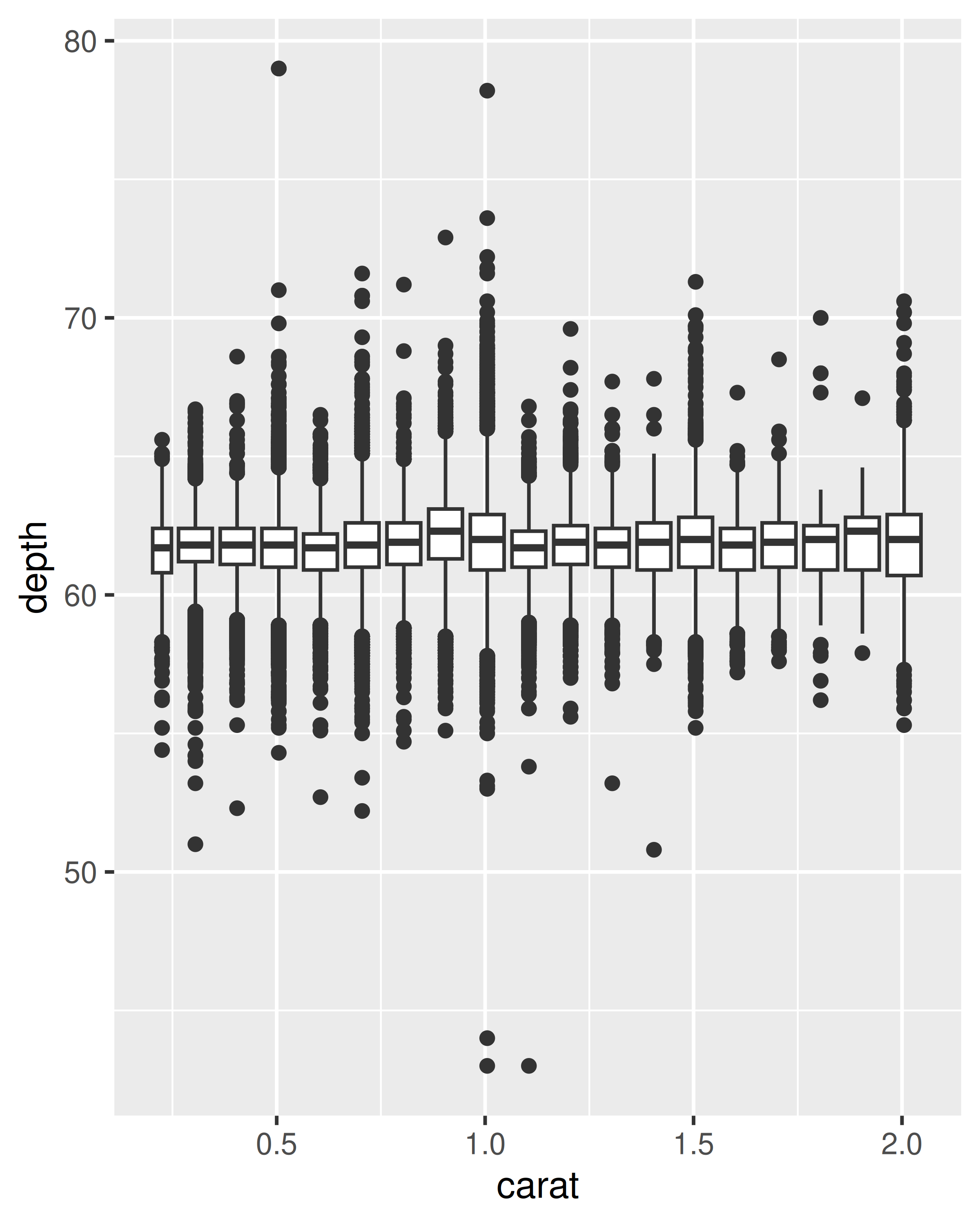
-
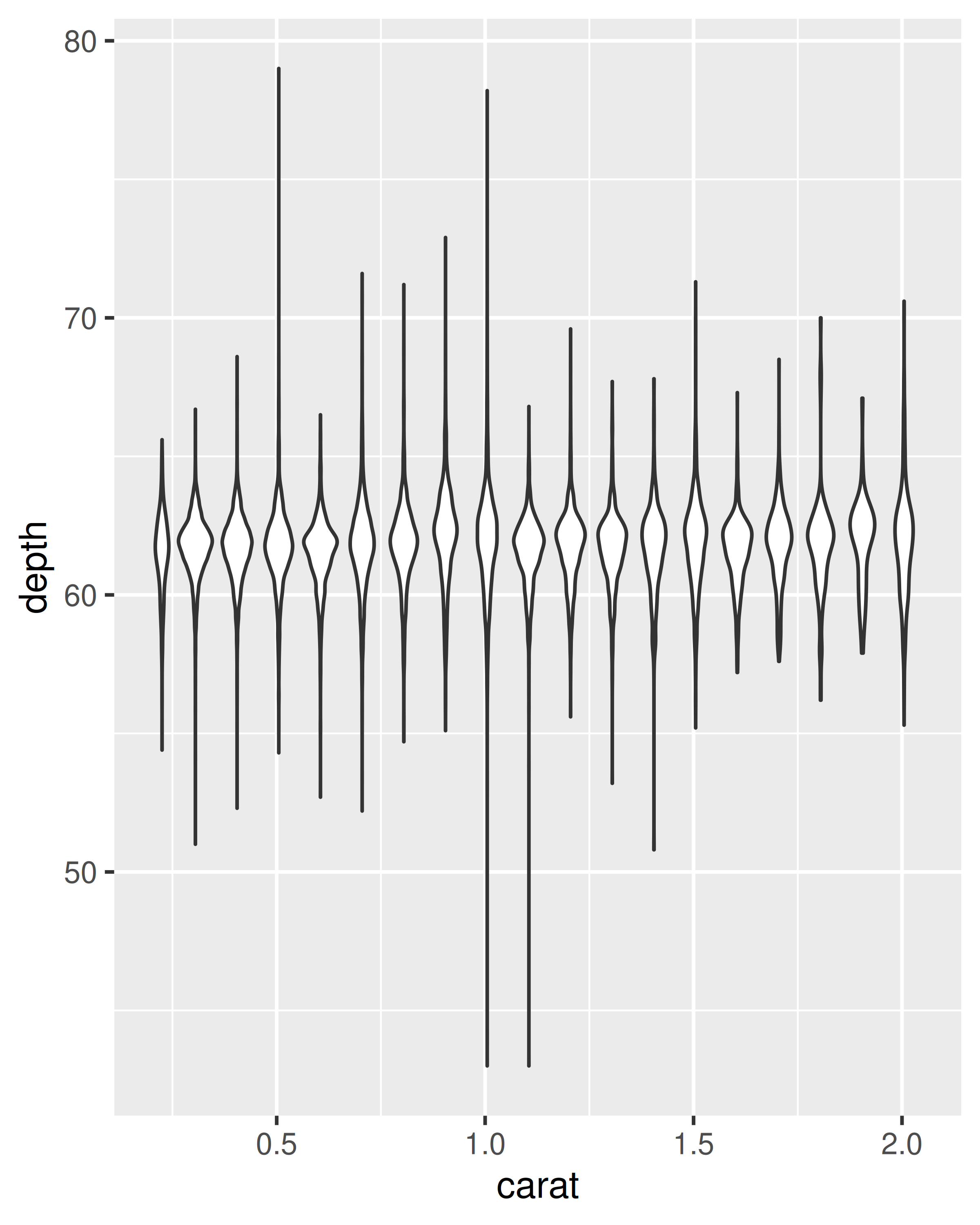
geom_violin(): el diagrama del violín es una versión compacta del diagrama de densidad. El cálculo subyacente es el mismo, pero los resultados se muestran de forma similar al diagrama de caja:ggplot(diamonds, aes(clarity, depth)) + geom_violin() ggplot(diamonds, aes(carat, depth)) + geom_violin(aes(group = cut_width(carat, 0.1))) + xlim(NA, 2.05) #> Warning: Removed 997 rows containing non-finite outside the scale range #> (`stat_ydensity()`).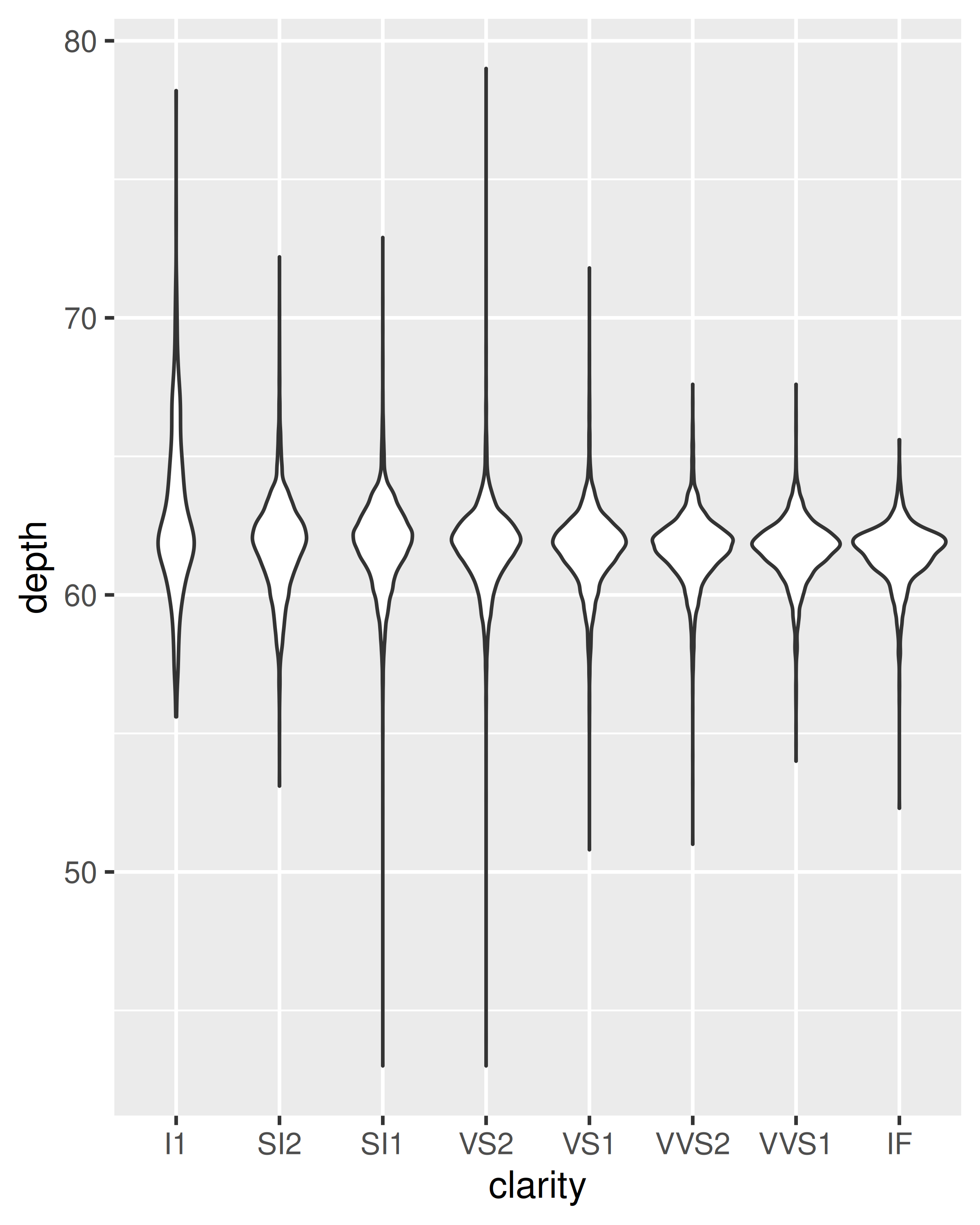
geom_dotplot(): Dibuja un punto para cada observación, cuidadosamente ajustado en el espacio para evitar superposiciones y mostrar la distribución. Es útil para conjuntos de datos más pequeños.
5.4.1 Ejercicios
¿Qué binwidth te cuenta la historia más interesante sobre la distribución de
carat?Dibuja un histograma de
price. ¿Qué patrones interesantes ves?¿Cómo varía la distribución del
priceconclarity?Superponga un polígono de frecuencia y un gráfico de densidad de
depth. ¿Qué variable calculada necesita asignar aypara que los dos gráficos sean comparables? (Puedes modificargeom_freqpoly()ogeom_density().)
5.5 Lidiar con el trazado excesivo
El diagrama de dispersión es una herramienta muy importante para evaluar la relación entre dos variables continuas. Sin embargo, cuando los datos son grandes, los puntos a menudo se trazan uno encima del otro, oscureciendo la verdadera relación. En casos extremos, sólo podrá ver la extensión de los datos y cualquier conclusión que se extraiga del gráfico será sospechosa. Este problema se llama overplotting.
Hay varias formas de abordarlo según el tamaño de los datos y la gravedad del trazado excesivo. El primer conjunto de técnicas implica modificar las propiedades estéticas. Suelen ser más eficaces para conjuntos de datos más pequeños:
-
A veces, se pueden aliviar cantidades muy pequeñas de trazado excesivo haciendo los puntos más pequeños o usando glifos huecos. El siguiente código muestra algunas opciones para 2000 puntos muestreados de una distribución normal bivariada.
df <- data.frame(x = rnorm(2000), y = rnorm(2000)) norm <- ggplot(df, aes(x, y)) + xlab(NULL) + ylab(NULL) norm + geom_point() norm + geom_point(shape = 1) # círculos huecos norm + geom_point(shape = ".") # Tamaño de píxel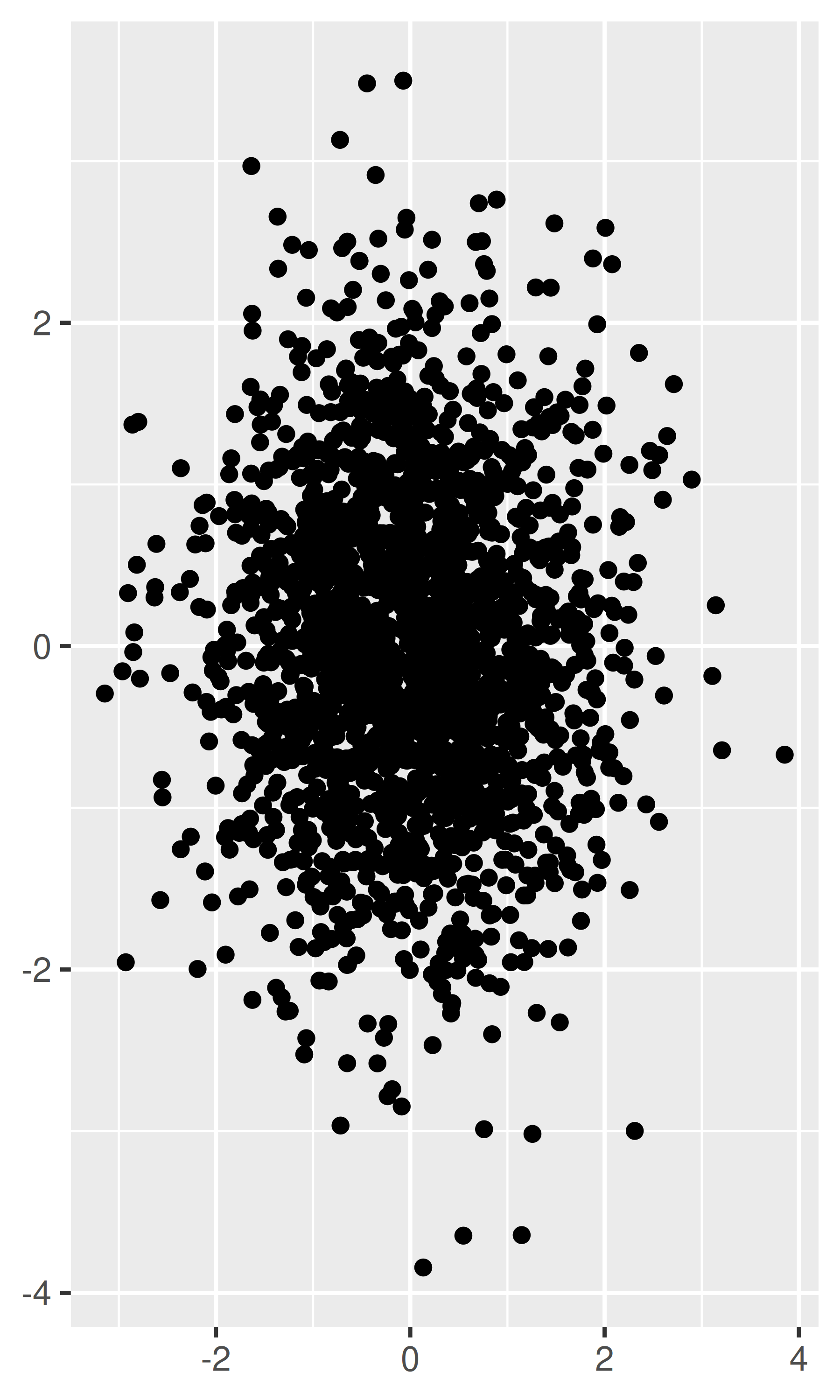
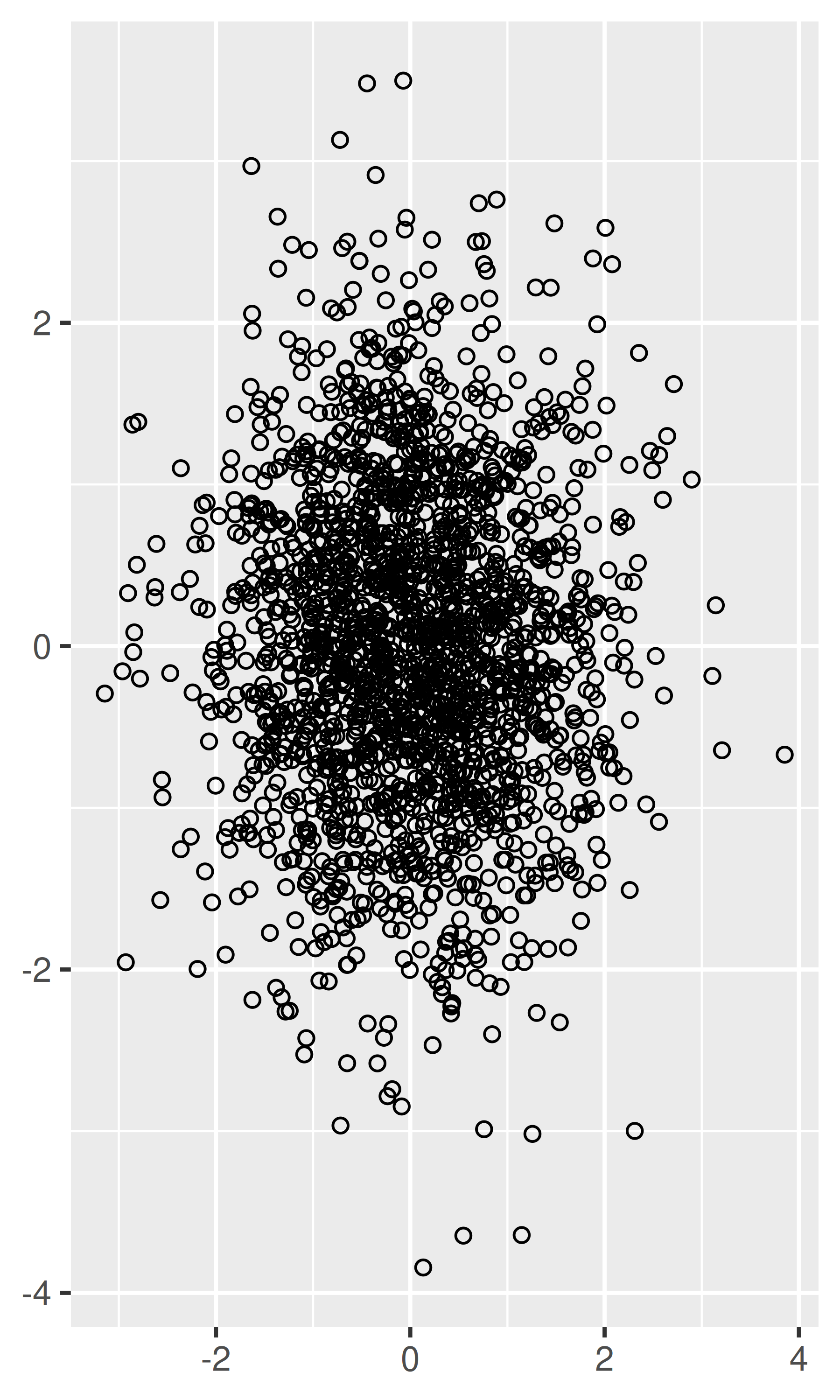
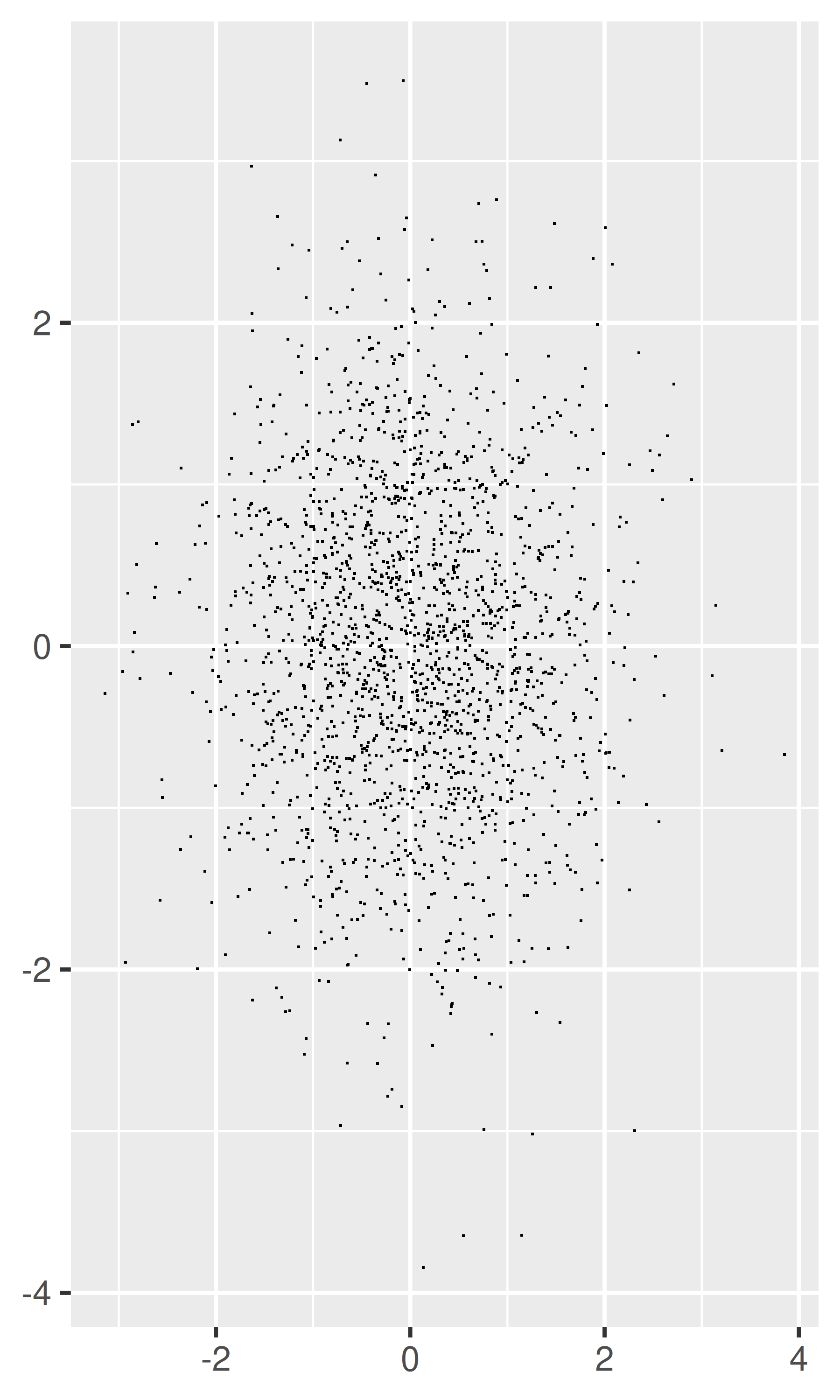
-
Para conjuntos de datos más grandes con más trazados superpuestos, puede utilizar la combinación alfa (transparencia) para hacer que los puntos sean transparentes. Si especifica
alphacomo proporción, el denominador proporciona el número de puntos que se deben superponer para obtener un color sólido. Valores menores que ~\(1/500\) se redondean a cero, dando puntos completamente transparentes.norm + geom_point(alpha = 1 / 3) norm + geom_point(alpha = 1 / 5) norm + geom_point(alpha = 1 / 10)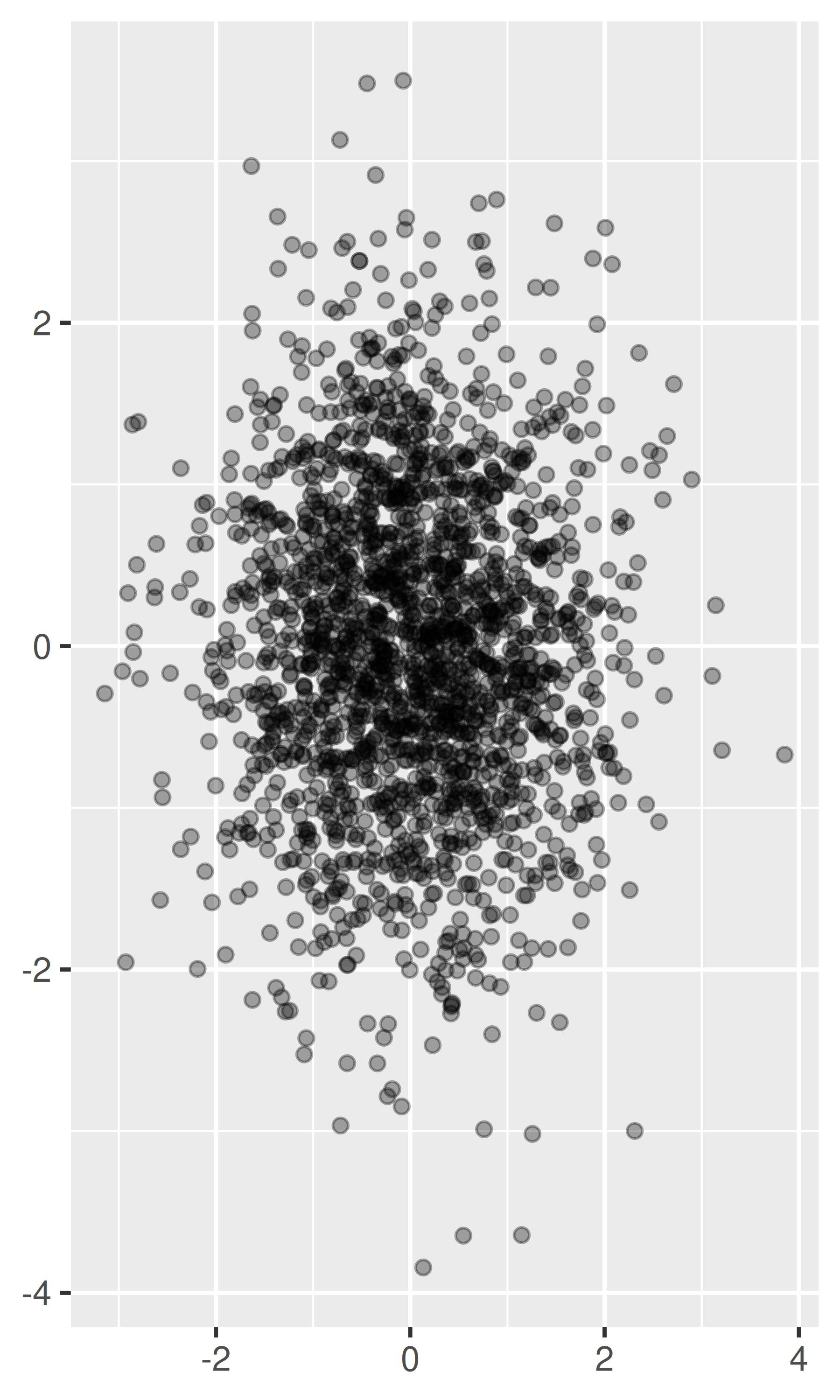
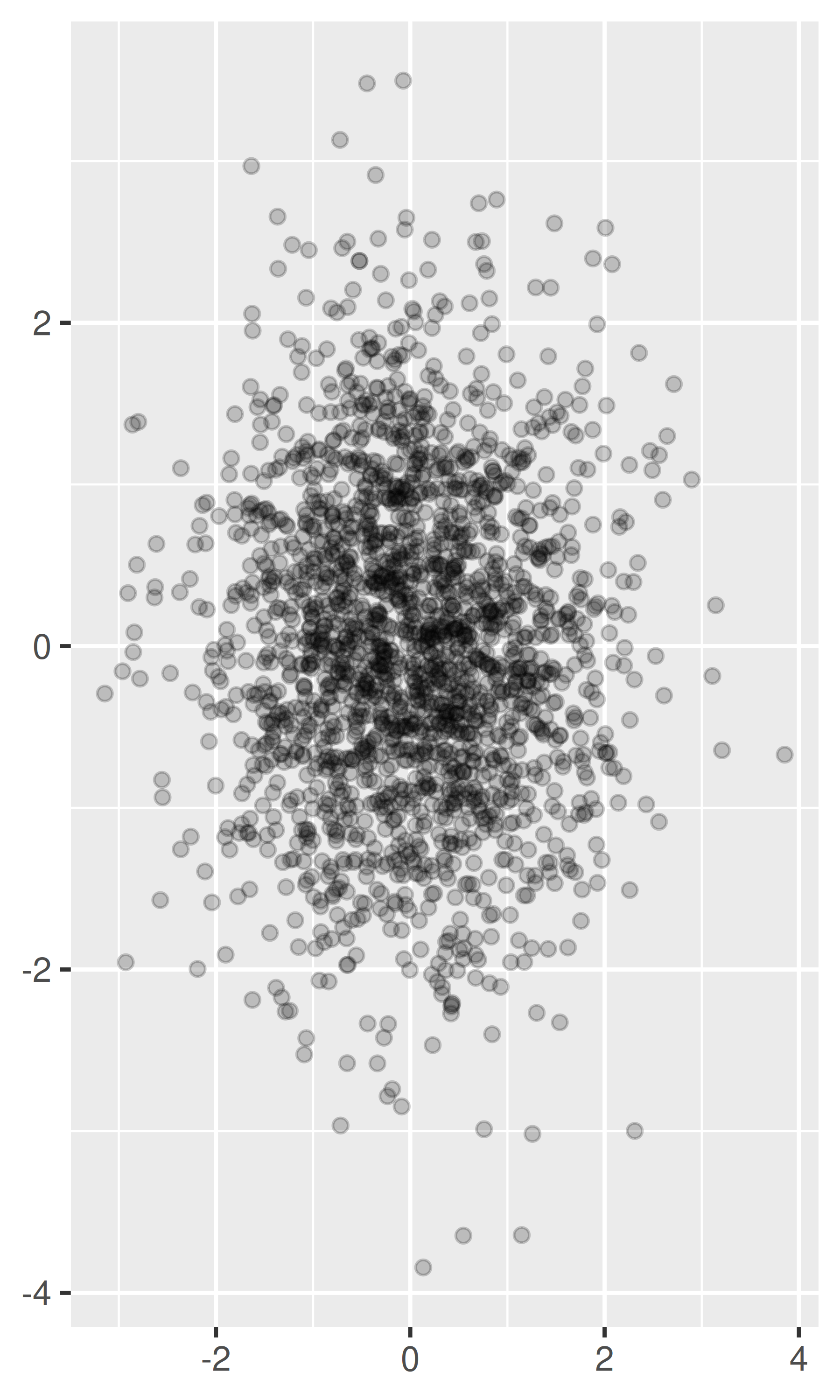
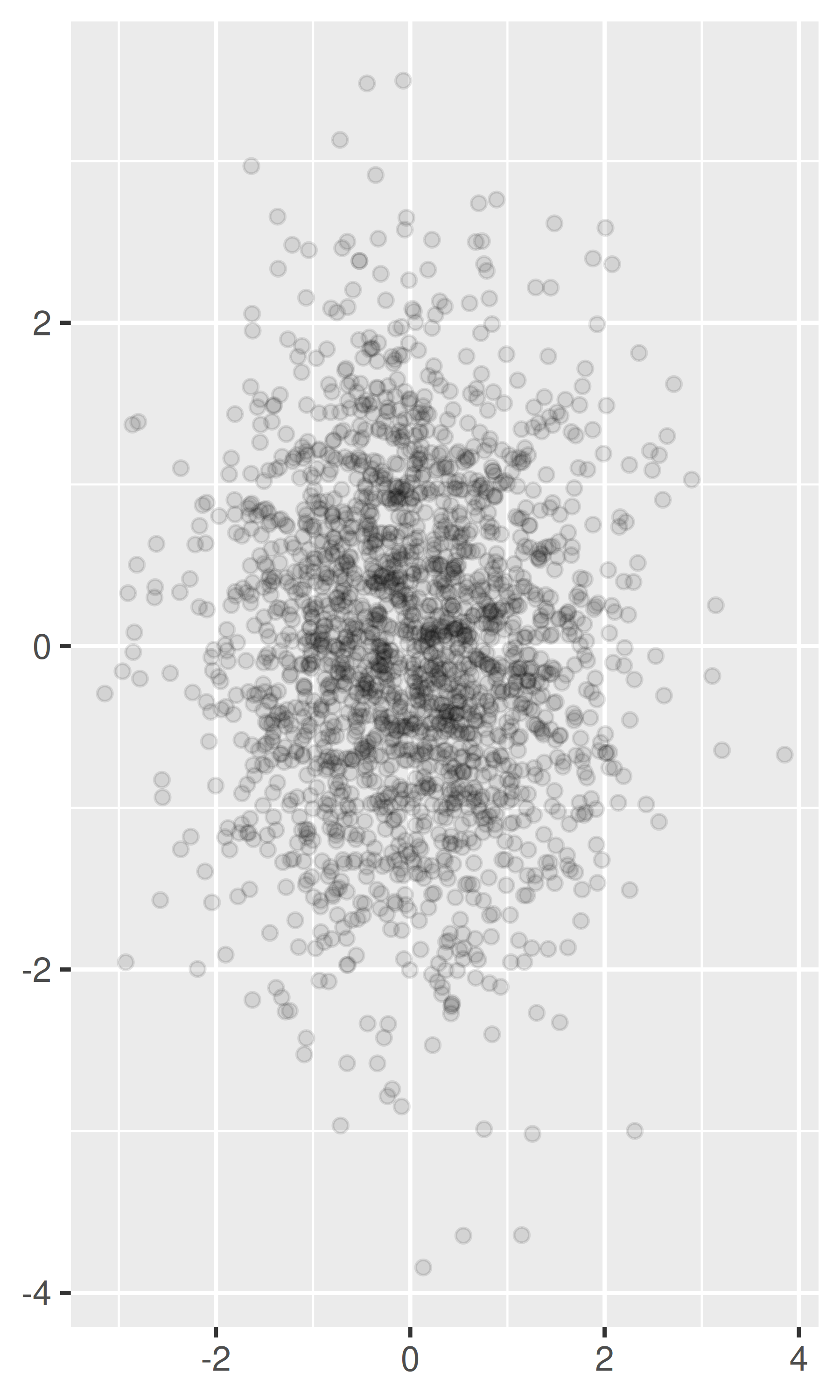
Si hay cierta discreción en los datos, puede alterar aleatoriamente los puntos para aliviar algunas superposiciones con
geom_jitter(). Esto puede resultar especialmente útil junto con la transparencia. De forma predeterminada, la cantidad de fluctuación agregada es el 40 % de la resolución de los datos, lo que deja un pequeño espacio entre las regiones adyacentes. Puede anular el valor predeterminado con los argumentoswidthyheight.
Alternativamente, podemos pensar en el sobregráfico como un problema de estimación de densidad 2D, lo que da lugar a dos enfoques más:
-
Agrupe los puntos y cuente el número en cada contenedor, luego visualice ese recuento (la segunda generalización del histograma),
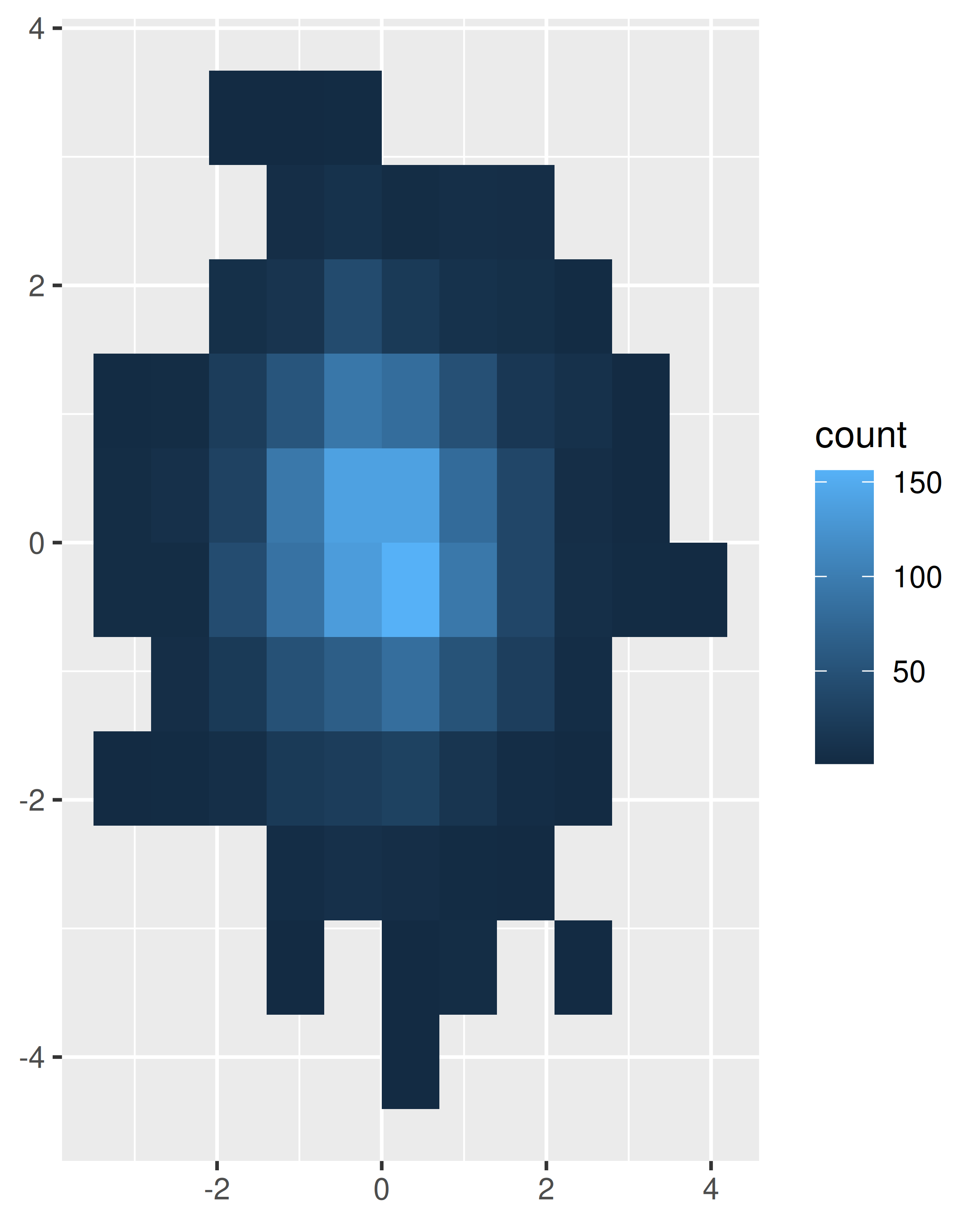
geom_bin2d(). Dividir la gráfica en muchos cuadrados pequeños puede producir artefactos visuales que distraigan. (D. B. Carr et al. 1987) sugiere usar hexágonos en su lugar, y esto se implementa engeom_hex(), usando el paquete hexbin (D. Carr, Lewin-Koh, y Mächler 2014).El siguiente código compara contenedores cuadrados y hexagonales, utilizando los parámetros
binsybinwidthpara controlar el número y el tamaño de los contenedores.norm + geom_bin2d() norm + geom_bin2d(bins = 10)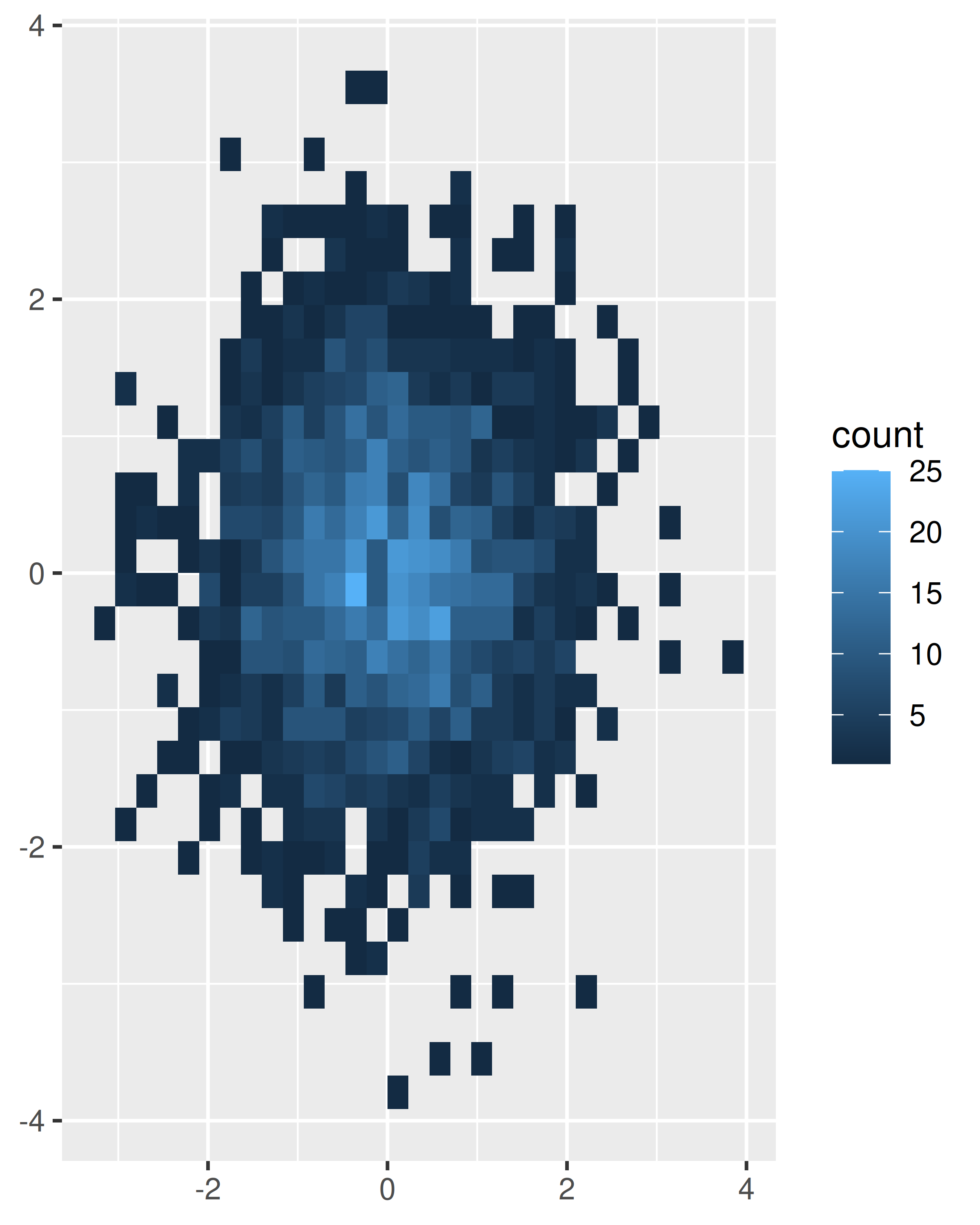
norm + geom_hex() norm + geom_hex(bins = 10)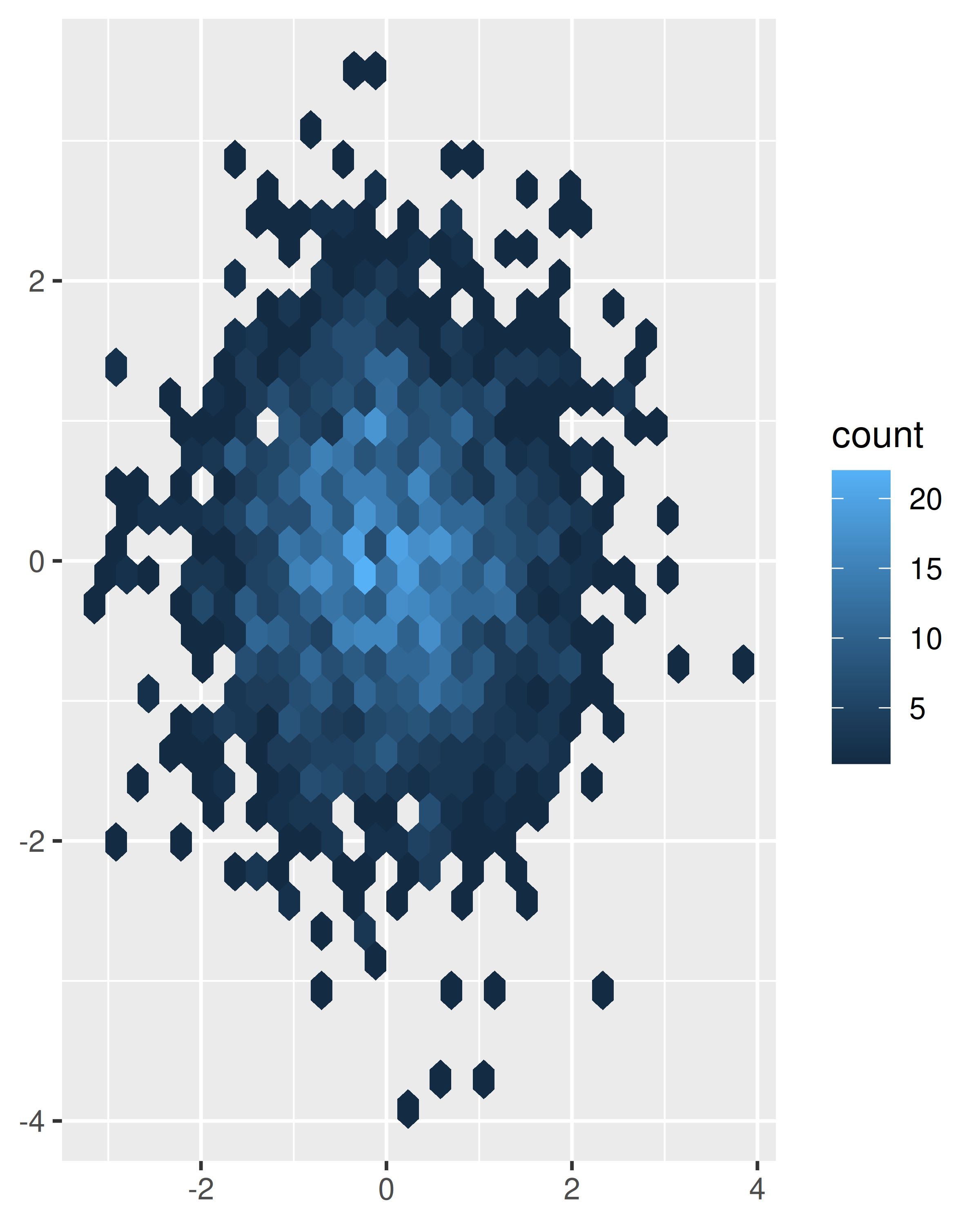
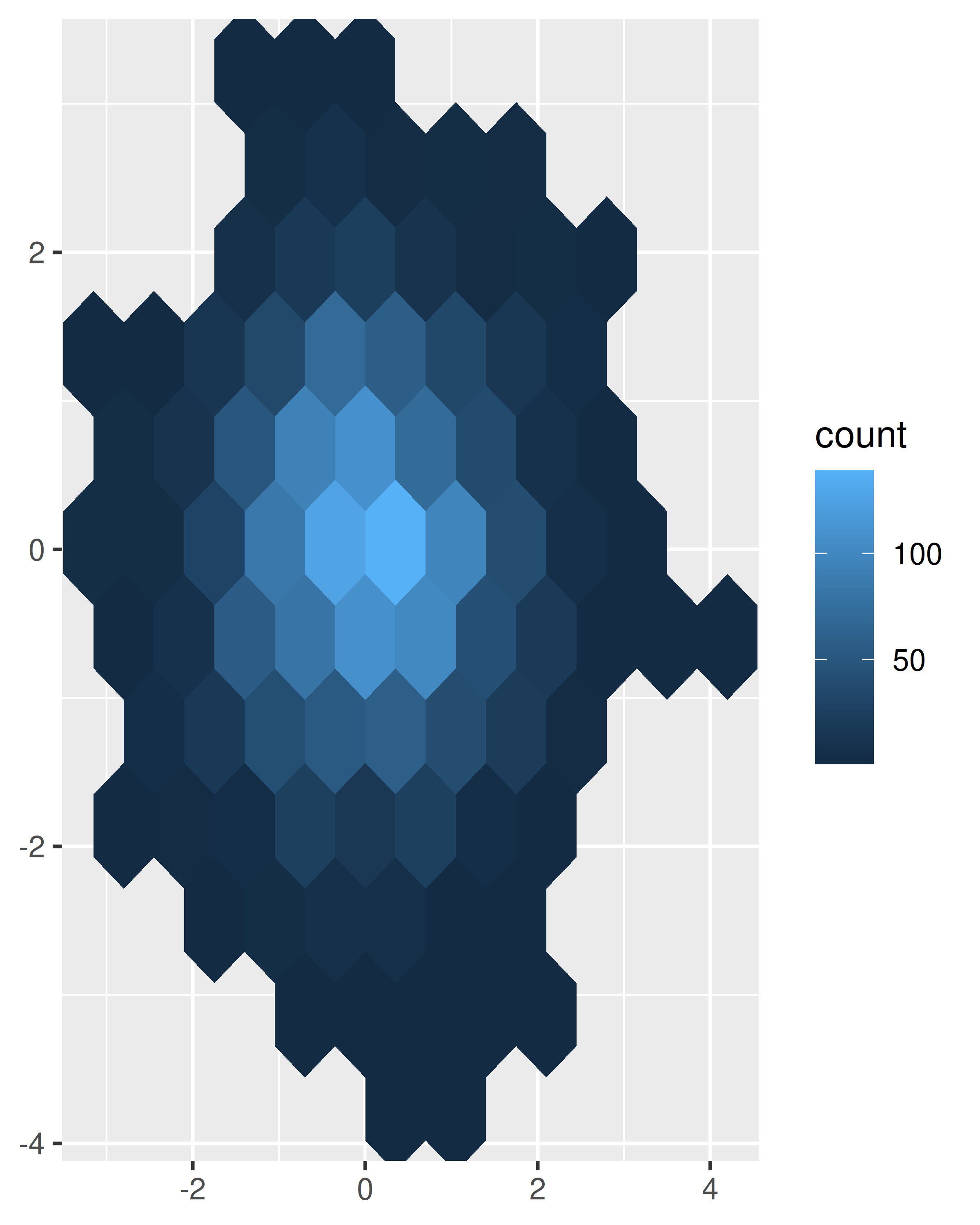
Estime la densidad 2d con
stat_density2d()y luego muéstrela usando una de las técnicas para mostrar superficies 3d en Sección 5.7.Si está interesado en la distribución condicional de y dado x, entonces las técnicas de Sección 2.6.3 también serán útil.
Otro enfoque para lidiar con el trazado excesivo es agregar resúmenes de datos para ayudar a guiar la vista hacia la verdadera forma del patrón dentro de los datos. Por ejemplo, podrías agregar una línea suave que muestre el centro de los datos con geom_smooth() o usar uno de los resúmenes siguientes.
5.6 Resúmenes estadísticos
geom_histogram() y geom_bin2d() usa una geom familiar, geom_bar() y geom_raster(), combinado con una nueva transformación estadística, stat_bin() y stat_bin2d(). stat_bin() y stat_bin2d() combine los datos en contenedores y cuente el número de observaciones en cada contenedor. Pero ¿y si queremos un resumen distinto al de contar? Hasta ahora, sólo hemos utilizado la transformación estadística predeterminada asociada con cada geom. Ahora vamos a explorar cómo usar stat_summary_bin() y stat_summary_2d() para calcular diferentes resúmenes.
Comencemos con un par de ejemplos con los datos de diamantes. El primer ejemplo de cada par muestra cómo podemos contar la cantidad de diamantes en cada contenedor; el segundo muestra cómo podemos calcular el precio promedio.
ggplot(diamonds, aes(color)) +
geom_bar()
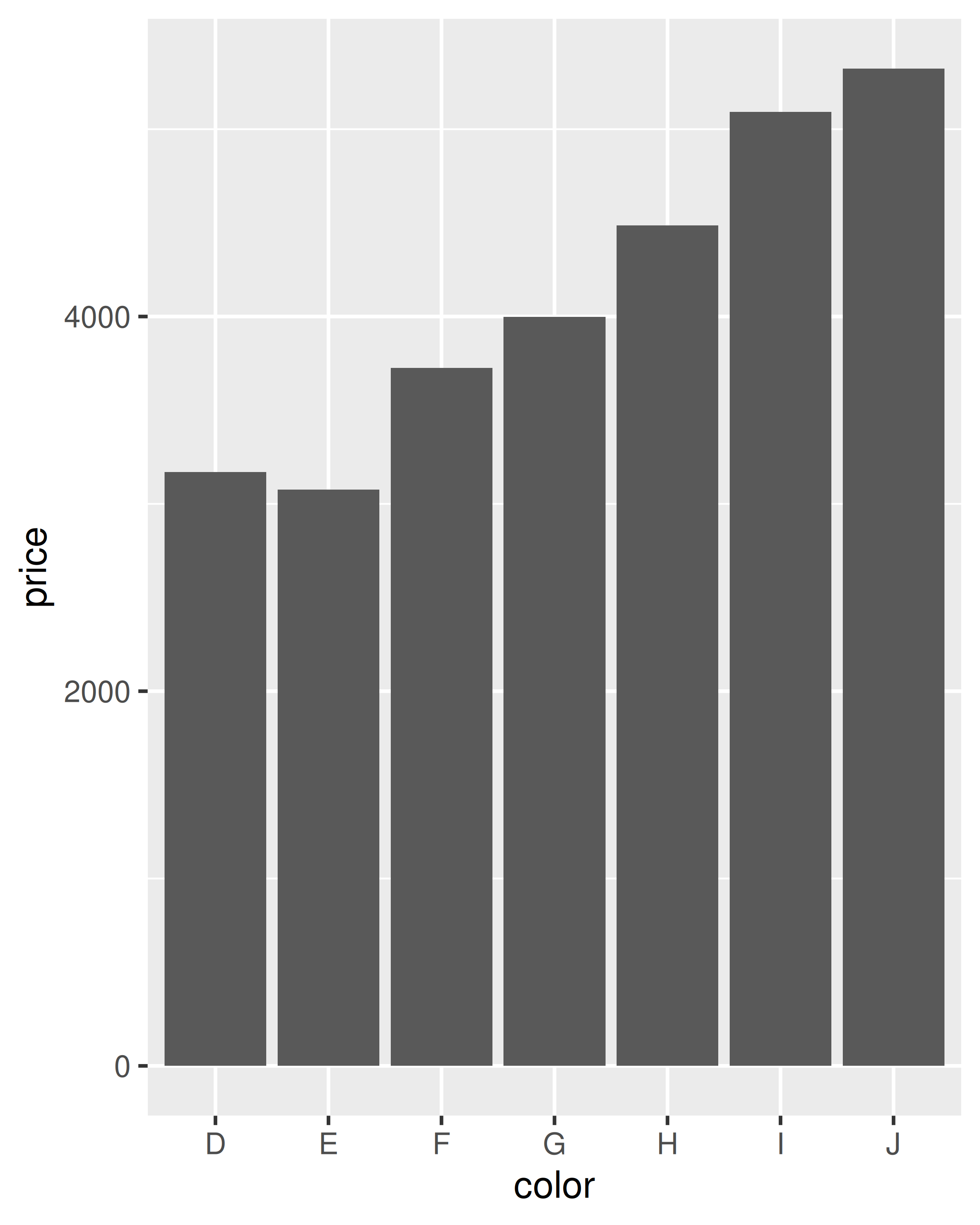
ggplot(diamonds, aes(color, price)) +
geom_bar(stat = "summary_bin", fun = mean)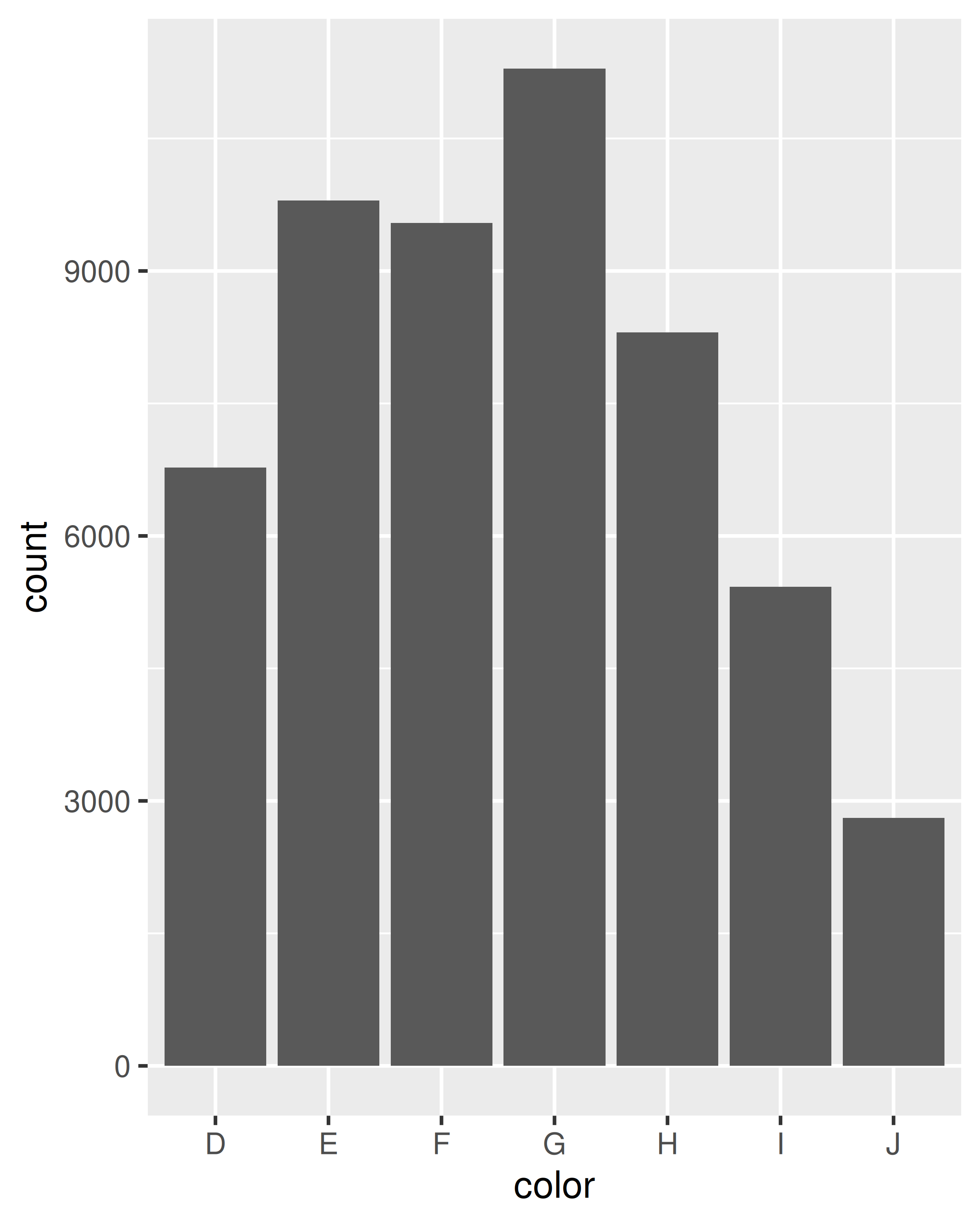
ggplot(diamonds, aes(table, depth)) +
geom_bin2d(binwidth = 1, na.rm = TRUE) +
xlim(50, 70) +
ylim(50, 70)
ggplot(diamonds, aes(table, depth, z = price)) +
geom_raster(binwidth = 1, stat = "summary_2d", fun = mean,
na.rm = TRUE) +
xlim(50, 70) +
ylim(50, 70)
#> Warning: Raster pixels are placed at uneven horizontal intervals and will be shifted
#> ℹ Consider using `geom_tile()` instead.
#> Raster pixels are placed at uneven horizontal intervals and will be shifted
#> ℹ Consider using `geom_tile()` instead.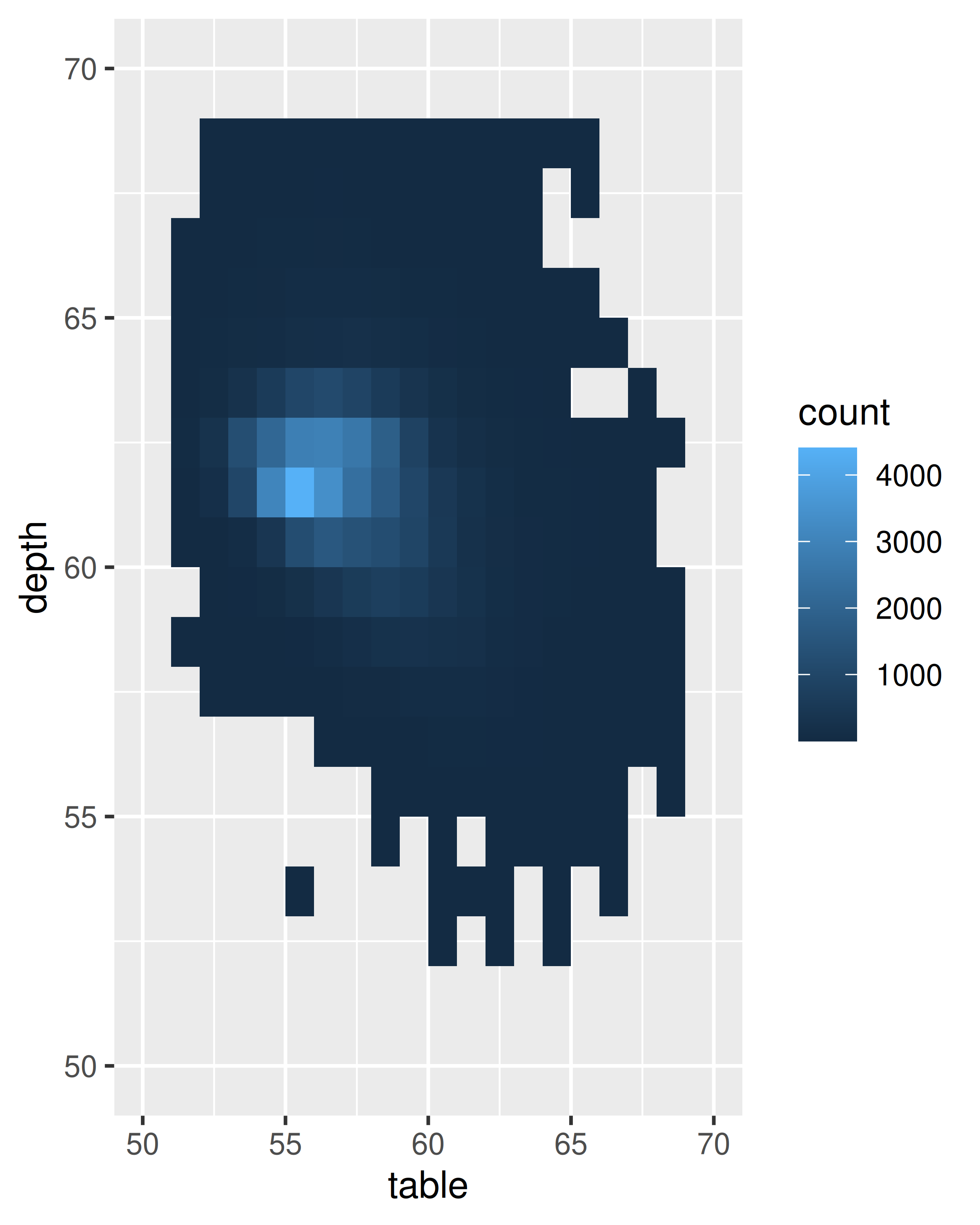
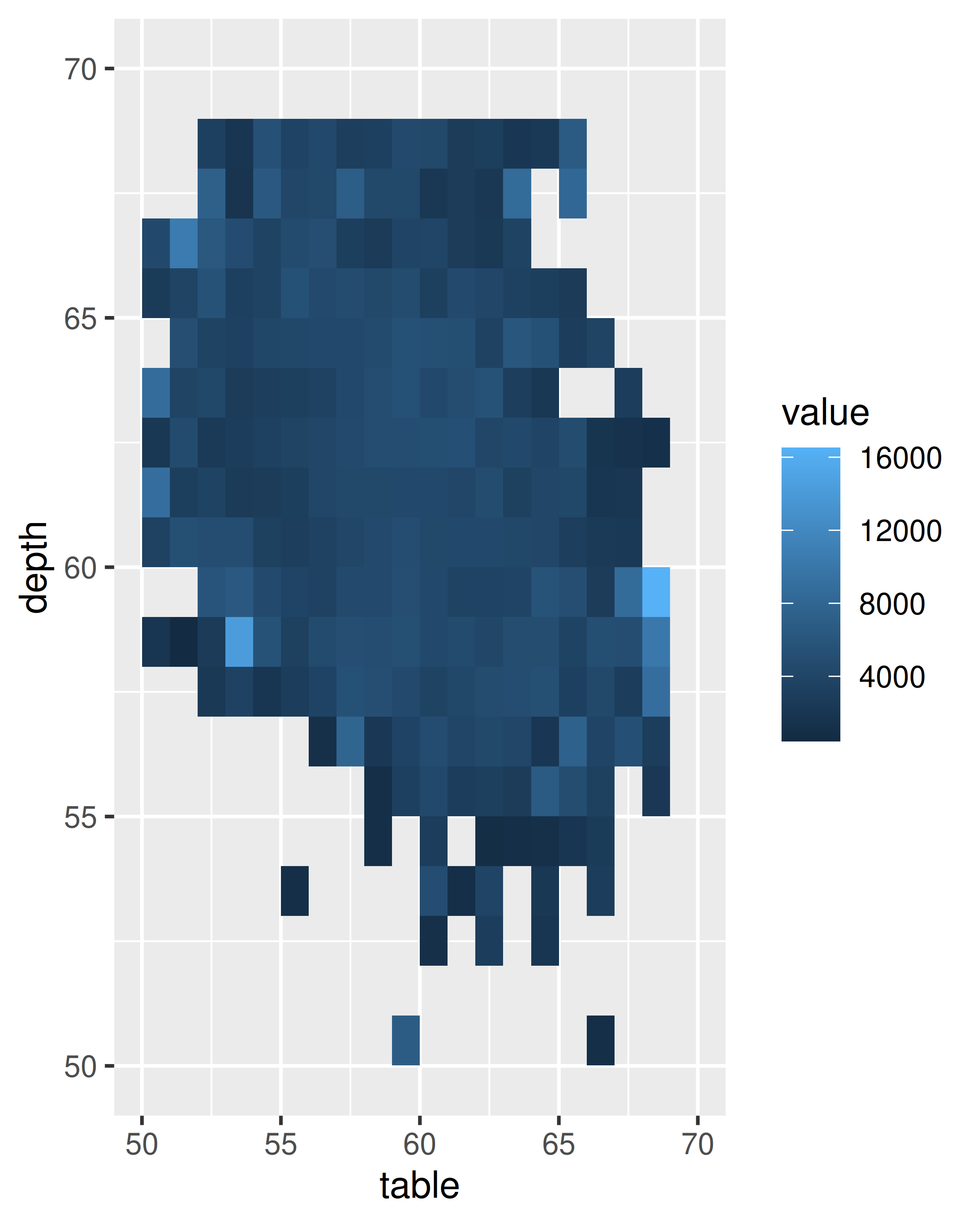
Para obtener más ayuda sobre los argumentos asociados con las dos transformaciones, consulte la ayuda para stat_summary_bin() y stat_summary_2d(). Puede controlar el tamaño de los contenedores y las funciones de resumen. stat_summary_bin() puede producir y, ymin y ymax estética, lo que también lo hace útil para mostrar medidas de propagación. Consulte los documentos para obtener más detalles. Aprenderás más sobre cómo interactúan las geoms y las estadísticas en Sección 13.6.
Estas funciones de resumen son bastante limitadas, pero suelen ser útiles para dar un primer vistazo rápido a un problema. Si los encuentra restrictivos, deberá hacer los resúmenes usted mismo (consulte R para la Ciencia de Datos https://r4ds.had.co.nz para más detalles)
5.7 Superficies
Hasta ahora hemos considerado dos clases de geoms:
Geomas simples donde hay una correspondencia uno a uno entre las filas en el marco de datos y los elementos físicos de la geom.
Geomas estadísticas donde se introduce una capa de resúmenes estadísticos entre los datos sin procesar y el resultado.
Ahora consideraremos casos en los que se requiere una visualización de una superficie tridimensional. El paquete ggplot2 no admite superficies 3D reales, pero sí admite muchas herramientas comunes para resumir superficies 3D en 2D: contornos, mosaicos de colores y diagramas de burbujas. Todos funcionan de manera similar, diferenciándose sólo en la estética utilizada para la tercera dimensión. A continuación se muestra un ejemplo de un gráfico de contorno:
ggplot(faithfuld, aes(eruptions, waiting)) +
geom_contour(aes(z = density, colour = ..level..))
#> Warning: The dot-dot notation (`..level..`) was deprecated in ggplot2 3.4.0.
#> ℹ Please use `after_stat(level)` instead.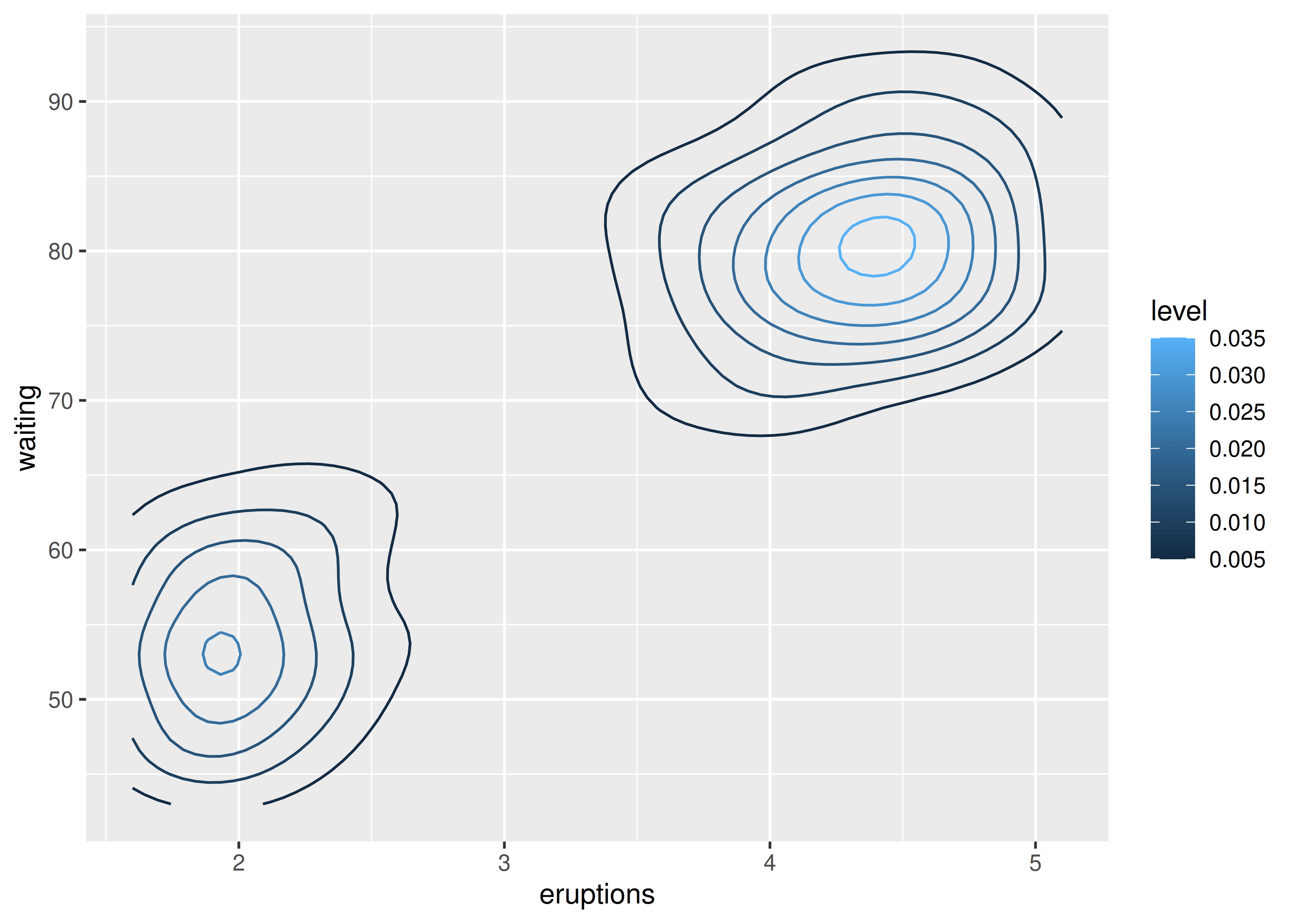
La referencia a la variable ..level... en este código puede parecer confusa, porque no hay ninguna variable llamada ...level... en los datos de faithfuld. En este contexto, la notación .. se refiere a una variable calculada internamente (consulte Sección 13.6.1). Para mostrar la misma densidad que un mapa de calor, puede utilizar geom_raster():
ggplot(faithfuld, aes(eruptions, waiting)) +
geom_raster(aes(fill = density))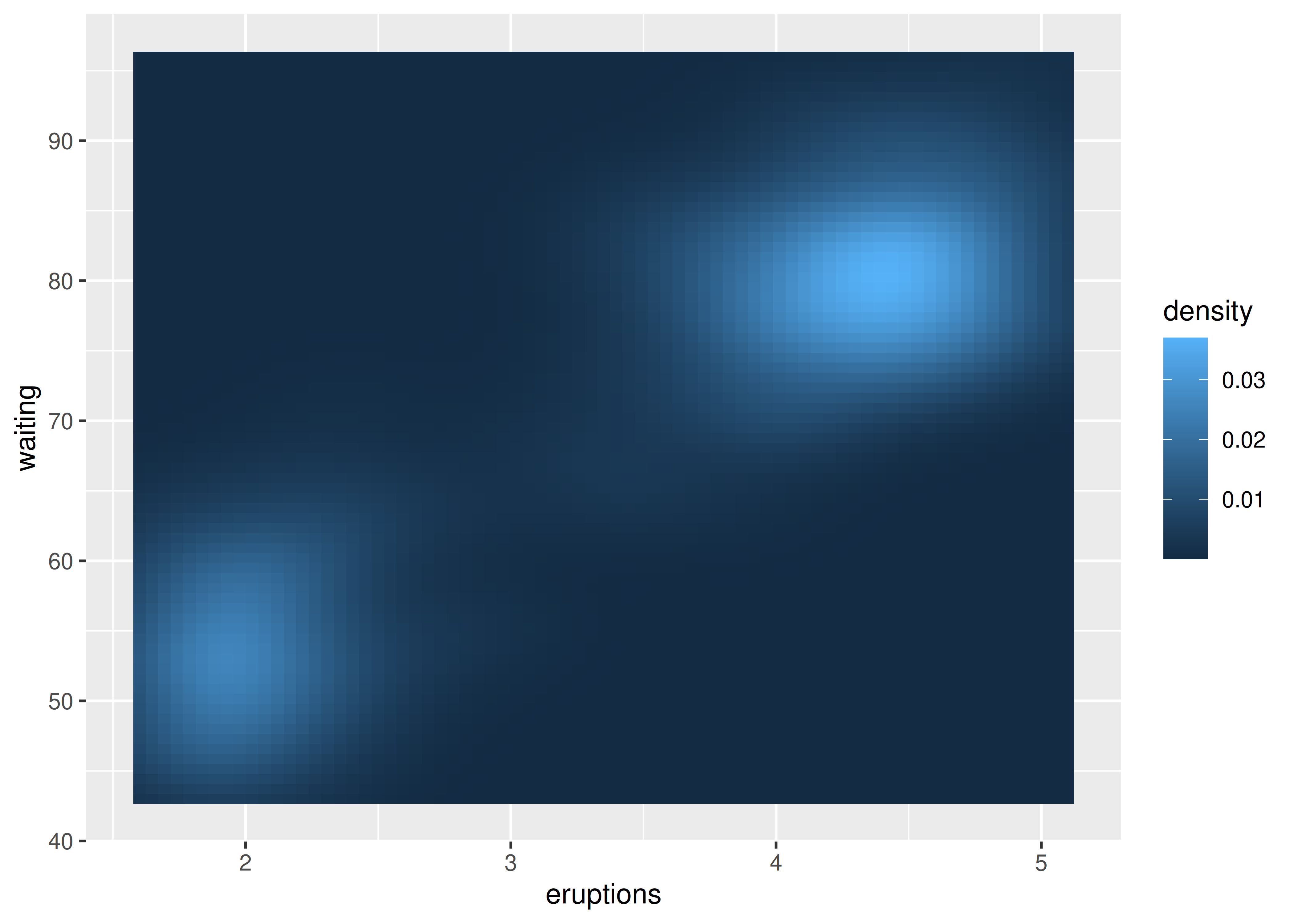
# Los gráficos de burbujas funcionan mejor con menos observaciones
small <- faithfuld[seq(1, nrow(faithfuld), by = 10), ]
ggplot(small, aes(eruptions, waiting)) +
geom_point(aes(size = density), alpha = 1/3) +
scale_size_area()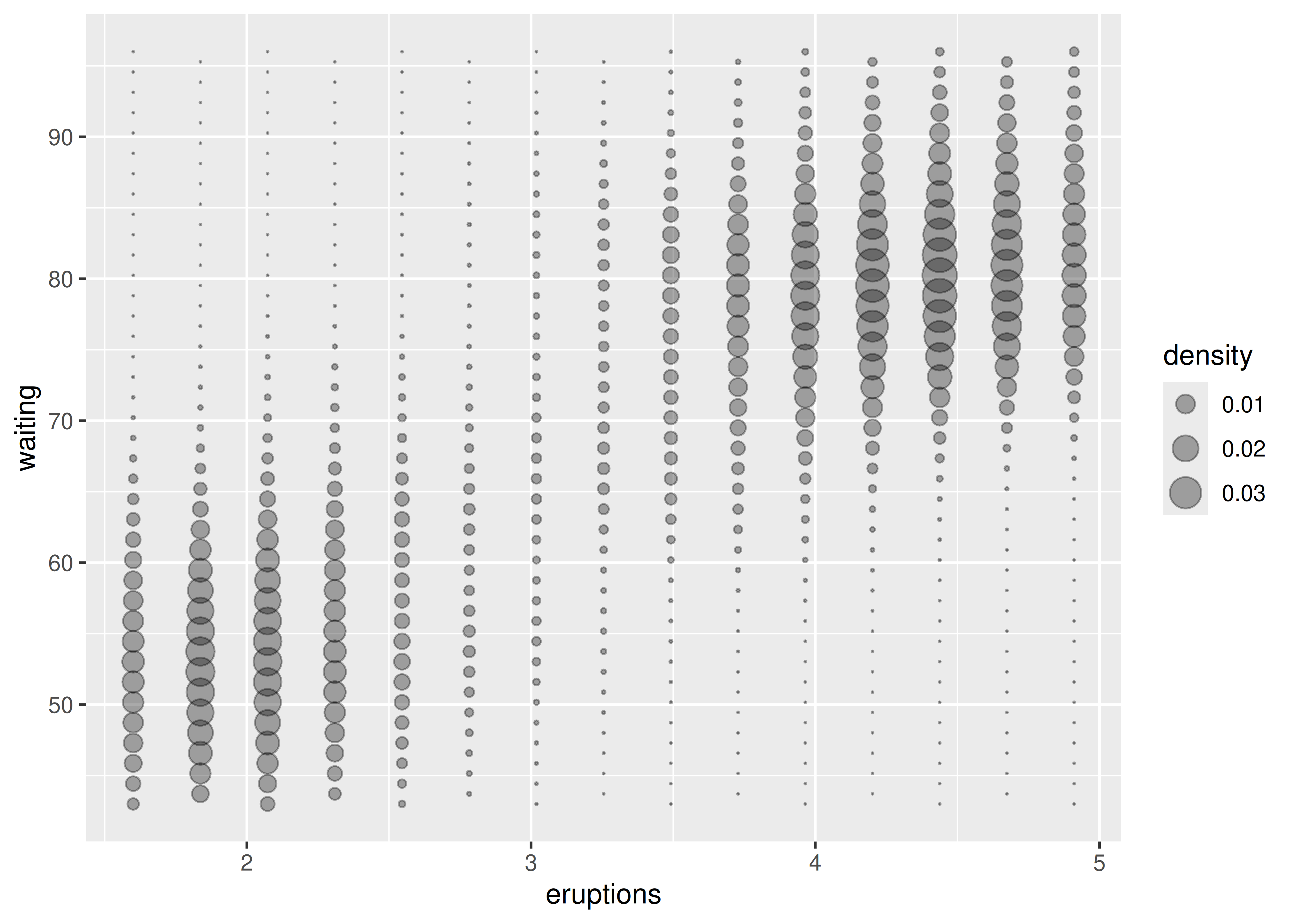
Para gráficos 3D interactivos, incluidas superficies 3D reales, consulte RGL, http://rgl.neoscientists.org/about.shtml.