2 Primeros pasos

You are reading the work-in-progress third edition of the ggplot2 book. This chapter is currently a dumping ground for ideas, and we don’t recommend reading it.

2.1 Introducción

El objetivo de este capítulo es enseñarle cómo producir gráficos útiles con ggplot2 lo más rápido posible. Aprenderá los conceptos básicos de ggplot() junto con algunas “recetas” útiles para crear los gráficos más importantes. ggplot() te permite crear gráficos complejos con sólo unas pocas líneas de código porque se basa en una rica teoría subyacente, la gramática de los gráficos. Aquí nos saltaremos la teoría y nos centraremos en la práctica, y en capítulos posteriores aprenderá a utilizar todo el poder expresivo de la gramática.

En este capítulo aprenderás:

Acerca del conjunto de datos mpg incluido con ggplot2, Sección 2.2.
Los tres componentes clave de cada gráfica: datos, estética y geoms, Sección 2.3.
Cómo agregar variables adicionales a una gráfica con estética, Sección 2.4.
Cómo mostrar variables categóricas adicionales en un gráfico utilizando pequeños múltiplos creados mediante facetado, Sección 2.5.
Una variedad de geoms diferentes que puedes usar para crear diferentes tipos de gráficos, Sección 2.6.
Cómo modificar los ejes, Sección 2.7.
Cosas que puedes hacer con un objeto de trazado además de mostrarlo, como guardarlo en el disco, Sección 2.8.

2.2 Datos de economía de combustible

En este capítulo, usaremos principalmente un conjunto de datos incluido con ggplot2: mpg. Incluye información sobre la economía de combustible de modelos de automóviles populares en 1999 y 2008, recopilada por la Agencia de Protección Ambiental de EE. UU., http://fueleconomy.gov. Puede acceder a los datos cargando ggplot2:

library(ggplot2)
mpg
#> # A tibble: 234 × 11
#>   manufacturer model displ  year   cyl trans      drv     cty   hwy fl    class 
#>   <chr>        <chr> <dbl> <int> <int> <chr>      <chr> <int> <int> <chr> <chr> 
#> 1 audi         a4      1.8  1999     4 auto(l5)   f        18    29 p     compa…
#> 2 audi         a4      1.8  1999     4 manual(m5) f        21    29 p     compa…
#> 3 audi         a4      2    2008     4 manual(m6) f        20    31 p     compa…
#> 4 audi         a4      2    2008     4 auto(av)   f        21    30 p     compa…
#> 5 audi         a4      2.8  1999     6 auto(l5)   f        16    26 p     compa…
#> 6 audi         a4      2.8  1999     6 manual(m5) f        18    26 p     compa…
#> # ℹ 228 more rows

La mayoría de las variables se explican por sí solas:

cty y hwy registran millas por galón (mpg) para conducción en ciudad y carretera.
displ es la cilindrada del motor en litros.
drv es la transmisión: rueda delantera (f), rueda trasera (r) o cuatro ruedas (4).
model es el modelo de coche. Son 38 modelos, seleccionados porque tuvieron una nueva edición cada año entre 1999 y 2008.
class es una variable categórica que describe el “tipo” de coche: biplaza, SUV, compacto, etc.

Este conjunto de datos sugiere muchas preguntas interesantes. ¿Cómo se relacionan el tamaño del motor y la economía de combustible? ¿Algunos fabricantes se preocupan más por el ahorro de combustible que otros? ¿Ha mejorado la economía de combustible en los últimos diez años? Intentaremos responder algunas de estas preguntas y, en el proceso, aprenderemos cómo crear algunos gráficos básicos con ggplot2.

2.2.1 Ejercicios

Enumere cinco funciones que podría utilizar para obtener más información sobre el conjunto de datos mpg.
¿Cómo puede saber qué otros conjuntos de datos se incluyen con ggplot2?
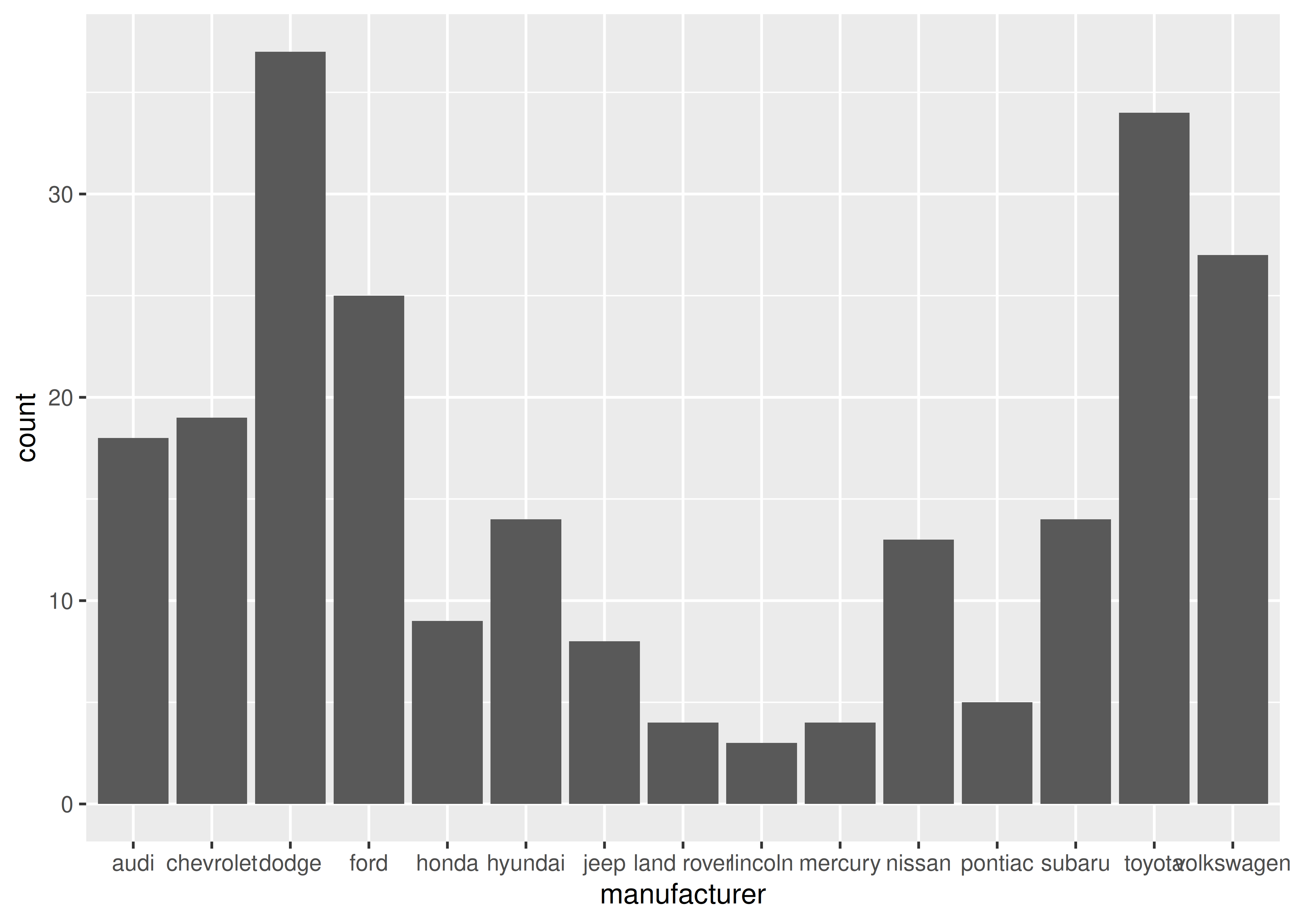
Aparte de EE. UU., la mayoría de los países utilizan el consumo de combustible (combustible consumido en una distancia fija) en lugar de la economía de combustible (distancia recorrida con una cantidad fija de combustible). ¿Cómo se podrían convertir cty y hwy al estándar europeo de l/100 km?
¿Qué fabricante tiene más modelos en este conjunto de datos? ¿Qué modelo tiene más variaciones? ¿Cambia su respuesta si elimina la especificación redundante del tren motriz (por ejemplo, “pathfinder 4wd”, “a4 quattro”) del nombre del modelo?

2.3 Componentes clave

Cada gráfico de ggplot2 tiene tres componentes clave:

datos,
Un conjunto de mapeos estéticos entre variables en los datos y propiedades visuales, y
Al menos una capa que describa cómo representar cada observación. Las capas generalmente se crean con una función geom.

He aquí un ejemplo sencillo:

ggplot(mpg, aes(x = displ, y = hwy)) + 
  geom_point()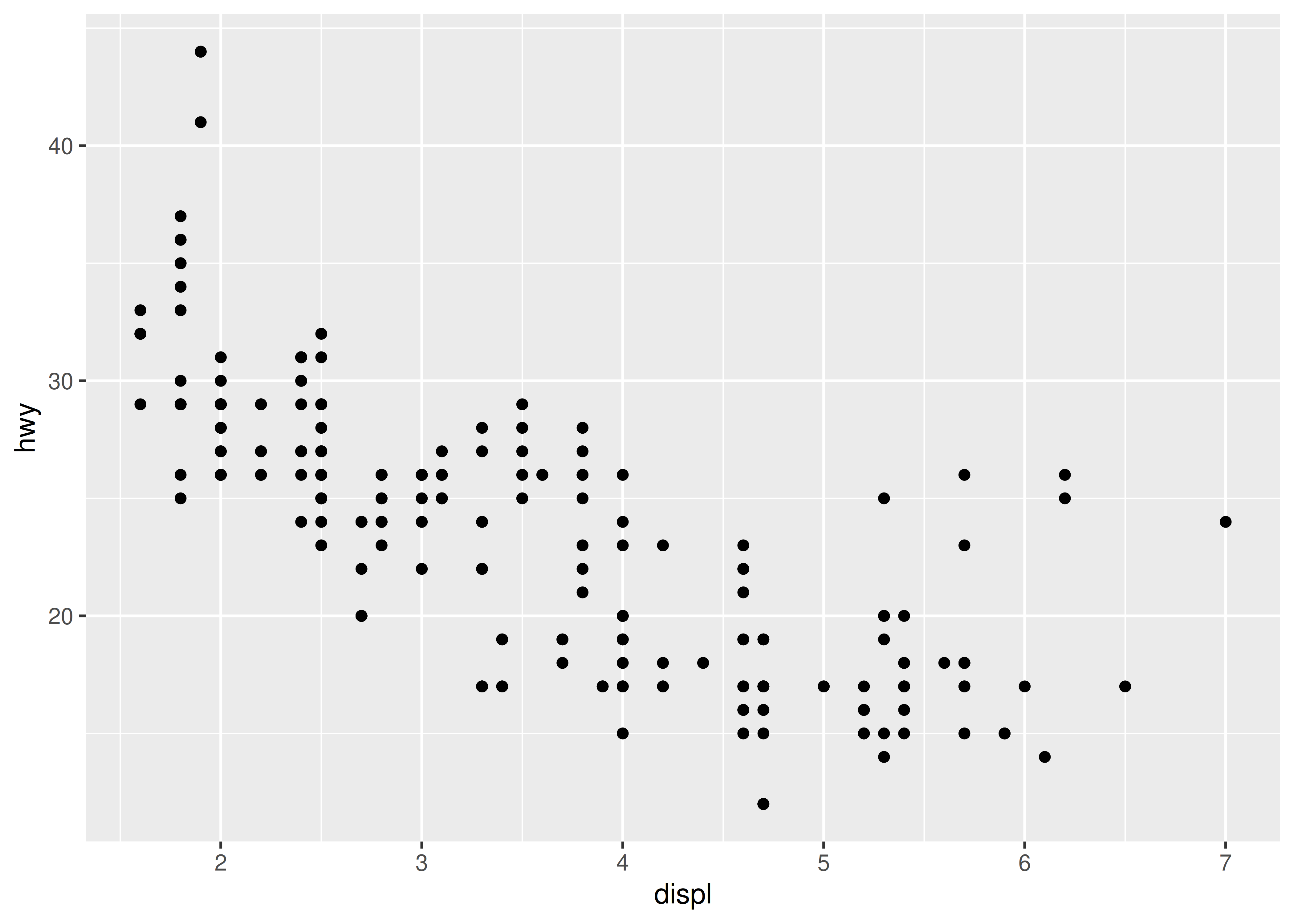

Esto produce un diagrama de dispersión definido por:

Datos: mpg.
Mapeo estético: tamaño del motor asignado a la posición x, economía de combustible a la posición y.
Capa: puntos.

Preste atención a la estructura de esta llamada a función: los datos y las asignaciones estéticas se proporcionan en ggplot(), luego las capas se agregan con +. Este es un patrón importante y, a medida que aprenda más sobre ggplot2, construirá gráficos cada vez más sofisticados agregando más tipos de componentes.

Casi todos los gráficos asignan una variable a x e y, por lo que nombrar estas estéticas es tedioso, por lo que los dos primeros argumentos sin nombre de aes() se asignarán a x e y. Esto significa que el siguiente código es idéntico al ejemplo anterior:

ggplot(mpg, aes(displ, hwy)) +
  geom_point()

Nos apegaremos a ese estilo a lo largo del libro, así que no olvide que los dos primeros argumentos de aes() son x e y. Tenga en cuenta que hemos puesto cada comando en una nueva línea. Recomendamos hacer esto en su propio código, para que sea fácil escanear una especificación de trazado y ver exactamente lo que hay allí. En este capítulo, a veces usaremos solo una línea por gráfico, porque hace que sea más fácil ver las diferencias entre las variaciones del argumento.

El gráfico muestra una fuerte correlación: a medida que aumenta el tamaño del motor, empeora la economía de combustible. También hay algunos valores atípicos interesantes: algunos automóviles con motores grandes obtienen una economía de combustible mayor que el promedio. ¿Qué tipo de coches crees que son?

2.3.1 Ejercicios

¿Cómo describirías la relación entre cty y hwy? ¿Tiene alguna inquietud acerca de sacar conclusiones de esa gráfica?
¿Qué muestra ggplot(mpg, aes(modelo, fabricante)) + geom_point()? ¿Es útil? ¿Cómo podrías modificar los datos para hacerlos más informativos?
Describe los datos, los mapeos estéticos y las capas utilizadas para cada uno de los siguientes gráficos. Tendrás que adivinar un poco porque aún no has visto todos los conjuntos de datos y funciones, ¡pero usa tu sentido común! Vea si puede predecir cómo se verá la gráfica antes de ejecutar el código.
1. ggplot(mpg, aes(cty, hwy)) + geom_point()
2. ggplot(diamonds, aes(carat, price)) + geom_point()
3. ggplot(economics, aes(date, unemploy)) + geom_line()
4. ggplot(mpg, aes(cty)) + geom_histogram()

2.4 Color, tamaño, forma y otros atributos estéticos

Para agregar variables adicionales a una gráfica, podemos usar otras estéticas como color, forma y tamaño (NB: si bien usamos la ortografía británica en este libro, ggplot2 también acepta la ortografía estadounidense). Estos funcionan de la misma manera que la estética x e y, y se agregan a la llamada a aes():

aes(displ, hwy, colour = class)
aes(displ, hwy, shape = drv)
aes(displ, hwy, size = cyl)

ggplot2 se encarga de los detalles de convertir datos (p. ej., ‘f’, ‘r’, ‘4’) en estética (p. ej., ‘rojo’, ‘amarillo’, ‘verde’) con una escala. Hay una escala para cada mapeo estético en una gráfica. La escala también se encarga de crear una guía, un eje o leyenda, que permite leer el trazado, convirtiendo nuevamente los valores estéticos en valores de datos. Por ahora, nos quedaremos con las escalas predeterminadas proporcionadas por ggplot2. Aprenderá cómo anularlos en ?sec-scale-color.

Para aprender más sobre esas variables atípicas en el diagrama de dispersión anterior, podríamos asignar la variable de clase al color:

ggplot(mpg, aes(displ, hwy, colour = class)) + 
  geom_point()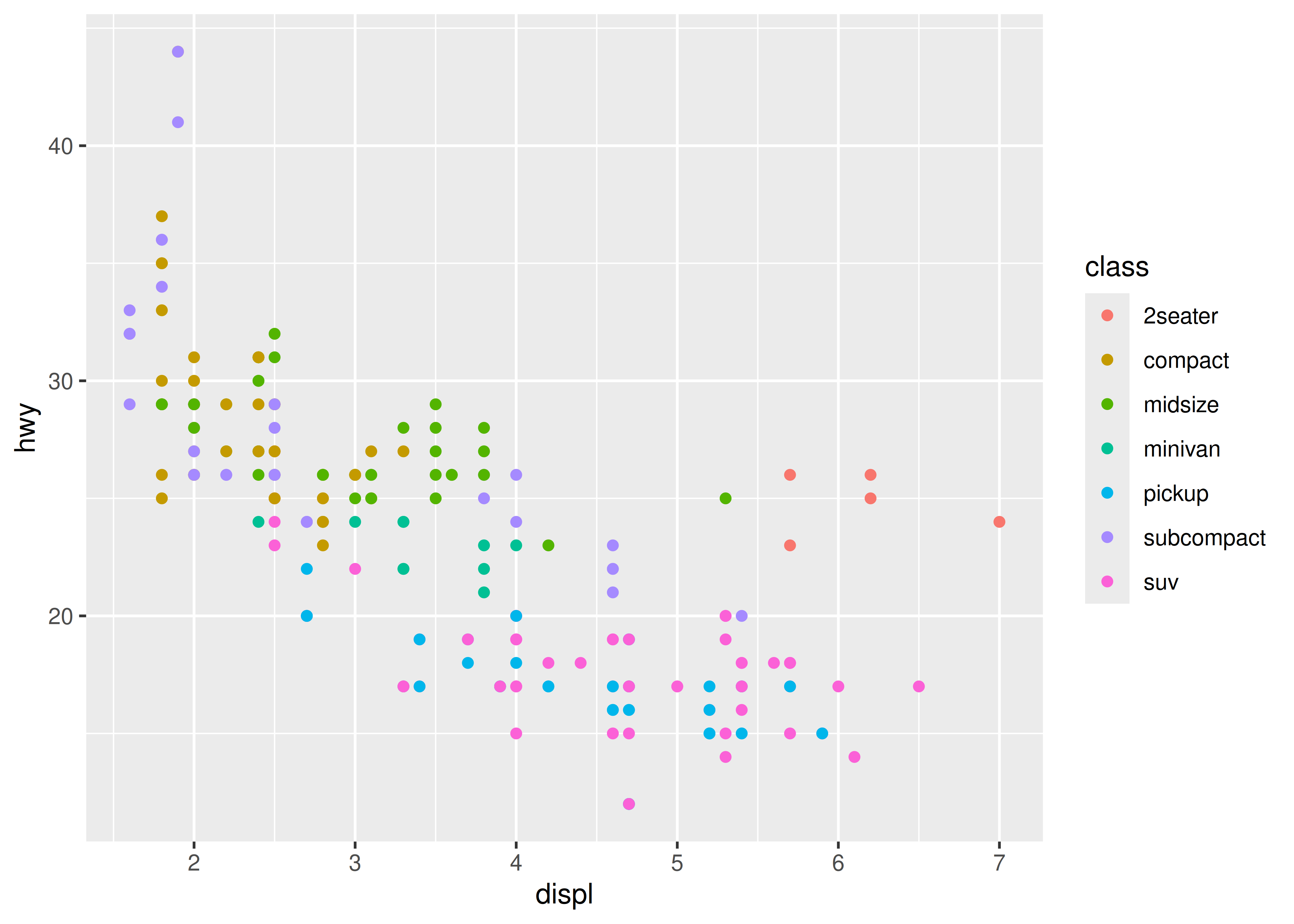

Esto le da a cada punto un color único correspondiente a su clase. La leyenda nos permite leer los valores de los datos del color, mostrándonos que el grupo de coches con un consumo de combustible inusualmente alto para su tamaño de motor son los biplaza: coches con motores grandes, pero carrocerías ligeras.

Si desea establecer una estética en un valor fijo, sin escalarla, hágalo en la capa individual fuera de aes(). Compare los dos gráficos siguientes:

ggplot(mpg, aes(displ, hwy)) + geom_point(aes(colour = "blue"))
ggplot(mpg, aes(displ, hwy)) + geom_point(colour = "blue")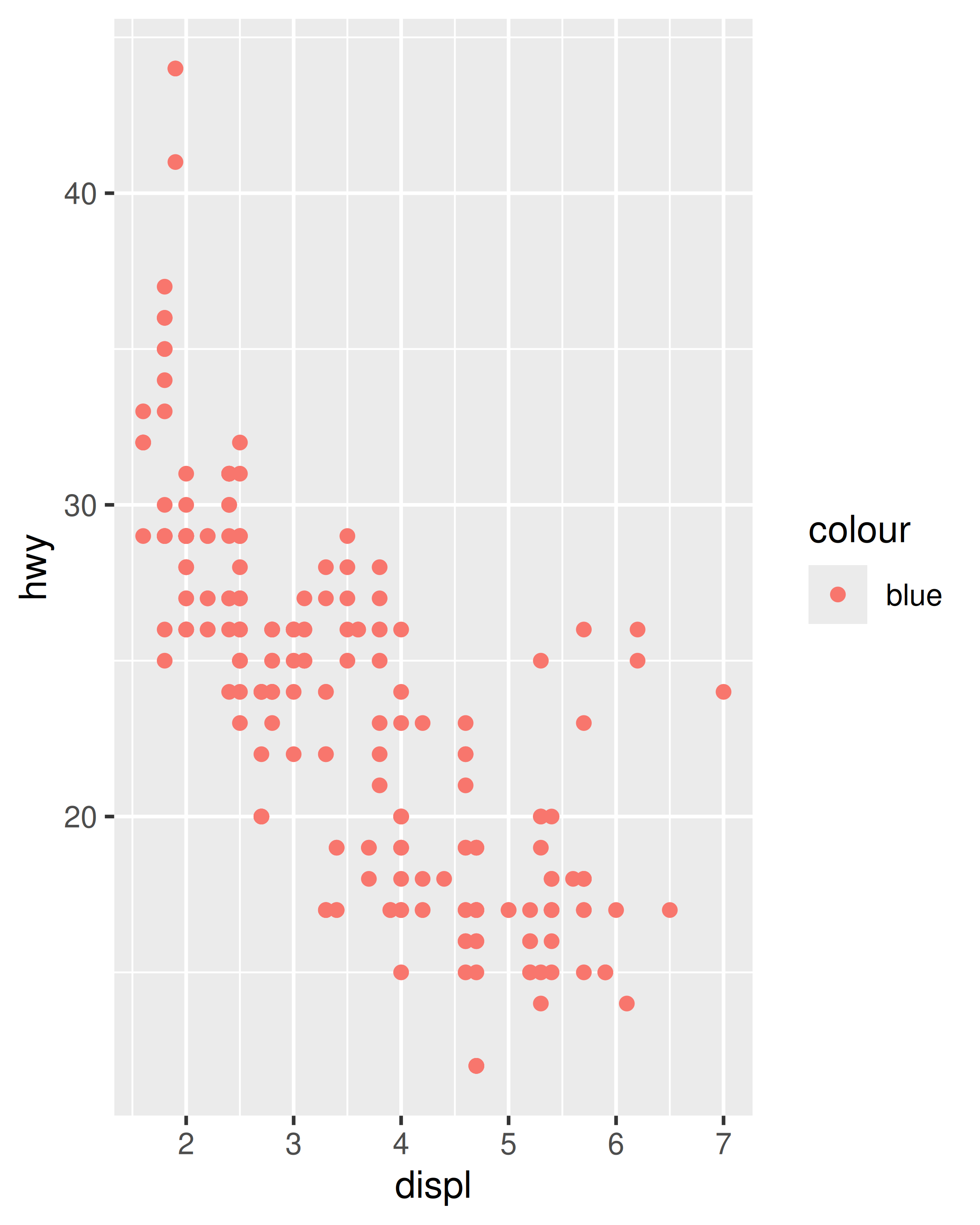

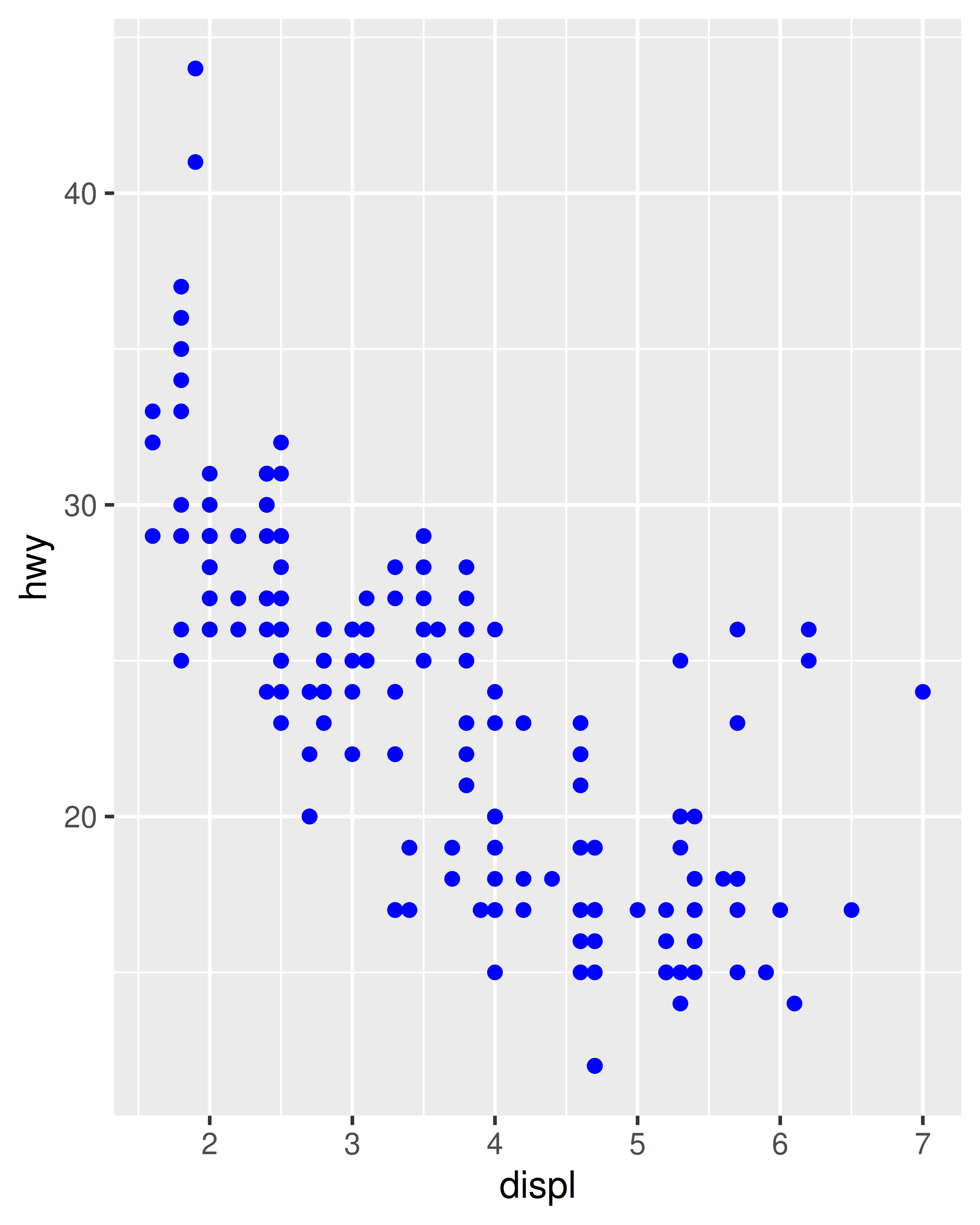
En el primer gráfico, el valor “azul” se escala a un color rosado y se agrega una leyenda. En el segundo gráfico, a los puntos se les da el color R azul. Esta es una técnica importante y aprenderá más sobre ella en Sección 13.4.2. Consulte vignette("ggplot2-specs") para conocer los valores necesarios para el color y otras estéticas.

Diferentes tipos de atributos estéticos funcionan mejor con diferentes tipos de variables. Por ejemplo, el color y la forma funcionan bien con variables categóricas, mientras que el tamaño funciona bien con variables continuas. La cantidad de datos también marca la diferencia: si hay muchos datos, puede resultar difícil distinguir diferentes grupos. Una solución alternativa es utilizar facetado, como se describe a continuación.

Cuando se utiliza la estética en una gráfica, menos suele ser más. Es difícil ver las relaciones simultáneas entre el color, la forma y el tamaño, por lo que hay que ser moderado al utilizar la estética. En lugar de intentar crear una gráfica muy compleja que muestre todo a la vez, intenta crear una serie de gráficas simples que cuenten una historia y lleven al lector de la ignorancia al conocimiento.

2.4.1 Ejercicios

Experimente con la estética del color, la forma y el tamaño. ¿Qué sucede cuando los asignas a valores continuos? ¿Qué pasa con los valores categóricos? ¿Qué sucede cuando usas más de una estética en una gráfica?
¿Qué sucede si asignas una variable continua a una forma? ¿Por qué? ¿Qué sucede si asignas trans a la forma? ¿Por qué?
¿Cómo se relaciona el tren motriz con la economía de combustible? ¿Cómo se relaciona el tren motriz con el tamaño y la clase del motor?

2.5 Facetado

Otra técnica para mostrar variables categóricas adicionales en un gráfico es el facetado. Facetado crea tablas de gráficos dividiendo los datos en subconjuntos y mostrando el mismo gráfico para cada subconjunto. Aprenderá más sobre facetado en Capítulo 16, pero es una técnica tan útil que necesita conocerla de inmediato.

Hay dos tipos de facetado: rejilla y envuelto. Envuelto es el más útil, por lo que lo discutiremos aquí y podrá aprender sobre el facetado de cuadrícula más adelante. Para facetar un gráfico simplemente agrega una especificación de facetado con facet_wrap(), que toma el nombre de una variable precedida por ~.

ggplot(mpg, aes(displ, hwy)) + 
  geom_point() + 
  facet_wrap(~class)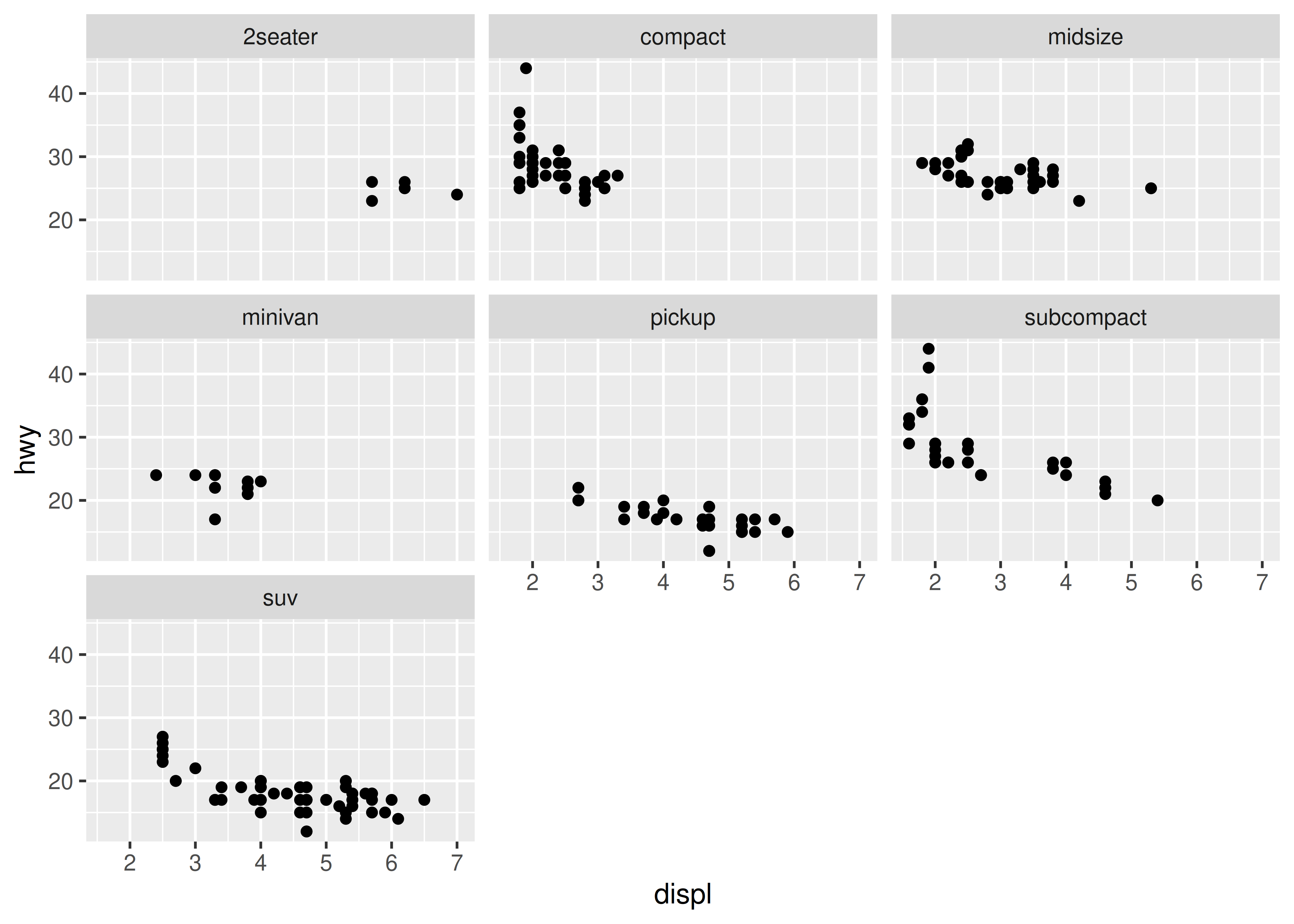

Quizás se pregunte cuándo utilizar facetado y cuándo utilizar estética. Aprenderá más sobre las ventajas y desventajas relativas de cada uno en Sección 16.5.

2.5.1 Ejercicios

¿Qué sucede si intentas facetar con una variable continua como hwy? ¿Qué pasa con cyl? ¿Cuál es la diferencia clave?
Utilice facetado para explorar la relación triple entre economía de combustible, tamaño del motor y cantidad de cilindros. ¿Cómo cambia el facetado por número de cilindros su evaluación de la relación entre el tamaño del motor y la economía de combustible?
Lea la documentación de facet_wrap(). ¿Qué argumentos puedes usar para controlar cuántas filas y columnas aparecen en el resultado?
¿Qué hace el argumento scales de facet_wrap()? ¿Cuándo podrías usarlo?

2.6 Trazar geomas

Podrías adivinar que al sustituir geom_point() por una función geom diferente, obtendrías un tipo diferente de gráfico. ¡Es una gran suposición! En las siguientes secciones, aprenderá sobre algunas de las otras geoms importantes proporcionadas en ggplot2. Esta no es una lista exhaustiva, pero debería cubrir los tipos de gráfica más utilizados. Aprenderá más en Capítulo 3 y Capítulo 4.

geom_smooth() ajusta un suavizador a los datos y muestra el suavizado y su error estándar.
geom_boxplot() produce un diagrama de caja y bigotes para resumir la distribución de un conjunto de puntos.
geom_histogram() y geom_freqpoly() mostrar la distribución de variables continuas.
geom_bar() muestra la distribución de variables categóricas.
geom_path() y geom_line() dibujan líneas entre los puntos de datos. Un gráfico de líneas está obligado a producir líneas que viajan de izquierda a derecha, mientras que los caminos pueden ir en cualquier dirección. Las líneas se suelen utilizar para explorar cómo cambian las cosas con el tiempo.

2.6.1 Agregar un suavizado a una gráfica

Si tiene un diagrama de dispersión con mucho ruido, puede resultar difícil ver el patrón dominante. En este caso es útil agregar una línea suavizada al gráfico con geom_smooth():

ggplot(mpg, aes(displ, hwy)) + 
  geom_point() + 
  geom_smooth()
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'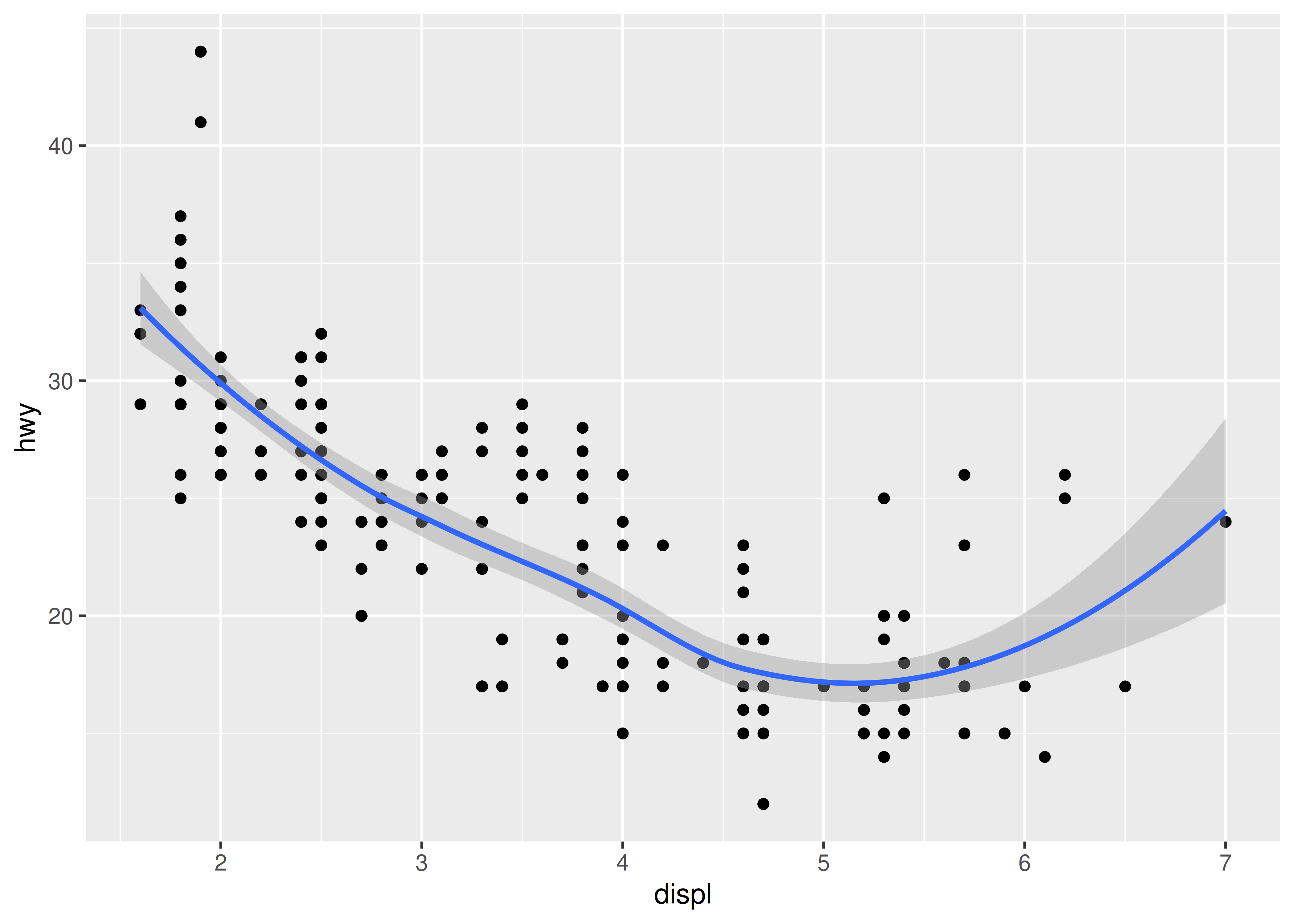

Esto superpone el diagrama de dispersión con una curva suave, que incluye una evaluación de la incertidumbre en forma de intervalos de confianza puntuales que se muestran en gris. Si no está interesado en el intervalo de confianza, desactívelo con geom_smooth(se = FALSE).

Un argumento importante para geom_smooth() es el método, que le permite elegir qué tipo de modelo se utiliza para ajustarse a la curva suave:

method = "loess", el valor predeterminado para n pequeña, utiliza una regresión local suave (como se describe en ?loess). El movimiento de la línea está controlado por el parámetro span, que varía de 0 (extremadamente ondulado) a 1 (no tan ondulado).
```
ggplot(mpg, aes(displ, hwy)) + 
  geom_point() + 
  geom_smooth(span = 0.2)
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'

ggplot(mpg, aes(displ, hwy)) + 
  geom_point() + 
  geom_smooth(span = 1)
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'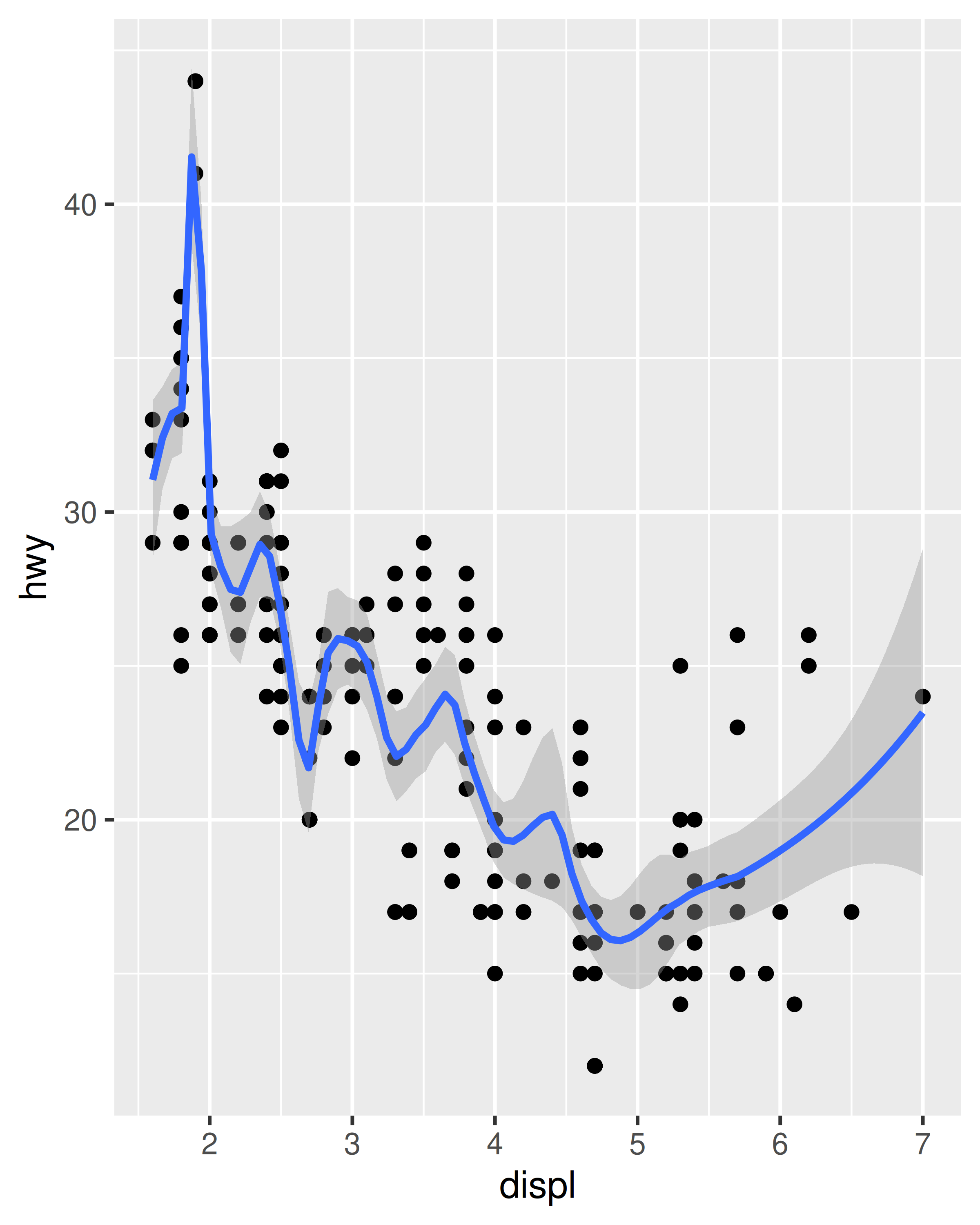
```
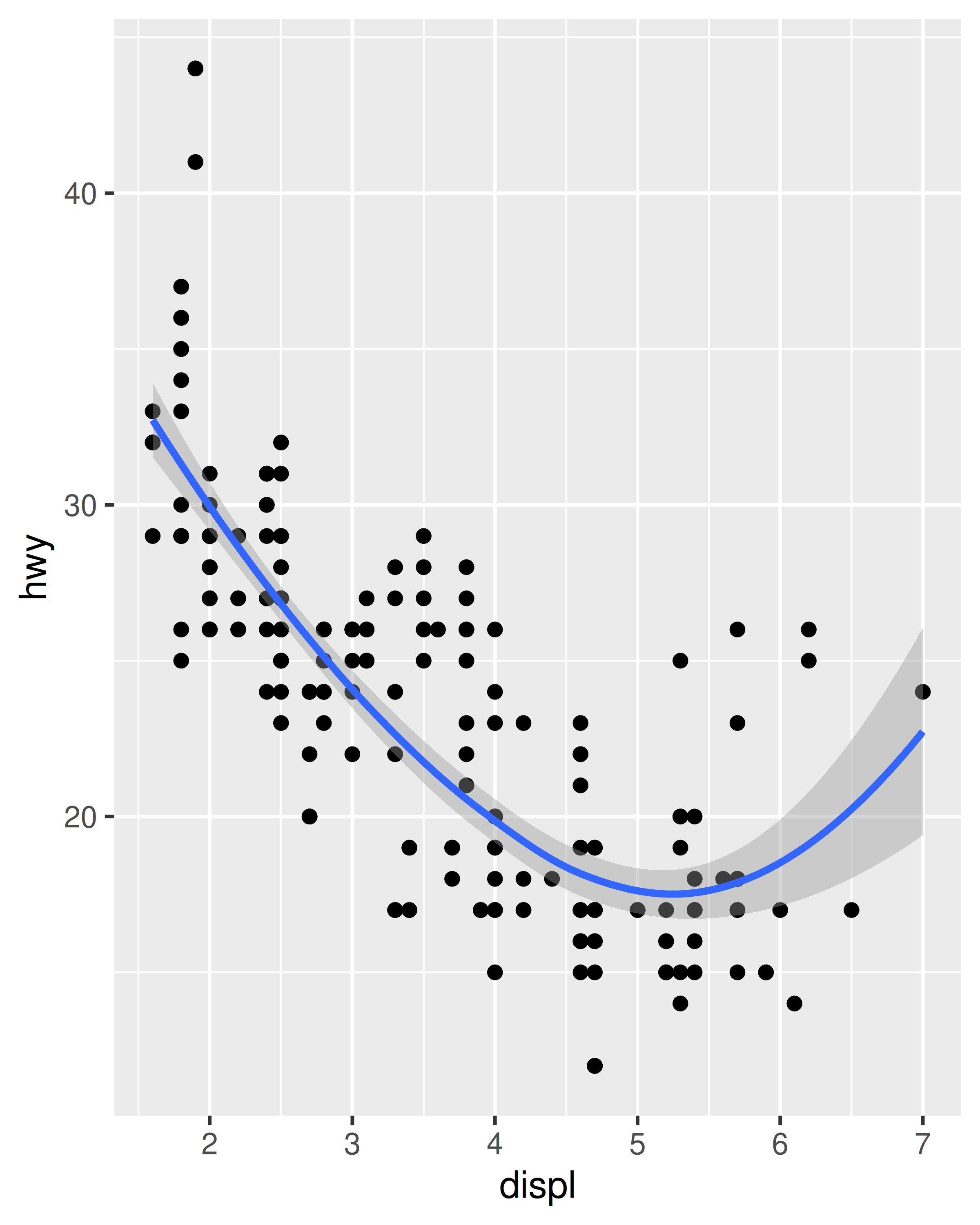
Loess no funciona bien para conjuntos de datos grandes (es \(O(n^2)\) en la memoria), por lo que se utiliza un algoritmo de suavizado alternativo cuando \(n\) es mayor que 1000.
method = "gam" Se ajusta a un modelo aditivo generalizado proporcionado por el paquete mgcv. Primero debe cargar mgcv, luego usar una fórmula como fórmula = y ~ s(x) o y ~ s(x, bs = "cs") (para datos grandes). Esto es lo que usa ggplot2 cuando hay más de 1000 puntos.
```
library(mgcv)
ggplot(mpg, aes(displ, hwy)) + 
  geom_point() + 
  geom_smooth(method = "gam", formula = y ~ s(x))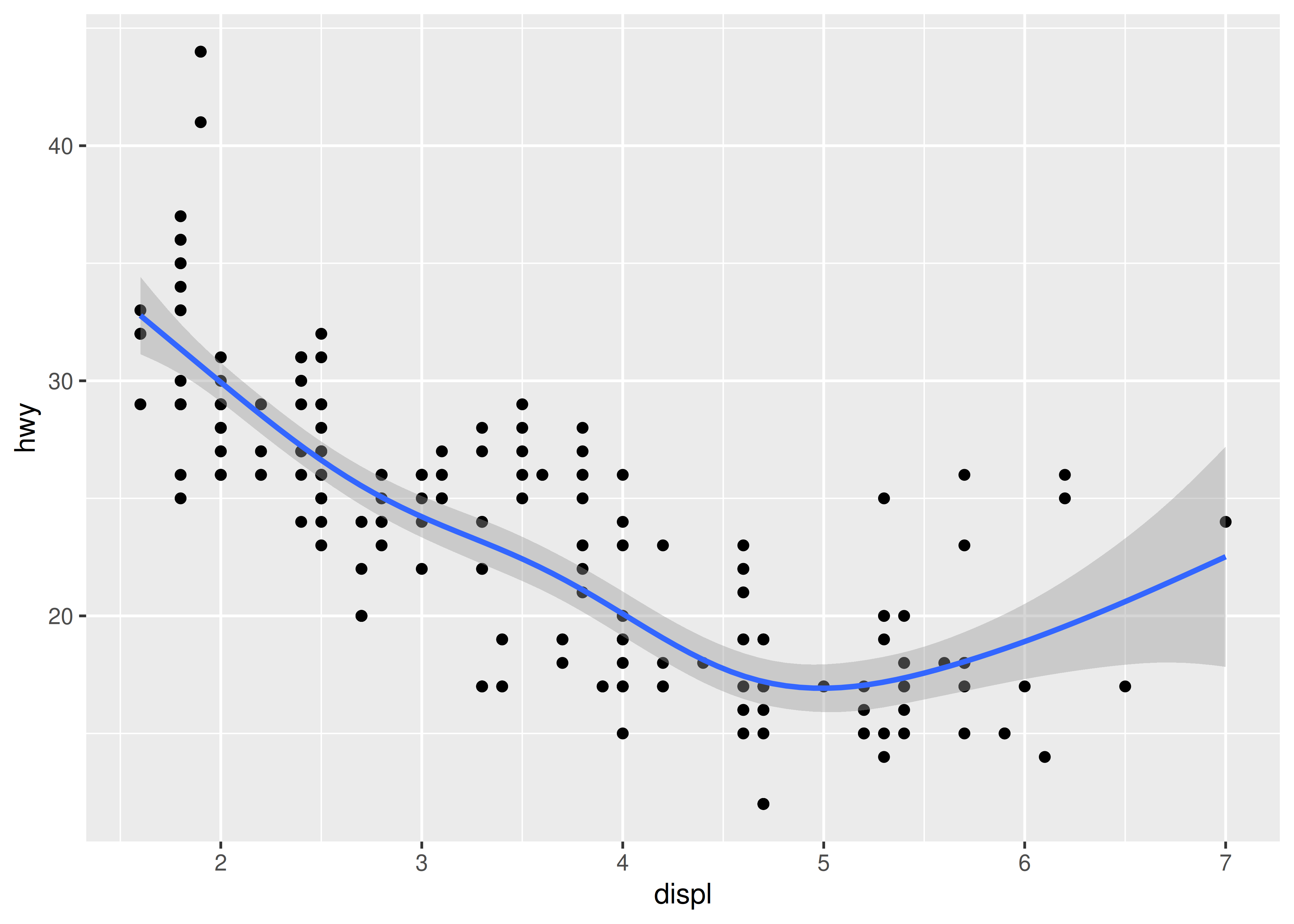
```

method = "lm" Se ajusta a un modelo lineal, dando la línea de mejor ajuste.

ggplot(mpg, aes(displ, hwy)) + 
  geom_point() + 
  geom_smooth(method = "lm")
#> `geom_smooth()` using formula = 'y ~ x'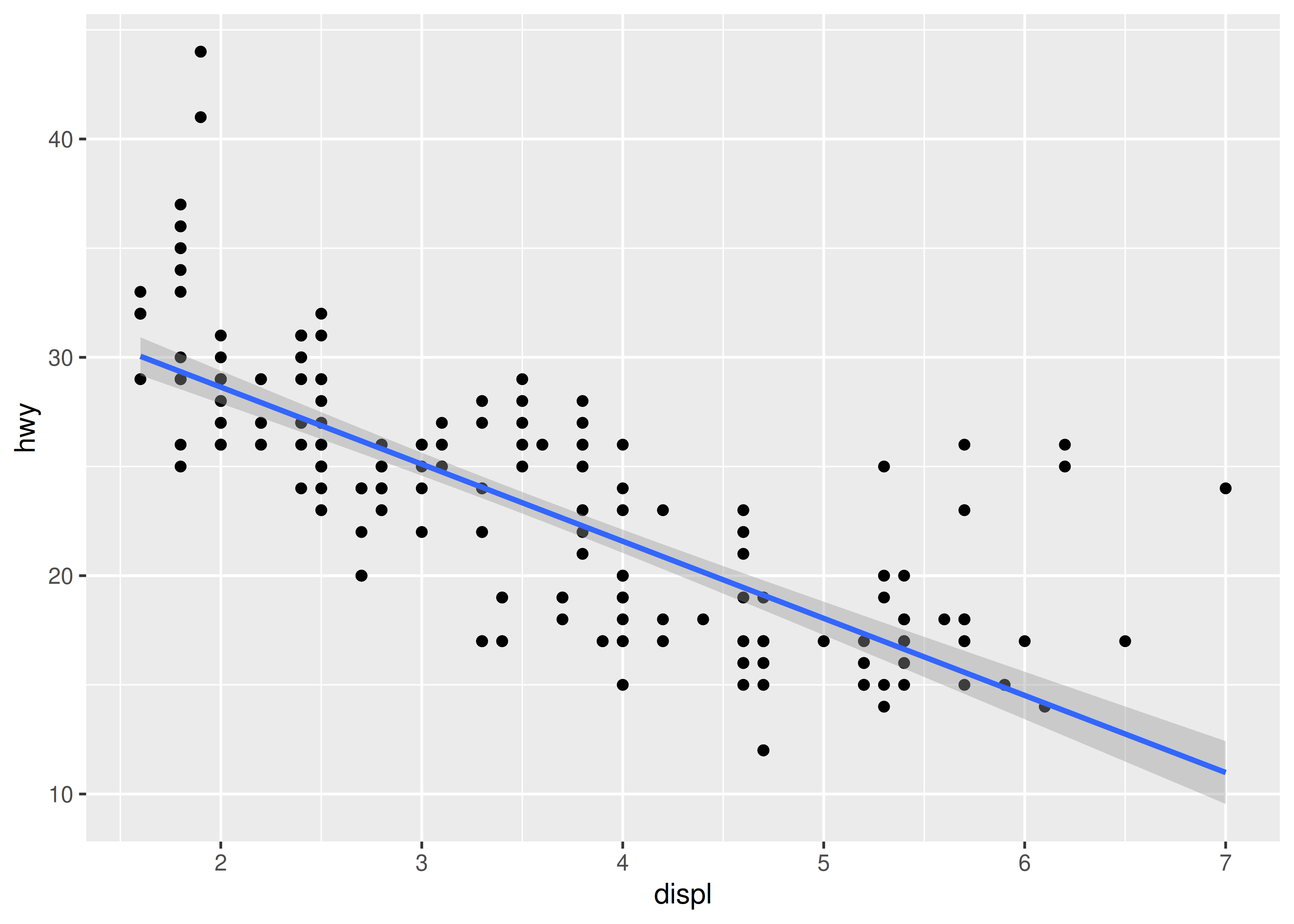

method = "rlm" funciona como lm(), pero utiliza un algoritmo de ajuste robusto para que los valores atípicos no afecten tanto el ajuste. Es parte del paquete MASS, así que recuerda cargarlo primero.

2.6.2 Diagramas de caja y puntos nerviosos

Cuando un conjunto de datos incluye una variable categórica y una o más variables continuas, probablemente le interesará saber cómo varían los valores de las variables continuas con los niveles de la variable categórica. Digamos que estamos interesados en ver cómo varía la economía de combustible dentro de los automóviles que tienen el mismo tipo de transmisión. Podríamos comenzar con un diagrama de dispersión como este:

ggplot(mpg, aes(drv, hwy)) + 
  geom_point()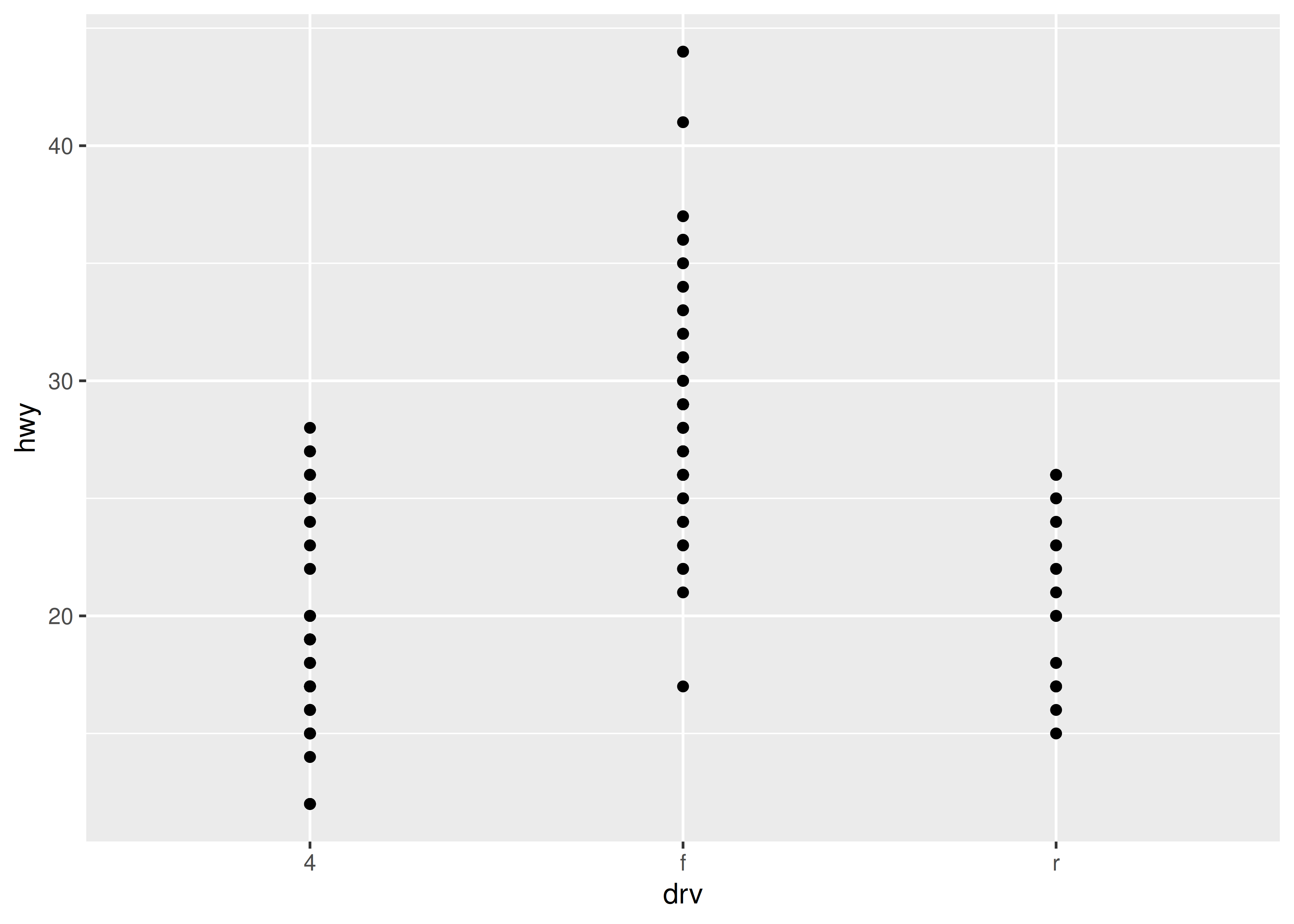

Debido a que hay pocos valores únicos tanto para drv como para hwy, hay mucho trazado excesivo. Muchos puntos están trazados en la misma ubicación y es difícil ver la distribución. Hay tres técnicas útiles que ayudan a aliviar el problema:

El jittering, geom_jitter(), añade un poco de ruido aleatorio a los datos, lo que puede ayudar a evitar el trazado excesivo.
Los diagramas de caja, geom_boxplot(), resumen la forma de la distribución con un puñado de estadísticas resumidas.
Los gráficos de violín, geom_violin(), muestran una representación compacta de la “densidad” de la distribución, resaltando las áreas donde se encuentran más puntos.

Estos se ilustran a continuación:

ggplot(mpg, aes(drv, hwy)) + geom_jitter()
ggplot(mpg, aes(drv, hwy)) + geom_boxplot()
ggplot(mpg, aes(drv, hwy)) + geom_violin()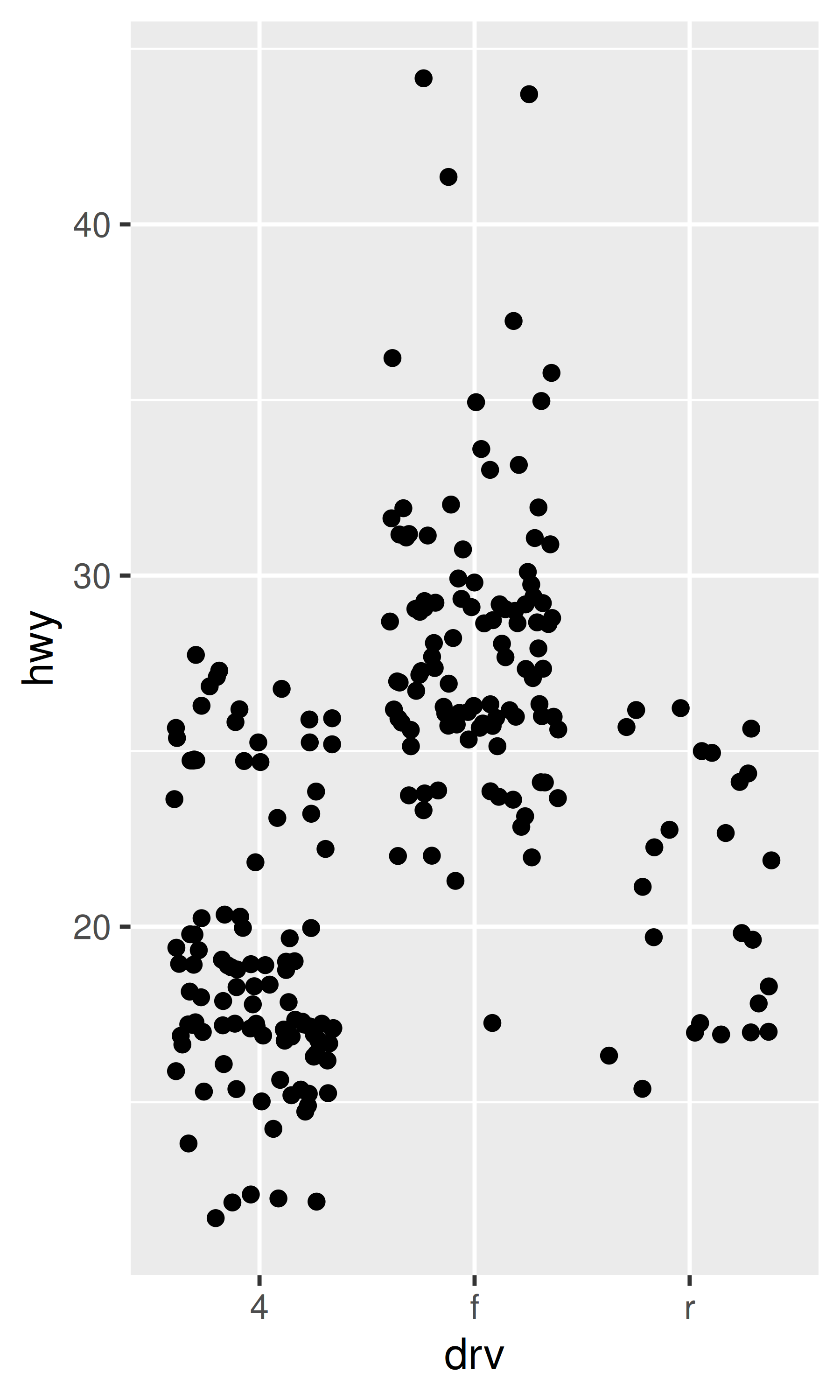

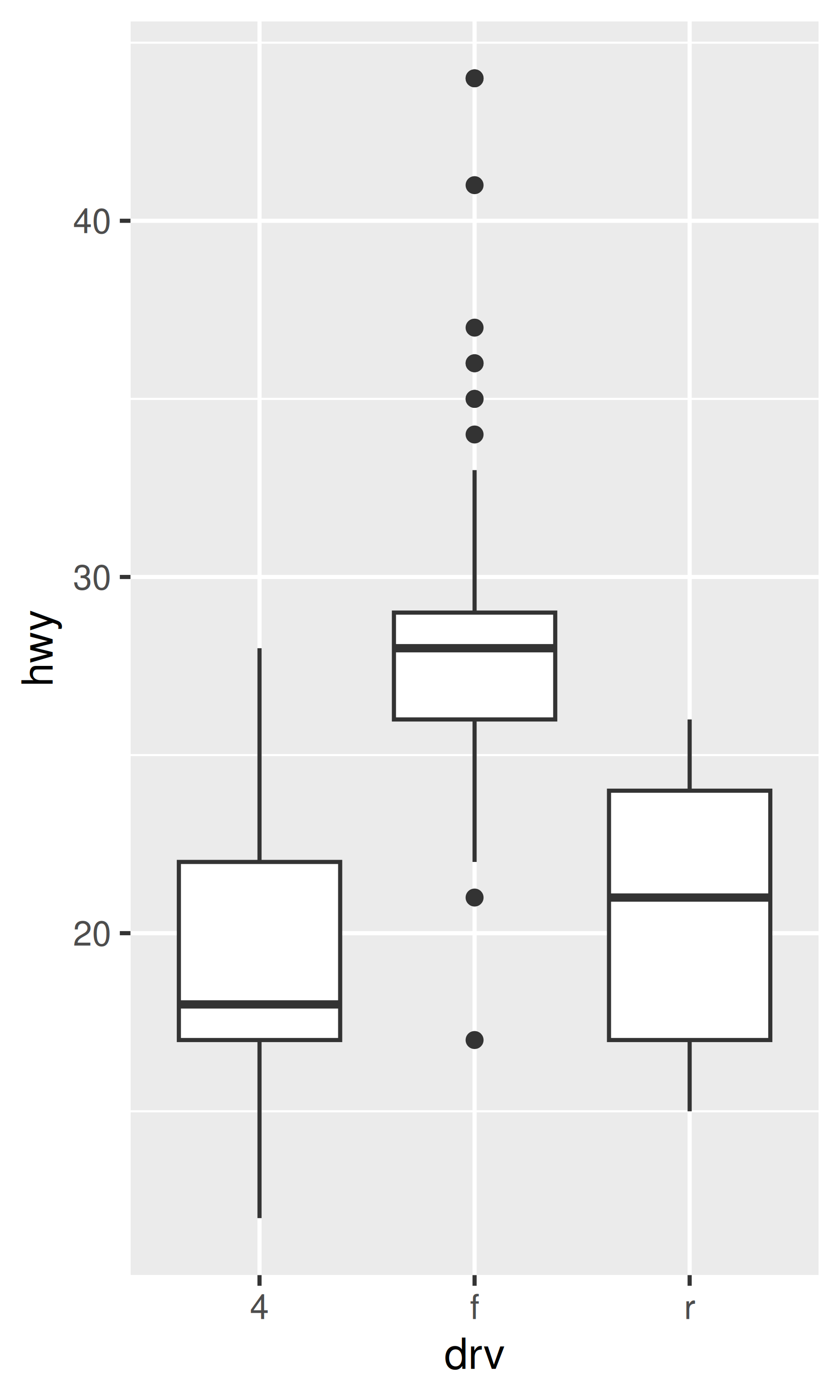
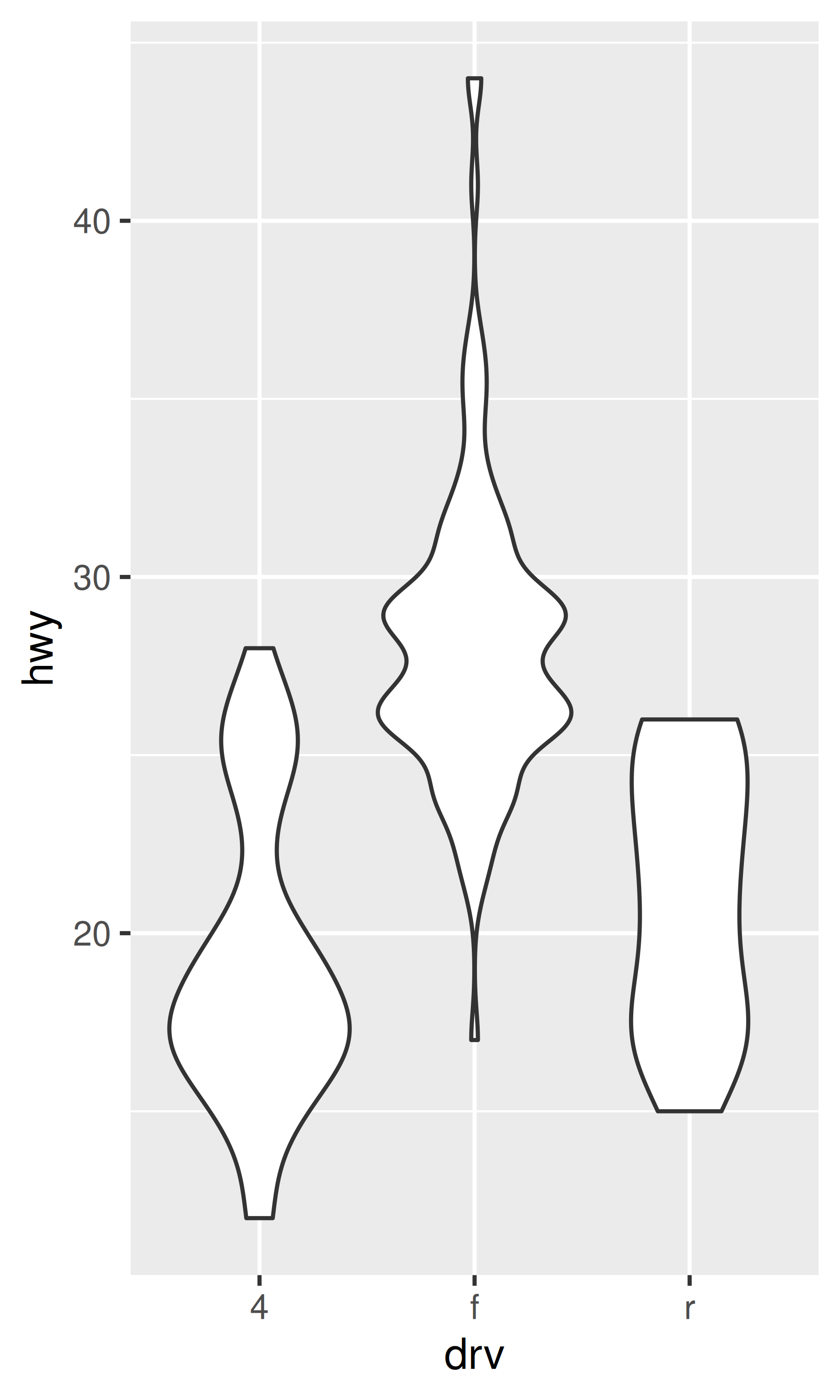
Cada método tiene sus fortalezas y debilidades. Los diagramas de caja resumen la mayor parte de la distribución con solo cinco números, mientras que los diagramas con fluctuaciones muestran cada punto pero solo funcionan con conjuntos de datos relativamente pequeños. Los gráficos de violín ofrecen la visualización más rica, pero se basan en el cálculo de una estimación de densidad, que puede ser difícil de interpretar.

Para puntos nerviosos, geom_jitter() ofrece el mismo control sobre la estética que geom_point(): size, colour y shape. Para geom_boxplot() y geom_violin(), puedes controlar el color del contorno colour o el color interno del fill.

2.6.3 Histogramas y polígonos de frecuencia.

Los histogramas y los polígonos de frecuencia muestran la distribución de una única variable numérica. Proporcionan más información sobre la distribución de un solo grupo que los diagramas de caja, a costa de necesitar más espacio.

ggplot(mpg, aes(hwy)) + geom_histogram()
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
ggplot(mpg, aes(hwy)) + geom_freqpoly()
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.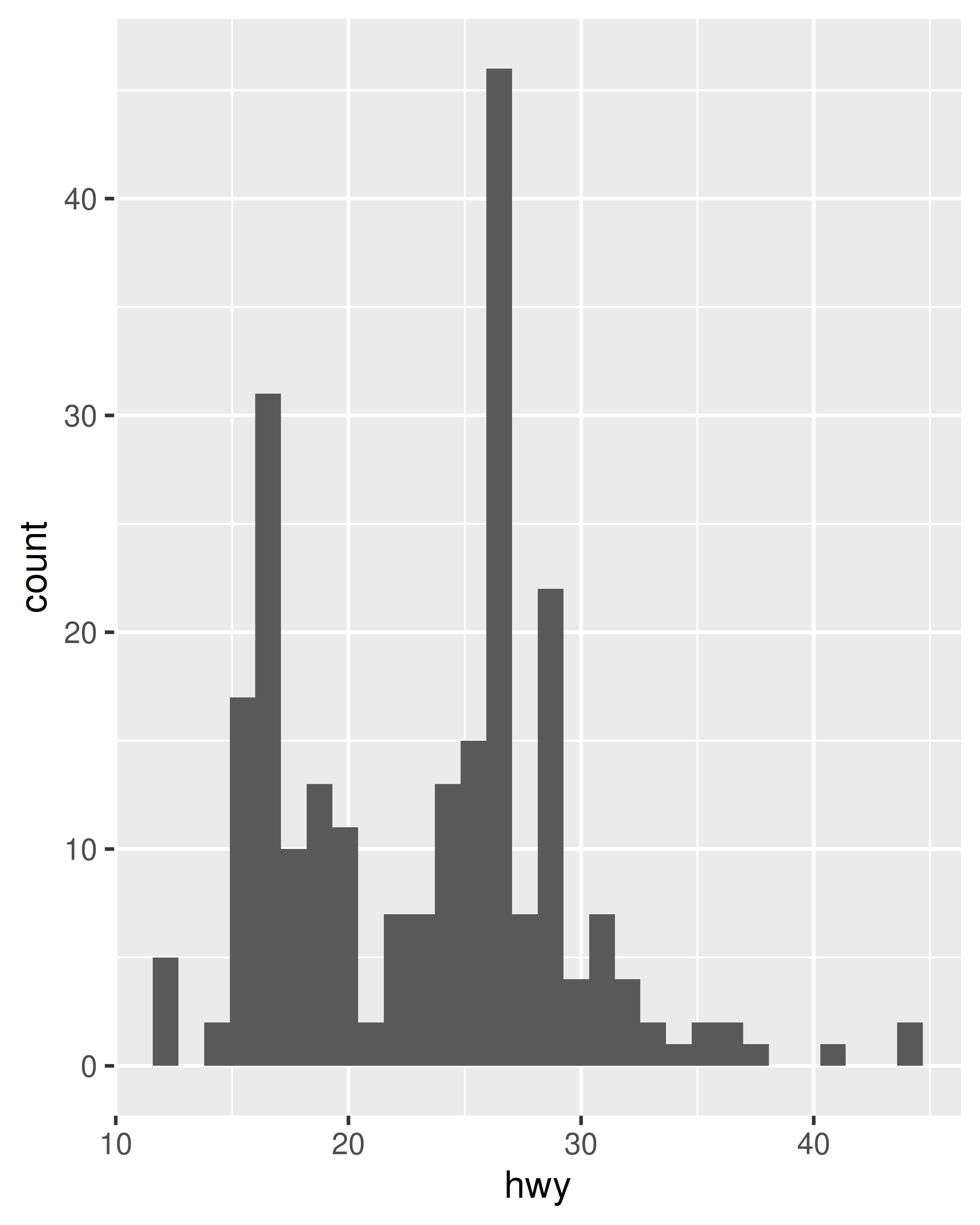

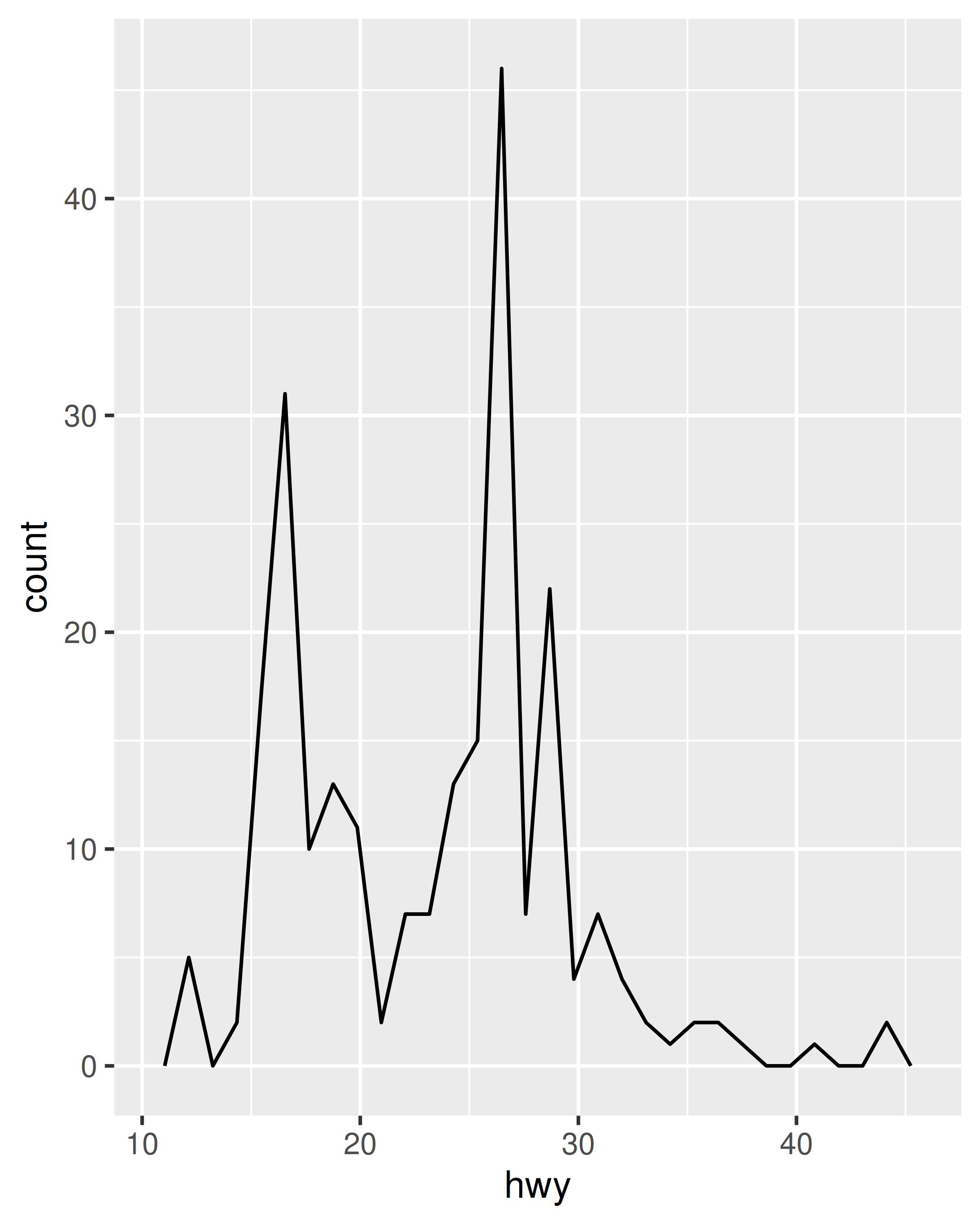
Tanto los histogramas como los polígonos de frecuencia funcionan de la misma manera: agrupan los datos y luego cuentan el número de observaciones en cada contenedor. La única diferencia es la visualización: los histogramas usan barras y los polígonos de frecuencia usan líneas.

Puede controlar el ancho de los contenedores con el argumento binwidth (si no desea contenedores espaciados uniformemente, puede usar el argumento breaks). Es muy importante experimentar con el ancho del contenedor. El valor predeterminado simplemente divide sus datos en 30 contenedores, lo que probablemente no sea la mejor opción. Siempre debe probar con muchos anchos de bin y es posible que necesite varios anchos de bin para contar la historia completa de sus datos.

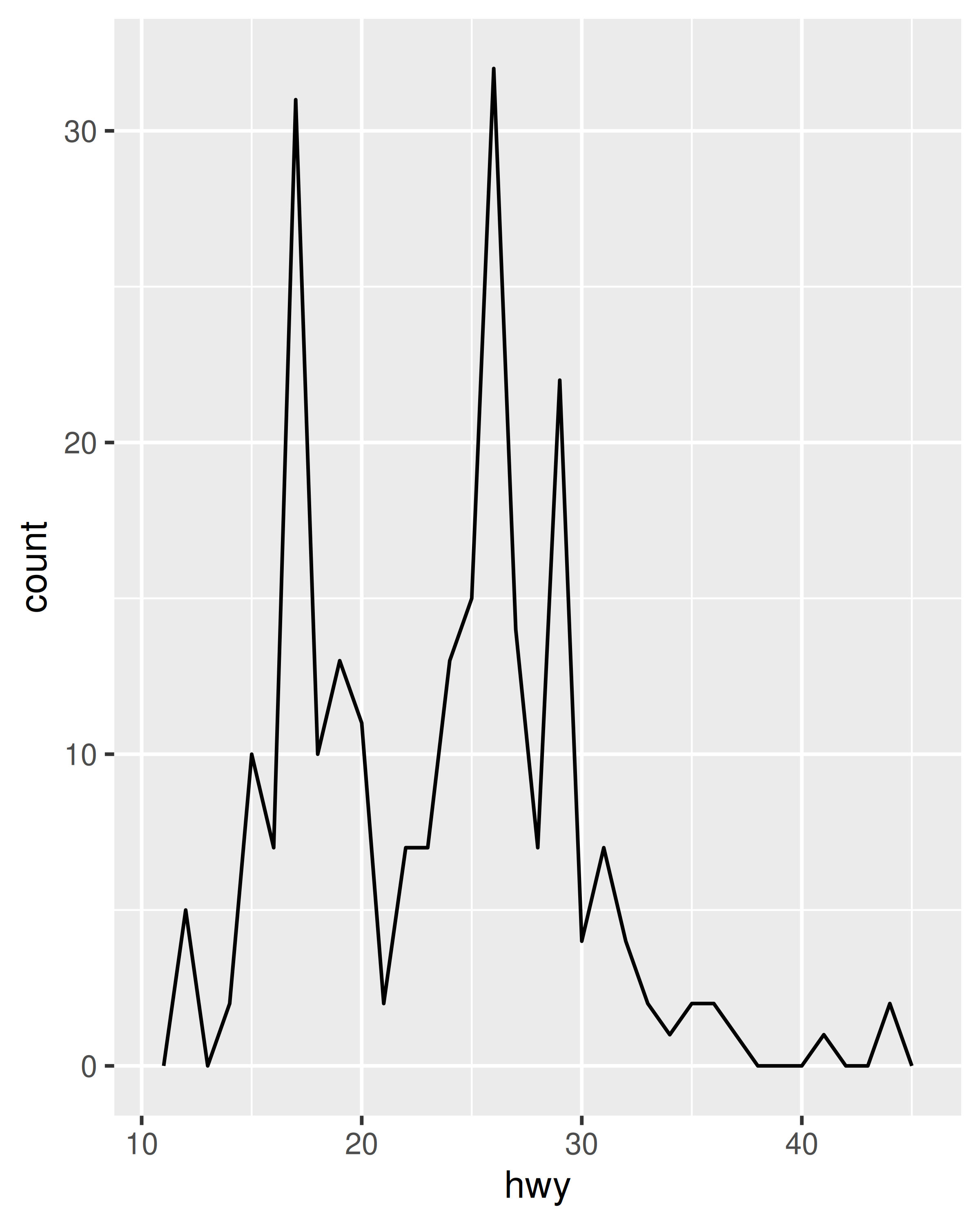
ggplot(mpg, aes(hwy)) + 
  geom_freqpoly(binwidth = 2.5)
ggplot(mpg, aes(hwy)) + 
  geom_freqpoly(binwidth = 1)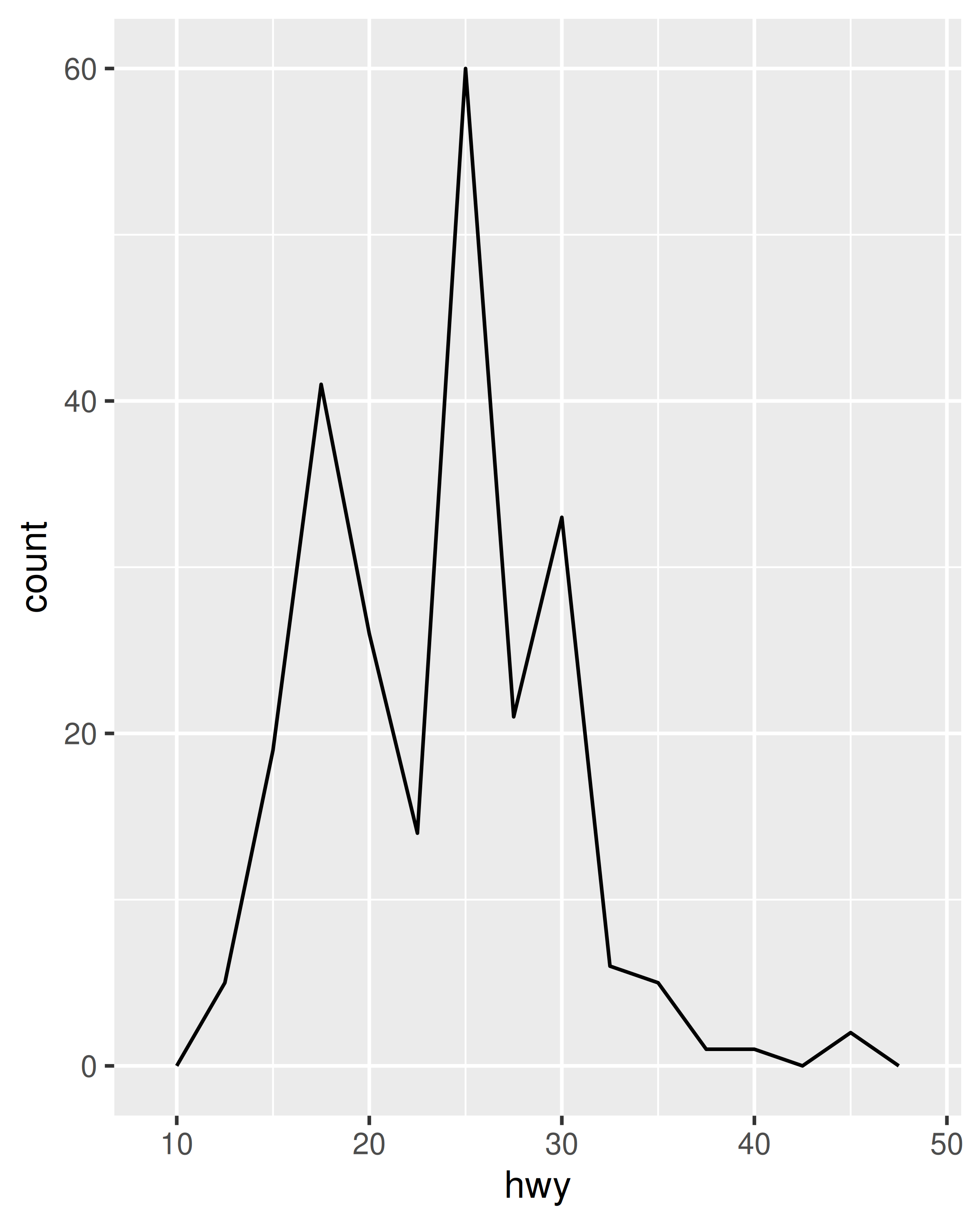

Una alternativa al polígono de frecuencia es el gráfico de densidad, geom_density(). Se requiere un poco de cuidado si se utilizan gráficos de densidad: en comparación con los polígonos de frecuencia, son más difíciles de interpretar ya que los cálculos subyacentes son más complejos. También hacen suposiciones que no son ciertas para todos los datos, a saber, que la distribución subyacente es continua, ilimitada y suave.

Para comparar las distribuciones de diferentes subgrupos, puede asignar una variable categórica a relleno (para geom_histogram()) o color (para geom_freqpoly()). Es más fácil comparar distribuciones usando el polígono de frecuencia porque la tarea de percepción subyacente es más sencilla. También puedes usar facetas: esto dificulta un poco las comparaciones, pero es más fácil ver la distribución de cada grupo.

ggplot(mpg, aes(displ, colour = drv)) + 
  geom_freqpoly(binwidth = 0.5)
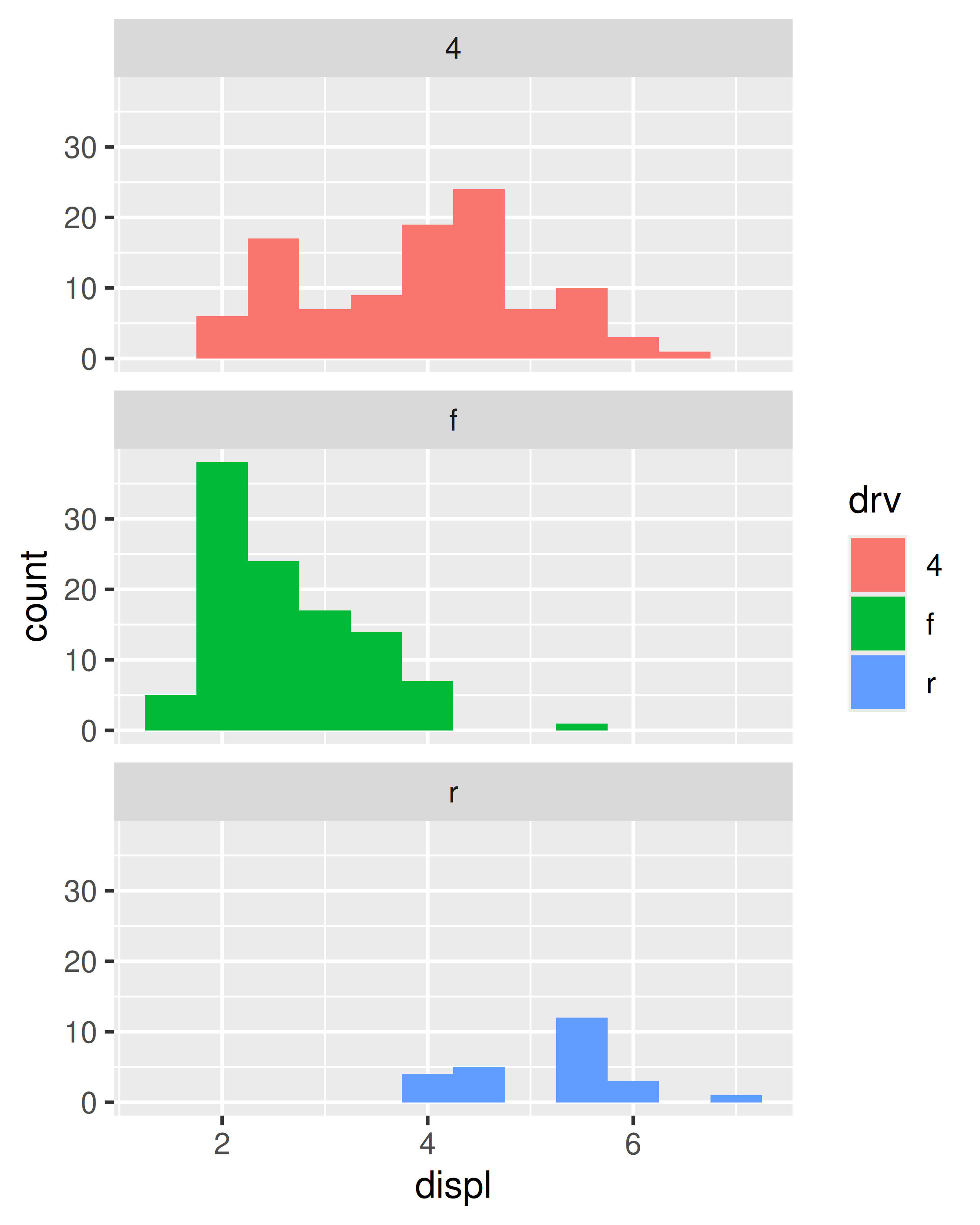
ggplot(mpg, aes(displ, fill = drv)) + 
  geom_histogram(binwidth = 0.5) + 
  facet_wrap(~drv, ncol = 1)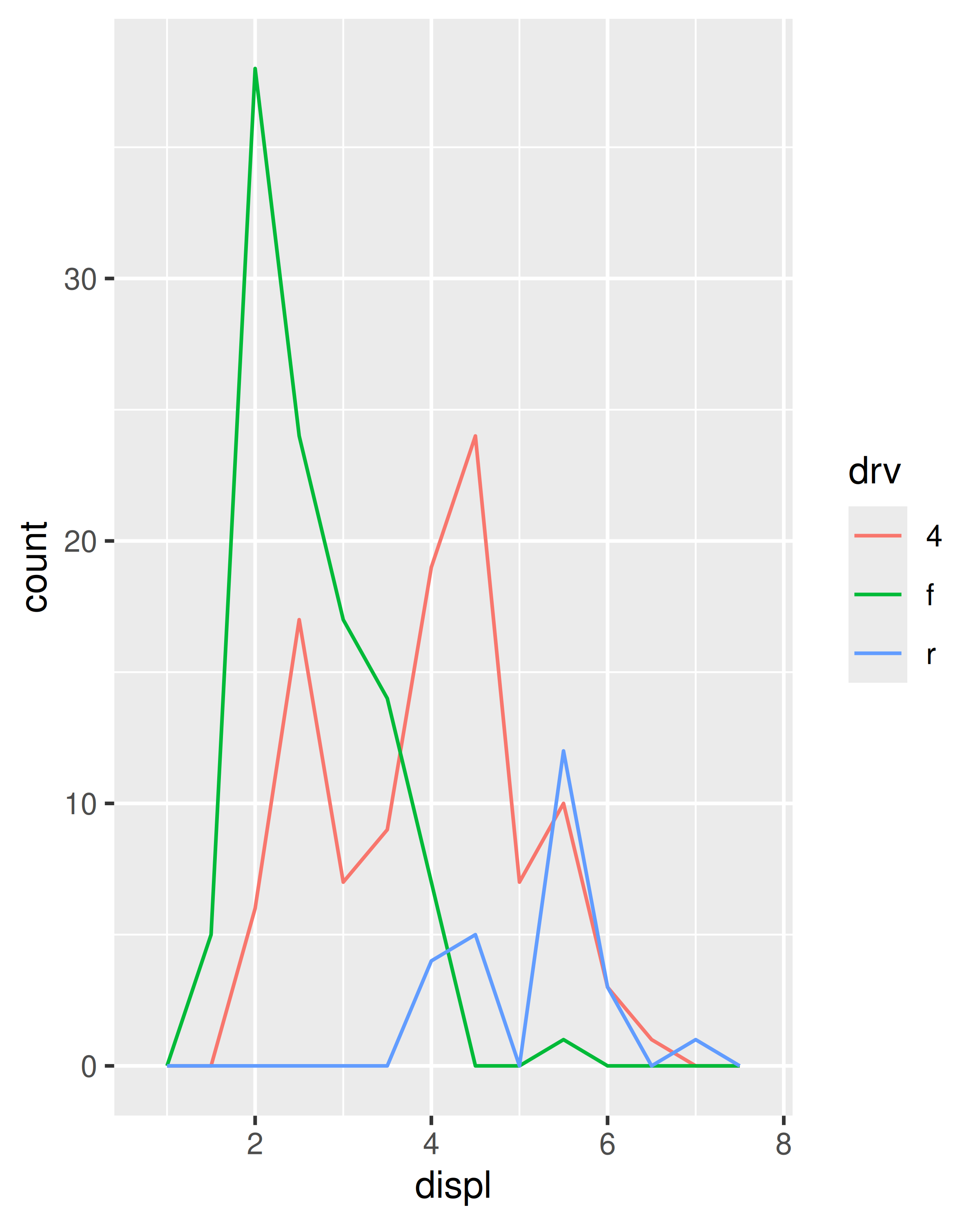

2.6.4 Gráfica de barras

El análogo discreto del histograma es el gráfico de barras, geom_bar(). Es fácil de usar:

ggplot(mpg, aes(manufacturer)) + 
  geom_bar()

(Aprenderás cómo arreglar las etiquetas en Sección 17.4.2).

Los gráficos de barras pueden resultar confusos porque hay dos gráficos bastante diferentes que comúnmente se denominan gráficos de barras. El formulario anterior espera que tenga datos no resumidos y cada observación contribuye con una unidad a la altura de cada barra. La otra forma de gráfico de barras se utiliza para datos presumidos. Por ejemplo, es posible que tenga tres medicamentos con su efecto promedio:

drugs <- data.frame(
  drug = c("a", "b", "c"),
  effect = c(4.2, 9.7, 6.1)
)

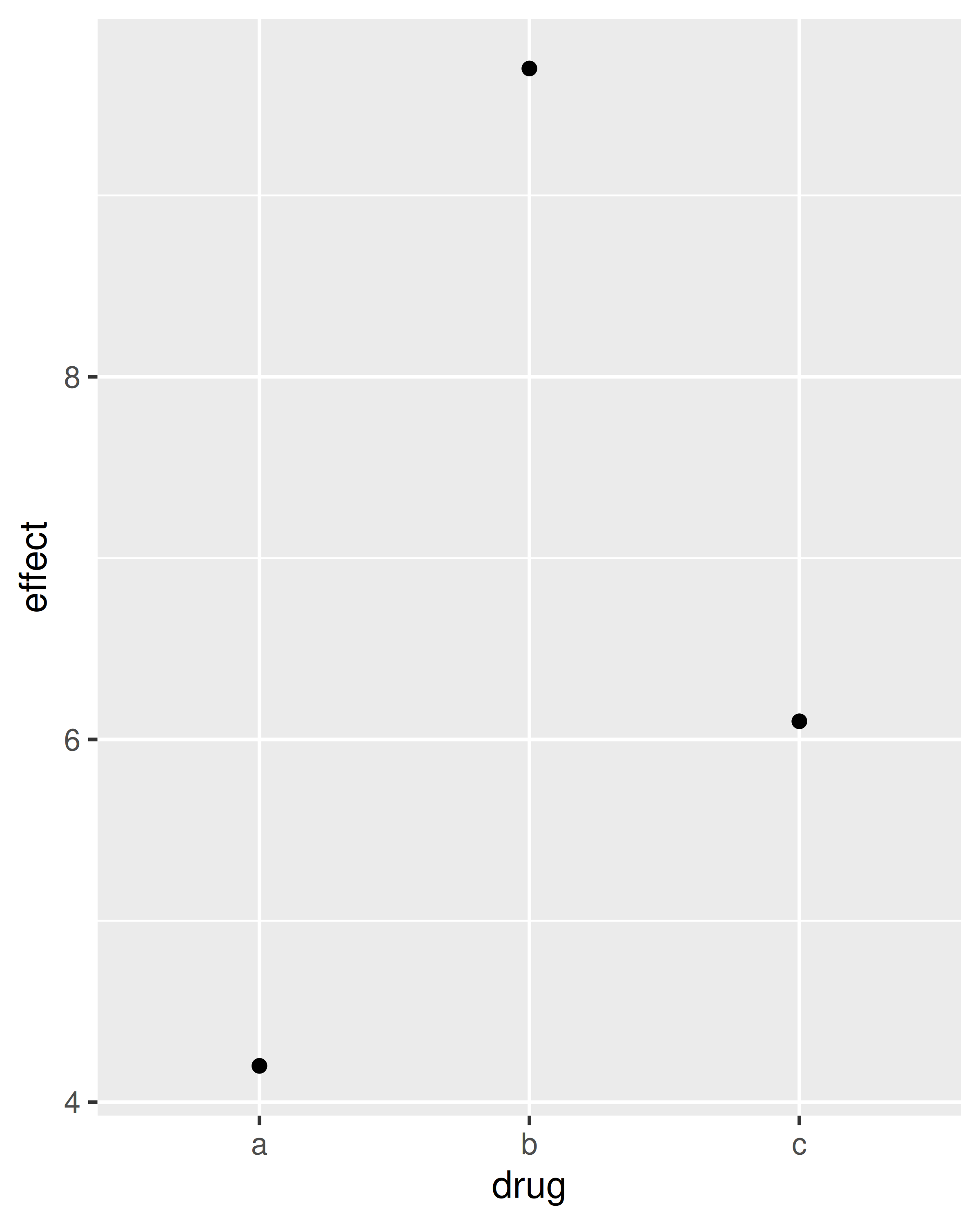
Para mostrar este tipo de datos, debe decirle a geom_bar() que no ejecute la estadística predeterminada que agrupa y cuenta los datos. Sin embargo, creemos que es incluso mejor usar geom_point() porque los puntos ocupan menos espacio que las barras y no requieren que el eje y incluya 0.

ggplot(drugs, aes(drug, effect)) + geom_bar(stat = "identity")
ggplot(drugs, aes(drug, effect)) + geom_point()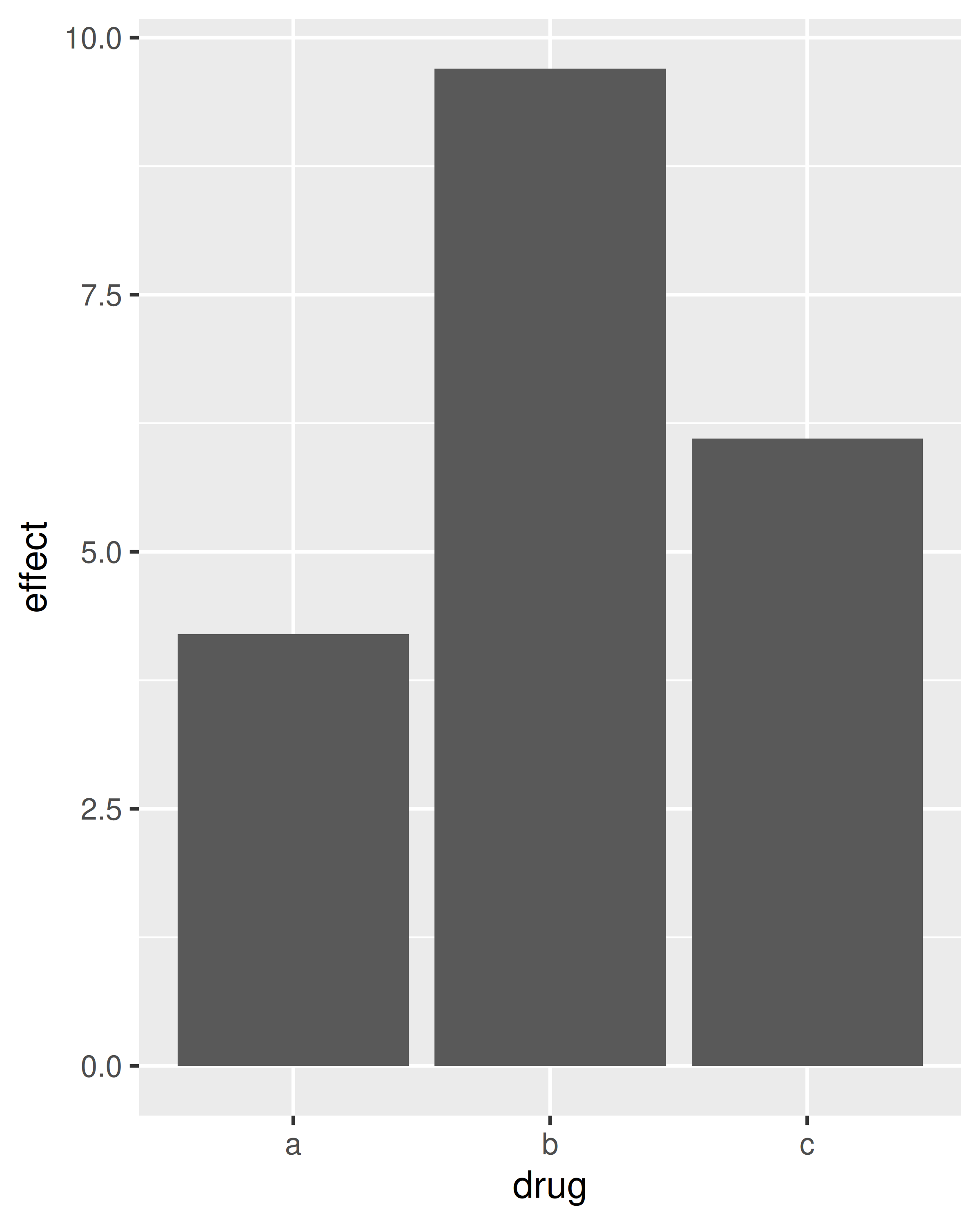

2.6.5 Series de tiempo con gráficos de líneas y rutas

Los gráficos de líneas y rutas se utilizan normalmente para datos de series temporales. Los diagramas de líneas unen los puntos de izquierda a derecha, mientras que los diagramas de ruta los unen en el orden en que aparecen en el conjunto de datos (en otras palabras, un diagrama de líneas es un diagrama de ruta de los datos ordenados por valor de x). Los gráficos de líneas generalmente tienen el tiempo en el eje x, lo que muestra cómo una sola variable ha cambiado con el tiempo. Los gráficos de ruta muestran cómo dos variables han cambiado simultáneamente a lo largo del tiempo, con el tiempo codificado en la forma en que se conectan las observaciones.

Debido a que la variable año en el conjunto de datos mpg solo tiene dos valores, mostraremos algunos gráficos de series temporales utilizando el conjunto de datos economics, que contiene datos económicos sobre los EE. UU. medidos durante los últimos 40 años. La siguiente figura muestra dos gráficos de desempleo a lo largo del tiempo, ambos producidos usando geom_line(). El primero muestra la tasa de desempleo mientras que el segundo muestra la mediana del número de semanas desempleadas. Ya podemos ver algunas diferencias en estas dos variables, particularmente en el último pico, donde el porcentaje de desempleo es menor que en los picos anteriores, pero la duración del desempleo es alta.

ggplot(economics, aes(date, unemploy / pop)) +
  geom_line()
ggplot(economics, aes(date, uempmed)) +
  geom_line()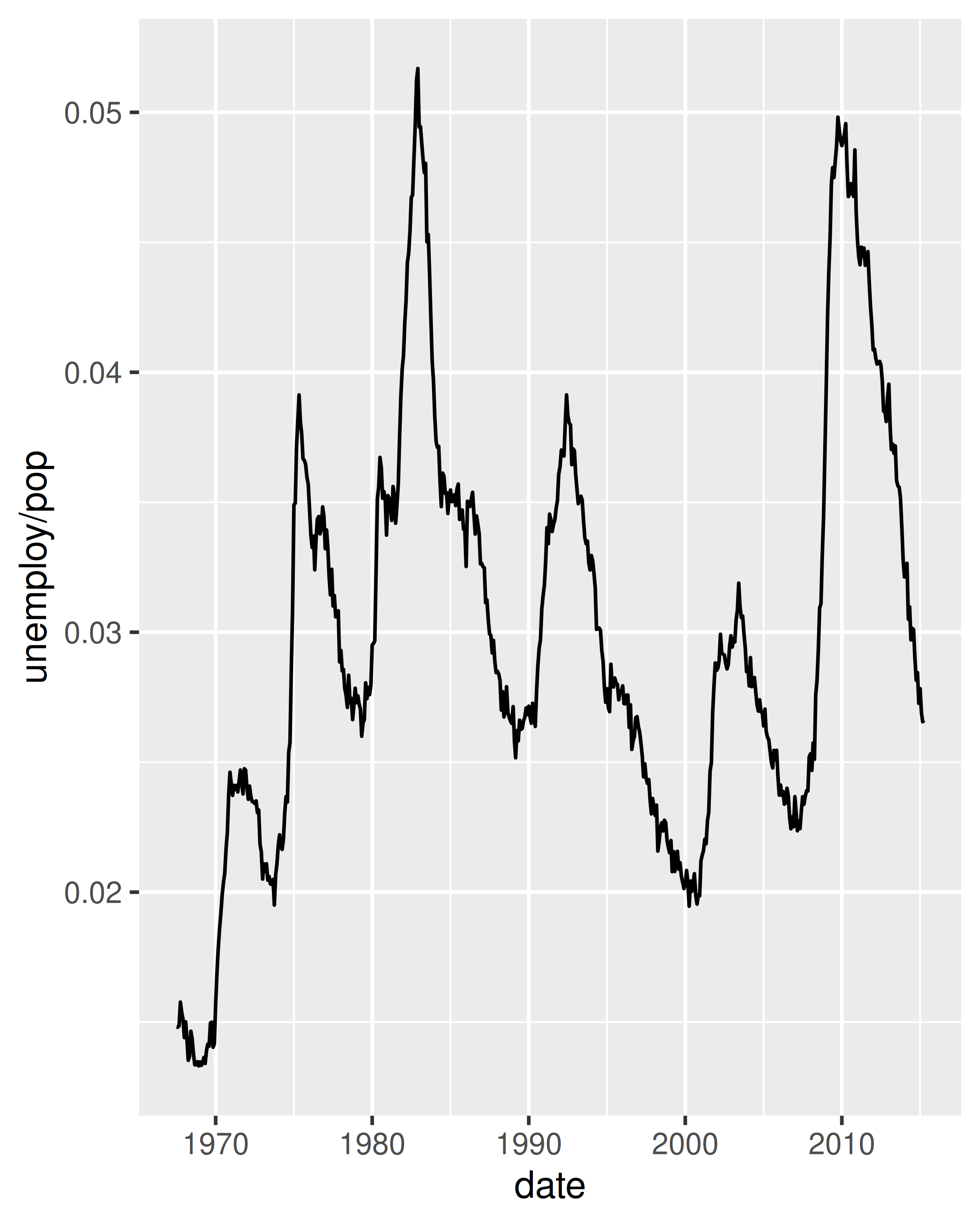

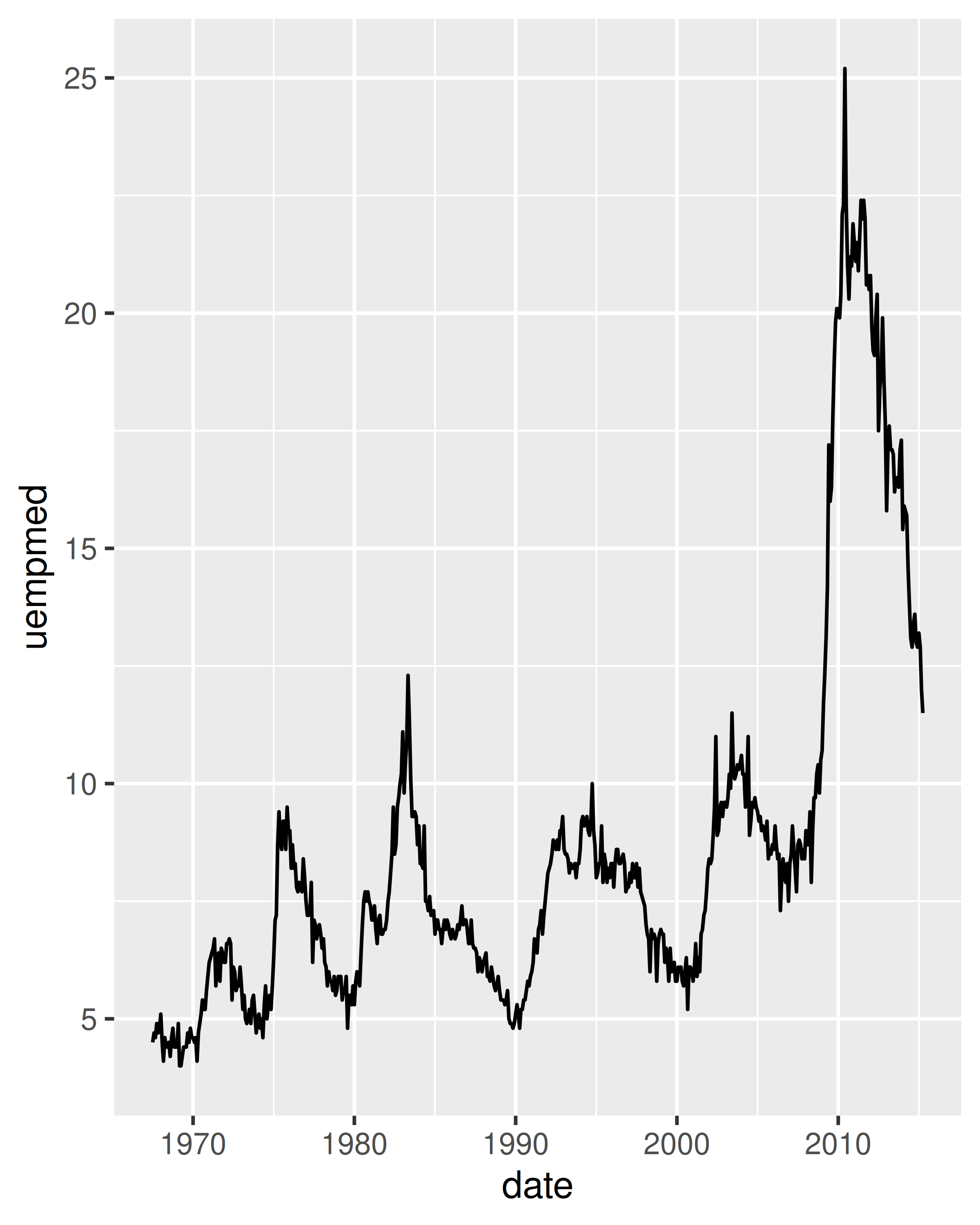
Para examinar esta relación con mayor detalle, nos gustaría dibujar ambas series de tiempo en la misma gráfica. Podríamos dibujar un diagrama de dispersión de la tasa de desempleo versus la duración del desempleo, pero entonces ya no podríamos ver la evolución en el tiempo. La solución es unir puntos adyacentes en el tiempo con segmentos de línea, formando un trazado de ruta.

A continuación graficamos la tasa de desempleo versus la duración del desempleo y unimos las observaciones individuales con una trayectoria. Debido a los muchos cruces de líneas, la dirección en la que fluye el tiempo no es fácil de ver en la primera gráfica. En el segundo gráfico, coloreamos los puntos para que sea más fácil ver la dirección del tiempo.

ggplot(economics, aes(unemploy / pop, uempmed)) + 
  geom_path() +
  geom_point()

year <- function(x) as.POSIXlt(x)$year + 1900
ggplot(economics, aes(unemploy / pop, uempmed)) + 
  geom_path(colour = "grey50") +
  geom_point(aes(colour = year(date)))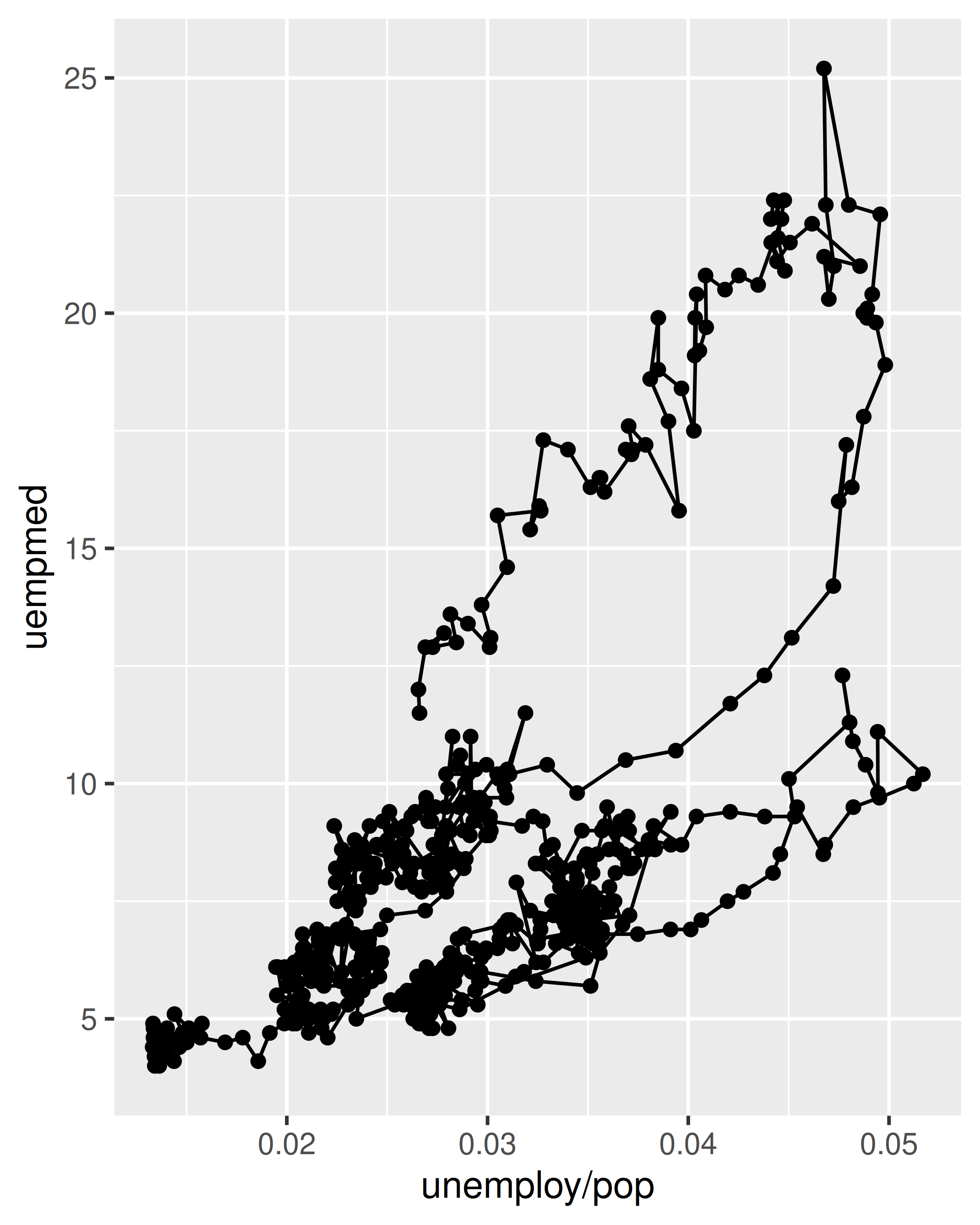

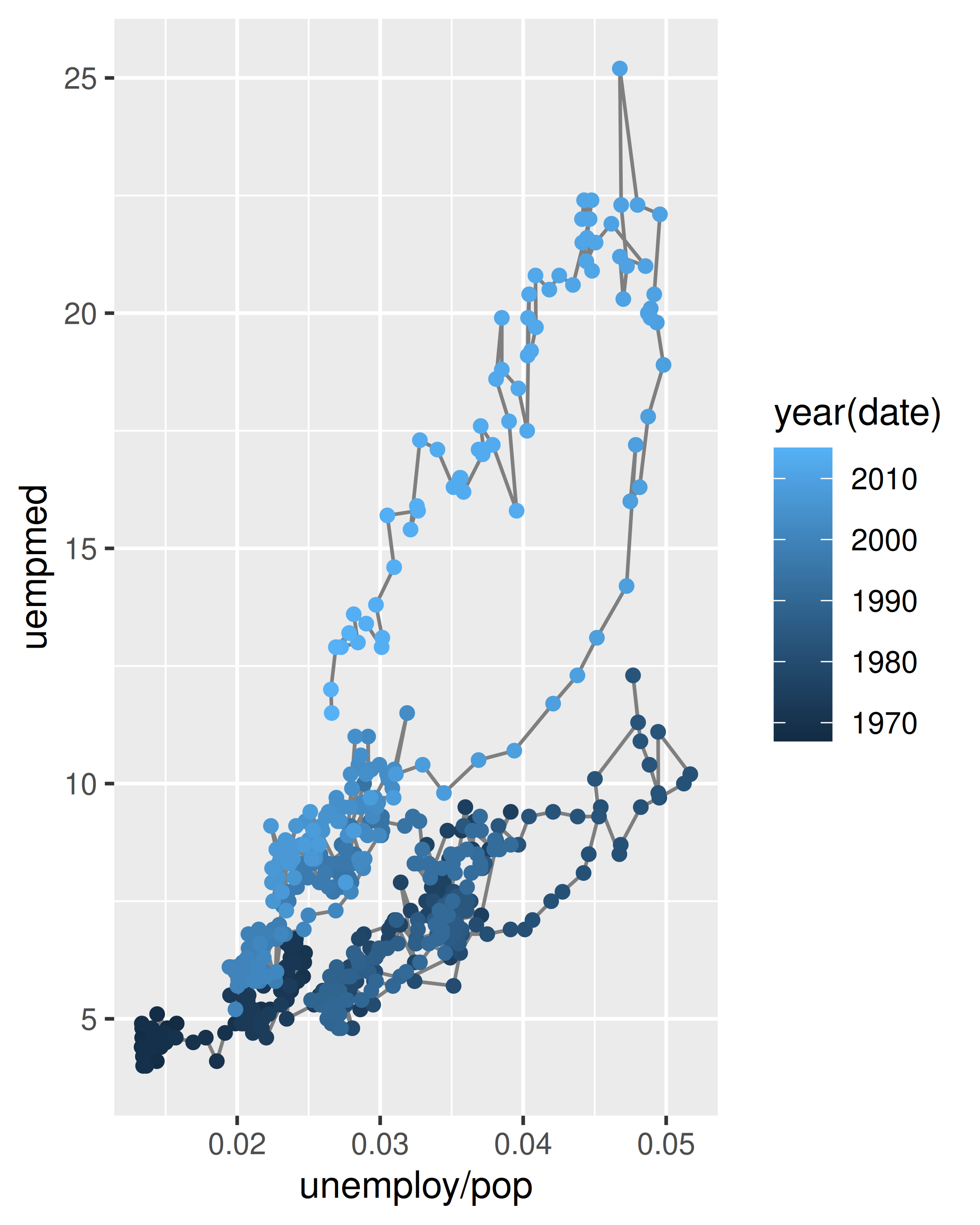
Podemos ver que la tasa de desempleo y la duración del desempleo están altamente correlacionadas, pero en los últimos años la duración del desempleo ha aumentado en relación con la tasa de desempleo.

Con datos longitudinales, a menudo desea mostrar varias series temporales en cada gráfico, donde cada serie representa a un individuo. Para hacer esto, necesita asignar la estética del group a una variable que codifique la membresía del grupo de cada observación. Esto se explica con más profundidad en Capítulo 4.

2.6.6 Ejercicios

¿Cuál es el problema con la gráfica creada por ggplot(mpg, aes(cty, hwy)) + geom_point()? ¿Cuál de las geoms descritas anteriormente es más eficaz para solucionar el problema?
Un desafío con ggplot(mpg, aes(class, hwy)) + geom_boxplot() es que el orden de class es alfabético, lo cual no es muy útil. ¿Cómo podrías cambiar los niveles de los factores para que sean más informativos?

En lugar de reordenar el factor manualmente, puede hacerlo automáticamente según los datos: ggplot(mpg, aes(reorder(class, hwy), hwy)) + geom_boxplot(). ¿Qué hace reordenar()? Lea la documentación.
Explore la distribución de la variable quilates en el conjunto de datos diamonds . ¿Qué ancho de contenedor revela los patrones más interesantes?
Explore la distribución de la variable precio en los datos de diamonds . ¿Cómo varía la distribución según el corte?
Ahora conoces (al menos) tres formas de comparar las distribuciones de subgrupos: geom_violin(), geom_freqpoly() y la estética del color, o geom_histogram() y facetado. ¿Cuáles son las fortalezas y debilidades de cada enfoque? ¿Qué otros enfoques podrías probar?
Lea la documentación de geom_bar(). ¿Qué hace la estética del weight ?
Utilizando las técnicas ya analizadas en este capítulo, piense en tres formas de visualizar una distribución categórica 2D. Pruébelos visualizando la distribución de model y manufacturer, trans y class, y cyl y trans.

2.7 Modificando los ejes

Aprenderá toda la gama de opciones disponibles en capítulos posteriores, pero dos familias de útiles ayudas le permitirán realizar las modificaciones más comunes. xlab() y ylab() modifican las etiquetas de los ejes x e y:

ggplot(mpg, aes(cty, hwy)) +
  geom_point(alpha = 1 / 3)

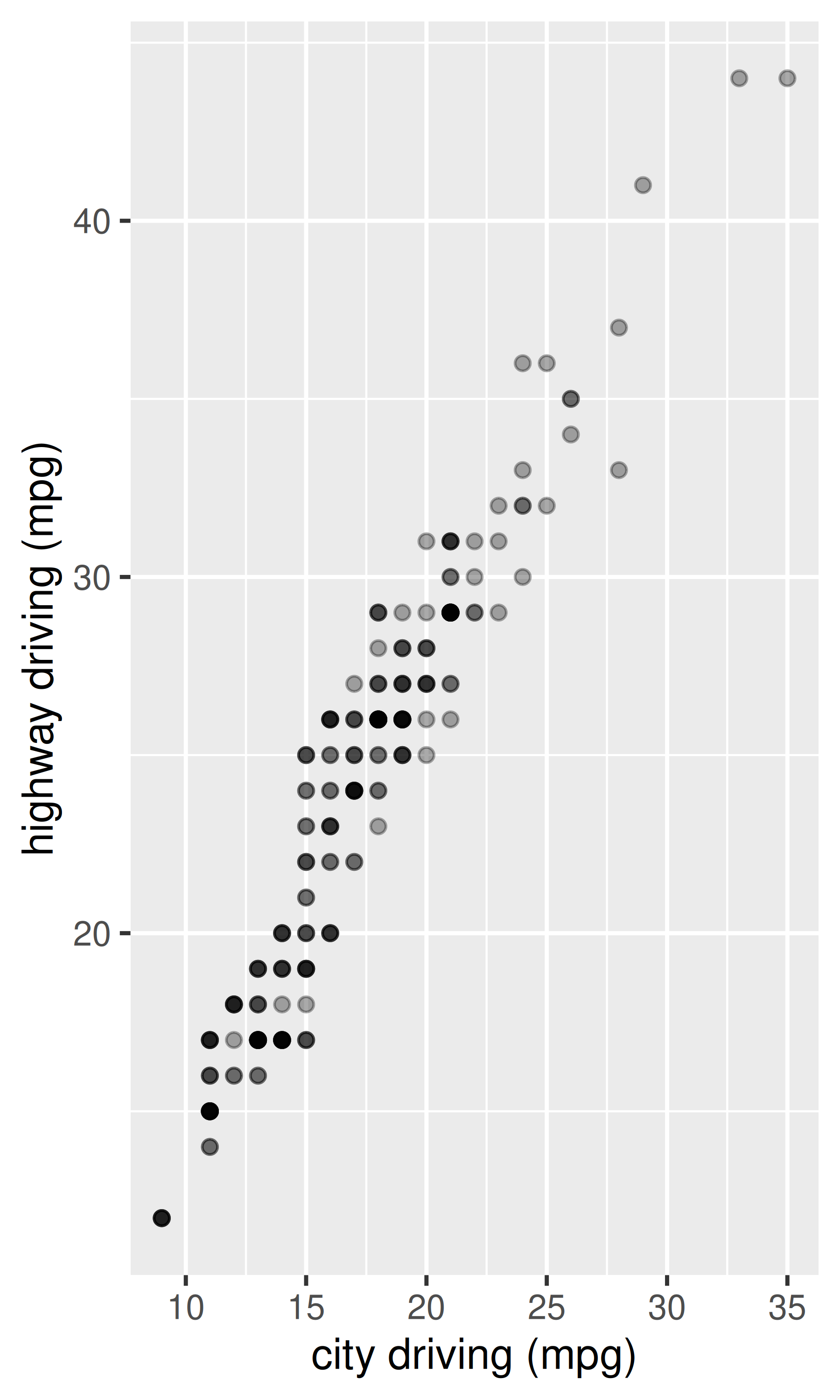
ggplot(mpg, aes(cty, hwy)) +
  geom_point(alpha = 1 / 3) + 
  xlab("city driving (mpg)") + 
  ylab("highway driving (mpg)")

# Remove the axis labels with NULL
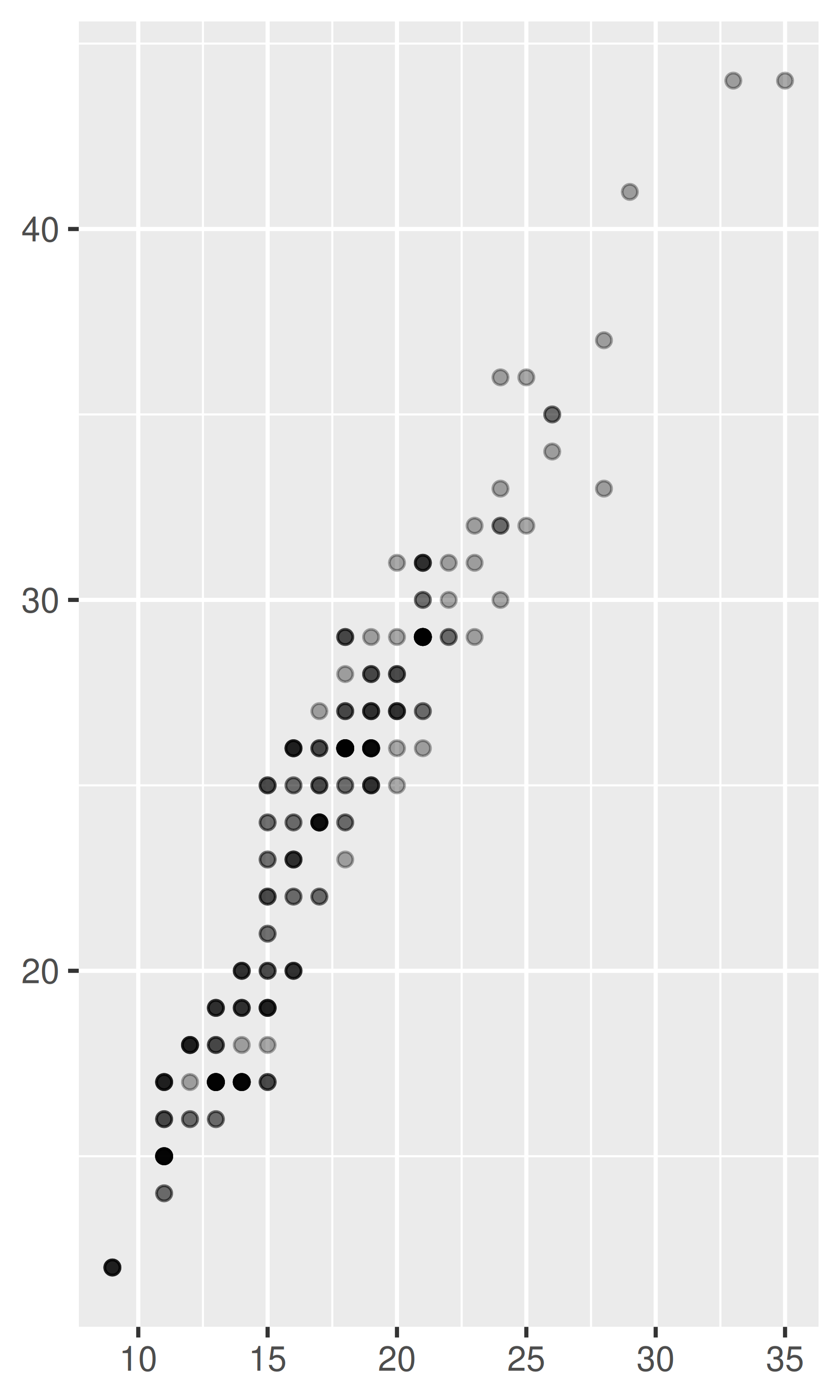
ggplot(mpg, aes(cty, hwy)) +
  geom_point(alpha = 1 / 3) + 
  xlab(NULL) + 
  ylab(NULL)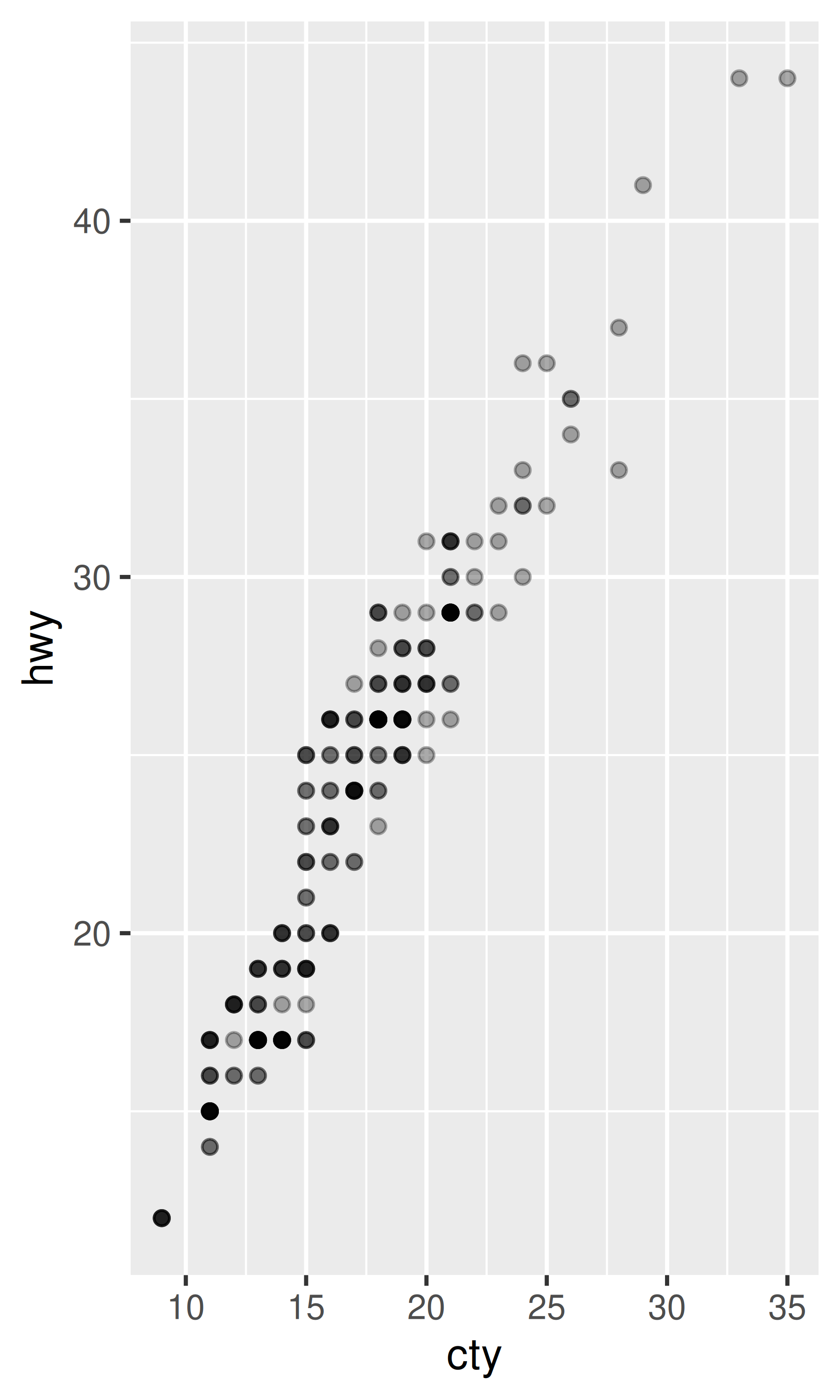

xlim() y ylim() modificar los límites de los ejes:

ggplot(mpg, aes(drv, hwy)) +
  geom_jitter(width = 0.25)

ggplot(mpg, aes(drv, hwy)) +
  geom_jitter(width = 0.25) + 
  xlim("f", "r") + 
  ylim(20, 30)
#> Warning: Removed 138 rows containing missing values or values outside the scale range
#> (`geom_point()`).
  
# For continuous scales, use NA to set only one limit
ggplot(mpg, aes(drv, hwy)) +
  geom_jitter(width = 0.25, na.rm = TRUE) + 
  ylim(NA, 30)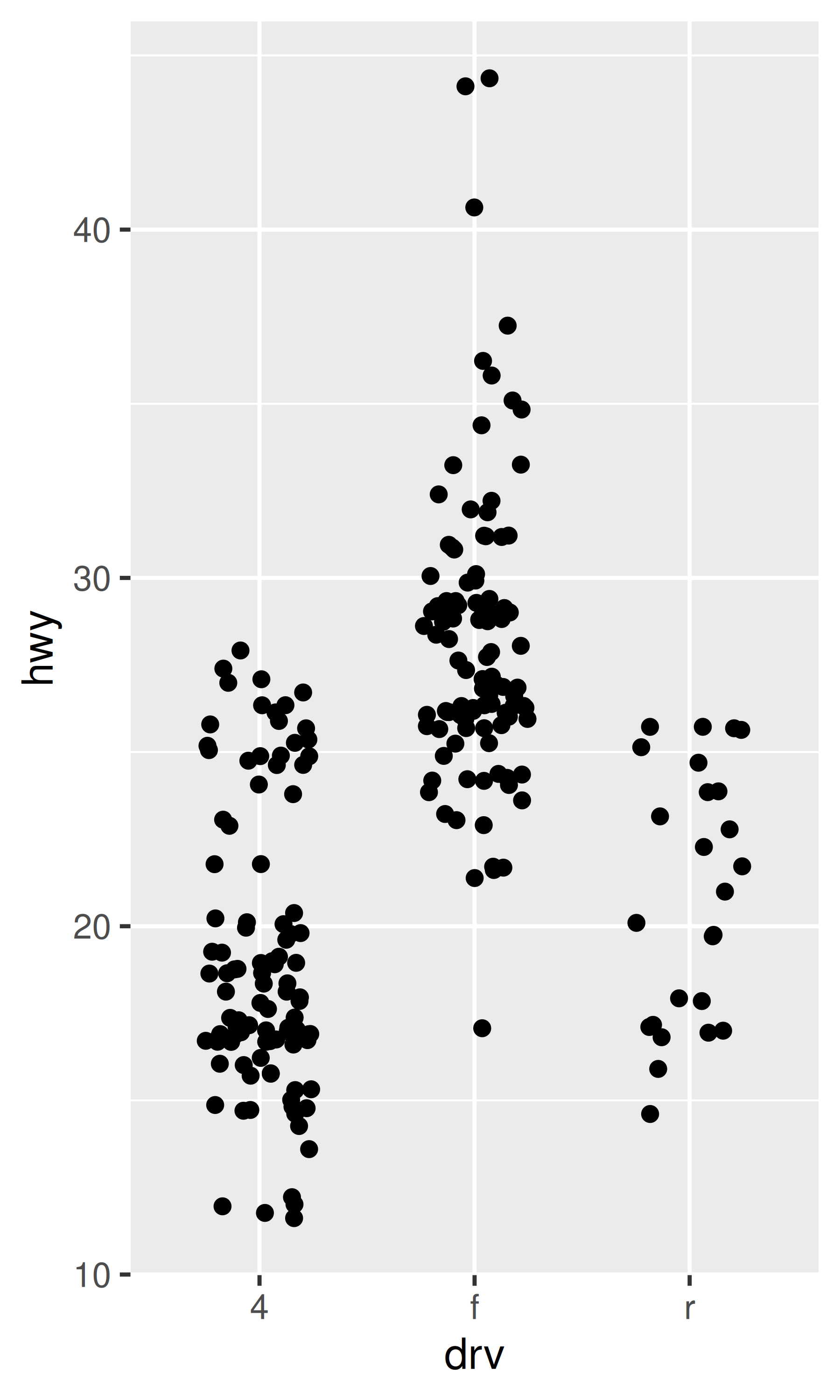

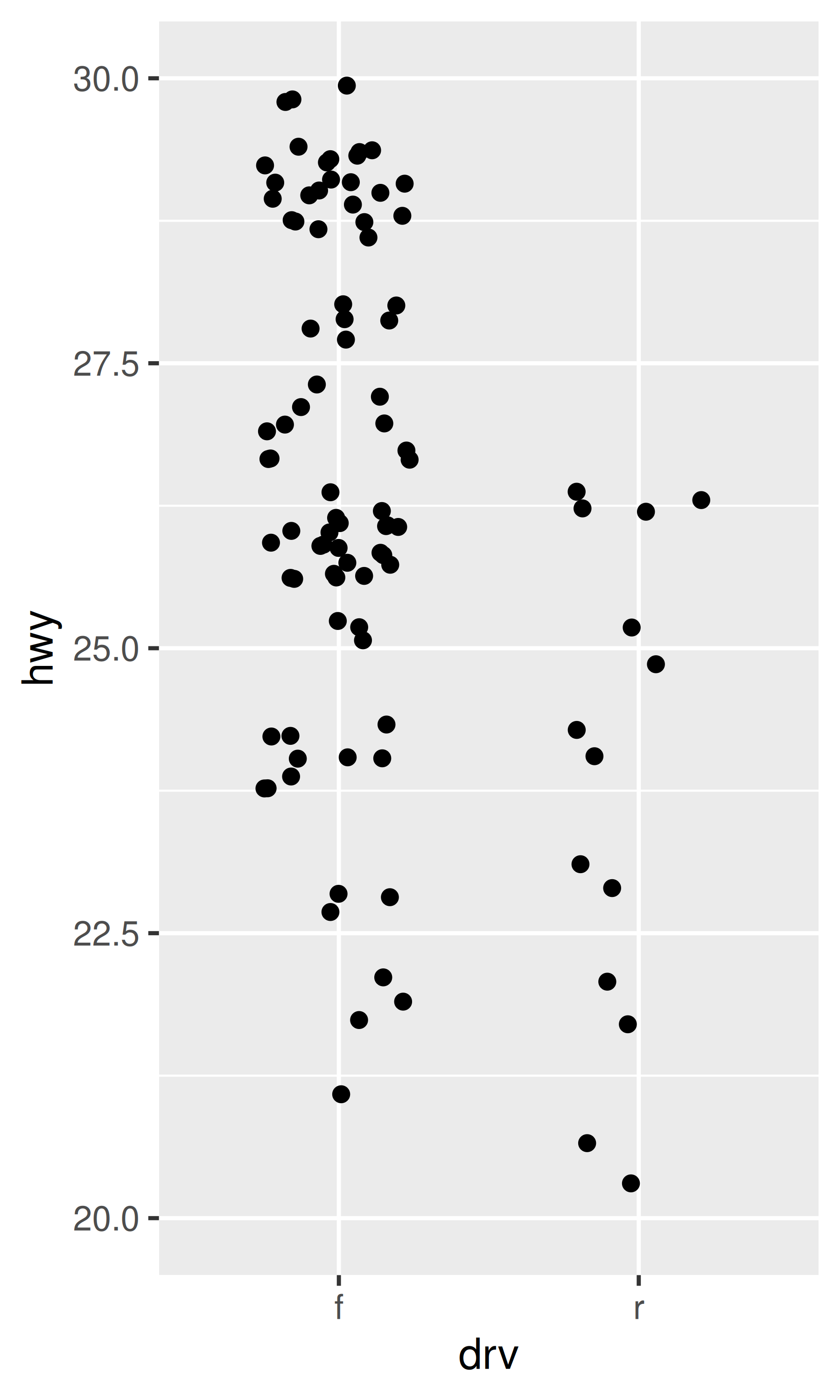
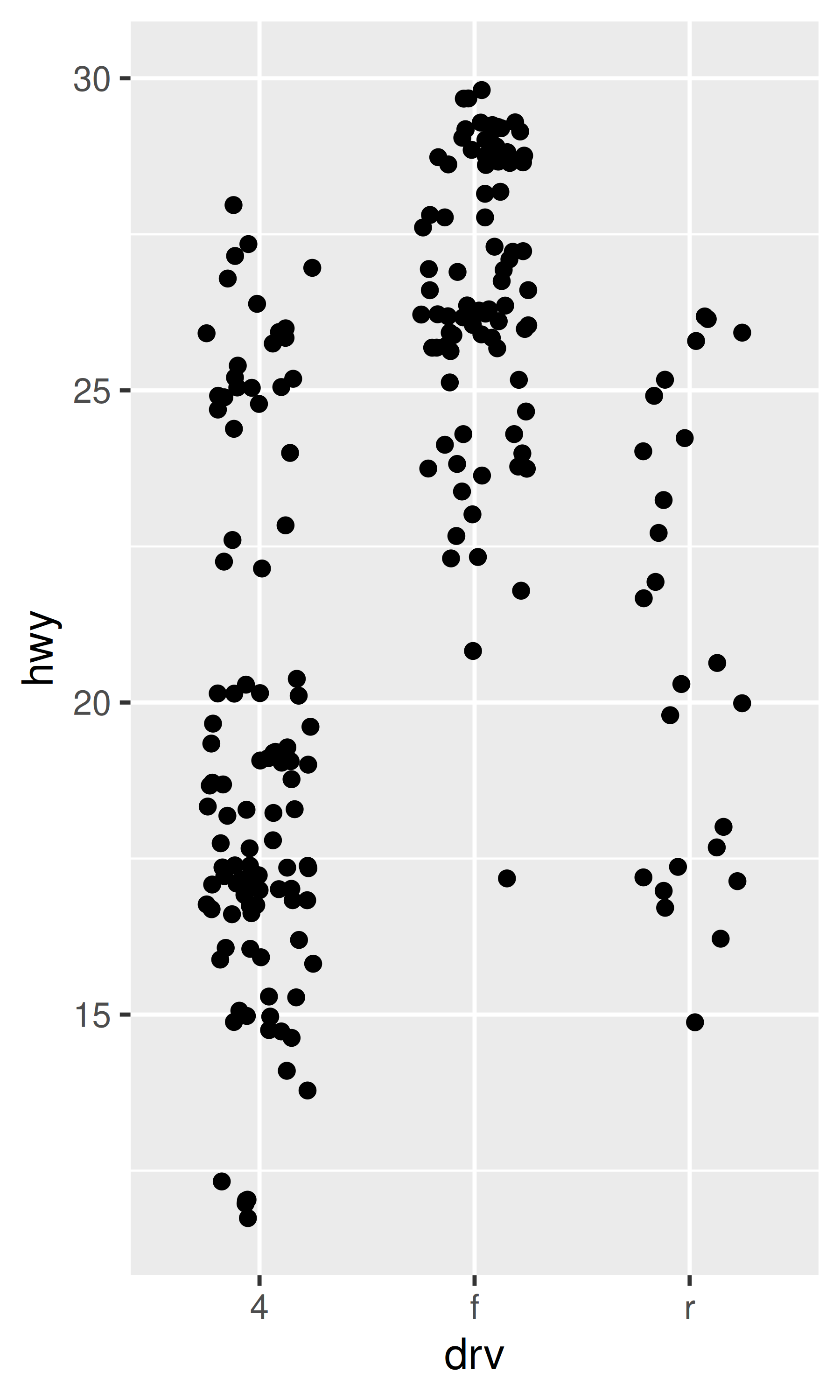
Cambiar los límites de los ejes establece los valores fuera del rango en NA. Puede suprimir la advertencia asociada con na.rm = TRUE, pero tenga cuidado. Si su gráfico calcula estadísticas resumidas (por ejemplo, media muestral), esta conversión a NA ocurre antes de que se calculen las estadísticas resumidas y puede generar resultados no deseados en algunas situaciones.

2.8 Salida

La mayoría de las veces crea un objeto de trazado y lo traza inmediatamente, pero también puede guardar un trazado en una variable y manipularlo:

p <- ggplot(mpg, aes(displ, hwy, colour = factor(cyl))) +
  geom_point()

Una vez que tengas un objeto de gráfica, hay algunas cosas que puedes hacer con él:

Renderizarlo en pantalla con print(). Esto sucede automáticamente cuando se ejecuta de forma interactiva, pero dentro de un bucle o función, necesitarás imprimirlo tú mismo.

::: {.cell}
```
print(p)
```
::: {.cell-output-display} ::: :::

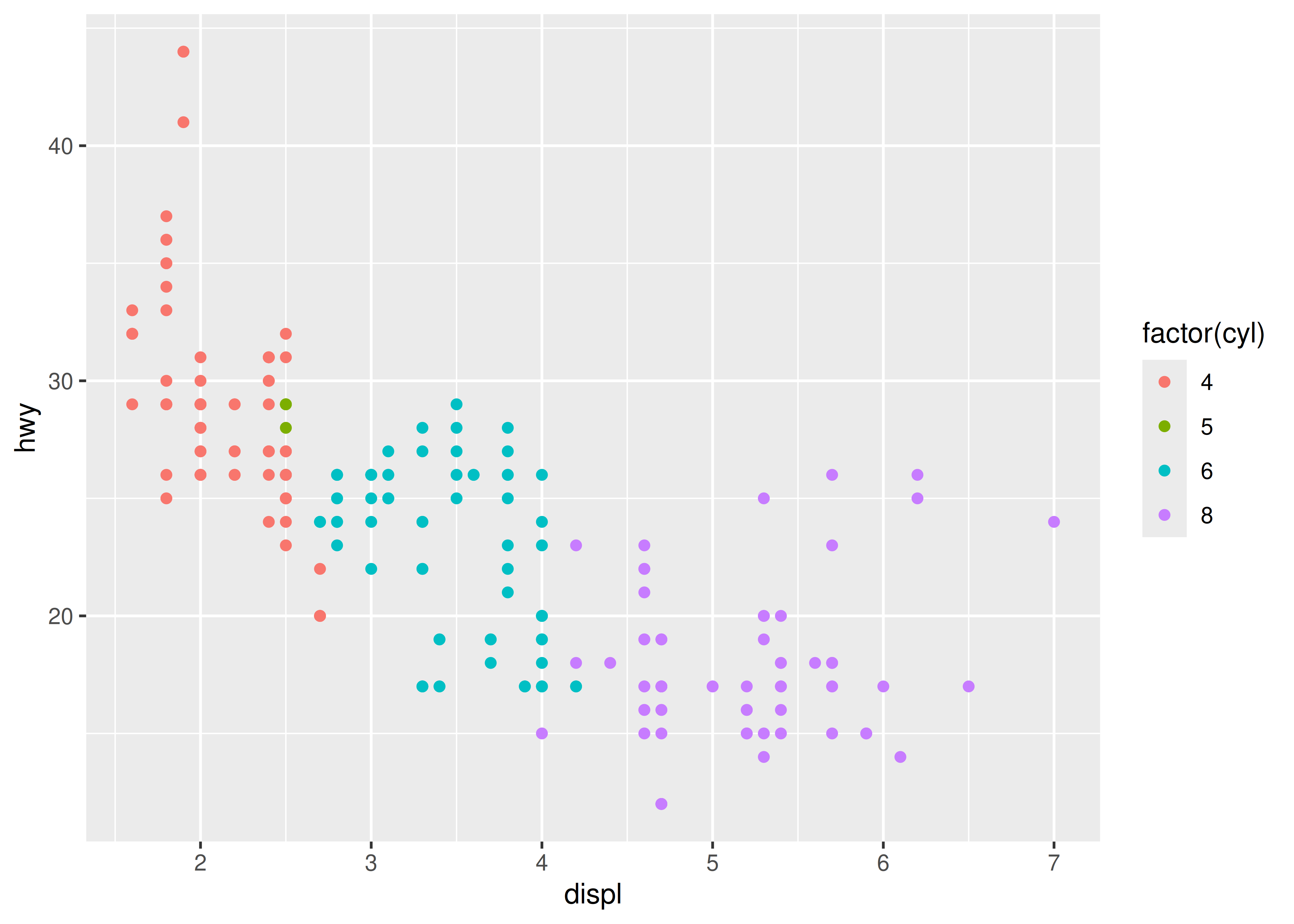Guárdelo en el disco con ggsave(), descrito en Sección 17.5.

# Save png to disk
ggsave("plot.png", p, width = 5, height = 5)

Describe brevemente su estructura con summary().

summary(p)
#> data: manufacturer, model, displ, year, cyl, trans, drv, cty, hwy, fl,
#>   class [234x11]
#> mapping:  x = ~displ, y = ~hwy, colour = ~factor(cyl)
#> faceting: <ggproto object: Class FacetNull, Facet, gg>
#>     compute_layout: function
#>     draw_back: function
#>     draw_front: function
#>     draw_labels: function
#>     draw_panels: function
#>     finish_data: function
#>     init_scales: function
#>     map_data: function
#>     params: list
#>     setup_data: function
#>     setup_params: function
#>     shrink: TRUE
#>     train_scales: function
#>     vars: function
#>     super:  <ggproto object: Class FacetNull, Facet, gg>
#> -----------------------------------
#> geom_point: na.rm = FALSE
#> stat_identity: na.rm = FALSE
#> position_identity

Aprenderá más sobre cómo manipular estos objetos en Capítulo 18.