La Gramática

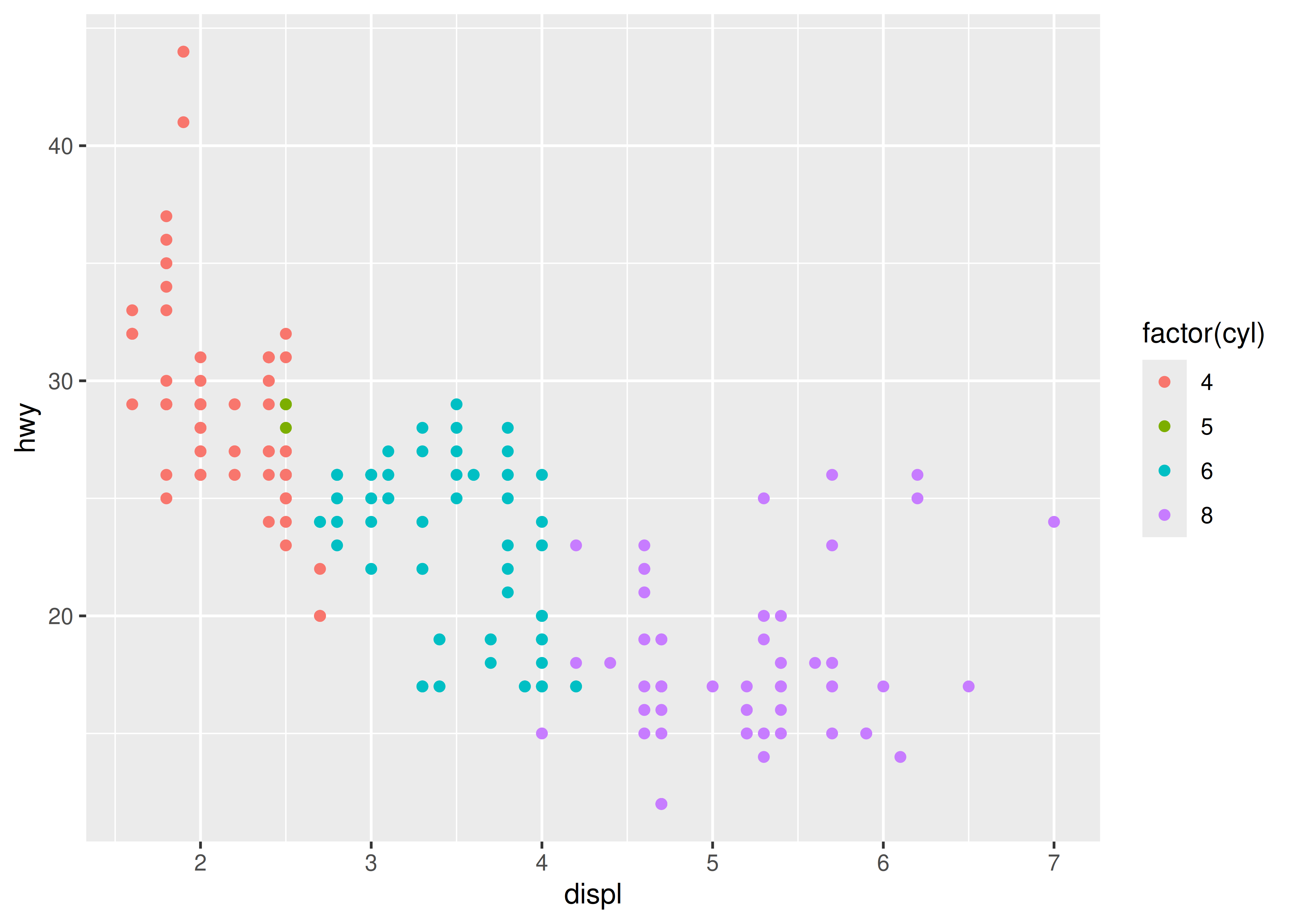
You are reading the work-in-progress third edition of the ggplot2 book. This chapter is currently a dumping ground for ideas, and we don’t recommend reading it.

Para desbloquear todo el poder de ggplot2, necesitarás dominar la gramática subyacente. Al comprender la gramática y cómo encajan sus componentes, puede crear una gama más amplia de visualizaciones, combinar múltiples fuentes de datos y personalizarlas a su gusto.

Este capítulo describe la base teórica de ggplot2: la gramática en capas de gráficos. La gramática en capas se basa en la gramática de gráficos de Wilkinson (Wilkinson 2005), pero agrega una serie de mejoras que la ayudan a ser más expresiva y encajar perfectamente en el entorno R. Las diferencias entre la gramática en capas y la gramática de Wilkinson se describen detalladamente en Wickham (2008). En este capítulo aprenderá un poco sobre cada componente de la gramática y cómo encajan todos. Los siguientes capítulos analizan los componentes con más detalle y brindan más ejemplos de cómo usarlos en la práctica.

La gramática le facilita la actualización iterativa de un gráfico, cambiando una sola característica a la vez. La gramática también es útil porque sugiere los aspectos de alto nivel de una gráfica que pueden cambiarse, brindándole un marco para pensar en los gráficos y, con suerte, acortando la distancia entre la mente y el papel. También fomenta el uso de gráficos personalizados para un problema particular, en lugar de depender de tipos de gráficos específicos.

Este capítulo comienza describiendo en detalle el proceso de dibujar una gráfica simple. Construyendo un diagrama de dispersión comienza con un diagrama de dispersión simple, luego Añadiendo complejidad lo hace más complejo agregando una línea suave y facetas. Mientras trabaja en estos ejemplos, se le presentarán los seis componentes de la gramática, que luego se definen con mayor precisión en Componentes de la gramática en capas..

Construyendo un diagrama de dispersión

¿Cómo se relacionan el tamaño del motor y la economía de combustible? Podríamos crear un diagrama de dispersión de la cilindrada del motor y las mpg en carretera con puntos coloreados según el número de cilindros:

ggplot(mpg, aes(displ, hwy, colour = factor(cyl))) +
  geom_point()

Puedes crear gráficas como esta fácilmente, pero ¿qué sucede debajo de la superficie? ¿Cómo dibuja ggplot2 este gráfico?

Mapeo de la estética a los datos

¿Qué es exactamente un diagrama de dispersión? Has visto muchos antes y probablemente incluso hayas dibujado algunos a mano. Un diagrama de dispersión representa cada observación como un punto, posicionado según el valor de dos variables. Además de una posición horizontal y vertical, cada punto también tiene un tamaño, un color y una forma. Estos atributos se llaman estética y son las propiedades que se pueden percibir en el gráfico. Cada estética se puede asignar a partir de una variable o establecerse en un valor constante. En el gráfico anterior, “displ” se asigna a la posición horizontal, “hwy” a la posición vertical y “cyl” al color. El tamaño y la forma no se asignan, pero permanecen en sus valores predeterminados (constantes).

Una vez que tengamos estas asignaciones, podemos crear un nuevo conjunto de datos que registre esta información:

x	y	colour
1.8	29	4
1.8	29	4
2.0	31	4
2.0	30	4
2.8	26	6
2.8	26	6
3.1	27	6
1.8	26	4

Este nuevo conjunto de datos es el resultado de aplicar las asignaciones estéticas a los datos originales. Podemos crear muchos tipos diferentes de gráficos utilizando estos datos. El diagrama de dispersión utiliza puntos, pero si en su lugar se dibujasen líneas obtendríamos un diagrama de líneas. Si usáramos barras, obtendríamos un diagrama de barras. Ninguno de esos ejemplos tiene sentido para estos datos, pero aún así podríamos dibujarlos (hemos omitido las leyendas para ahorrar espacio):

ggplot(mpg, aes(displ, hwy, colour = factor(cyl))) +
  geom_line() + 
  theme(legend.position = "none")

ggplot(mpg, aes(displ, hwy, colour = factor(cyl))) +
  geom_bar(stat = "identity", position = "identity", fill = NA) + 
  theme(legend.position = "none")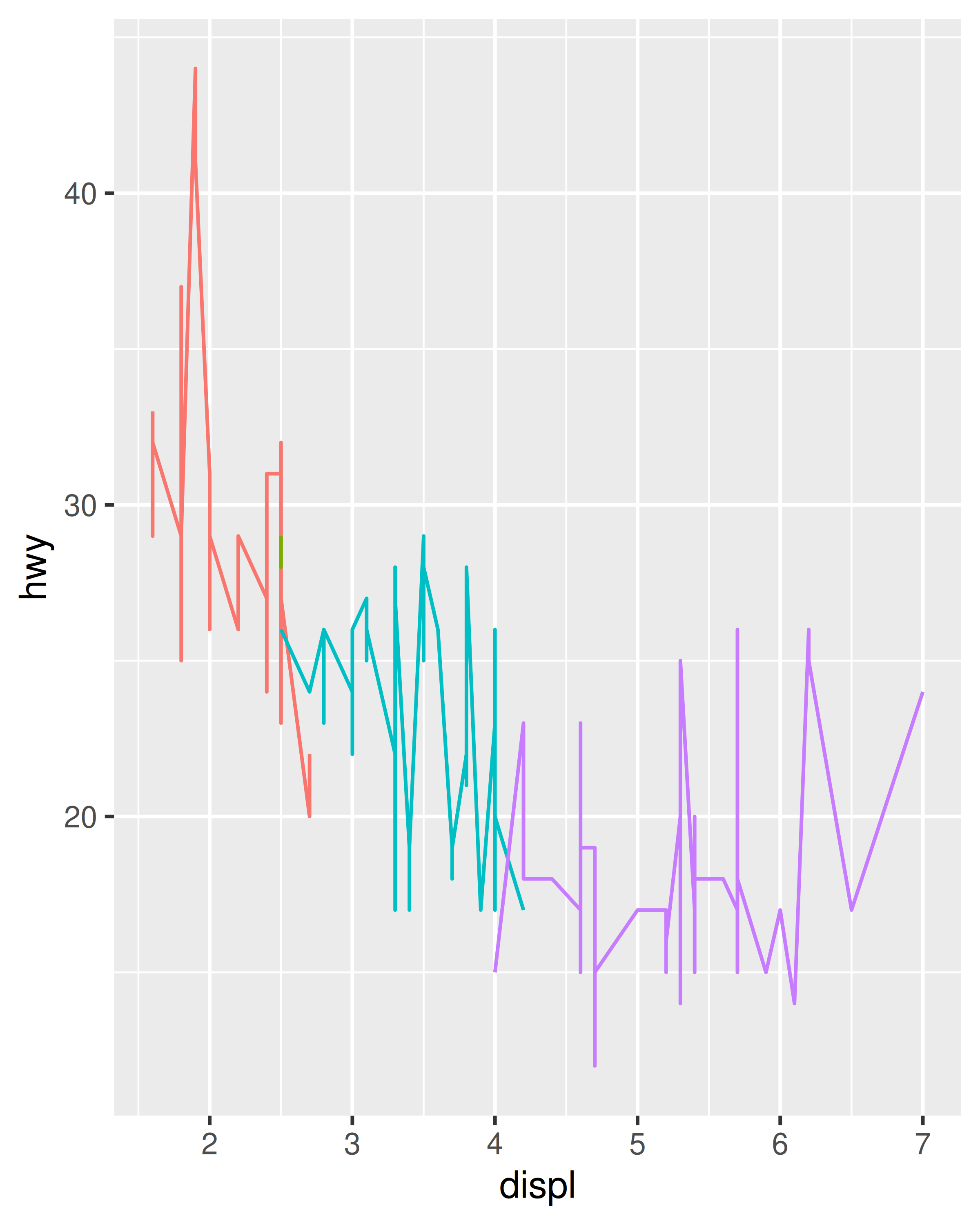

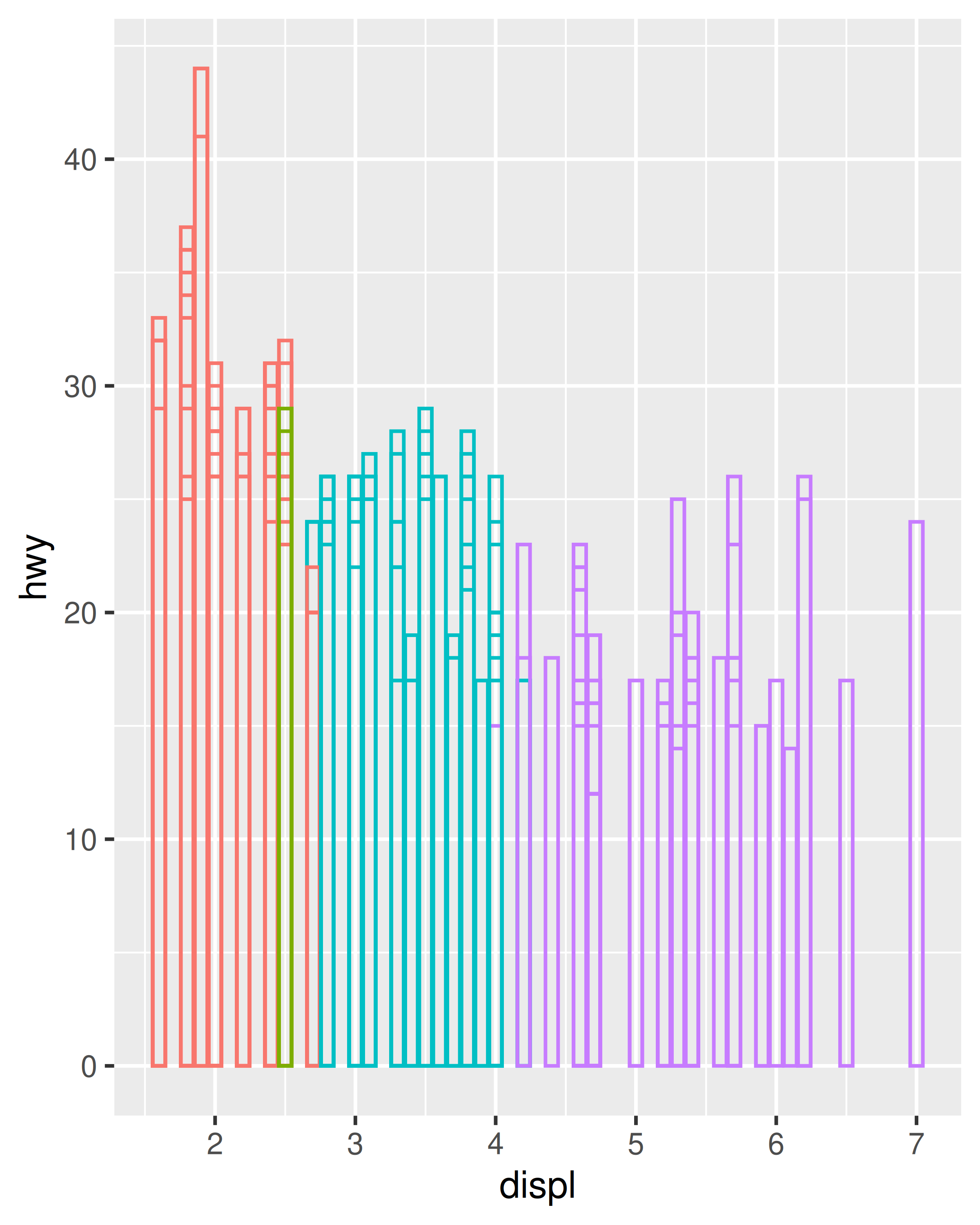
En ggplot, podemos producir muchos gráficos que no tienen sentido, pero que son gramaticalmente válidos. Esto no es diferente al español, donde podemos crear oraciones sin sentido pero gramaticales como la roca enojada ladra como una coma.

Los puntos, las líneas y las barras son ejemplos de objetos geométricos o geoms. Las geomas determinan el “tipo” de la gráfica. Las gráficas que utilizan una sola geom suelen recibir un nombre especial:

Named plot	Geom	Other features
gráfico de dispersión	point
gráfico de burbujas	point	size mapped to a variable
gráfico de barras	bar
diagrama de caja	boxplot
gráfico de línea	line

Las gráficas más complejas con combinaciones de múltiples geoms no tienen un nombre especial y tenemos que describirlas a mano. Por ejemplo, este gráfico superpone una línea de regresión por grupo encima de un diagrama de dispersión:

ggplot(mpg, aes(displ, hwy, colour = factor(cyl))) + 
  geom_point() + 
  geom_smooth(method = "lm")
#> `geom_smooth()` using formula = 'y ~ x'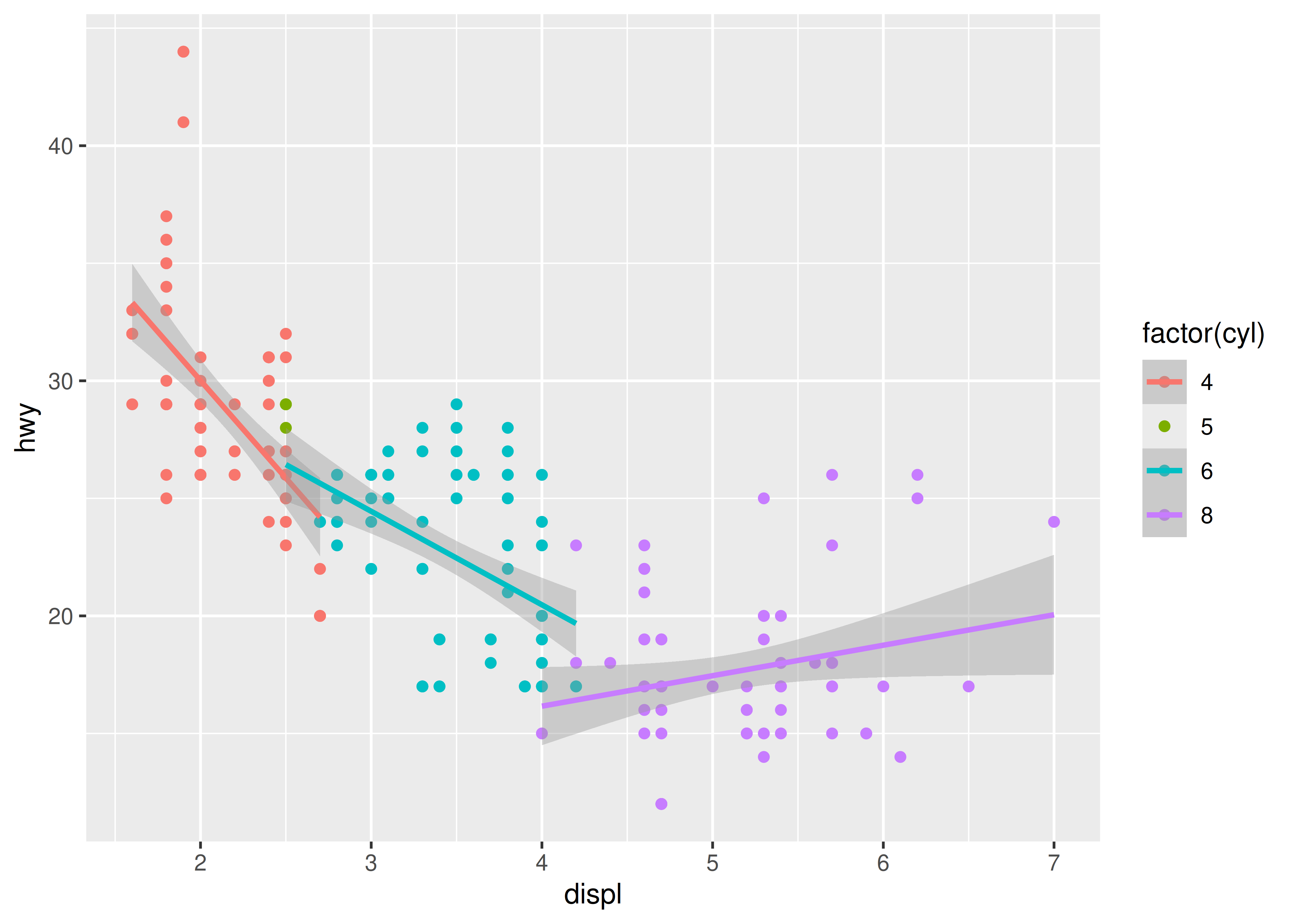

¿Cómo llamarías a esta gráfica? Una vez que haya dominado la gramática, descubrirá que muchas de las gráficas que produzca se adaptan exclusivamente a sus problemas y ya no tendrán nombres especiales.

Escalado

Los valores de la tabla anterior no tienen significado para la computadora. Necesitamos convertirlos de unidades de datos (por ejemplo, litros, millas por galón y número de cilindros) a unidades gráficas (por ejemplo, píxeles y colores) que la computadora pueda mostrar. Este proceso de conversión se llama escalado y se realiza mediante escalas. Ahora que estos valores son significativos para la computadora, es posible que no lo sean para nosotros: los colores se representan mediante una cadena hexadecimal de seis letras, los tamaños mediante un número y las formas mediante un número entero. Estas especificaciones estéticas que son significativas para R se describen en vignette("ggplot2-specs").

En este ejemplo, tenemos tres estéticas que deben escalarse: posición horizontal (x), posición vertical (y) y colour. Escalar la posición es fácil en este ejemplo porque estamos usando las escalas lineales predeterminadas. Solo necesitamos un mapeo lineal desde el rango de datos hasta \([0, 1]\). Usamos \([0, 1]\) en lugar de píxeles exactos porque el sistema de dibujo que usa ggplot2, grid, se encarga de esa conversión final por nosotros. Un paso final determina cómo se combinan las dos posiciones (x e y) para formar la ubicación final en el gráfico. Esto lo realiza el sistema de coordenadas o coord. En la mayoría de los casos, serán coordenadas cartesianas, pero podrían ser coordenadas polares o una proyección esférica utilizada para un mapa.

El proceso de mapeo del color es un poco más complicado, ya que tenemos un resultado no numérico: colores. Sin embargo, se puede considerar que los colores tienen tres componentes, correspondientes a los tres tipos de células que detectan el color en el ojo humano. Estos tres tipos de células dan lugar a un espacio de color tridimensional. Luego, el escalado implica asignar los valores de datos a puntos en este espacio. Hay muchas formas de hacer esto, pero aquí, dado que cyl es una variable categórica, asignamos valores a tonos espaciados uniformemente en la rueda de colores, como se muestra en la siguiente figura. Se utiliza un mapeo diferente cuando la variable es continua.

Una rueda de colores que ilustra la elección de cinco colores equiespaciados. Esta es la escala predeterminada para variables discretas.

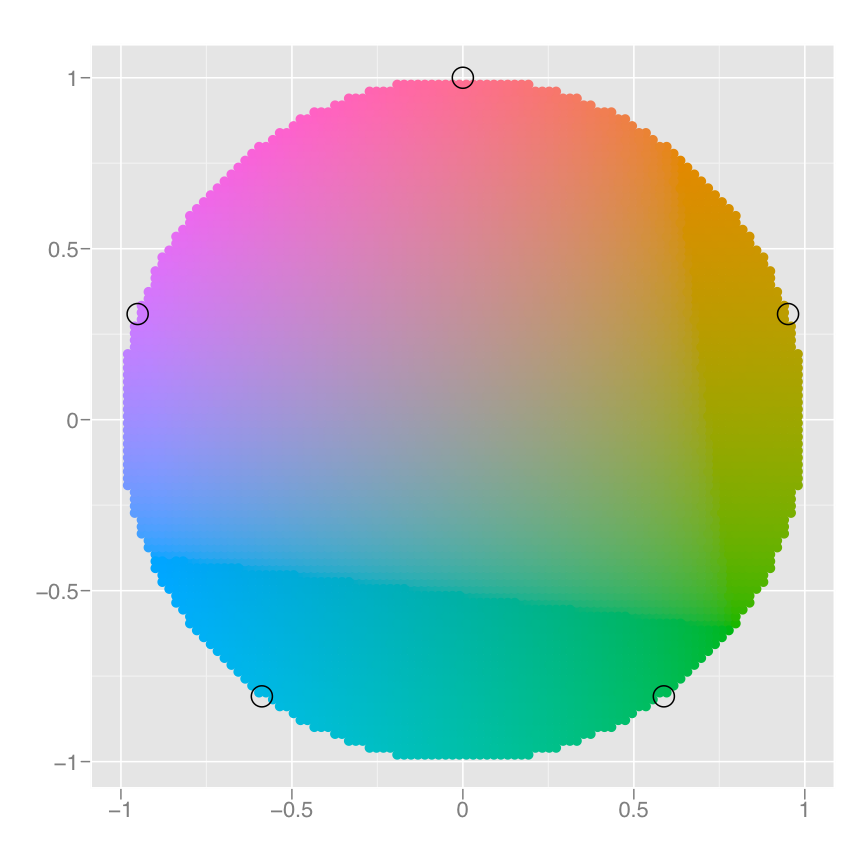
El resultado de estas conversiones se encuentra a continuación. Además de la estética que se ha asignado a variables, también incluimos estéticas que son constantes. Los necesitamos para que la estética de cada punto esté completamente especificada y R pueda dibujar la gráfica. Los puntos serán círculos rellenos (forma 19 en R) con un diámetro de 1 mm:

x	y	colour	size	shape
0.037	0.531	#F8766D	1	19
0.037	0.531	#F8766D	1	19
0.074	0.594	#F8766D	1	19
0.074	0.562	#F8766D	1	19
0.222	0.438	#00BFC4	1	19
0.222	0.438	#00BFC4	1	19
0.278	0.469	#00BFC4	1	19
0.037	0.438	#F8766D	1	19

Finalmente, necesitamos representar estos datos para crear los objetos gráficos que se muestran en la pantalla. Para crear un gráfico completo necesitamos combinar objetos gráficos de tres fuentes: los datos, representados por el punto geom; las escalas y sistema de coordenadas, que generan ejes y leyendas para que podamos leer valores del gráfico; y anotaciones de la gráfica, como el fondo y el título de la gráfica.

Añadiendo complejidad

Con un ejemplo simple en nuestro haber, veamos ahora este ejemplo un poco más complicado:

ggplot(mpg, aes(displ, hwy)) + 
  geom_point() +
  geom_smooth() + 
  facet_wrap(~year)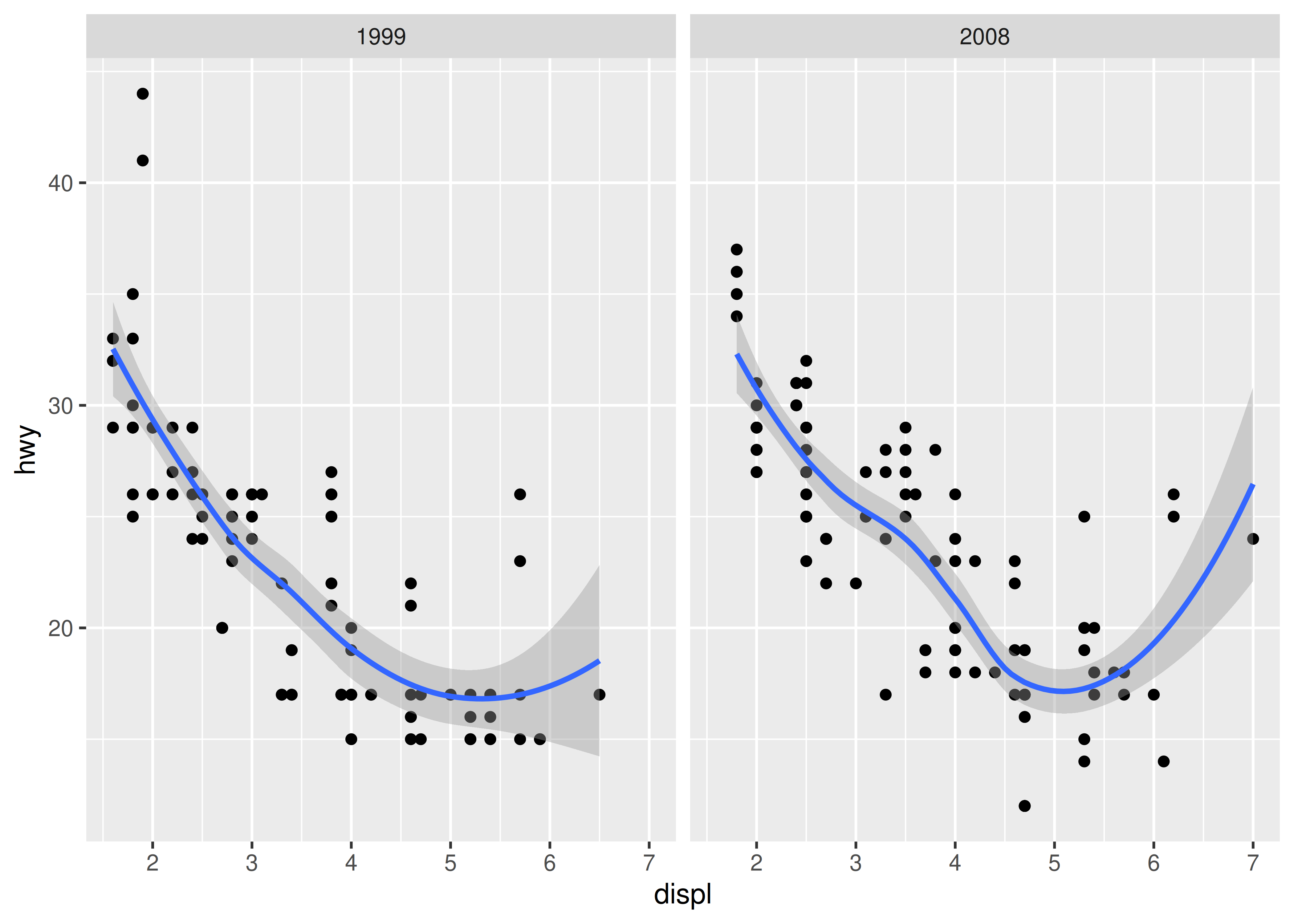

Esta gráfica agrega tres nuevos componentes a la mezcla: facetas, múltiples capas y estadísticas. Las facetas y capas amplían la estructura de datos descrita anteriormente: cada panel de facetas en cada capa tiene su propio conjunto de datos. Puedes pensar en esto como una matriz tridimensional: los paneles de las facetas forman una cuadrícula bidimensional y las capas se extienden hacia arriba en la tercera dimensión. En este caso, los datos de las capas son los mismos, pero en general podemos trazar diferentes conjuntos de datos en diferentes capas.

La capa suave es diferente de la capa de puntos porque no muestra los datos sin procesar, sino que muestra una transformación estadística de los datos. Específicamente, la capa suave se ajusta a una línea suave que pasa por el centro de los datos. Esto requiere un paso adicional en el proceso descrito anteriormente: después de asignar los datos a la estética, los datos se pasan a una transformación estadística, o stat, que manipula los datos de alguna manera útil. En este ejemplo, la estadística ajusta los datos de manera más suave y luego devuelve predicciones desde puntos espaciados uniformemente dentro del rango de los datos. Otras estadísticas útiles incluyen agrupamiento 1 y 2D, medias de grupo, regresión por cuantiles y contorno.

Además de agregar un paso adicional para resumir los datos, también necesitamos algunos pasos adicionales cuando lleguemos a las escalas. Esto se debe a que ahora tenemos múltiples conjuntos de datos (para las diferentes facetas y capas) y debemos asegurarnos de que las escalas sean las mismas en todos ellos. En realidad, el escalamiento se produce en tres partes: transformación, capacitación y mapeo. No hemos mencionado la transformación antes, pero probablemente la hayas visto antes en gráficos log-log. En un gráfico log-log, los valores de los datos no se asignan linealmente a su posición en el gráfico, sino que primero se transforman logarítmicamente.

• La transformación de escala ocurre antes de la transformación estadística, de modo que las estadísticas se calculan sobre los datos transformados a escala. Esto garantiza que una gráfica de \(\log(x)\) frente a \(\log(y)\) en escalas lineales se vea igual que \(x\) frente a \(y\) en escalas logarítmicas. Hay muchas transformaciones diferentes que se pueden utilizar, incluida la extracción de raíces cuadradas, logaritmos y recíprocos. Consulte 10  Escalas de posición y ejes. para obtener más detalles.

• Una vez calculadas las estadísticas, cada escala se entrena en cada conjunto de datos de todas las capas y facetas. La operación de entrenamiento combina los rangos de los conjuntos de datos individuales para obtener el rango de los datos completos. Sin este paso, las escalas sólo podrían tener sentido localmente y no podríamos superponer diferentes capas porque sus posiciones no se alinearían. A veces queremos variar las escalas de posición entre facetas (pero nunca entre capas), y esto se describe con más detalle en Control de escalas.

• Finalmente, las escalas asignan los valores de los datos a valores estéticos. Esta es una operación local: las variables en cada conjunto de datos se asignan a sus valores estéticos, lo que produce un nuevo conjunto de datos que luego las geoms pueden representar.

La siguiente figura ilustra esquemáticamente el proceso completo.

Descripción esquemática del proceso de generación de gráficas. Cada cuadrado representa una capa y este esquema representa una gráfica con tres capas y tres paneles. Todos los pasos funcionan transformando marcos de datos individuales, excepto las escalas de entrenamiento, que no afectan el marco de datos y operan en todos los conjuntos de datos simultáneamente.

Componentes de la gramática en capas.

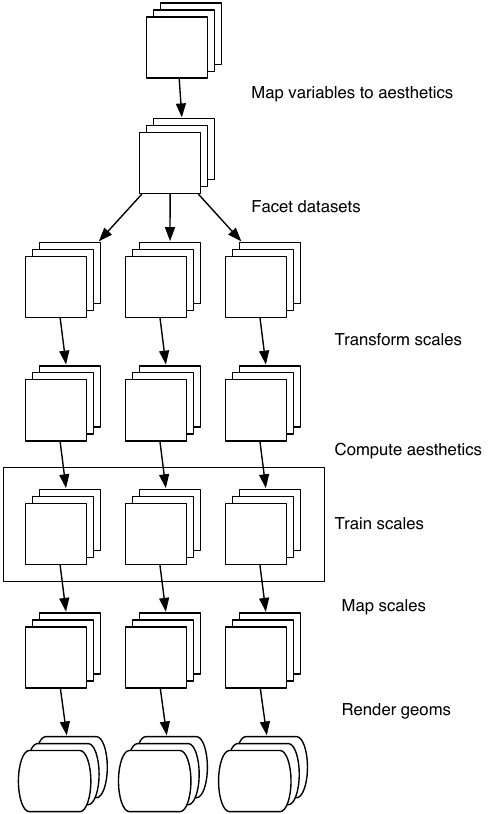
En los ejemplos anteriores, hemos visto algunos de los componentes que componen una gráfica: datos y asignaciones estéticas, objetos geométricos (geoms), transformaciones estadísticas (stats), escalas y facetas. También hemos tocado el sistema de coordenadas. Una cosa que no mencionamos es el ajuste de posición, que se ocupa de la superposición de objetos gráficos. Juntos, los datos, asignaciones, estadísticas, geom y ajustes de posición forman una capa. Un gráfico puede tener varias capas, como en el ejemplo en el que superpusimos una línea suavizada en un diagrama de dispersión. En conjunto, la gramática en capas define una gráfica como la combinación de:

• Un conjunto de datos predeterminado y un conjunto de asignaciones de variables a estética.

• Una o más capas, cada una compuesta por un objeto geométrico, una transformación estadística, un ajuste de posición y, opcionalmente, un conjunto de datos y mapeos estéticos.

• Una escala para cada mapeo estético.

• Un sistema de coordenadas.

• La especificación de facetado.

Las siguientes secciones describen cada uno de los componentes de nivel superior con mayor precisión y le indican las partes del libro donde están documentados.

Capas

Las capas son las encargadas de crear los objetos que percibimos en la gráfica. Una capa se compone de cinco partes:

1. Datos
2. Mapeos estéticos.
3. Una transformación estadística (stat).
4. Un objeto geométrico (geom).
5. Un ajuste de posición.

Las propiedades de una capa se describen en 13  Construya una gráfica capa por capa y sus usos para la visualización de datos se describen en 3  Geomas individuales a 8  Anotaciones.

Escalas

Una escala controla el mapeo de los datos a los atributos estéticos, y necesitamos una escala para cada estética utilizada en una gráfica. Cada escala opera en todos los datos del gráfico, lo que garantiza un mapeo consistente desde los datos hasta la estética. Algunos ejemplos se muestran a continuación.

Ejemplos de leyendas de cuatro escalas diferentes. De izquierda a derecha: variable continua asignada a tamaño y color, variable discreta asignada a forma y color. El orden de las escalas parece al revés, pero coincide con el etiquetado del eje \(y\): los valores pequeños aparecen en la parte inferior.

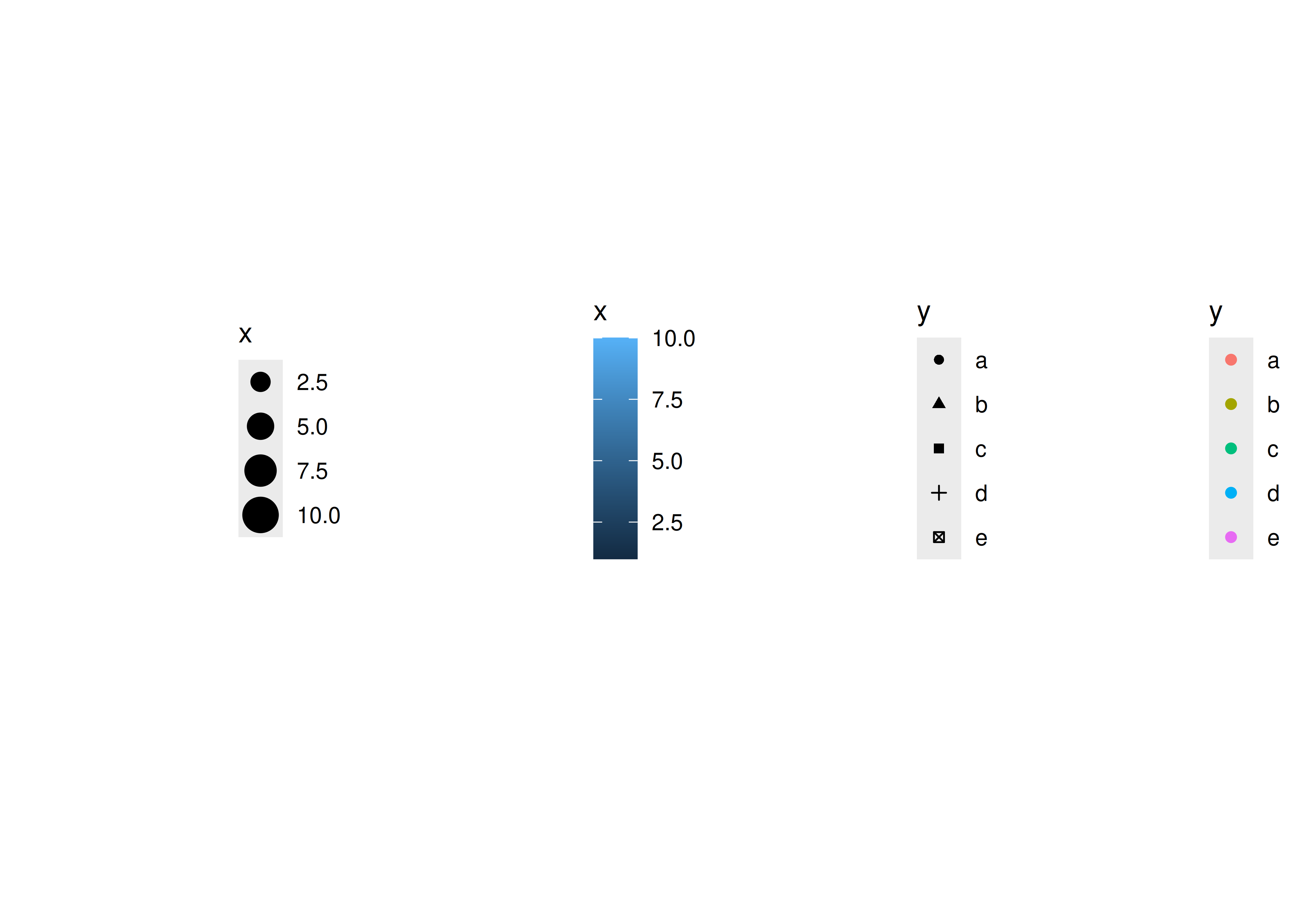
Una escala es una función y su inversa, junto con un conjunto de parámetros. Por ejemplo, la escala de gradiente de color asigna un segmento de la línea real a una ruta a través de un espacio de color. Los parámetros de la función definen si la ruta es lineal o curva, qué espacio de color usar (por ejemplo, LUV o RGB) y los colores al principio y al final.

La función inversa se utiliza para dibujar una guía para que pueda leer los valores del gráfico. Las guías son ejes (para escalas de posición) o leyendas (para todo lo demás). La mayoría de las asignaciones tienen una inversa única (es decir, la función de asignación es uno a uno), pero muchas no la tienen. Un inverso único permite recuperar los datos originales, pero esto no siempre es deseable si queremos centrar la atención en un solo aspecto.

Para más detalles, ver 11  Escalas de colores y leyendas..

Sistema coordinado

Un sistema de coordenadas, o coord para abreviar, asigna la posición de los objetos al plano del gráfico. La posición a menudo se especifica mediante dos coordenadas \((x, y)\), pero potencialmente podrían ser tres o más (aunque esto no está implementado en ggplot2). El sistema de coordenadas cartesiano es el sistema de coordenadas más común para dos dimensiones, mientras que las coordenadas polares y varias proyecciones cartográficas se utilizan con menos frecuencia.

Los sistemas de coordenadas afectan a todas las variables de posición simultáneamente y se diferencian de las escalas en que también cambian la apariencia de los objetos geométricos. Por ejemplo, en coordenadas polares, las geomas de barra parecen segmentos de un círculo. Además, el escalado se realiza antes de la transformación estadística, mientras que las transformaciones de coordenadas se producen después. Las consecuencias de esto se muestran en Sistemas de coordenadas no lineales.

Los sistemas de coordenadas controlan cómo se dibujan los ejes y las líneas de la cuadrícula. La siguiente figura ilustra tres tipos diferentes de sistemas de coordenadas: cartesiano, semilogarítmico y polar. Hay muy pocos consejos disponibles para dibujarlos para sistemas de coordenadas no cartesianas, por lo que se necesita mucho trabajo por hacer para producir resultados pulidos. Consulte 15  Sistemas coordinados para obtener más detalles.

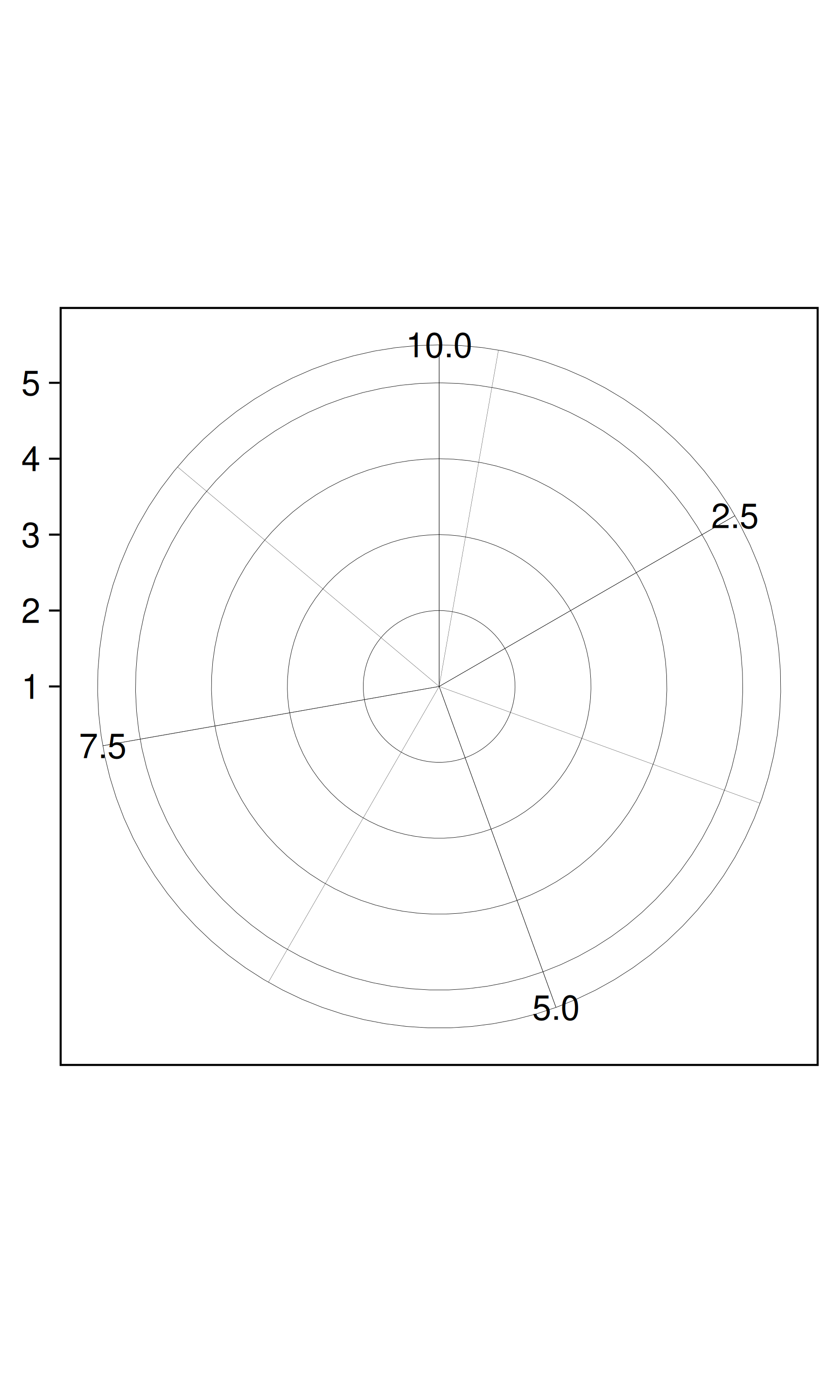
El sistema de coordenadas polares ilustra las dificultades asociadas con las coordenadas no cartesianas: es difícil dibujar bien los ejes.

Facetado

También hay otra cosa que resulta suficientemente útil como para incluirla en nuestro marco general: el facetado, un caso general de gráficas condicionadas o enrejadas. Esto facilita la creación de pequeños múltiplos, cada uno de los cuales muestra un subconjunto diferente de todo el conjunto de datos. Esta es una herramienta poderosa para investigar si los patrones se mantienen en todas las condiciones. La especificación de facetado describe qué variables deben usarse para dividir los datos y si las escalas de posición deben ser libres o restringidas. El facetado se describe en Ajustes de posición.

Ejercicios

1. Una de las mejores formas de comprender cómo funciona la gramática es aplicarla al análisis de gráficos existentes. Para cada uno de los gráficos enumerados a continuación, escriba los componentes del gráfico. No te preocupes si no sabes cómo se llaman las funciones correspondientes en ggplot2 (¡o si siquiera existen!), enfócate en registrar los elementos clave de una gráfica para poder comunicárselo a otra persona.

   1. “La marcha de Napoleón” de Charles John Minard: http://www.datavis.ca/gallery/re-minard.php

   2. “Donde el calor y el trueno acertaron”, por Jeremy White, Joe Ward y Matthew Ericson en The New York Times. http://nyti.ms/1duzTvY

   3. “Viajes de alquiler de bicicletas en Londres”, por James Cheshire. http://bit.ly/1S2cyRy

   4. Las visualizaciones de datos favoritas del Pew Research Center de 2014: http://pewrsr.ch/1KZSSN6

   5. “Los Tony nunca han estado tan dominados por las mujeres”, por Joanna Kao en FiveThirtyEight: http://53eig.ht/1cJRCyG

   6. “En Climbing Income Ladder, la ubicación importa”, de Mike Bostock, Shan Carter, Amanda Cox, Matthew Ericson, Josh Keller, Alicia Parlapiano, Kevin Quealy y Josh Williams en el New York Times: http://nyti.ms/1S2dJQT

   7. “Diseccionando un tráiler: las partes de la película que hacen el corte”, por Shan Carter, Amanda Cox y Mike Bostock en el New York Times: http://nyti.ms/1KTJQOE

Wickham, Hadley. 2008. «Practical tools for exploring data and models». Tesis doctoral, Iowa State University. http://had.co.nz/thesis.

Wilkinson, Leland. 2005. The Grammar of Graphics. 2nd ed. Statistics y Computing. Springer.