6  Mapas

You are reading the work-in-progress third edition of the ggplot2 book. This chapter should be readable but is currently undergoing final polishing.

Trazar datos geoespaciales es una tarea de visualización común y que requiere herramientas especializadas. Normalmente, el problema se puede descomponer en dos problemas: utilizar una fuente de datos para dibujar un mapa y agregar metadatos de otra fuente de información al mapa. Este capítulo le ayudará a abordar ambos problemas. Hemos estructurado el capítulo de la siguiente manera: Sección 6.1 describe una forma sencilla de dibujar mapas usando geom_polygon(), seguida en Sección 6.2 por un enfoque moderno de “características simples” (sf) usando geom_sf(). A continuación, Sección 6.3 y Sección 6.4 analizan cómo trabajar con proyecciones de mapas y la estructura de datos sf subyacente. Finalmente, Sección 6.5 analiza cómo dibujar mapas basados en datos ráster.

6.1 Mapas de polígonos

Quizás el método más sencillo para dibujar mapas sea utilizar geom_polygon() para dibujar límites para diferentes regiones. Para este ejemplo tomamos datos del paquete de mapas usando ggplot2::map_data(). El paquete de mapas no es particularmente preciso ni está actualizado, pero está integrado en R, por lo que es un lugar fácil para comenzar. Aquí hay un conjunto de datos que especifica los límites del condado de Michigan:

mi_counties <- map_data("county", "michigan") %>% 
  select(lon = long, lat, group, id = subregion)
head(mi_counties)
#>     lon  lat group     id
#> 1 -83.9 44.9     1 alcona
#> 2 -83.4 44.9     1 alcona
#> 3 -83.4 44.9     1 alcona
#> 4 -83.3 44.8     1 alcona
#> 5 -83.3 44.8     1 alcona
#> 6 -83.3 44.8     1 alcona

En este conjunto de datos tenemos cuatro variables: lat y long especifican la latitud y longitud de un vértice (es decir, una esquina del polígono), id especifica el nombre de una región y group proporciona un valor único. identificador de áreas contiguas dentro de una región (por ejemplo, si una región constaba de varias islas). Para tener una mejor idea de lo que contienen los datos, podemos trazar mi_counties usando geom_point(), como se muestra en el panel izquierdo a continuación. En este gráfico, cada fila del marco de datos se traza como un único punto, lo que produce un diagrama de dispersión que muestra las esquinas de cada condado. Para convertir este diagrama de dispersión en un mapa, usamos geom_polygon(), que dibuja cada condado como un polígono distinto. Esto se ilustra en el panel derecho a continuación.

ggplot(mi_counties, aes(lon, lat)) + 
  geom_point(size = .25, show.legend = FALSE) +
  coord_quickmap()

ggplot(mi_counties, aes(lon, lat, group = group)) +
  geom_polygon(fill = "white", colour = "grey50") + 
  coord_quickmap()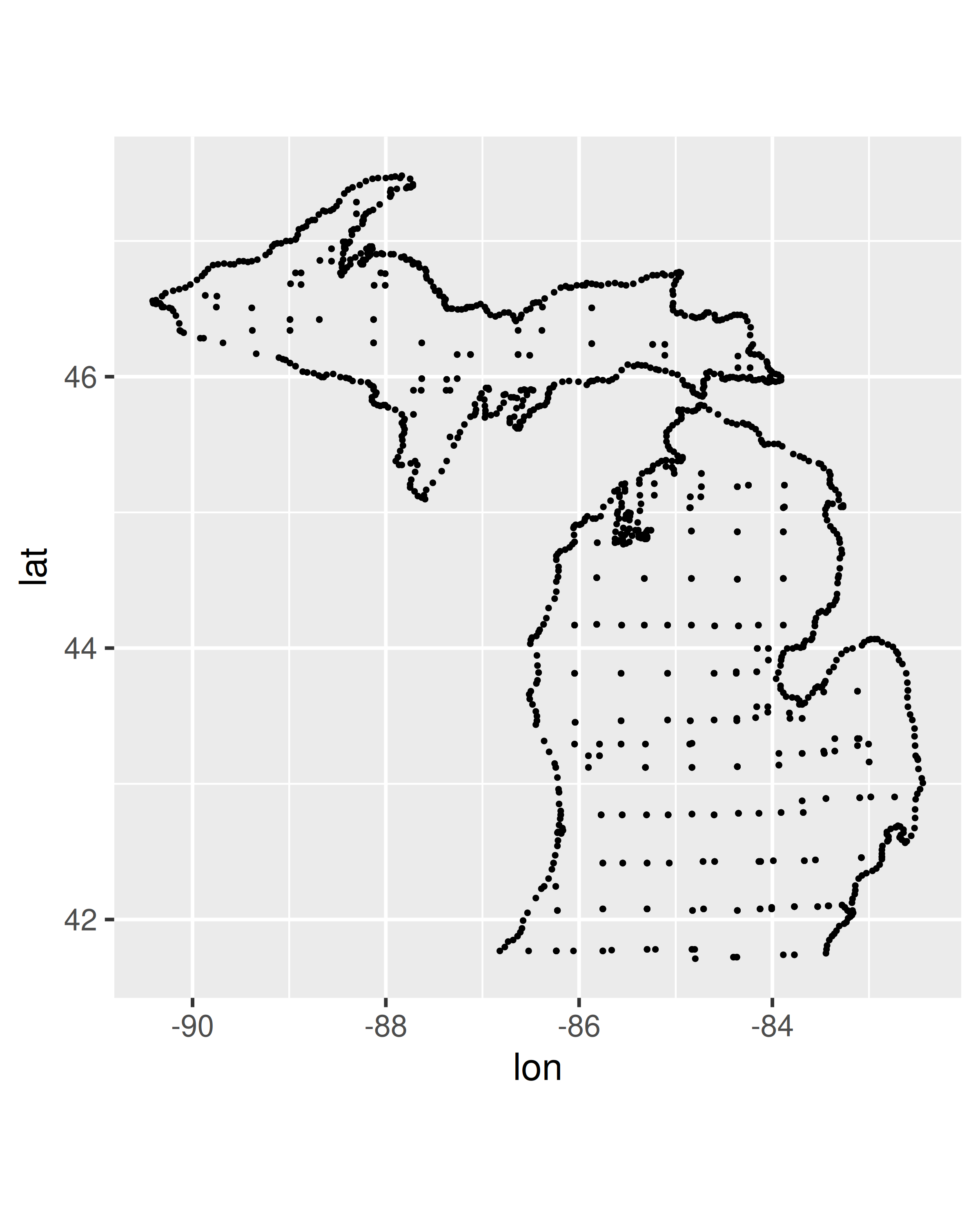

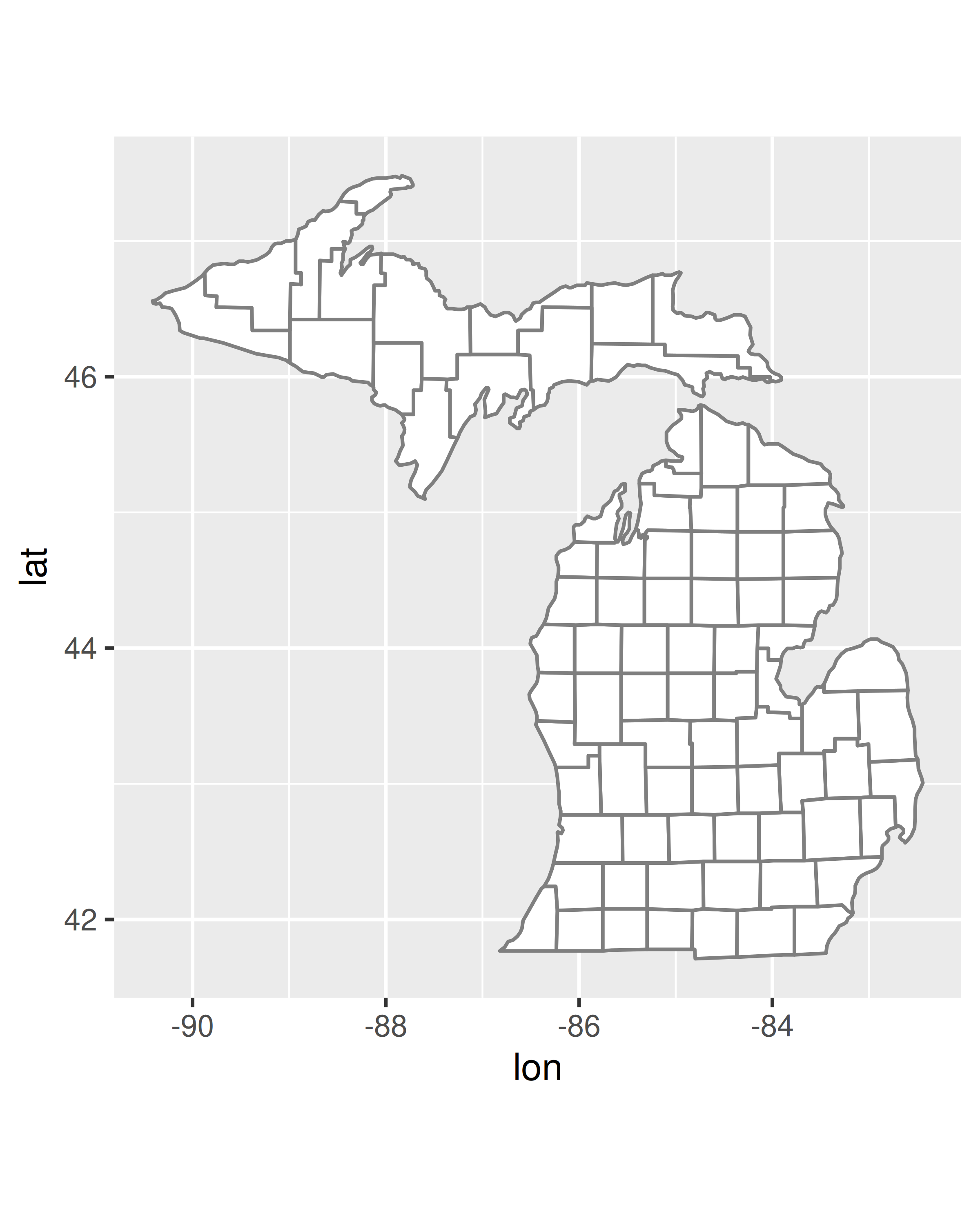
En ambos gráficos usamos coord_quickmap() para ajustar los ejes y garantizar que la longitud y la latitud se representen en la misma escala. Capítulo 15 analiza los sistemas de coordenadas en ggplot2 en términos más generales, pero como veremos a continuación, los datos geoespaciales a menudo requieren un enfoque más exigente. Por esta razón, ggplot2 proporciona geom_sf() y coord_sf() para manejar datos espaciales especificados en formato de características simples.

6.2 Mapas de características simples

El enfoque descrito anteriormente tiene algunas limitaciones, entre las que destaca el hecho de que el formato de datos simple “longitud-latitud” no se utiliza normalmente en la cartografía del mundo real. Los datos vectoriales para mapas normalmente se codifican utilizando el estándar de “características simples” producido por el Open Geospatial Consortium. El paquete sf (Pebesma 2018) desarrollado por Edzer Pebesma https://github.com/r-spatial/sf proporciona un excelente conjunto de herramientas para trabajar con dichos datos y las funciones geom_sf() y coord_sf() en ggplot2 están diseñados para funcionar junto con el paquete sf.

Para presentar estas funciones, nos basamos en el paquete ozmaps de Michael Sumner https://github.com/mdsumner/ozmaps/ que proporciona mapas de las fronteras estatales de Australia, áreas de gobierno local, límites electorales, etc. (Sumner 2019) . Para ilustrar cómo se ve un conjunto de datos sf, importamos un conjunto de datos que representa las fronteras de los estados y territorios australianos:

library(ozmaps)
library(sf)
#> Linking to GEOS 3.12.1, GDAL 3.8.4, PROJ 9.4.0; sf_use_s2() is TRUE

oz_states <- ozmaps::ozmap_states
oz_states
#> Simple feature collection with 9 features and 1 field
#> Geometry type: MULTIPOLYGON
#> Dimension:     XY
#> Bounding box:  xmin: 106 ymin: -43.6 xmax: 168 ymax: -9.23
#> Geodetic CRS:  GDA94
#> # A tibble: 9 × 2
#>   NAME                                                                  geometry
#> * <chr>                                                       <MULTIPOLYGON [°]>
#> 1 New South Wales   (((151 -35.1, 151 -35.1, 151 -35.1, 151 -35.1, 151 -35.2, 1…
#> 2 Victoria          (((147 -38.7, 147 -38.7, 147 -38.7, 147 -38.7, 147 -38.7)),…
#> 3 Queensland        (((149 -20.3, 149 -20.4, 149 -20.4, 149 -20.3)), ((149 -20.…
#> 4 South Australia   (((137 -34.5, 137 -34.5, 137 -34.5, 137 -34.5, 137 -34.5, 1…
#> 5 Western Australia (((126 -14, 126 -14, 126 -14, 126 -14, 126 -14)), ((124 -16…
#> 6 Tasmania          (((148 -40.3, 148 -40.3, 148 -40.3, 148 -40.3)), ((147 -39.…
#> # ℹ 3 more rows

Este resultado muestra algunos de los metadatos asociados con los datos (que se analizan momentáneamente) y nos dice que los datos son esencialmente un tibble con 9 filas y 2 columnas. Una ventaja de los datos de ciencia ficción es inmediatamente evidente: podemos ver fácilmente la estructura general de los datos: Australia se compone de seis estados y algunos territorios. Hay 9 unidades geográficas distintas, por lo que hay 9 filas en este tibble (cf. mi_counties data donde hay una fila por vértice del polígono).

La columna más importante es “geometría” geometry, que especifica la geometría espacial para cada uno de los estados y territorios. Cada elemento de la columna geometry es un objeto multipolígono que, como su nombre indica, contiene datos que especifican los vértices de uno o más polígonos que delimitan el borde de una región. Dados los datos en este formato, podemos usar geom_sf() y coord_sf() para dibujar un mapa útil sin especificar ningún parámetro o incluso declarar explícitamente ninguna estética:

ggplot(oz_states) + 
  geom_sf() + 
  coord_sf()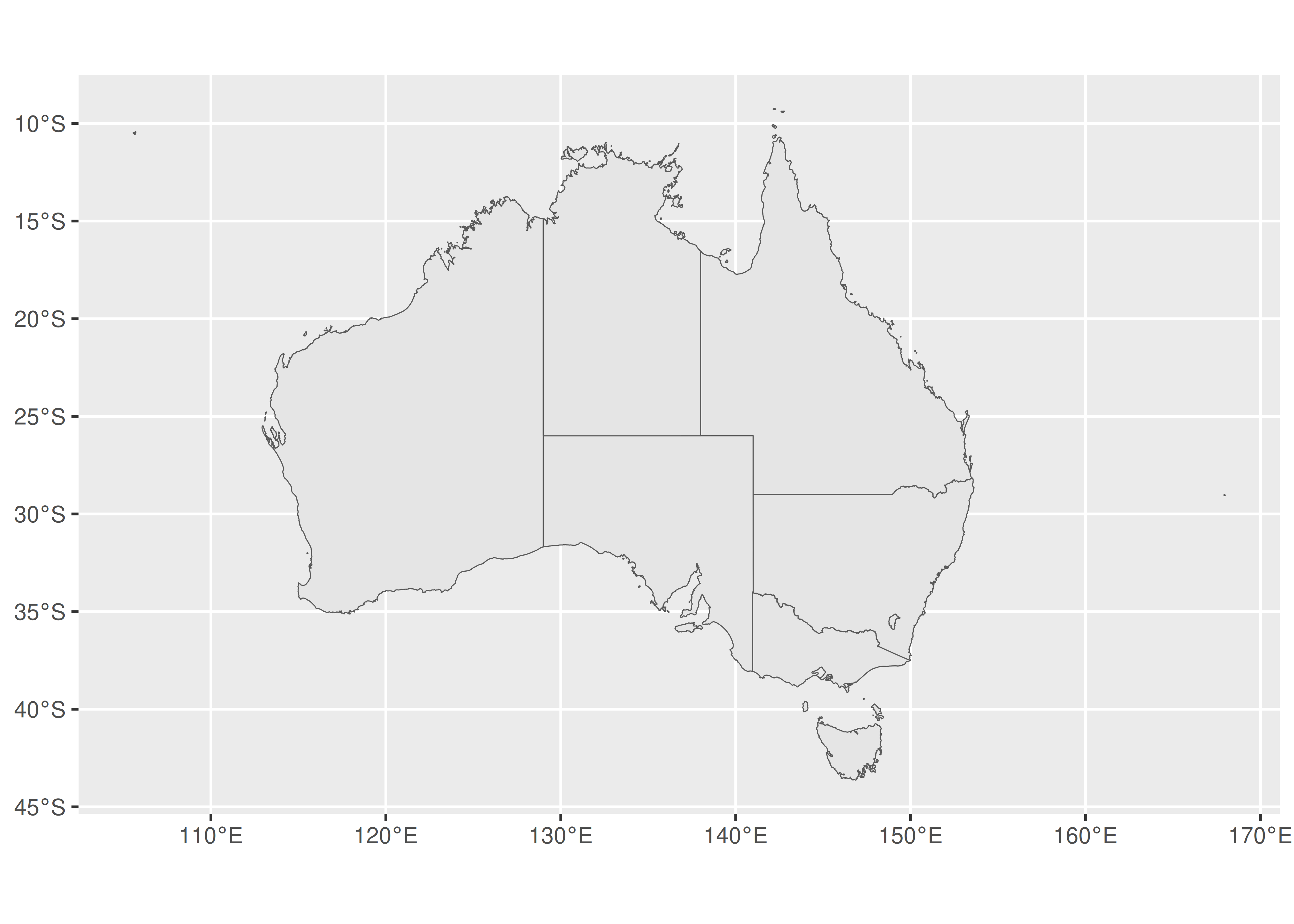

Para entender por qué esto funciona, tenga en cuenta que geom_sf() se basa en una estética de geometry que no se utiliza en ninguna otra parte de ggplot2. Esta estética se puede especificar de una de tres maneras:

  • En el caso más simple (ilustrado arriba) cuando el usuario no hace nada, geom_sf() intentará asignarlo a una columna llamada geometry.

  • Si el argumento data es un objeto sf entonces geom_sf() puede detectar automáticamente una columna de geometría, incluso si no se llama geometry.

  • Puede especificar el mapeo manualmente de la forma habitual con aes(geometry = my_column). Esto es útil si tiene varias columnas de geometría.

La función coord_sf() gobierna la proyección del mapa, discutida en Sección 6.3.

6.2.1 Mapas en capas

En algunos casos, es posible que desees superponer un mapa encima de otro. El paquete ggplot2 admite esto permitiéndole agregar múltiples capas geom_sf() a un gráfico. Como ejemplo, usaremos los datos de “oz_states” para dibujar los estados australianos en diferentes colores y superpondremos este gráfico con los límites de las regiones electorales australianas. Para hacer esto, hay que realizar dos pasos de preprocesamiento. Primero, usaremos dplyr::filter() para eliminar los “Other Territories” de las fronteras estatales.

El siguiente código dibuja un gráfico con dos capas de mapa: la primera usa oz_states para llenar los estados en diferentes colores, y la segunda usa oz_votes para dibujar los límites electorales. En segundo lugar, extraeremos los límites electorales de forma simplificada utilizando la función ms_simplify() del paquete rmapshaper (Teucher y Russell 2018). Generalmente, esto es una buena idea si el conjunto de datos original (en este caso, ozmaps::abs_ced) se almacena a una resolución más alta que la que requiere su gráfico, para reducir el tiempo necesario para renderizar el gráfico.

oz_states <- ozmaps::ozmap_states %>% filter(NAME != "Other Territories")
oz_votes <- rmapshaper::ms_simplify(ozmaps::abs_ced)

Ahora que tenemos los conjuntos de datos oz_states y oz_votes para representar las fronteras estatales y electorales respectivamente, el gráfico deseado se puede construir agregando dos capas geom_sf() al gráfico:

ggplot() + 
  geom_sf(data = oz_states, mapping = aes(fill = NAME), show.legend = FALSE) +
  geom_sf(data = oz_votes, fill = NA) + 
  coord_sf()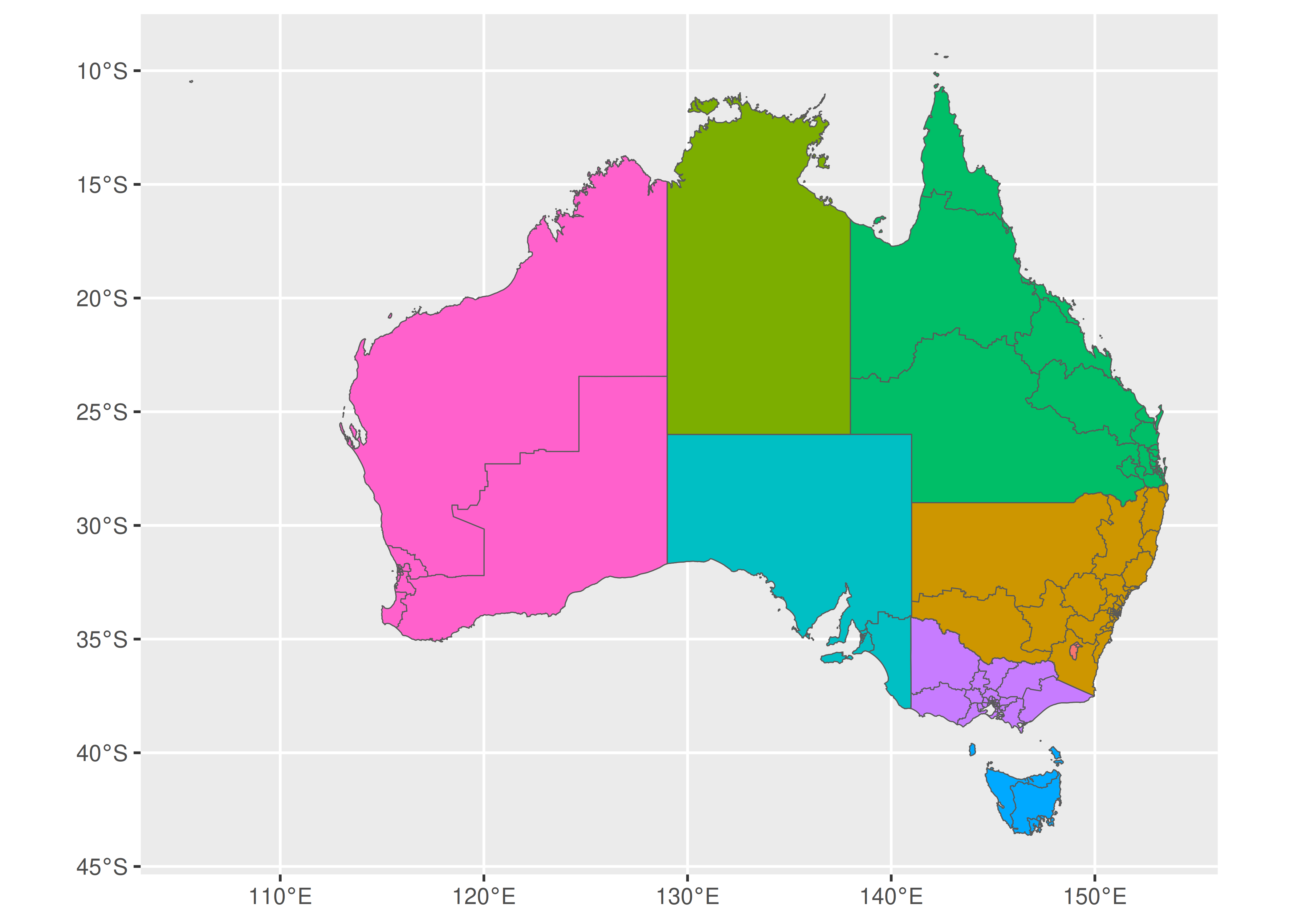

Vale la pena señalar que la primera capa de este gráfico asigna la estética del fill a una variable de los datos. En este caso, la variable NAME es una variable categórica y no transmite ninguna información adicional, pero se puede utilizar el mismo enfoque para visualizar otros tipos de metadatos de área. Por ejemplo, si oz_states tuviera una columna adicional que especificara el nivel de desempleo en cada estado, podríamos asignar la estética del fill a esa variable.

6.2.2 Mapas etiquetados

Agregar etiquetas a mapas es un ejemplo de anotar gráficos (Capítulo 8) y es compatible con geom_sf_label() y geom_sf_text(). Por ejemplo, si bien es razonable esperar que una audiencia australiana conozca los nombres de los estados australianos (y no están etiquetados en el gráfico anterior), pocos australianos conocerían los nombres de los diferentes electorados en la región metropolitana de Sydney. Entonces, para dibujar un mapa electoral de Sydney, primero necesitaríamos extraer los datos del mapa para los electorados relevantes y luego agregar la etiqueta. El siguiente gráfico se acerca a la región de Sydney especificando xlim y ylim en coord_sf() y luego usa geom_sf_label() para superponer cada electorado con una etiqueta:

# Filtrar electorados en la región metropolitana de Sydney
sydney_map <- ozmaps::abs_ced %>% filter(NAME %in% c(
  "Sydney", "Wentworth", "Warringah", "Kingsford Smith", "Grayndler", "Lowe", 
  "North Sydney", "Barton", "Bradfield", "Banks", "Blaxland", "Reid", 
  "Watson", "Fowler", "Werriwa", "Prospect", "Parramatta", "Bennelong", 
  "Mackellar", "Greenway", "Mitchell", "Chifley", "McMahon"
))

# Dibuja el mapa electoral de Sydney
ggplot(sydney_map) + 
  geom_sf(aes(fill = NAME), show.legend = FALSE) + 
  coord_sf(xlim = c(150.97, 151.3), ylim = c(-33.98, -33.79)) + 
  geom_sf_label(aes(label = NAME), label.padding = unit(1, "mm"))
#> Warning in st_point_on_surface.sfc(sf::st_zm(x)): st_point_on_surface may not
#> give correct results for longitude/latitude data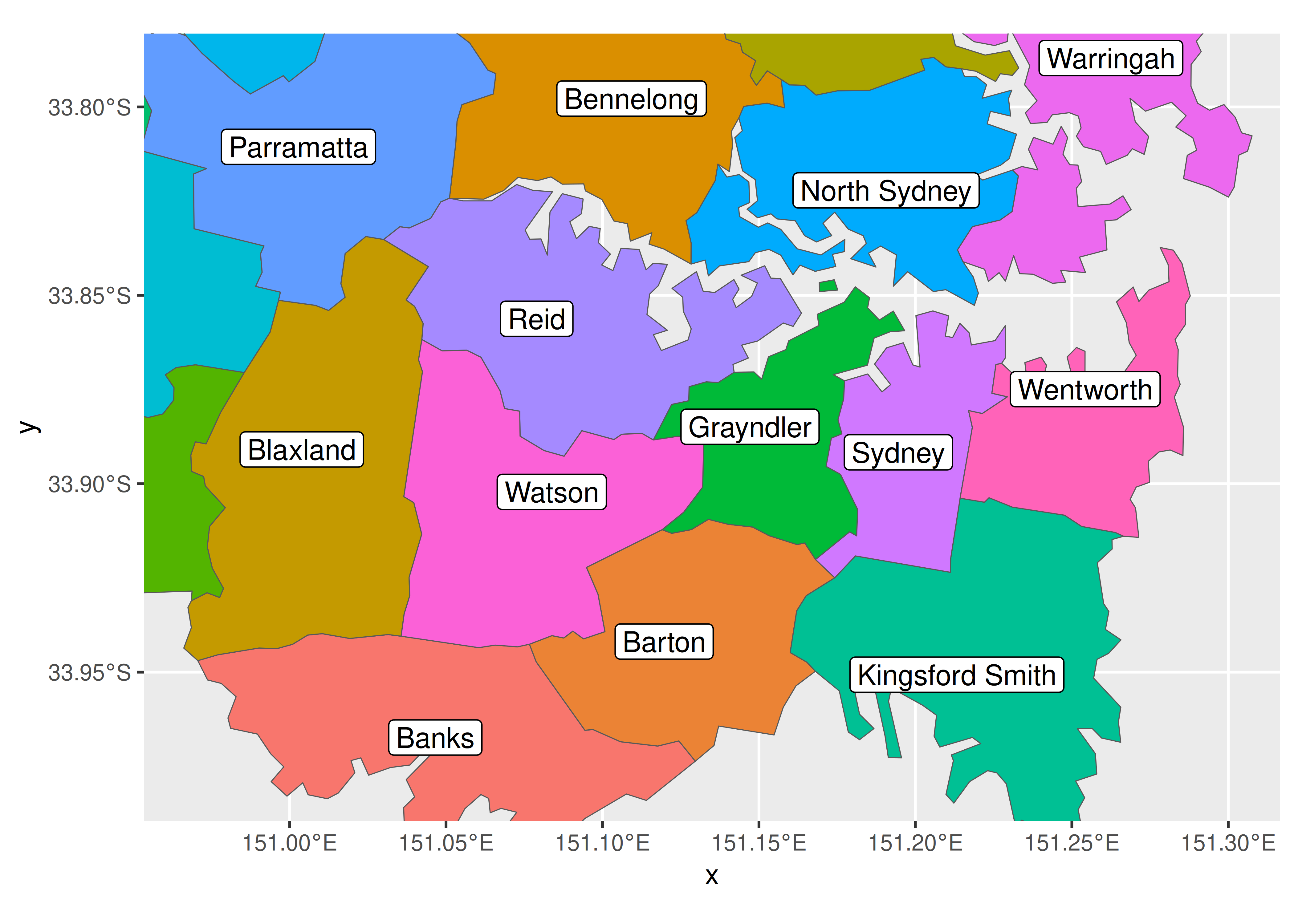

Vale la pena señalar el mensaje de advertencia. Internamente, geom_sf_label() usa la función st_point_on_surface() del paquete sf para colocar etiquetas, y el mensaje de advertencia aparece porque la mayoría de los algoritmos utilizados por sf para calcular cantidades geométricas (por ejemplo, centroides, puntos interiores) se basan en una suposición. que los puntos se encuentran sobre una superficie plana bidimensional y parametrizados con coordenadas cartesianas. Esta suposición no está estrictamente justificada y, en algunos casos (por ejemplo, regiones cercanas a los polos), los cálculos que tratan la longitud y la latitud de esta manera darán respuestas erróneas. Por este motivo, el paquete sf genera mensajes de advertencia cuando se basa en esta aproximación.

6.2.3 Agregar otras geomas

Aunque geom_sf() es especial en algunos aspectos, se comporta de la misma manera que cualquier otra geom, lo que permite trazar datos adicionales en un mapa con geoms estándar. Por ejemplo, es posible que deseemos trazar las ubicaciones de las capitales australianas en el mapa usando geom_point(). El siguiente código ilustra cómo se hace esto:

oz_capitals <- tibble::tribble( 
  ~city,           ~lat,     ~lon,
  "Sydney",    -33.8688, 151.2093,  
  "Melbourne", -37.8136, 144.9631, 
  "Brisbane",  -27.4698, 153.0251, 
  "Adelaide",  -34.9285, 138.6007, 
  "Perth",     -31.9505, 115.8605, 
  "Hobart",    -42.8821, 147.3272, 
  "Canberra",  -35.2809, 149.1300, 
  "Darwin",    -12.4634, 130.8456, 
)

ggplot() + 
  geom_sf(data = oz_votes) + 
  geom_sf(data = oz_states, colour = "black", fill = NA) + 
  geom_point(data = oz_capitals, mapping = aes(x = lon, y = lat), colour = "red") + 
  coord_sf()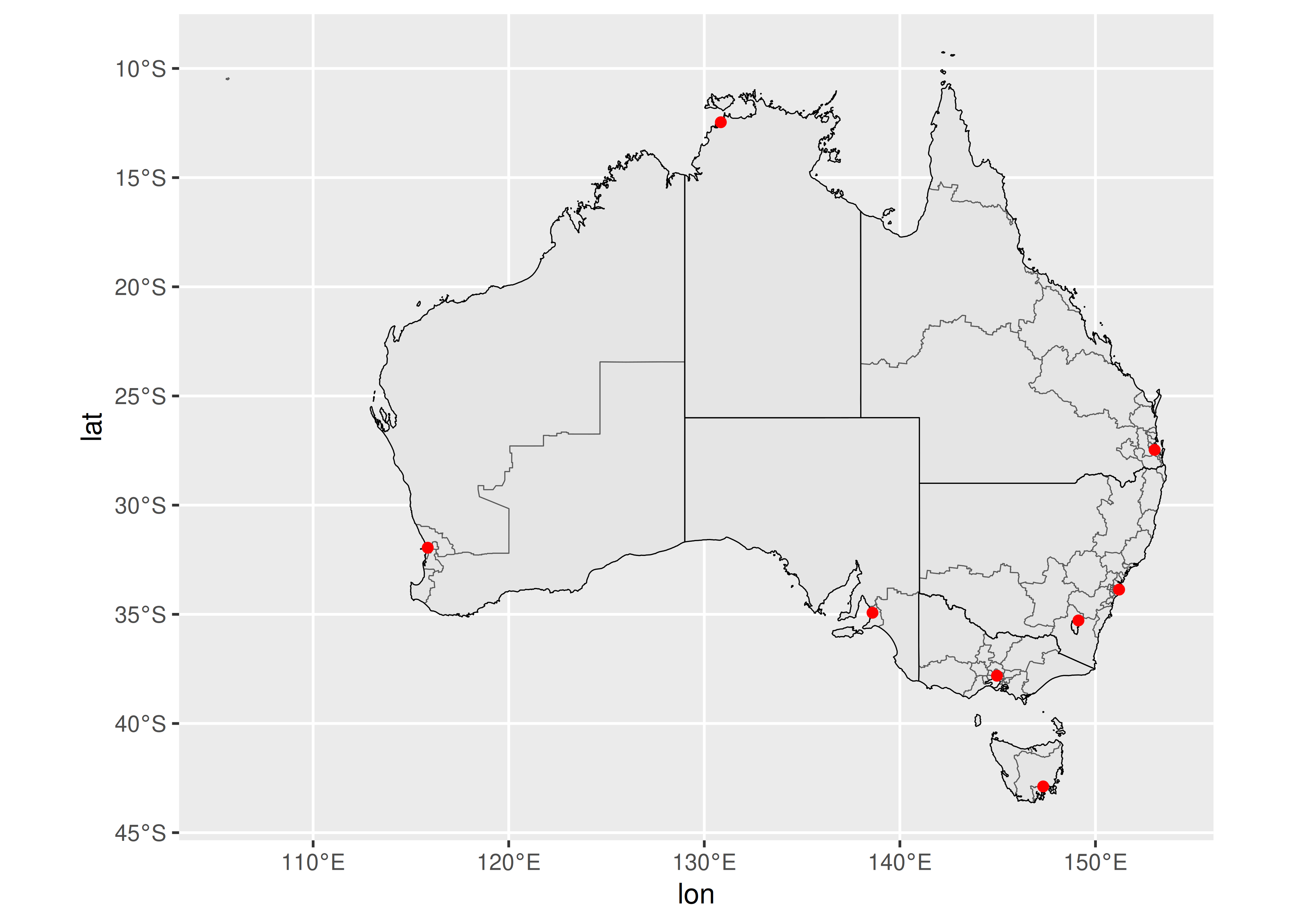

En este ejemplo, geom_point se usa solo para especificar las ubicaciones de las ciudades capitales, pero la idea básica se puede ampliar para manejar metadatos de puntos de manera más general. Por ejemplo, si los datos de oz_capitals incluyeran una variable adicional que especificara el número de electorados dentro de cada área metropolitana, podríamos codificar esos datos utilizando la estética size.

6.3 Proyecciones de mapas

Al comienzo del capítulo dibujamos mapas trazando la longitud y la latitud en un plano cartesiano, como si los datos geoespaciales no fueran diferentes de otros tipos de datos que uno podría querer trazar. En una primera aproximación, esto está bien, pero no es lo suficientemente bueno si lo que importa es la precisión. Hay dos problemas fundamentales con este enfoque.

La primera cuestión es la forma del planeta. La Tierra no es un plano ni una esfera perfecta. Como consecuencia, para asignar un valor de coordenadas (longitud y latitud) a una ubicación necesitamos hacer suposiciones sobre todo tipo de cosas. ¿Qué tan elipsoidal es la Tierra? ¿Dónde está el centro del planeta? ¿Dónde está el punto de origen de la longitud y la latitud? ¿Dónde está el nivel del mar? ¿Cómo se mueven las placas tectónicas? Todas estas cosas son relevantes y, dependiendo de las suposiciones que se hagan, la misma coordenada se puede asignar a ubicaciones que están a muchos metros de distancia. El conjunto de suposiciones sobre la forma de la Tierra se conoce como dato geodésico y, si bien puede no ser importante para algunas visualizaciones de datos, para otras es fundamental. Hay varias opciones diferentes que uno podría considerar: si su enfoque es América del Norte, el “Datum de América del Norte” (NAD83) es una buena opción, mientras que si su perspectiva es global, el “Sistema Geodésico Mundial” (WGS84) probablemente sea mejor.

La segunda cuestión es la forma de su mapa. La Tierra es aproximadamente elipsoidal, pero en la mayoría de los casos los datos espaciales deben dibujarse en un plano bidimensional. No es posible mapear la superficie de un elipsoide en un plano sin cierta distorsión o corte, y tendrás que elegir qué distorsiones estás dispuesto a aceptar al dibujar un mapa. Este es el trabajo de la proyección cartográfica.

Las proyecciones cartográficas a menudo se clasifican en términos de las propiedades geométricas que conservan, p.

  • Las proyecciones que preservan el área garantizan que las regiones de igual área en el mundo se dibujen con igual área en el mapa.

  • Las proyecciones que preservan la forma (o conformes) garantizan que se conserve la forma local de las regiones.

Y desafortunadamente, no es posible que ninguna proyección conserve la forma y el área. Esto hace que esté un poco más allá del alcance de este libro discutir las proyecciones cartográficas en detalle, aparte de señalar que la especificación de características simples le permite indicar qué proyección cartográfica desea utilizar. Para obtener más información sobre proyecciones de mapas, consulte Geocómputo con R https://geocompr.robinlovelace.net/ (Lovelace, Nowosad, y Muenchow 2019).

En conjunto, el datum geodésico (p. ej., WGS84), el tipo de proyección cartográfica (p. ej., Mercator) y los parámetros de la proyección (p. ej., ubicación del origen) especifican un sistema de referencia de coordenadas, o CRS, un conjunto completo de suposiciones utilizadas para traducir la información de latitud y longitud en un mapa bidimensional. Un objeto sf a menudo incluye un CRS predeterminado, como se ilustra a continuación:

st_crs(oz_votes)
#> Coordinate Reference System:
#>   User input: EPSG:4283 
#>   wkt:
#> GEOGCRS["GDA94",
#>     DATUM["Geocentric Datum of Australia 1994",
#>         ELLIPSOID["GRS 1980",6378137,298.257222101,
#>             LENGTHUNIT["metre",1]]],
#>     PRIMEM["Greenwich",0,
#>         ANGLEUNIT["degree",0.0174532925199433]],
#>     CS[ellipsoidal,2],
#>         AXIS["geodetic latitude (Lat)",north,
#>             ORDER[1],
#>             ANGLEUNIT["degree",0.0174532925199433]],
#>         AXIS["geodetic longitude (Lon)",east,
#>             ORDER[2],
#>             ANGLEUNIT["degree",0.0174532925199433]],
#>     USAGE[
#>         SCOPE["Horizontal component of 3D system."],
#>         AREA["Australia including Lord Howe Island, Macquarie Islands, Ashmore and Cartier Islands, Christmas Island, Cocos (Keeling) Islands, Norfolk Island. All onshore and offshore."],
#>         BBOX[-60.56,93.41,-8.47,173.35]],
#>     ID["EPSG",4283]]

La mayor parte de este resultado corresponde a una cadena de texto conocido (WKT) que describe sin ambigüedades el CRS. sf utiliza esta representación detallada de WKT internamente, pero hay varias formas de proporcionar información al usuario que sf comprenda. Uno de esos métodos es proporcionar entrada numérica en forma de código EPSG (consulte https://epsg.org/home.html). El CRS predeterminado en los datos oz_votes corresponde al código EPSG 4283: El CRS predeterminado en los datos oz_votes corresponde al código EPSG 4283:

st_crs(oz_votes) == st_crs(4283)
#> [1] TRUE

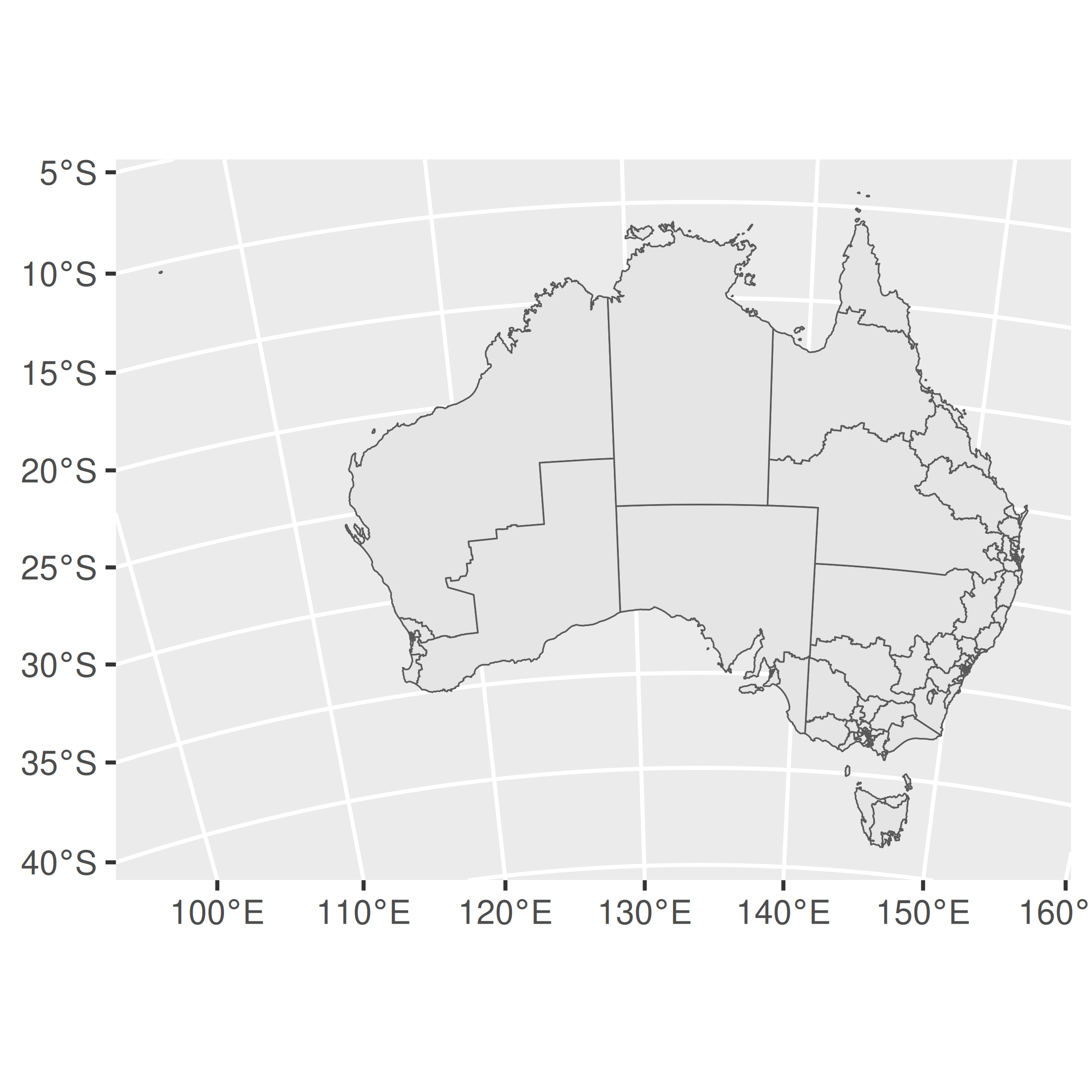
En ggplot2, el CRS está controlado por coord_sf(), lo que garantiza que cada capa del gráfico utilice la misma proyección. Por defecto, coord_sf() usa el CRS asociado con la columna de geometría de los datos1. Dado que los datos de ciencia ficción suelen ofrecer una opción sensata de CRS, este proceso normalmente se desarrolla de forma invisible y no requiere intervención del usuario. Sin embargo, si necesita configurar el CRS usted mismo, puede especificar el parámetro crs pasando una entrada de usuario válida a st_crs(). El siguiente ejemplo ilustra cómo cambiar del CRS predeterminado al código EPSG 3112:

ggplot(oz_votes) + geom_sf()
ggplot(oz_votes) + geom_sf() + coord_sf(crs = st_crs(3112))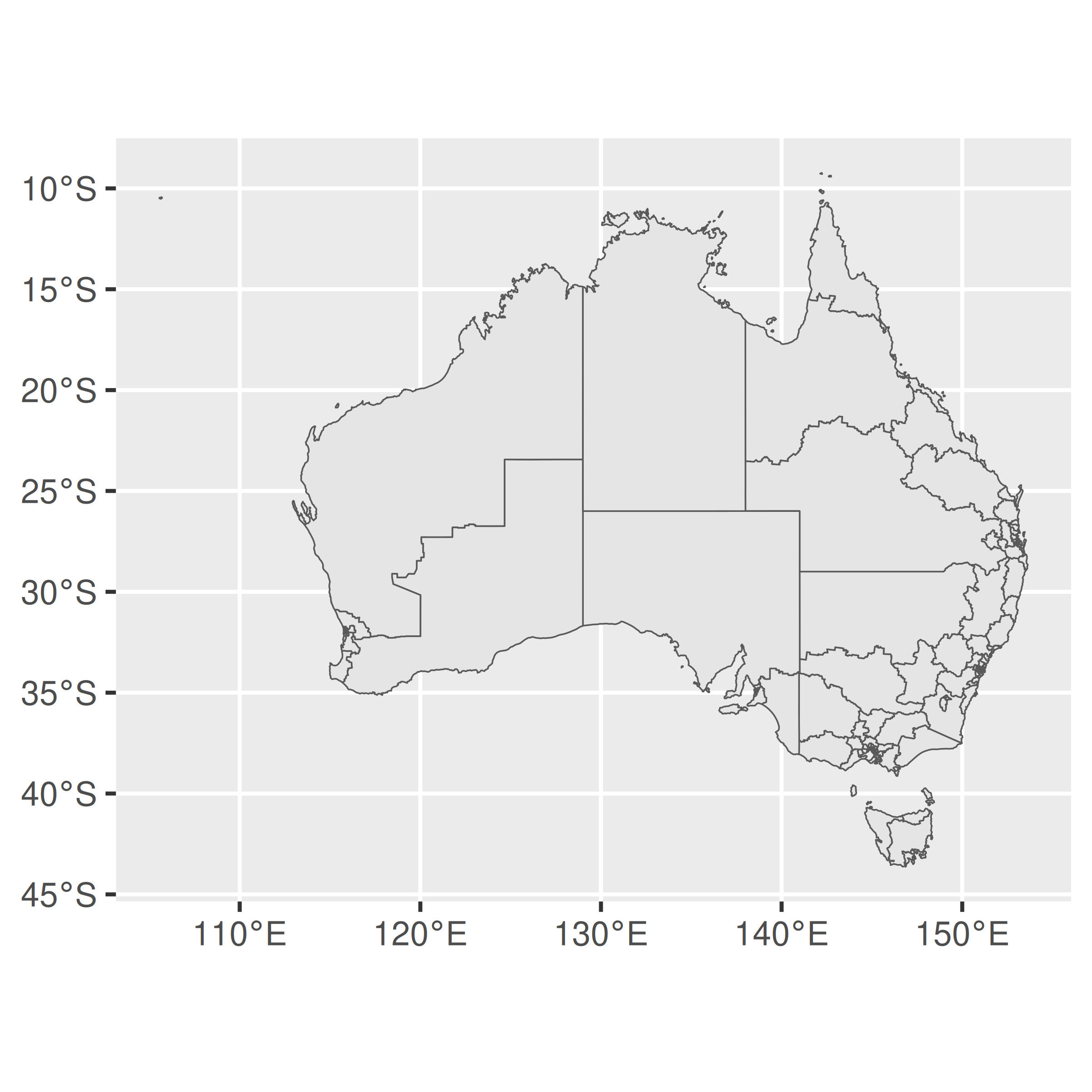

6.4 Trabajar con datos sf

Como se señaló anteriormente, los mapas creados usando geom_sf() y coord_sf() dependen en gran medida de las herramientas proporcionadas por el paquete sf y, de hecho, el paquete sf contiene muchas más herramientas útiles para manipular datos de características simples. En esta sección proporcionamos una introducción a algunas de estas herramientas; Puede encontrar una cobertura más detallada en el sitio web del paquete SF https://r-spatial.github.io/sf/.

Para comenzar, recuerde que una ventaja de las características simples sobre otras representaciones de datos espaciales es que las unidades geográficas pueden tener una estructura complicada. Un buen ejemplo de esto en los datos de los mapas australianos es el distrito electoral de Eden-Monaro, que se muestra a continuación:

edenmonaro <- ozmaps::abs_ced %>% filter(NAME == "Eden-Monaro")

p <- ggplot(edenmonaro) + geom_sf()
p + coord_sf(xlim = c(147.75, 150.25), ylim = c(-37.5, -34.5)) 
p + coord_sf(xlim = c(150, 150.25), ylim = c(-36.3, -36))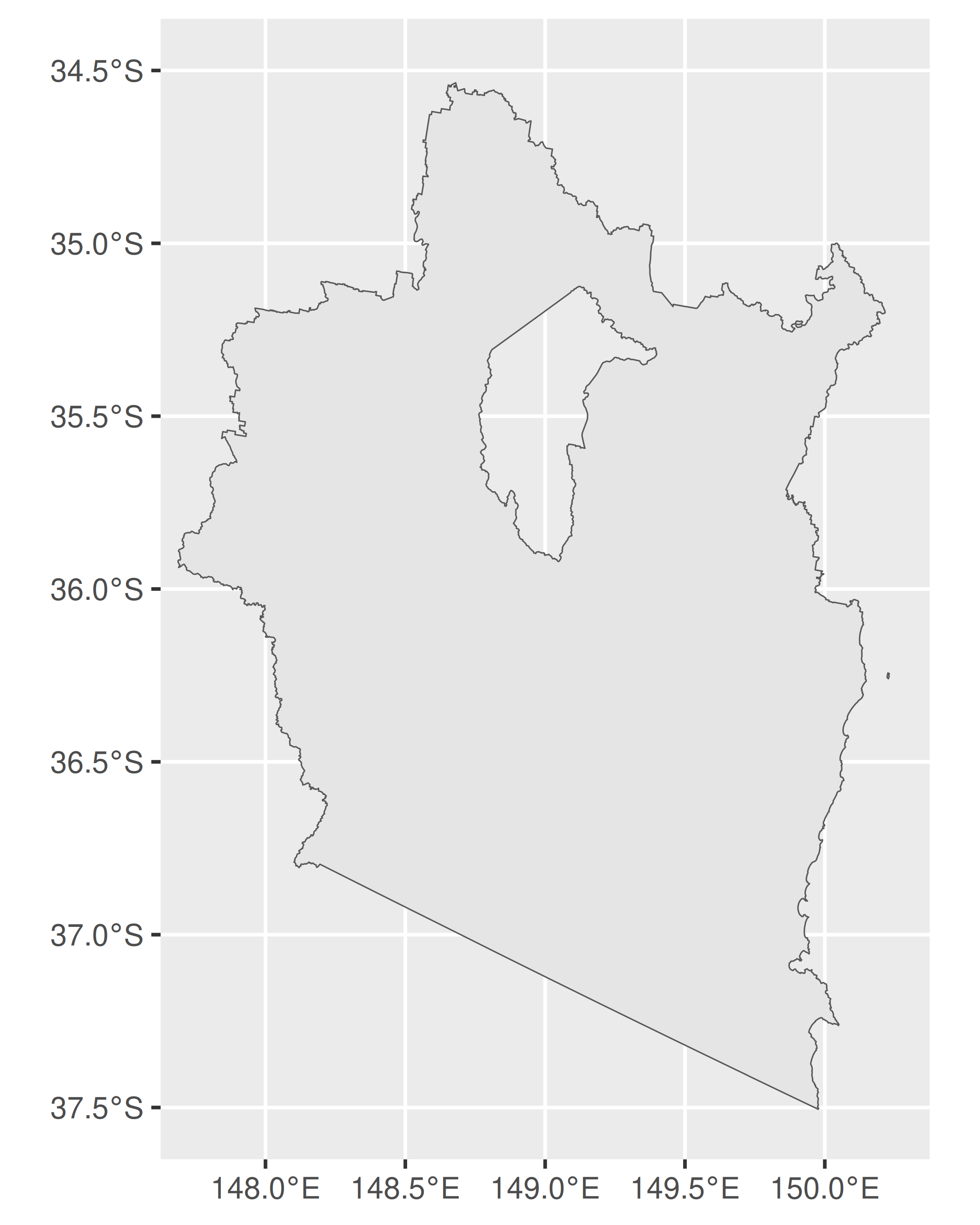

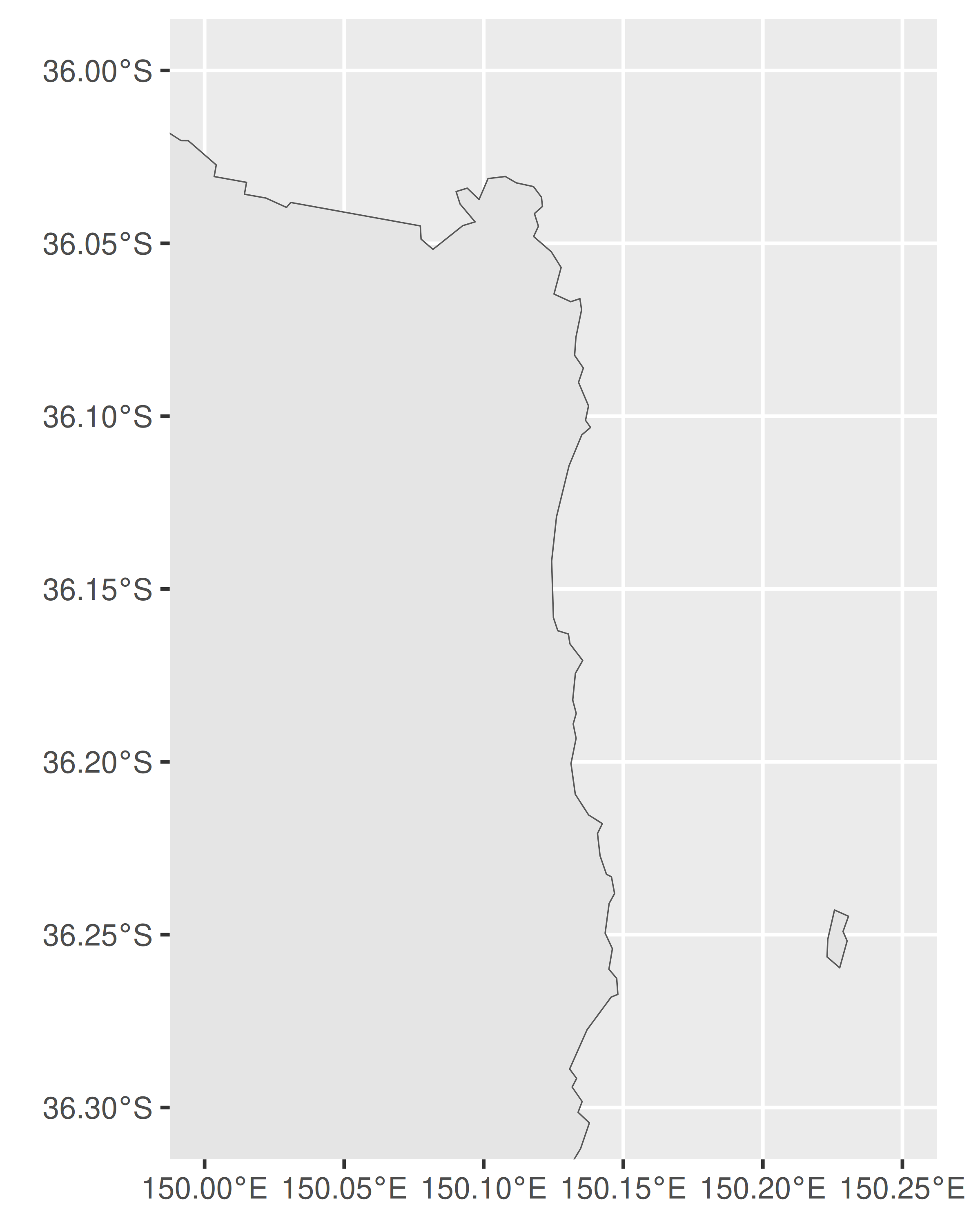
Como lo ilustra esto, Eden-Monaro se define en términos de dos polígonos distintos, uno grande en el continente australiano y una isla pequeña. Sin embargo, la gran región tiene un agujero en el medio (el agujero existe porque el Territorio de la Capital Australiana es una unidad política distinta que está totalmente contenida dentro de Eden-Monaro y, como se ilustra arriba, las fronteras electorales en Australia no cruzan las fronteras estatales). En terminología sf, este es un ejemplo de geometría MULTIPOLYGON. En esta sección hablaremos sobre la estructura de estos objetos y cómo trabajar con ellos.

Primero, usemos dplyr para tomar solo el objeto de geometría:

edenmonaro <- edenmonaro %>% pull(geometry)

Se puede acceder a los metadatos del objeto edenmonaro mediante funciones auxiliares. Por ejemplo, st_geometry_type() extrae el tipo de geometría (por ejemplo, MULTIPOLYGON), st_dimension() extrae el número de dimensiones (2 para datos XY, 3 para XYZ), st_bbox() extrae el cuadro delimitador como un vector numérico, y st_crs() extrae el CRS como una lista con dos componentes, uno para el código EPSG y el otro para proj4string. Por ejemplo:

st_bbox(edenmonaro)
#>  xmin  ymin  xmax  ymax 
#> 147.7 -37.5 150.2 -34.5

Normalmente, cuando imprimimos el objeto edenmonaro, la salida mostrará toda la información adicional (dimensión, cuadro delimitador, dato geodésico, etc.), pero durante el resto de esta sección mostraremos solo las líneas relevantes de la salida. En este caso, edenmonaro está definido por una geometría MULTIPOLYGON que contiene una característica:

edenmonaro 
#> Geometry set for 1 feature 
#> Geometry type: MULTIPOLYGON
#> MULTIPOLYGON (((150 -36.2, 150 -36.2, 150 -36.3...

Sin embargo, podemos “fundir” el MULTIPOLYGON en las dos geometrías POLYGON distintas a partir de las cuales está construido usando st_cast():

st_cast(edenmonaro, "POLYGON")
#> Geometry set for 2 features 
#> Geometry type: POLYGON
#> POLYGON ((150 -36.2, 150 -36.2, 150 -36.3, 150 ...
#> POLYGON ((148 -36.7, 148 -36.7, 148 -36.7, 148 ...

Para ilustrar cuándo esto podría ser útil, consideremos el electorado de Dawson, que consta de 69 islas además de una región costera en el continente australiano.

dawson <- ozmaps::abs_ced %>% 
  filter(NAME == "Dawson") %>% 
  pull(geometry)
dawson
#> Geometry set for 1 feature 
#> Geometry type: MULTIPOLYGON
#> MULTIPOLYGON (((148 -19.9, 148 -19.8, 148 -19.8...

ggplot(dawson) + 
  geom_sf() +
  coord_sf()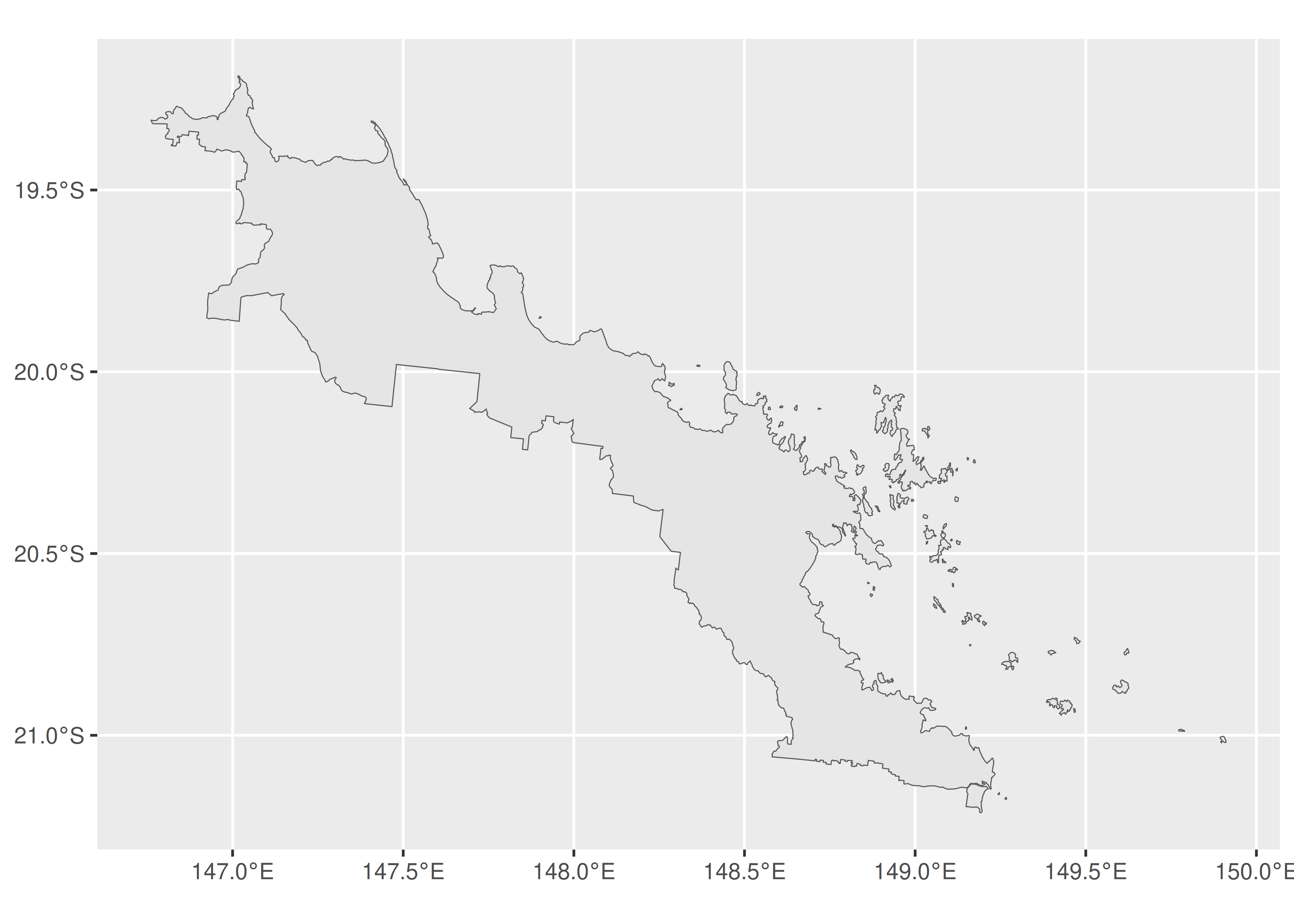

Supongamos, sin embargo, que nuestro interés es sólo cartografiar las islas. Si es así, primero podemos usar la función st_cast() para dividir el electorado de Dawson en los polígonos constituyentes. Después de hacerlo, podemos usar st_area() para calcular el área de cada polígono y which.max() para encontrar el polígono con área máxima:

dawson <- st_cast(dawson, "POLYGON")
which.max(st_area(dawson))
#> [1] 69

La gran región continental corresponde al polígono 69 dentro de Dawson. Armados con este conocimiento, podemos dibujar un mapa que muestre solo las islas:

ggplot(dawson[-69]) + 
  geom_sf() + 
  coord_sf()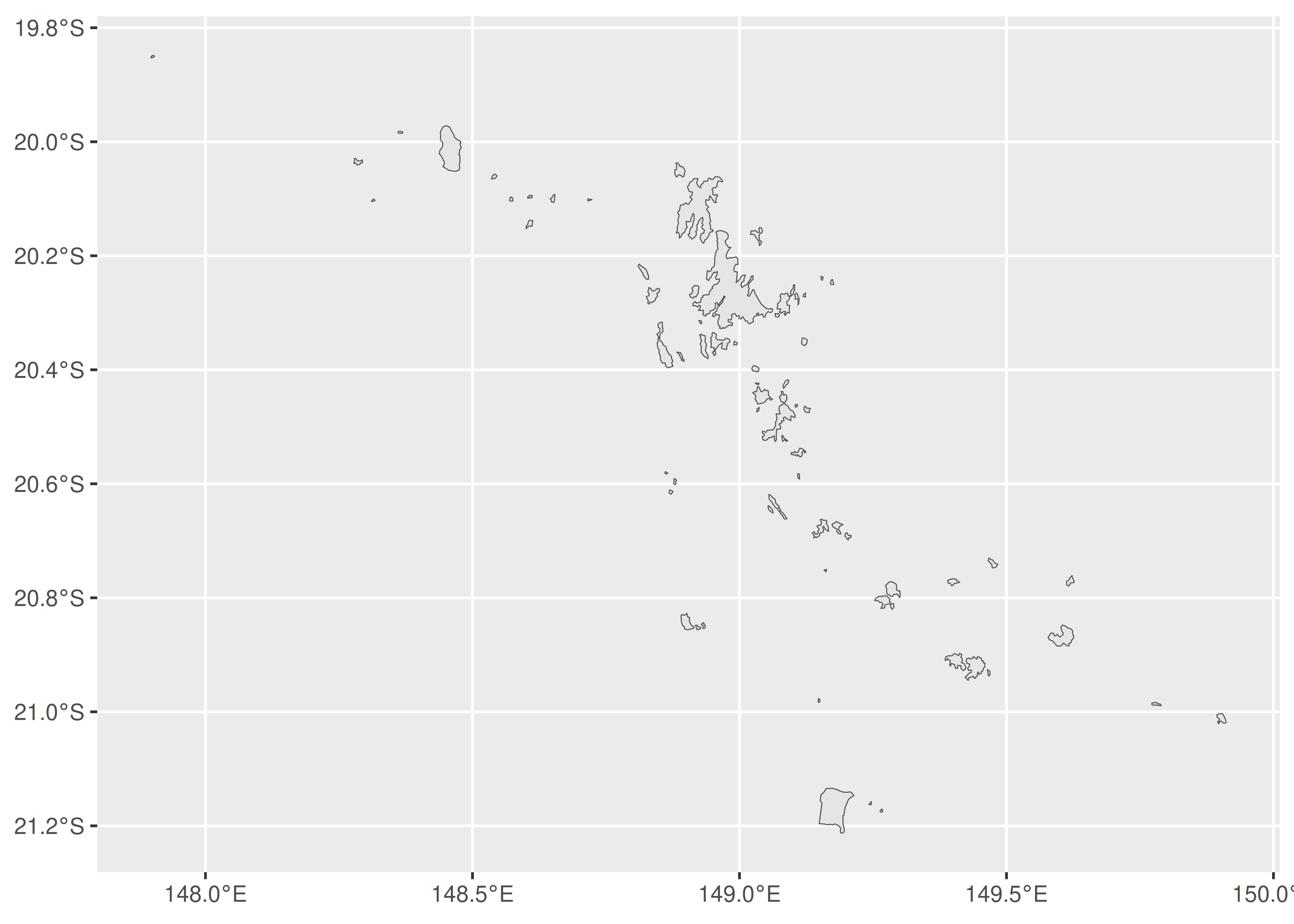

6.5 Mapas ráster

Una segunda forma de proporcionar información geoespacial para la cartografía es confiar en datos ráster. A diferencia del formato de entidades simples, en el que las entidades geográficas se especifican en términos de un conjunto de líneas, puntos y polígonos, los rásteres toman la forma de imágenes. En el caso más simple, los datos ráster pueden no ser más que un archivo de mapa de bits, pero existen muchos formatos de imagen diferentes. Específicamente en el contexto geoespacial, existen formatos de imágenes que incluyen metadatos (por ejemplo, datos geodésicos, sistema de referencia de coordenadas) que se pueden usar para mapear la información de la imagen en la superficie de la Tierra. Por ejemplo, un formato común es GeoTIFF, que es un archivo TIFF normal con metadatos adicionales. Afortunadamente, la mayoría de los formatos se pueden leer fácilmente en R con la ayuda de GDAL (la Biblioteca de abstracción de datos geoespaciales, https://gdal.org/). Por ejemplo, el paquete sf contiene una función sf::gdal_read() que proporciona acceso a los controladores ráster GDAL desde R. Sin embargo, rara vez es necesario llamar a esta función directamente, ya que existen otras funciones de alto nivel que se encargan de esto. para ti.

Como ilustración, usaremos una imagen de satélite tomada por el satélite geoestacionario Himawari-8 operado por la Agencia Meteorológica de Japón y obtenida originalmente del sitio web de la Oficina Australiana de Meteorología. Esta imagen está almacenada en un archivo GeoTIFF llamado “IDE00422.202001072100.tif”.2 Para importar estos datos a R, usaremos el paquete de estrellas (Pebesma 2020) para crear objetos de estrellas:

library(stars)
#> Loading required package: abind
sat_vis <- read_stars(
  "IDE00422.202001072100.tif", 
  RasterIO = list(nBufXSize = 600, nBufYSize = 600)
)

En el código anterior, el primer argumento especifica la ruta al archivo ráster y el argumento RasterIO se usa para pasar una lista de parámetros de bajo nivel a GDAL. En este caso, hemos utilizado nBufXSize y nBufYSize para garantizar que R lea los datos en baja resolución (como una imagen de 600x600 píxeles). Para ver qué información ha importado R, podemos inspeccionar el objeto sat_vis:

sat_vis
#> stars object with 3 dimensions and 1 attribute
#> attribute(s), summary of first 1e+05 cells:
#>                            Min. 1st Qu. Median Mean 3rd Qu. Max.
#> IDE00422.202001072100.tif     0       0      0 18.1       0  255
#> dimension(s):
#>      from  to   offset  delta                  refsys point x/y
#> x       1 600 -5500000  18333 Geostationary_Satellite FALSE [x]
#> y       1 600  5500000 -18333 Geostationary_Satellite FALSE [y]
#> band    1   3       NA     NA                      NA    NA

Este resultado nos dice algo sobre la estructura de un objeto estrella. Para el objeto sat_vis, los datos subyacentes se almacenan como una matriz tridimensional, con las dimensiones x e y que especifican los datos espaciales. La dimensión band en este caso corresponde al canal de color (RGB), pero es redundante para esta imagen ya que los datos están en escala de grises. En otros conjuntos de datos puede haber bandas correspondientes a diferentes sensores y posiblemente también una dimensión temporal. Tenga en cuenta que los datos espaciales también están asociados con un sistema de referencia de coordenadas (denominado “refsys” en el resultado).

Para trazar los datos sat_vis en ggplot2, podemos usar la función geom_stars() proporcionada por el paquete stars. Un gráfico mínimo podría verse así:

ggplot() + 
  geom_stars(data = sat_vis) + 
  coord_equal()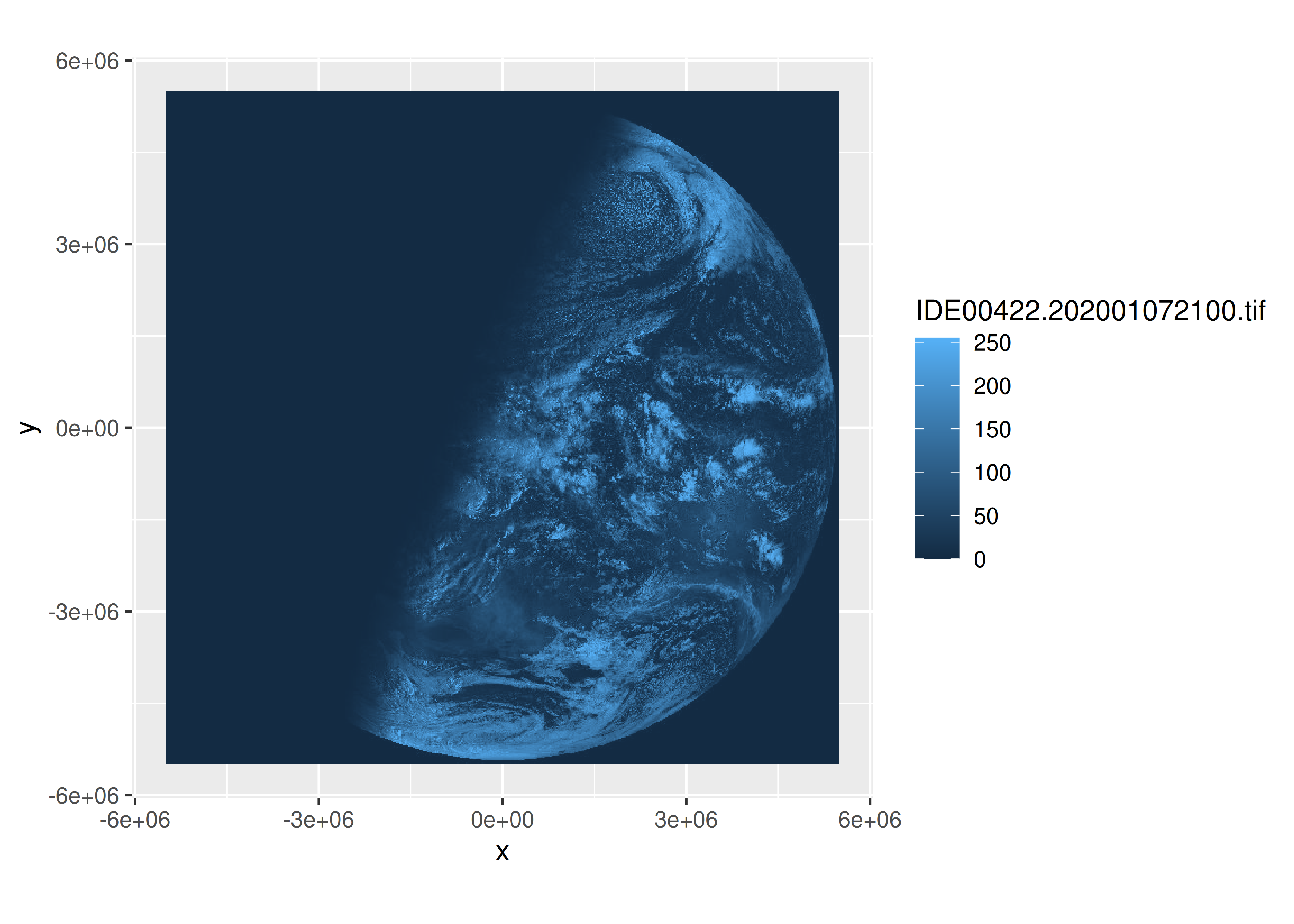

La función geom_stars() requiere que el argumento data sea un objeto de estrellas y asigna los datos ráster a la estética de relleno. En consecuencia, el sombreado azul en la imagen de satélite de arriba está determinado por la escala ggplot2, no por la imagen en sí. Es decir, aunque sat_vis contiene tres bandas, el gráfico anterior solo muestra la primera, y los valores de datos sin procesar (que van de 0 a 255) se asignan a la paleta azul predeterminada que usa ggplot2 para datos continuos. Para ver cómo se ve “realmente” el archivo de imagen, podemos separar las bandas usando facet_wrap():

ggplot() + 
  geom_stars(data = sat_vis, show.legend = FALSE) +
  facet_wrap(vars(band)) + 
  coord_equal() + 
  scale_fill_gradient(low = "black", high = "white")

Una limitación para mostrar solo la imagen sin procesar es que no es fácil determinar dónde están las masas de tierra relevantes y es posible que deseemos superponer los datos satelitales con el mapa vectorial oz_states para mostrar los contornos de las entidades políticas australianas. Sin embargo, se requiere cierto cuidado al hacerlo porque las dos fuentes de datos están asociadas con diferentes sistemas de referencia de coordenadas. Para proyectar los datos oz_states correctamente, los datos deben transformarse usando la función st_transform() del paquete sf. En el código siguiente, extraemos el CRS del objeto ráster sat_vis y transformamos los datos oz_states para usar el mismo sistema.

oz_states <- st_transform(oz_states, crs = st_crs(sat_vis))

Una vez hecho esto, ahora podemos dibujar el mapa vectorial sobre la parte superior de la imagen rasterizada para que la imagen sea más interpretable para el lector. Ahora se desprende claramente de la inspección que la imagen de satélite fue tomada durante el amanecer en Australia:

ggplot() + 
  geom_stars(data = sat_vis, show.legend = FALSE) +
  geom_sf(data = oz_states, fill = NA, color = "white") + 
  coord_sf() + 
  theme_void() + 
  scale_fill_gradient(low = "black", high = "white")

¿Qué pasaría si quisiéramos trazar datos más convencionales en la parte superior? Un ejemplo sencillo de esto sería trazar las ubicaciones de las capitales australianas según el marco de datos oz_capitals que contiene datos de latitud y longitud. Sin embargo, debido a que estos datos no están asociados con un CRS y no están en la misma escala que los datos ráster en sat_vis, también deberán transformarse. Para hacerlo, primero necesitamos crear un objeto sf a partir de los datos de oz_capitals usando st_as_sf():

cities <- oz_capitals %>% 
  st_as_sf(coords = c("lon", "lat"), crs = 4326, remove = FALSE)

Esta proyección se establece utilizando el código EPSG 4326, una proyección elipsoidal que utiliza los valores de latitud y longitud como coordenadas y se basa en el datum WGS84. Una vez hecho esto, ahora podemos transformar las coordenadas de la geometría de latitud-longitud para que coincidan con la geometría de nuestros datos sat_vis:

cities <- st_transform(cities, st_crs(sat_vis))

Los datos transformados ahora se pueden superponer usando geom_sf():

ggplot() + 
  geom_stars(data = sat_vis, show.legend = FALSE) +
  geom_sf(data = oz_states, fill = NA, color = "white") + 
  geom_sf(data = cities, color = "red") + 
  coord_sf() + 
  theme_void() + 
  scale_fill_gradient(low = "black", high = "white")

Esta versión de la imagen deja más claro que la imagen de satélite fue tomada aproximadamente al amanecer en Darwin: el sol había salido en todas las ciudades del este, pero no en Perth. Esto podría aclararse en la visualización de datos usando la función geom_sf_text() para agregar etiquetas a cada ciudad. Por ejemplo, podríamos agregar otra capa al gráfico usando un código como este:

geom_sf_text(data = cities, mapping = aes(label = city))

aunque se requeriría algo de cuidado para asegurar que el texto esté bien colocado (ver Capítulo 8).

6.6 Fuentes de datos

  • El paquete de límites de EE.UU., https://github.com/ropensci/USAboundaries contiene datos de estado, condado y código postal de EE. UU. (Mullen y Bratt 2018). Además de los límites actuales, también tiene límites estatales y de condado que se remontan al siglo XVII.

  • El paquete tigris, https://github.com/walkerke/tigris, facilita el acceso a los archivos de forma TIGRIS del censo de EE. UU. (Walker 2019). Contiene límites de estados, condados, códigos postales y zonas censales, así como muchos otros conjuntos de datos útiles.

  • El paquete rnaturalearth (South 2017) reúne los datos gratuitos y de alta calidad de https://naturalearthdata.com/. Contiene las fronteras de los países y las fronteras de la región de nivel superior dentro de cada país (por ejemplo, estados de EE. UU., regiones de Francia, condados del Reino Unido).

  • El paquete osmar, https://cran.r-project.org/package=osmar resume la API de OpenStreetMap para que pueda acceder a una amplia gama de datos vectoriales, incluidas calles y edificios individuales (Eugster y Schlesinger 2010).

  • Si tienes tus propios archivos de formas (.shp) puedes cargarlos en R con sf::read_sf().

Eugster, Manuel J. A., y Thomas Schlesinger. 2010. «osmar: OpenStreetMap and R». R Journal. http://osmar.r-forge.r-project.org/RJpreprint.pdf.
Lovelace, Robin, Jakub Nowosad, y Jannes Muenchow. 2019. Geocomputation with R. CRC Press.
Mullen, Lincoln A., y Jordan Bratt. 2018. «USAboundaries: Historical and Contemporary Boundaries of the United States of America». Journal of Open Source Software 3: 314. https://doi.org/10.21105/joss.00314.
Pebesma, Edzer. 2018. «Simple Features for R: Standardized Support for Spatial Vector Data». The R Journal 10 (1): 439-46. https://doi.org/10.32614/RJ-2018-009.
———. 2020. stars: Spatiotemporal Arrays, Raster and Vector Data Cubes.
South, Andy. 2017. rnaturalearth: World Map Data from Natural Earth. https://CRAN.R-project.org/package=rnaturalearth.
Sumner, Michael. 2019. ozmaps: Australia Maps. https://CRAN.R-project.org/package=ozmaps.
Teucher, Andy, y Kenton Russell. 2018. rmapshaper: Client for ’mapshaper’ for ’Geospatial’ Operations. https://CRAN.R-project.org/package=rmapshaper.
Walker, Kyle. 2019. tigris: Load Census TIGER/Line Shapefiles. https://CRAN.R-project.org/package=tigris.

  1. Si hay varios conjuntos de datos con un CRS asociado diferente, utiliza el CRS de la primera capa.↩︎

  2. Si desea probar este código usted mismo, puede encontrar una copia de la imagen en el repositorio de GitHub del libro: https://github.com/hadley/ggplot2-book/raw/master/IDE00422.202001072100.tif.↩︎